“求其源，訴其真”：更“接地氣”的數學課堂

滿 斌

《數學課程標準（2011年版）》關于教材編寫建議中指出：數學教材為學生的數學學習活動提供了學習主題、基本線索和知識結構，是實現數學課程目標、實施數學教學的重要資源。對于教師而言，要合理地把握數學教材，剖析數學知識的“來龍去脈”，力求追本溯源，以實現數學課堂的優化。

一、尋求教材的根源，訴說其“純真”

教師在處理教材時，既要尊重教材，也要創造性地使用教材。只有將教材知識的根源熟記于心，在教學中才會講得“真切”，說得“真實”，教學才會“有本可依”。只有把握這些，教師才能訴之精華，講之到位。數學教師要有對自己所教的學科有追本溯源的態度，在變中找不變的繼承與支撐點，學會回到原點看問題。教材是“教學之本”，尋求教材的根源，尋找專家教材設計的意圖，是教師備好課的基礎，旨在體現課堂教學的“純真”。

如：在四年級上冊《三角形》單元后的練習題中，有這樣一道題：

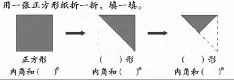
學生完成填空之后，教師并沒有著急學習下一題，而是這樣處理的：

師：做完這道題后你明白了什么？

生：我知道正方形內角和是360°。

生：發現三角形的大小在變化，但三角形的內角和不受影響，都是180°。

師：說得非常好。題目為什么要將正方形和三角形放在一起呢？似乎還要告訴我們什么呢？（學生陷入思考中）

生：我知道了，正方形變成三角形，它的內角和就變了。

生：哦，是的呀！

師：圖形的種類變了，內角和就變了。內角和與圖形的大小沒有關系。

生：不對，正方形的內角和是360°，而長方形的內角和也是360°。

師：這是什么原因呢？難道我們剛才說的結論錯了？

生：正方形是特殊的長方形，圖形的種類沒變。

生：正方形和長方形都是四邊形，四邊形的內角和是360°。

師：是嗎？你們能再舉個例子嗎？

生：平行四邊形。

（教師在黑板上畫出一個平行四邊形）

師：它的內角和是360°嗎？

生：不知道，得量一下。

……

從此環節設計中看出，教師將教材練習進行了“進一步加工處理”，并不是直接就題講題，一帶而過，而是充分理解教材，抓住教材根源，讓學生深入思考，有效地利用教材，利用好本題。不難看出，教師在理解和處理教材時，把握其根源，發揮教材的價值，呈現出題目的價值，將本題教學價值最大化。教學過程中，教師沒有附加的“修飾”和“渲染”，而是利用教材一題，師生的問答，步步深入思考和探索，促進學生思維的發展，訴其教學的“純真”。由此可見，課堂教學期望的是學生“自由、自主、自信”地開展學習活動，就需要教師在備課中準確把握知識的本質屬性，合理設置學習目標。在此基礎之上，“把目標變成學習任務，把教材根源變成學生知識的生長點”，讓學生在課堂的學習活動中“善做、真學”。

二、追求知識的起源，訴說其“歸真”

數學知識的教學應追求其起源，因為數學知識有著前后聯系、一個整體之說，內在的知識體系前后關聯，每一個新知的學習，都離不開舊知的鋪墊。因而教師在教學設計中要有挖掘知識起源的精神。

例如：六年級《圓的認識》中的一個教學片斷：

師：其實，早在兩千多年前，我國古代就有了關于圓的精確記載，墨子在他的著作中這樣描述道：“圓，一中同長也。”你能理解其中的意思嗎？

生：一中是指一個圓心，同長則指半徑或直徑同樣長。

師：而中國古代的這一發現，要比西方整整早一千多年。聽到這里，同學們感覺如何？

生：特別自豪和驕傲。

生：我覺得我國古代的人民非常有智慧。

師：其實，我國古代關于圓的研究和記載還遠不止這些。《周髀算經》中有這樣一個記載“圓出于方，方出于矩”，是說最初的圓是由正方形不斷地切割而來。現在如果告訴你正方形的邊長是6厘米，你能獲得關于圓的哪些信息？

師：說起中國古代的圓，下面的這幅圖案十分特別（圖略），認識嗎？

生：陰陽太極圖。

師：細細看來，陰陽太極原來是由一個大圓和兩個同樣大的小圓組合而成。現在如果告訴你小圓的半徑是3厘米，你又能知道些什么呢？

……

在這“圓的歷史文化”一環節中，充分看出教師追求知識的起源及內在的關系，將知識結構進一步提煉和完善，表達了對數學文化的一種解讀，努力將圓所具有的文化特性浸潤于學生的心間，成了學生數學成長的不竭動力源泉。

數學知識體系基本上是由概念、判斷和推理構成的。概念教學首要是保證概念理解上的確定性和真實性，要追求知識的起源，揭示其內涵和外延，了解其概念之間的關系。課堂教學中切不可模棱兩可、似是而非，更不可自相矛盾。由此，抓住了知識的“生長點”，體現數學知識起源中的文化特性，此教學過程的真實發生必將利于數學課堂教學“歸于其真”。

三、探求教學的本源，訴說其“本真”

作為教師應有探求教學本源的觀念，以發展的思維構建“本真”的數學課堂。數學的教學，不是教師把知識簡單地傳遞給學生，而是由學生基于自己經驗的主動建構過程。這種知識的構建需要教師達成學生學習活動的目標，以“學生發展本位”、“課堂學習本真”為基礎，著眼于學生“最近發展區”，發揮其潛能，向著最高水平發展。

如：五年級上冊《平行四邊形的面積》教學中，第二環節動手操作，探究發現：

1.猜測平行四邊形的面積求法。

師：你認為平行四邊形的面積是怎樣計算的？

生：平行四邊形的面積=底邊×鄰邊=9×5=45（平方厘米）

師：究竟這個猜想是否正確，下面我們一起驗證一下。（課件演示）通過數方格的方法得知，平行四邊形的面積是36平方厘米，不是猜想的45平方厘米，相鄰兩條邊的乘積不能算出平行四邊形的面積。

師：用相鄰的兩條邊相乘不能算出平行四邊形的面積，那該怎樣計算呢？

2.動手操作。

師：我們能不能像剛才一樣，運用轉化思想，把平行四邊形轉化成我們學過的圖形呢？（能轉化）可以轉化成什么圖形？（轉化成長方形）現在我們就小組合作，動手操作，把平行四邊形轉化成已學過的圖形。

3.匯報展示。

學生匯報剪拼的過程和轉化圖形與原來平行四邊形面積的關系。教師引導總結出平行四邊形面積的計算公式。

教師在本環節中，并不是急于告訴學生如何進行平行四邊形的面積計算，而是通過猜測和驗證兩個過程教授于學生，可見教師充分把握住了教材設計的本質，一步步引導學生主動探究和發現。在合作探索和交流中，體現學生的主體地位，發展其觀察、抽象思維能力，以實現數學思想構建的模型化和“本真”化。