簡并態鍺在大注入下的自發輻射譜模擬?

汪建元 林光楊 王佳琪 李成

(廈門大學物理學系,協同創新中心,半導體光子學研究中心,廈門 361005)

1 引 言

鍺(Ge)由于具有準直接帶特性及與硅(Si)工藝相兼容等優勢被認為是硅基光源的理想候選材料之一.理論計算[1]及實驗結果[2]已證實室溫下鍺的直接帶隙與間接帶隙差僅為136 meV,并且在張應變下該帶隙差能進一步減小,有助于提高鍺的發光效率.在鍺中引入約2%的張應變時,鍺能轉變為直接帶隙半導體.另一方面,相比于本征鍺,n型摻雜鍺在相同注入水平下有更多的電子可以被注入到Γ能谷中,因而提高鍺中n型摻雜濃度是提高鍺發光效率的另一種途徑[3].基于應變能帶工程以及n型重摻雜手段,已有關于鍺的直接帶光致發光以及電致發光的大量報道[4?10].然而受工藝限制,在器件制備中能在鍺里引入的張應變仍有限,鍺的直接帶發光一般是在簡并態(大注入或n型重摻雜)下實現的.Schubert等[11]提出的自發輻射理論是基于玻爾茲曼近似推導的,適用于注入水平足夠低的情形.對于簡并態材料的發光,該理論已不適用.目前,對簡并態材料自發輻射性質的研究仍很少,例如發光峰位以及發光強度在不同注入水平的變化等.要精確地分析自發輻射譜,對簡并態材料的自發輻射性質的系統研究必不可少.

本文借助matlab編程計算了鍺在1019—1020cm?3注入載流子水平下的直接帶自發輻射性質.首先討論了在不同應變水平及溫度下鍺準費米能級的變化;然后基于費米狄拉克載流子分布模型系統地研究了應變水平、樣品溫度、摻雜類型及摻雜濃度對發光峰位和m因子的影響.本文的計算結果可以為其他簡并材料發光性質的研究提供參考.

2 應變及溫度對準費米能級的影響

準費米能級反映了材料中非平衡載流子的填充水平,決定了材料的自發輻射強度.在計算材料自發輻射譜之前,有必要探討應變及溫度對材料準費米能級的影響.簡并態下,鍺中載流子與準費米能級的關系可以用(1)式來表示[12]:

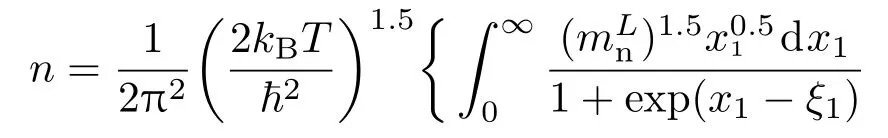
(1)式中,n和p為電子和空穴濃度;kB為玻爾茲曼常數;T為樣品溫度;mLn和mΓn為L和Γ能谷中的態密度有效質量;mlh和mhh為輕空穴帶和重空穴帶的態密度有效質量;EFn和EFp為電子和空穴的準費米能級.L和Γ能谷能量差(ΔEΓ,L)以及輕重空穴帶能量差(ΔElh,hh)取決于應變水平.室溫下,對體鍺而言,ΔEΓ,L=136 meV,ΔElh,hh=0 meV.在沿[001]的雙軸張應變(ε//)下,鍺各帶邊的移動可以表示為[13]

式中,αΓ,αL和αV分別為Γ能谷、L能谷和價帶的靜水壓形變常數;c12和c11為彈性常數;Δ0為自旋-軌道劈裂能;b001為剪切形變常數,δE001=為剪切形變勢能.值得注意的是,ΔEΓ,L也與溫度有關.根據Varshini定律[14],當溫度大于300 K時,鍺直接帶隙和間接帶隙的減小量為

式中p1≈?4.2×10?4eV/K,p2≈?3.6×10?4eV/K;ΔT為樣品溫度相對室溫的變化.因此,同時考慮應變和樣品溫度的作用后,ΔElh,hh和ΔEΓ,L可以表示為

計算過程中所用的鍺相關參數列于表1中(m0為電子靜止質量)[13,15?17].

表1 計算鍺準費米能級所用的參數Table 1.Parameters used for calculation of quasi-Fermi level of Ge.

2.1 應變對準費米能級的影響

圖1示出了室溫下鍺在?1%—2%應變范圍內的載流子濃度與準費米能級的關系.可以看出,當鍺中應變小于2%時,應變對電子準費米能級的影響幾乎可以忽略;當鍺中應變達到2%后,在相同載流子濃度下,鍺的電子準費米能級顯著升高.電子準費米能級的這種變化與電子在L和Γ能谷的競爭分布有關.由于L能谷的態密度遠大于Γ能谷的態密度,當鍺中應變小于2%時,鍺為間接帶隙半導體,電子優先填充L能谷,因而應變對電子準費米能級影響很小;當鍺中應變達到2%時,鍺轉變為直接帶隙半導體,電子優先填充Γ能谷,因而電子的準費米能級顯著升高.空穴也有類似的現象:在壓應變下,空穴優先填充態密度有效質量大的重空穴帶,應變對空穴的準費米能級影響很小;在張應變下,空穴優先填充在態密度有效質量小的輕空穴帶,且隨著應變增大,輕、重空穴價帶頂能量差增大,因而空穴的準費米能級隨張應變的提高顯著降低.

圖1 (網刊彩色)室溫下鍺在?1%—2%應變范圍內的(a)電子濃度與電子準費米能級的變化關系及(b)空穴濃度與空穴準費米能級的變化關系Fig.1.(color online)For Ge under various strains at room temperature,(a)relationship between electron concentration and quasi-Fermi level position of electron,and(b)relationship between hole concentration and quasi-Fermi level position of hole.

2.2 溫度對準費米能級的影響

圖2 示出了受1%張應變的鍺在300—425 K范圍內載流子濃度與準費米能級的關系.隨著溫度的升高,載流子在能帶中的分布更加彌散,需要更多的載流子濃度來維持準費米能級的位置.由于導(價)帶的態密度與導(價)帶到導(價)帶底(頂)能量差的平方根成正比,在能帶更高能處,溫度對準費米能級的影響減弱.

3 簡并態鍺的自發輻射

對于鍺直接帶發光,光子能量E與倒格矢k的關系可表示為

圖2 (網刊彩色)受1%張應變的鍺在300—425 K溫度范圍內的(a)電子濃度與電子準費米能級的關系圖及(b)空穴濃度與空穴準費米能級的關系圖Fig.2.(color online)For Ge under various temperatures with 1%strain,(a)relationship between electron concentration and quasi-Fermi level position of electron,and(b)relationship between hole concentration and quasi-Fermi level position of hole.

其中m?eΓ=0.038m0為Γ能谷中電子有效質量,m?h=0.043m0或m?h=0.284m0為輕空穴或重空穴有效質量.Eg,Γ為鍺的直接帶帶隙,由第2部分可推知其與溫度和應變的依賴關系為

式中,Eg,Γ0=0.802 eV為室溫下(300 K)體鍺的直接帶隙.

在重摻雜或大注入下,鍺處于簡并態,此時直接帶發光強度(I)隨光子能量(hν=E(k))的分布可表示為

式中,mr=mΓnmh/(mΓn+mh)為態密度折合有效質量,mh=mlh或mhh;fe,Γ(k)和fh(k)為電子在Γ能谷及價帶中空穴的費米狄拉克分布函數;EC,Γ和EV,Γ分別為Γ能谷谷底和價帶頂的能量.為了便于分析,所有自發輻射譜都經過相同的歸一化處理.

3.1 溫度和應變對自發輻射譜的影響

圖3(a)為1%張應變本征鍺在5×1019cm?3載流子注入濃度下的Γ-hh躍遷自發發射譜.模擬的樣品溫度為300—425 K.隨著溫度的升高,鍺的帶隙減小、載流子在能帶中的分布更加彌散,因而自發輻射譜的峰值位置向低能端移動并且譜的半高寬增大.雖然在更高溫度下,載流子在價帶和導帶中的占據概率降低,但是由于Γ能谷和L能谷的能量差減小,使得有更多的電子填充到Γ能谷中,因而自發發射譜的峰值強度隨溫度的升高反而增大.另外,當樣品溫度升高時,激發到Γ能谷及價帶中的載流子總數目變多,因而鍺的自發輻射積分強度也隨著溫度的升高而增大.

圖4(a)為不同應變下本征鍺在5×1019cm?3注入載流子濃度下的Γ-hh躍遷室溫自發發射譜.隨著應變的增大,自發輻射譜的半高寬、峰值強度和積分強度也都隨之增大.自發輻射強度的增大是由于應變的引入減小了L能谷和Γ能谷的能量差,使得有更多的電子能散射到Γ能谷中參與自發輻射.當鍺中引入0.8%張應變時,自發輻射的峰值強度和積分強度相比無應變鍺的情形都提高了10倍左右,與文獻[18]報道的光致發光測試結果一致.從圖中還可以看出,雖然Γ-hh躍遷自發輻射的峰值強度大于Γ-lh躍遷自發輻射的峰值強度,但它們的積分強度幾乎相等.這是由于雖然輕空穴帶態密度更小,但空穴在其中的能量分布更加彌散.

圖3 (網刊彩色)(a)本征鍺在5×1019cm?3注入載流子濃度、1%張應變下Γ能谷電子重空穴躍遷自發發射譜隨溫度的變化及對應的(b)峰值強度、(c)積分強度隨溫度的變化Fig.3. (color online)(a)Calculation of spontaneous emission spectra from Γ-hh recombination in intrinsic Ge with injection carrier concentration of 5×1019cm?3under 1%strain at various sample temperature and corresponding dependence of(b)peak intensity and(c)integrated intensity on sample temperature.

圖4 (網刊彩色)(a)室溫時本征鍺在5×1019cm?3注入載流子濃度、不同應變下的Γ-hh躍遷自發發射譜及其與Γ-lh躍遷自發發射譜的(b)峰值強度、(c)積分強度隨應變的變化Fig.4.(color online)(a)Calculation of spontaneous emission spectra from Γ-hh transition of intrinsic Ge under various strains at room temperature with injection carrier concentration of 5×1019cm?3;variation of(b)peak intensity and(c)integrated intensity of spontaneous emission spectra from Γ -hh and Γ -lh transitions versus the strain level in Ge.

3.2 摻雜類型及摻雜濃度對自發輻射譜的影響

圖5 (a)和圖5(b)分別示出了p型摻雜濃度對0.2%張應變鍺和1%張應變鍺在1×1019cm?3注入載流子濃度下的室溫Γ-lh躍遷自發發射譜的影響.計算的p型摻雜濃度范圍為1×1018cm?3至5×1019cm?3.為了更直觀地研究自發輻射強度的變化,忽略了重摻雜下的能帶縮減效應[19].可以看出,對于0.2%張應變鍺,其自發輻射強度隨著p型摻雜濃度的增大略微增大.然而,當鍺中張應變增大到1%時,p型摻雜濃度的增加對自發輻射強度的增大變得更小.圖5(c)定量地顯示了不同p型摻雜濃度下自發輻射譜峰值強度相比于本征鍺的提高倍數.隨著受主濃度的增加,自發輻射譜峰值強度的增強迅速達到飽和值.在5×1019cm?3受主濃度下,0.2%張應變鍺的峰值強度相比本征鍺僅提高了約20%,對1%張應變鍺僅提高了約7%.上述結果表明,p型摻雜并不能有效地提高鍺的自發輻射強度.

為了對比,同時模擬了n型摻雜濃度對鍺自發發射譜的影響.圖6(a)和圖6(b)示出了n型鍺在與圖5(a)和圖5(b)相同應變水平和注入載流子濃度下的自發發射譜.圖6(c)為不同n型摻雜濃度下鍺相比于本征鍺的自發發射譜峰值強度增強因子隨n型摻雜濃度的變化.可以看出,隨n型摻雜濃度的增加,自發發射譜的峰值強度顯著增大.對于0.2%張應變鍺,在1×1019cm?3和5×1019cm?3n型摻雜濃度下,自發發射譜峰值強度分別增強了約1.7倍和約22.6倍.當鍺中張應變增大到1%,自發發射譜峰值強度增強因子仍大于約1.5倍和9.8倍.上述結果說明n型摻雜能大大提高鍺的自發輻射強度.

3.3 摻雜、應變及溫度對自發輻射峰值強度m因子的影響

通過L-Im關系擬合LI曲線可以提取出自發輻射譜的m因子,以定量表征材料的自發輻射性質.大多數情況下,載流子的注入濃度(Δn)近似正比于注入電流(I)[20].因而,m因子可以通過線性擬合logL-logΔn曲線得到.

圖5 (網刊彩色)(a)0.2%張應變Ge及(b)1%張應變Ge在1×1019cm?3注入載流子濃度、不同p型摻雜濃度下的室溫Γ-lh躍遷自發發射譜;(c)上述模擬條件下的峰值發光強度與本征鍺的比值隨p型摻雜濃度的變化;上述計算過程中忽略了重摻雜引起的能帶縮減效應Fig.5.(color online)The spontaneous emission spectra for Ge under various p-type doping concentrations(a)with 0.2%tensile strain and(b)with 1%tensile strain under injection carrier concentration of 1×1019cm?3at room temperature from Γ-lh transition;(c)the amplif i cation of peak intensity compared to that of intrinsic Ge under p-type doping.The effect of band gap narrowing by heavy doping is neglected.

圖6 (網刊彩色)(a)0.2%張應變Ge及(b)1%張應變Ge在1×1019cm?3注入載流子濃度、不同n型摻雜濃度下的室溫Γ-lh躍遷自發發射譜;(c)上述模擬條件下的峰值發光強度與本征鍺的比值隨n型摻雜濃度的變化;上述計算過程中忽略了重摻雜引起的能帶縮減效應Fig.6.(color online)The spontaneous emission spectra for Ge under various n-type doping(a)with 0.2%tensile strain and(b)with 1%tensile strain under injection carrier concentration of 1×1019cm?3at room temperature from Γ-lh transition;(c)the amplif i cation of peak intensity compared to that of intrinsic Ge under n-type doping.The effect of band gap narrowing by heavy doping is neglected.

圖7(a)示出了n型摻雜濃度對體鍺室溫自發輻射譜m因子的影響.由于施主雜質能額外提供電子,隨著n型摻雜濃度的增大,m因子逐漸變小.在注入載流子濃度分別為1019,1020cm?3下,當鍺中施主雜質為5×1019cm?3時,m因子分別從本征鍺的1.64,2.60減小至0.75,1.30.當鍺中存在張應變時,Γ能谷和L能谷的能量差減小,在相同注入水平下有更多的電子能填充至Γ能谷中.因此,m因子隨鍺中張應變水平增大而減小(圖7(b)).在1019cm?3注入載流子濃度下,當鍺中張應變為2.0%時,m因子從體鍺的1.64減小至0.90.

圖7 (網刊彩色)(a)室溫下體Ge自發輻射譜m因子隨n摻雜濃度的變化;(b)室溫下本征Ge自發輻射譜m因子隨張應變的變化Fig.7.(color online)(a)The dependence of m factor for spontaneous emission spectra of bulk Ge on n-type doping concentration at room temperature;(b)the dependence of m factor for spontaneous emission spectra of intrinsic Ge on tensile strain at room temperature.

圖8 (a)和圖8(b)分別為無應變本征鍺及1%張應變本征鍺的自發輻射m因子隨溫度的變化.對于無應變本征鍺,在1019cm?3注入載流子濃度下,m因子從300 K下的1.64略微減小至425 K下的1.6;在1020cm?3注入載流子濃度下,m因子從300 K下的2.60減小至425 K下的1.94.對于1%張應變本征鍺,m因子幾乎和溫度無關,且隨著注入載流子濃度的增加,m因子從1019cm?3的1.50減小至1020cm?3的1.01.這些結果表明張應變能提高鍺自發輻射的溫度穩定性.

圖8 (網刊彩色)(a)無應變本征鍺及(b)1%張應變本征鍺自發輻射譜m因子隨溫度的變化Fig.8.(color online)The dependence of m factor for spontaneous emission spectra of intrinsic Ge(a)without strain and(b)with 1%tensile strain on sample temperature.

4 結 論

本文模擬并分析了應變、溫度以及摻雜對簡并態鍺自發輻射譜的影響.在1019—1020cm?3注入載流子濃度范圍內,壓應變對準費米能級的影響可以忽略,而張應變有助于提高載流子的填充水平,從而大大增強了自發輻射強度.隨著溫度的升高,Γ能谷和L能谷間的能量差減小,同時有更多的電子(空穴)被激發到導帶(價帶)中.因而,雖然在更高溫度下載流子在能帶中的分布更加彌散,自發發射譜的峰值強度和積分強度仍隨溫度升高而增大.計算結果表明,在鍺中引入受主雜質對自發發射譜強度的影響很小,而在鍺中引入施主雜質能極大地提高自發發射譜強度.對L-Δn曲線m因子的研究表明,張應變可以提高鍺自發輻射的溫度穩定性.本文的模擬結果對于其他的簡并態材料自發輻射性質的研究起著指導意義.

[1]Sun X C,Liu J F,Kimerling L C,Michel J 2010IEEE J.Sel.Top.Quantum Electron.16 124

[2]Ghrib A,Kersauson M D,Kurdi M E,Jakomin R,Beaudoin G,Sauvage S,Fishman G,Ndong G,Chaigneau M,Ossikovski R,Sagnes I,Boucaud P 2012Appl.Phys.Lett.100 201104

[3]Cai Y,Han Z H,Wang X X,Rodolfo E,Aguilera C,Kimerling L C,Michel J,Liu J F 2013IEEE J.Sel.Top.Quantum Electron.19 1901009

[4]Lin G Y,Wang C,Li C,Chen C W,Huang Z W,Huang W,Chen S Y,Lai H K,Jin C Y,Sun J M 2016Appl.Phys.Lett.108 191107

[5]Michael O,Martin G,Daniel W,Marc S,Mathias K,Erich K,J?rg S 2013Opt.Express21 2206

[6]Lin G Y,Yi X H,Li C,Chen N L,Zhang L,Chen S Y,Huang W,Wang J Y,Xiong X H,Sun J M 2016Appl.Phys.Lett.109 141104

[7]Bernhard S,André K,Martin K,Michael O,Erich K,J?rg S 2014Phys.Status Solidi C11 1686

[8]Liu Z,Hu W X,Li C,Li Y M,Xue C L,Li C B,Zuo Y H,Cheng B W,Wang Q M 2012Appl.Phys.Lett.101 231108

[9]Lin G Y,Chen N L,Zhang L,Huang Z W,Huang W,Wang J Y,Xu J F,Chen S Y,Li C 2016Materials9 803

[10]Rodolfo E,Camacho A,Cai Y,Neil P,Bessette J T,Marco R,Kimerling L C,Jurgen M 2012Opt.Express20 11316

[11]Schubert E F,Gessmann T,Kim J K 2005Light Emitting DiodesKirk-Othmer Encyclopedia of Chemical Technology

[12]Huang S H,Li C,Chen C Z,Zheng Y Y,Lai H K,Chen S Y 2012Acta Phys.Sin.61 036202(in Chinese)[黃詩浩,李成,陳城釗,鄭元宇,賴虹凱,陳松巖 2012物理學報61 036202]

[13]van de Walle C G 1989Phys.Rev.B39 1871

[14]Varshni Y P 1967Physica34 149

[15]Liu J F,Cannon D D,Kazumi W,Yasuhiko I,David T D,Samerkhae J,Michel J,Lionel C K 2004Phys.Rev.B70 155309

[16]Wortman J J,Evans R A 1965J.Appl.Phys.36 153

[17]Cheng S L,Lu J,Shambat G,Yu H Y,Saraswat K,Vuckovic J,Nishi Y 2009Opt.Express17 10019

[18]Capellini G,Reich C,Guha S,Yamamoto Y,Lisker M,Virgilio M,Ghrib A,Kurdi M E,Boucaud P,Tillack B,Schroeder T 2014Opt.Express22 399

[19]Rodolfo C A,Han Z H,Cai Y,Lionel C K,Jurgen M 2013Appl.Phys.Lett.102 152106

[20]Hu W X,Cheng B W,Xue C L,Xue H Y,Su S J,Bai A Q,Luo L P,Yu Y D,Wang Q M 2009Appl.Phys.Lett.95 092102