煤礦瓦斯涌出時序預測的自組織數據挖掘方法*

李潤求，吳瑩瑩，施式亮，朱紅萍

(1.湖南科技大學 資源環境與安全工程學院， 湖南 湘潭 411201; 2.煤礦安全開采技術湖南省重點實驗室， 湖南 湘潭 411201;3.湖南科技大學 信息與電氣工程學院， 湖南 湘潭 411201)

數字出版日期： 2017-07-19

0 引言

復雜系統是由存在復雜相互作用的諸多變量組成，人們不能獲得系統的全部變量，也難以建立確定性的多因素數學模型來描述系統演化，但系統演化中存在的大量時間序列模式是復雜系統非常重要的基本特征，不同的時間序列模式代表了系統演化的周期、趨勢以及系統變量之間的關系[1-2]。瓦斯災害是煤礦安全生產的典型災害。瓦斯涌出與煤巖瓦斯含量、開采規模、生產工藝、通風方式等多種因素有關，瓦斯災害子系統既受瓦斯賦存地質條件的影響，同時也受煤礦安全生產系統其他因素和其他子系統的影響，具有復雜非線性系統的典型特征，目前仍不能確切知道影響瓦斯涌出子系統狀態的變量數，但可以通過時間序列來刻畫安全生產系統的動力學演化特性[3]。因而，時間序列預測建模在煤礦瓦斯涌出預測中仍然是最基本最常用的方法，如線性回歸、灰色理論預測[4]、人工神經網絡預測[5]等，特別是人工神經網絡預測建模方法，由于其對復雜系統的適應性強且預測精度高得到了大量應用。

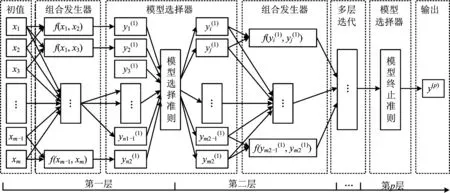
圖1 自組織數據挖掘算法結構Fig.1 Structure of self-organizing data mining algorithm

自組織數據挖掘(self-organizing data mining, SODM)是在烏克蘭科學院院士Ivakhnenko提出的數據分組處理方法(group method of data handling, GMDH)基礎上逐漸發展起來的數據分析方法，是一種遺傳、變異、進化與篩選的演化方法[6]，通常也歸屬于神經網絡方法。該方法以簡單多項式作為傳遞函數，產生大量不斷增長復雜度的候選模型，根據給定的內準則和外準則對候選模型進行篩選，直至篩選的模型在觀測樣本產生過擬合為止，最終獲得高階Kolmogorov-Gaber(簡稱K-G)多項式最優模型[7-8]。SODM是復雜多變量系統的一種啟發式自組織方法，其能在系統結構未知的情況下，根據少量的輸入輸出數據，建立其數學模型，在解決復雜非線性系統研究方面具有運用系統先驗知識、歸納學習的算法等在復雜系統的多因素模擬演化、預測建模等方面得到廣泛應用，但其應用領域目前主要集中在經濟、金融、商業等方面[9-10]，在煤礦瓦斯涌出時序預測建模以及安全生產與災害防控研究中鮮有發現。因此，筆者嘗試將SODM方法引入到煤礦瓦斯涌出復雜系統的時間序列預測建模中，首先對瓦斯涌出時間序列進行相空間重構(reconstructed phase space, PSR)[11-13]獲得系統演化基本參數，然后應用非線性傳遞函數迭代逐步建立系統演化的K-G多項式最優復雜度函數，并應用實例驗證其在安全生產時序預測中適應性和可靠性，以期通過SODM方法探索復雜安全生產系統的演化軌跡，為安全預測提供新方法。

1 PSR-SODM預測建模方法

1.1 SODM基本原理

SODM思想是1967年烏克蘭科學院Ivakhnenko院士提出的，其理論基礎是物種選擇學說。生物圈是復雜非線性系統，生物在不斷受外界制約與環境協調的演化過程中，物競天擇，適者生存，自組織協調發展，形成物種遺傳與進化。SODM正是借鑒生物選擇的復雜系統自組織特性，采用通用迭代算法，由初始簡單模型開始逐步構建最優復雜模型，整個建模過程是完全自我組織的過程。SODM的基本原理如下[7-8]：

對于復雜系統，設有m維輸入變量X=[x1,x2,…,xm]，一個輸出變量為y，如果輸入與輸出存在：

y=g(X)=g(x1,x2,…,xm)

(1)

則函數g(·)可以展開成離散形式的Volterra多項式級數(K-G多項式)：

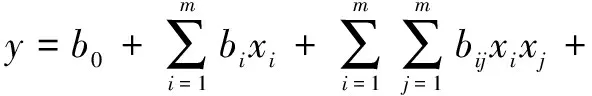
(2)

式中:b0,bi,bij,bijk為待定系數。

對一任意非線性函數，在理論上均可以通過式(2)進行逼近。但隨著輸入變量的增加，式(2)的項數會急劇增加，亦即建模所估計的待定系數會急劇增加，與此同時，所需要的樣本數量也會急劇增加，并且還會造成計算工作量的急劇增加和計算上的不穩定性。

為解決上述問題，Ivakhnenko提出了通過“分層部分實現”來達到“完全實現”，如圖1，即可以利用任意2個輸入變量構造傳遞函數，通過多層迭代運算來達到式(2)的完全實現，即GMDH算法[7-8]。

Ivakhnenko給出了若干基本傳遞函數f(·)，其中應用較多的f(·)有：

f(xi,xj)=b0+b1xi+b2xj

(3)

(4)

式中:i,j=1,2,…,m，i≠j，b0,b1,b2,b3,b4,b5為待定系數。

(5)

由此可得到由多層f(·)復合構成的復雜g(·)即為尋求的預測函數。

SODM方法在進行建模時，并不需要預先設置參數和最終模型形式，而是通過構建簡單傳遞函數的自組織方式來逐步確定輸入變量與輸出變量之間的復雜關系，整個建模過程是完全自我組織的過程。因而，SODM方法對于復雜系統數據分析有獨特優勢。

1.2 PSR

Takens[11]，Packard[12]等認為可以用原始系統中某個變量的延遲坐標來PSR，重構的相空間的軌跡反映了系統狀態的演化特性。PSR雖然是用單個變量在不同時刻的值構成相空間，但動力學系統的單個變量的變化跟此變量與系統的其他變量的相互作用有關，即該變量的時間序列隱含著系統的動力學特性。

對于長度為N的一維時間序列x(t)(t=1,2,…,N)，選擇合適嵌入維數m和延遲時間τ，重構的相空間與原系統具有相同的拓撲性質：

X(i)=[x(i-(m-1)τ),x(i-(m-2)τ,...,x(i)]

(6)

式中：X(i)表示i時刻系統的動力學狀態；i=(m-1)τ+1,(m-1)τ+2,…,N。

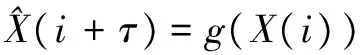
(7)

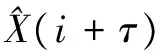
y(i+τ)=g(x(i-(m-1)τ),x(i-(m-2)τ),…,x(i))

(8)

1.3 C-C方法

嵌入維數m和延遲時間τ直接影響重構相空間的質量，C-C方法通過序列的關聯積分進行τ和m聯合確定。通過關聯積分和延遲時間的關系計算出τ和嵌入窗寬τw，從而確定m。C-C方法在相空間重構中應用較廣，其計算過程如下[13-14]。

對于一維時間序列x(i)(i=1,2,..,N) ，可平均分為T個子序列：

(9)

采用分塊平均策略按式(10)計算關聯積分統計量：

(10)

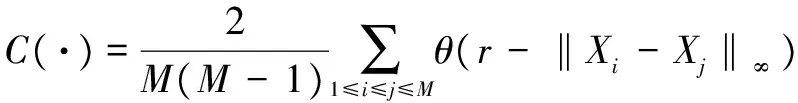
對于獨立同分布的序列x(i)(i=1,2,..,N) ，固定m和t，則當N→∞，均有S(M,r,t)=0。但實際上序列x(i)(i=1,2,..,N)不可能無限且變量會存在某種相關性，因此，可選擇合適r所對應的最大值和最小值，計算其差量：

ΔS1(m,t)=max{S1(m,ri,t)}-min{S1(m,ri,t)}

(11)

則τ可取ΔS1(m,t)～t的第一個局部極小點或第一個0點。

根據Brock-Dechert-Scheinkman統計結論[14]，取M=2,3,4,5，r=j×0.5σ(j=1,2,3,4,σ為序列的標準差)，計算檢驗統計量：

(12)

S1_cor(t)的全局最小點即為τw的最優值，則可按式(13)計算序列最佳嵌入維數m：

(13)

1.4 預測建模

根據PSR理論和SODM方法，可以將兩者有機結合起來進行煤礦瓦斯涌出一維時間序列進行預測建模，建模過程如下：

1)獲取煤礦瓦斯涌出一維時間序列，設為x(t)(t=1,2,…,N)，N為序列長度。

2)應用C-C方法獲得x(t)的m和τ，按照式(8)進行PSR，視[x(i-(m-1)τ),x(i-(m-2)τ),…,x(i)]為系統m維自變量，y(i)為一維因變量，形成樣本數據集。

3)對樣本集劃分為訓練子集、測試子集和預測子集3部分，子集的長度可按N的一定比例劃分，一般認為訓練子集長度應超過N的50%才能取得較好的訓練效果。

4)構造傳遞函數f(·)。對于煤礦復雜安全生產系統，瓦斯涌出影響因素之間存在非線性關系，通常選擇式(4)作為傳遞函數就能較好地形成最終的非線性預測模型。

5)按照f(·)要求將m維自變量兩兩組合，通過訓練子集應用內準則估計f(·)的待定系數，內準則通常可以采用最小二乘法準則。

6)傳遞函數選擇。選擇合適的外準則，并通過測試子集保留符合外準則要求的部分最優傳遞函數。外準則常用的有殘差、相對誤差、方差、均方差等。

7)以傳遞最優函數的輸出作為下一層f(·)的輸入。

8)重復步驟5)，6)，7)，不斷產生后續層次的傳遞函數，直到外準則取得最小值時獲得最優復雜度模型g(·)，算法終止。

9)利用獲得的g(·)對預測子集進行預測，并通過預測模型檢驗指標檢驗預測效果。

2 應用實例

根據湘煤集團某礦安全監測數據，3162回采工作面在2014年11月15—24日的瓦斯涌出量為4.00～5.20 m3/min，平均瓦斯涌出量為4.57 m3/min，瓦斯涌出不均衡系數為1.14，如圖2。

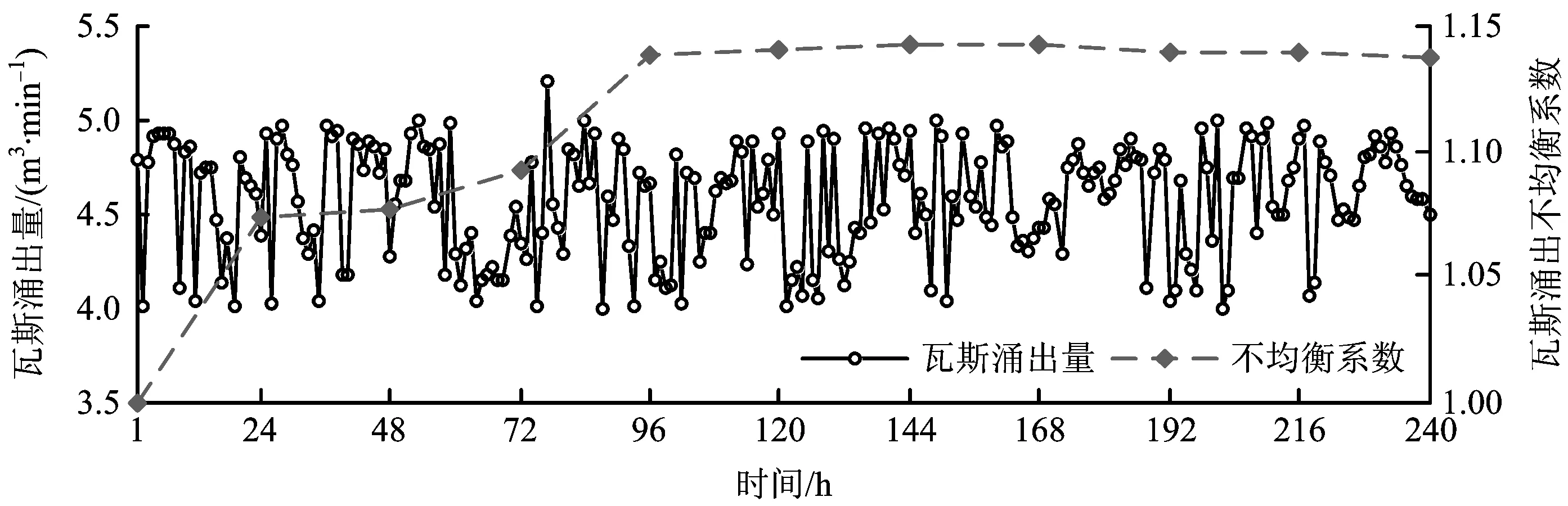
圖2 3162回采工作面瓦斯涌出量Fig.2 Gas emission in 3162# mining workface

根據時序預測的PSR-SODM方法建模步驟，應用C-C方法計算獲得瓦斯涌出時間序列m=4，τ=2。對序列進行PSR后，按原始序列長度的80%，10%，10%劃分訓練子集、測試子集和預測子集，則3個子集的長度分別為184，24，24。由圖2可知，瓦斯涌出量是非線性時間序列，因此選擇式(4)作為傳遞函數進行迭代計算，其中內準則選用最小二乘法，外準則選用最小相對誤差。瓦斯涌出量擬合和預測結果如圖3，相對誤差如圖4，擬合相對誤差為-6.406 7%～6.459 1%，擬合平均相對誤差絕對值為1.4679%，預測相對誤差-5.751 7%～6.049 3%，預測平均相對誤差絕對值2.145 7%，瓦斯涌出量預測效果較好，能滿足煤礦安全生產實際工程應用的需要。

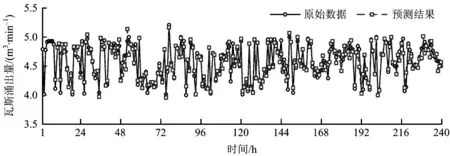
圖3 3162回采工作面絕對瓦斯涌出量預測結果Fig.3 Prediction of gas emission in 3162# mining workface

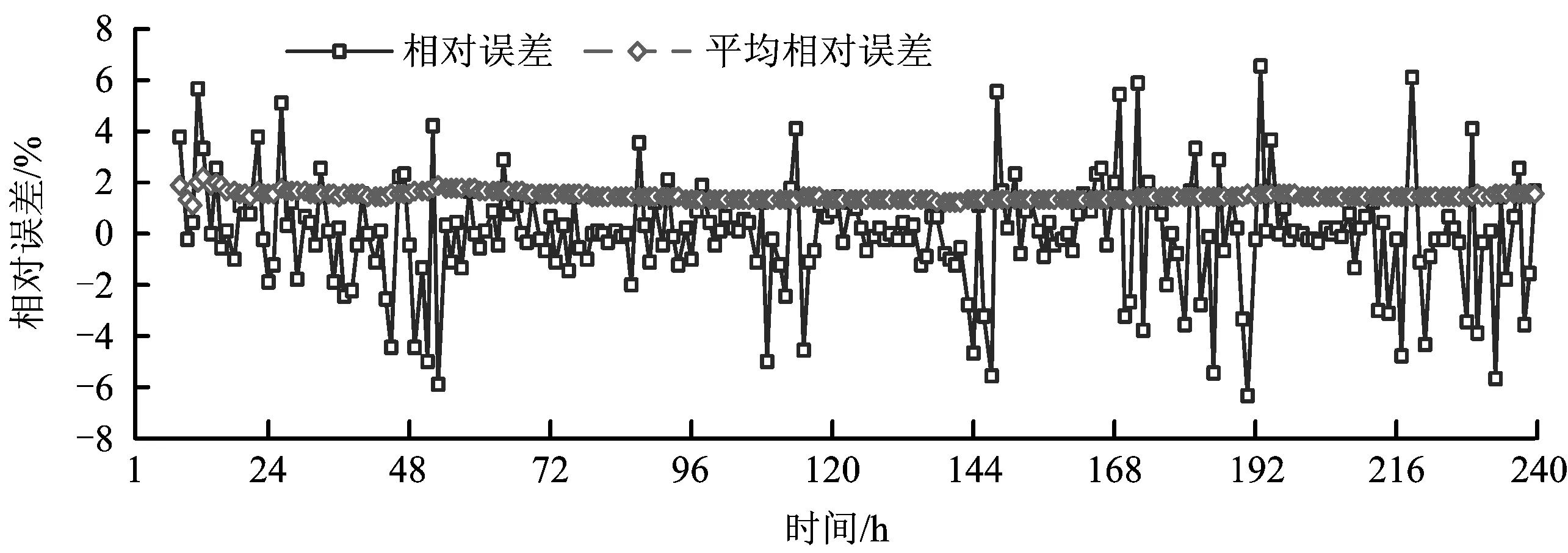
圖4 3162回采工作面絕對瓦斯涌出量預測相對誤差Fig.4 Relative error of gas emission in 3162# mining workface

3 結論

1)安全生產系統是人機環境結構復雜且時空耦合的非線性系統，由于變量繁多且無法完全確定其具體數目，同時變量之間存在多重復雜作用，難以建立統一的、確定性的多因素數學模型來描述安全生產系統演化規律，但系統演化進程中存在的時間序列模式是系統演化特性的客觀反映，可以通過對時間序列進行PSR獲得系統的演化規律。因而，基于時間序列的安全生產規律與預測研究仍然具有重要的理論意義和實用價值。

2)SODM方法以系統變量為輸入，通過傳遞函數的多層迭代來獲得最優復雜度模型，建模過程是自組織過程，能適用于復雜的安全生產系統演化規律分析與安全預測研究。對于安全生產系統中存在的時間序列，可有機結合PSR和SODM方法來分析系統演化特性并進行預測建模，且其預測模型具有較強的可靠性和較高的預測精度，能滿足工程實際應用。

3)在應用SODM對安全生產時間序列進行預測建模時，PSR質量對SODM方法獲得的最終模型的復雜度有一定影響，通過具有客觀性的如C-C方法等對時間序列進行PSR參數確定，可以獲得安全系統演化中隱藏的潛在規律性，并可能提高SODM預測建模質量和預測精度。

[1] 李成剛, 田益祥, 何繼銳. AC算法的EMD分解GMDH組合的預測模型及應用[J]. 系統管理學報, 2012, 21(1): 105-110.

LI Chenggang, TIAN Yixiang, HE Jirui. Prediction model of AC algorithm based on EMD decomposition combined with GMDH and its application [J]. Journal of Systems & Management, 2012, 21(1): 105-110.

[2] 李潤求, 施式亮, 伍愛友, 等. 煤礦瓦斯災害事故的分形特性[J]. 中國安全生產科學技術, 2014, 10(9): 25-29.

LI Runqiu, SHI Shiliang, WU Aiyou, et al. Research on fractal characteristics of gas accident in coal mine[J]. Journal of Safety Science and Technology, 2014, 10(9): 25-29.

[3] 何利文, 施式亮, 宋譯, 等. 回采工作面瓦斯涌出的復雜性及其度量[J]. 煤炭學報, 2008, 33(5): 547-550.

HE Liwen, SHI Shiliang, SONG Yi, et al. Complexity and measurement of complex degree of gas gush in heading faces of coal mine [J]. Journal of China Coal Society, 2008, 33(5): 547-550.

[4] 伍愛友, 田云麗, 宋譯, 等. 灰色系統理論在礦井瓦斯涌出量預測中的應用[J]. 煤炭學報, 2005, 30(5): 589-595.

WU Aiyou, TIAN Yunli, SONG Yi, et al. Application of the grey system theory for predicting the amount of mine gas emission in coal mine [J]. Journal of China Coal Society, 2005, 30(5): 589-595.

[5] 付華,史冬冬. 基于IGA-LSSVM的煤礦瓦斯涌出量預測模型研究[J]. 中國安全科學學報, 2013, 23(10): 51-55.

FU Hua ,SHI Dongdong. Study on gas emission prediction model based on IGA-LSSVM [J]. China Safety Science Journal, 2013, 23(10): 51-55.

[6] Vakhnenko A G, Ivakhnenko G A. The review of problems solvable by algorithms of the group method of data handling (GMDH) [J]. Pattern Recognition and Image Analysis, 1995, 5(4): 527-535.

[7] A.G. Ivakhnenko, G. A. Ivakhnenko, N.M. Andrienko. Inductive computer advisor for current forecasting of ukraine micro economy [J].Systems Analysis Modeling Simulation, 1998, 31(2): 143～151.

[8] LI Runqiu, SHI Shiliang, WU Aiyou, et al. Research on prediction of gas emission based on self-organizing data mining in coal mines [A]. 2014 International Symposium on Safety Science and Technology[C]. 2014: 779-785.

[9] 朱幫助, 張秋菊, 鄒昊飛, 等. 基于OSA算法和GMDH網絡集成的電子商務客戶流失預測[J].中國管理科學, 2011,19(5): 64-70.

ZHU Bangzhu, ZHANG Qiuju, ZOU Haofei, et al. E-Business customer churn prediction based on integration of objective system analysis and group method of data handling network [J]. Chinese Journal of Management Science, 2011, 19(5): 64-70.

[10] 廖志高,謝妮.自組織數據挖掘在電力需求預測中應用[J].電力科學與工程, 2004 (4): 41-45.

LIAO Zhigao, XIE Ni. Application of self organization of data digging in prediction of electricity demand [J]. Electric Power Science and Engineering, 2004 (4): 41-45.

[11] Takens F. Detecting Strange Attractors in Turbulence [A]. Dynamical Systems and Turbulence, Lecture Notes in Mathematics[C]. Berlin:Springer-Verlag, 1981, 898: 366-381.

[12] Packard N H, Crutchfield J P, Farmer J D, et al. Geometry from a time series [J]. Physical Review Letters (S0031-9007), 1980, 45(9):712-716.

[13] 黃寧, 馬林茂. 基于改進C-C方法相空間重構和LS-SVM的隧道拱頂沉降預測模型[J]. 數學的實踐與認識, 2014, 44(20): 130-139.

HUANG Ning, MA Linmao. The prediction model of metro vault settlement based on developed C-C method phase space reconstruction and LS-SVM [J]. Mathematics in Practice and Theory, 2014, 44(20): 130-139.

[14] 陸振波, 蔡志明, 姜可宇. 基于改進的C-C方法的相空間重構參數選擇[J]. 系統仿真學報, 2007, 19(11): 2527-2538.

LU Zhenbo, CAI Zhiming, JIANG Keyu. Determination of embedding parameters for phase space reconstruction based on improved C-C Method[J]. Journal of System Simulation, 2007, 19(11): 2527-2538.