試論高中數學競賽解題技巧
山西省芮城縣芮城中學(044600)
劉書寧●
試論高中數學競賽解題技巧
山西省芮城縣芮城中學(044600)
劉書寧●
在高中數學學習中數學競賽發揮著重要的補充效用,對競賽解題思想和技巧的探討是數學學習一個重要內容.本文從高中學生數學競賽解題技巧的重要性出發,從解題思維和命題解析兩個方面探討具體的解題技巧.
高中數學;競賽;解題技巧
一、高中學生數學競賽解題的重要性
在準備參加全國數學聯賽過程中,我感覺到我同大多數同學一樣,對數學競賽存在畏難、畏懼心理.只有更科學地改進和創新既有的數學學習方式和方法,更好地掌握高中數學競賽解題技巧,以便更好地把抽象性概念轉變成個人理解和數學思維,進而促進我們分析和解決實際問題的能力,實現高中數學學習思維的協調、全面發展.
二、高中數學競賽解題技巧解析
1.命題解析之演繹深化
對于競賽數學題目,要想快而準地解答,首要任務就是對命題進行解析,以明確問題,明晰條件,為解題奠定基礎.演繹深化是對競賽數學題目分析的重要方法.其定義就是以一般性、常規性且正確的基本問題作為出發點,基于邏輯思維循序漸進地演繹和深化數學競賽題目.和傳統解題技巧是相反的,是基于邏輯來分析和掌握問題實質,即從定理、圖形、公式、具體問題等,自淺入深逐步演繹深化出新問題.有諸多數學解題技巧,比如:數形結合、聯想類比等,均可自反向應用到該技巧中.
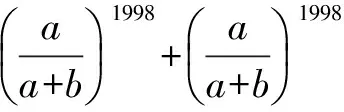
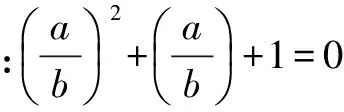
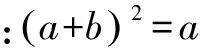
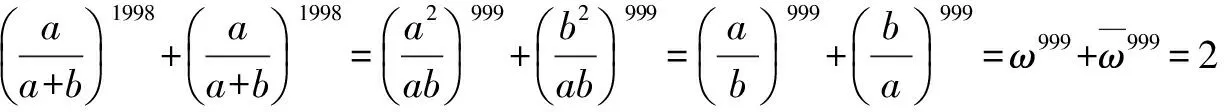
注:本題通過演繹配方,簡化了所求的表達式;巧用1的立方虛根,活用ω的性質,計算表達式中的高次冪.一系列的變換過程,有較大的靈活性,要求我們善于聯想和展開.
2.解題策略之局部思維
(1)分解成多個局部
高中數學競賽中有諸多綜合性題目,因題目相對復雜無法直接解出答案,而需要把具體問題分解成多個部分,再逐一解決進而對整個問題進行有效解決.但是要指出的是,局部問題之間存在一定的獨立性或者遞進性,所以在解決局部問題過程中,必須準確、妥善處理相互間的關系,進而才可確保解題思路的正確.
例2 假設n(>4)是一個給定整數,且x1,x2,x3,…,xn∈[0,1],請證明:
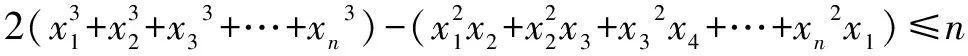

(2)反證法
反證法是高中數學中常用的解題方法,其基本思想就是先提出一個和命題結論完全相反的假設,再通過既有公式、定理等進行一系列正確、嚴密的推理,由此得到新結論,而該結論或和既定條件矛盾,或和既定結論相矛盾,那么該結論就是正確的.此方法是高中競賽解題中常用的方法,能夠迅速明確命題中心內容,找準切入點.應用此方法的步驟有三個:反設;歸謬;結論.其中,反設是最為基本的,歸謬是關鍵.此方法應用推導過程無固定方式,但必須基于反設進行,要不然推導就失去意義.在推導中必須做到嚴謹,所得到的矛盾有這幾種情況:一是和命題已知條件相矛盾;二是和既有定理公式矛盾;三是和反設相矛盾;四是自相矛盾.
例3 在一次國際數學研討大會上有9名數學家做到一起,發現其中任意3個,最少2個可用一種語言交流.假如每名數學家至少會3種語言,那么請證明這9名數學家中,至少有3名能有一種語言進行交流.
解析 可先假定不存在三個人能夠說相同一種語言,那么每種語言最多有2人會說,進而每個人用一種語言最多可和另一人交流.
假設9名數學家分別為M1,M2,M3,…,M9,那么自M1最多能夠說3種語言,所以最少把和另外5個人,可設是M2,M3,M4,M5,M6不能進行交流,同時又因為M2也最多會3種語言,所以其至少和M3、M4,M5,M6中的任何一個人不能交流,可假設是M3,那么M1,M2,M3三個人相互間無法交流,而這和題設是相矛盾的,因此原來的結論是正確的.
總而言之,高中數學競賽解題過程,蘊含著重要的數學思想方法,只有對數學思想、數學方法理解透徹及融會貫通時,才能提出新看法、巧解法.
[1] 陳小瑩,陳宇.一道2014年波羅地海數學奧林匹克不等式的推廣[J]. 中學數學研究,2015(11)
[2] 王慧興.數學奧林匹克訓練題(196)[J]. 中等數學,2015(10)
G632
B
1008-0333(2017)07-0029-01

