探尋解題中的規律方法,體味數學中的和諧統一
江蘇省海門市第一中學(226100)
胡昌亮●
探尋解題中的規律方法,體味數學中的和諧統一
江蘇省海門市第一中學(226100)
胡昌亮●
數學是一個和諧統一的整體,具體知識內容的背后,總是由規律性的思維方法所牽引著.為了帶領學生們找到這個核心線索,作者總結出了一些具有典型意義的規律方法,結合具體問題加以闡述,望對高效教學的開展有所啟發.
高中;數學;規律方法
一、探尋方程思想方法,簡潔高效完成解題
從初中時期開始,學生們就開始接觸方程的知識了.進入高中階段之后,方程的種類與形式繼續擴充,不斷豐富靈活起來.然而,對于方程知識的理解,不能僅僅停留在方程的解答上,而是要站在更高的角度,將之視為一種思維方法,才能最大限度地將方程的價值體現出來.
例如,為了讓學生們體會到方程思想方法的實際運用,我先請學生們思考這樣一個問題:{an}是一個等差數列,且其公差不為零,前n項和是Sn.已知,a3和a7的等比中項是a4,S8的值是32,那么,S10的值是多少?隨后又繼續提問:現有一條拋物線y2=2px(p>0),其焦點是F.過點F做一條傾斜角是45°的直線,使之與拋物線相交于點A和點B.如果線段AB的長是8,那么,p的值是多少?這兩個問題所對應的知識點雖然不同,但其背后所運用到的思想方法卻是相同的.在第一個問題中,學生們需要結合數列的基本知識,根據已知條件列出方程組,對該數列的首項與公差進行求解.而在第二個問題中,學生們則是結合拋物線的內容與弦長公式列出方程,求出p值.由此,學生們發現,方程思想方法在很多領域的問題解答中都是可以適用的,并讓解題過程簡潔了許多.
在很多具體問題的解答當中,方程都會成為一種簡潔高效的分析方法.它的出現,讓很多朦朧問題的思維過程,得以在未知數的輔助下清晰顯現.由此看來,方程儼然已經成為了一種普適性的思想方法,滲透于高中數學的各類問題解答當中.
二、探尋分類思想方法,嚴謹周密完成解題
高中數學的靈活性特征不僅表現在問題形式的多變上,還表現在問題內容的多種可能性上.隨著學習的不斷深入,學生們不難發現,很多問題的解答路徑并不是唯一的,其中常常存在著很多種可能的情況.哪一種情況沒有考慮到位,都會造成題目分析的失準.為了避免這種現象的出現,就要及時引入分類的思想方法.
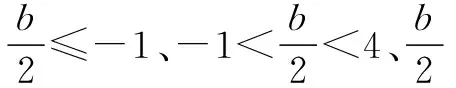
分類思想方法的運用并不是隨意為之的.想要將每一種問題可能性考慮全面,且恰到好處,學生們必須對當前知識內容形成準確認知,細致分析問題,找到分類的標準所在,方能使得分類的過程清晰明確.
三、探尋化歸思想方法,靈活巧妙完成解題
在面對一些疑難復雜問題時,學生們經常會感到,直接切入進行分析是行不通的.這時,就需要讓大家建立起一種化歸的意識,善于將難于分析的問題轉化為所熟知的內容,在不斷替代與移轉的過程中完成分析解答.
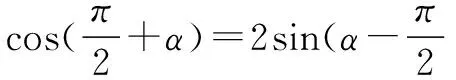
相比于前面幾種思想方法來講,化歸的思想方法表現得較為抽象.它既可以體現在實際的題目計算環節中,也可以運用在抽象的思維分析環節里.化歸的意識就像是在已知與未知之間搭建起了一座橋,讓學生們的思路更加順暢,解題更加輕松.
[1]黃旺叢.高中數學問題解決教學模式探究[J]. 考試周刊,2016(03)
G632
B
1008-0333(2017)09-0018-01

