一種旋翼無人機組合導航系統設計及應用*

劉洪劍，王耀南*，譚建豪，李樹帥，鐘 杭

(1.湖南大學電氣與信息工程學院，長沙410082;2.機器人視覺感知與控制技術國家工程實驗室，長沙410082)

一種旋翼無人機組合導航系統設計及應用*

劉洪劍1，2，王耀南1，2*，譚建豪1，2，李樹帥1，2，鐘 杭1，2

(1.湖南大學電氣與信息工程學院，長沙410082;2.機器人視覺感知與控制技術國家工程實驗室，長沙410082)

針對傳統組合導航算法相對復雜，對系統硬件要求太高，實時性不好的缺點，設計了一種基于線性卡爾曼濾波器的簡單實用組合導航算法。考慮到傳統卡爾曼濾波器在系統噪聲變化時濾波精度變差甚至發散以及模糊控制器計算量大的缺陷，設計了線性迭代調整觀測噪聲參數的方法對濾波器進行自適應改進，提高了算法的魯棒性和實時性。利用STM32微控制器和MEMS慣性單元以及UBLOX GPS定位模塊搭建硬件平臺進行實驗驗證。結果表明:在168 MHz時鐘頻率下，一次姿態數據讀取和解算共耗時3.27 ms，一次組合導航濾波耗時2.18 ms，二者分別運行在100 Hz和5 Hz頻率下。最終組合導航結果可以滿足無人機在1 m的精度范圍內自動懸停的需求，驗證了所設計的組合導航算法的可靠性和實用性。

無人機;卡爾曼濾波;自適應;組合導航

如今旋翼無人機已經成為一個研究熱點，位姿信息獲取及位姿控制是無人機自主式飛行面臨的基本問題。目前旋翼無人機的姿態解算及控制研究已經比較成熟，而導航控制問題仍處于研究階段。相比于傳統監測等飛行任務，本課題研究的面向任務的旋翼飛行機械臂自主作業與控制系統則需要更加準確的位置信息，以實現無人機懸停模式下準確的空中抓取作業［1］。

應用于旋翼無人機上集加速度計和陀螺儀于一體的微型慣性測量單元(MIMU)，不僅可以通過姿態解算得到姿態信息。還可以作為慣性導航系統(INS)，提供自主式無人機導航與制導所需的位置信息。但是其導航誤差會隨時間快速積累，不能單獨用于長時間位置導航。在室外環境下，GPS能提供準確的位置信息，但是其測量誤差不可避免，短時間測量精度較差。INS和GPS各有所長，優勢互補，利用卡爾曼濾波器對INS與GPS數據進行融合，獲得導航參數的最優估計值，可以得到高精度、高可靠的導航信息［2］。

目前對基于卡爾曼濾波器的組合導航算法的研究已有很多［3－4］。主要研究熱點集中在針對系統模型非線性或系統噪聲統計特性不明確引起的濾波器精度降低甚至發散這一問題的改進上。具體改進措施有:針對系統非線性模型的擴展卡爾曼濾波(EKF)算法［5－6］、粒子濾波(PF)算法［7－8］和無跡卡爾曼濾波(UKF)算法［9－11］等;針對系統噪聲不確定性的自適應衰減記憶法卡爾曼濾波算法［12］、Sage-Husa自適應卡爾曼濾波算法［13－14］、模糊邏輯自適應卡爾曼濾波算法［15－16］等。

EKF算法將非線性函數直接忽略高階項進行線性化，勢必存在高階項截斷誤差，而且雅可比矩陣求解的計算量比較大。PF算法大量粒子的隨機產生，很難滿足導航系統實時性需求。UKF算法對初始值的取值比較敏感，系統噪聲不確定性會對濾波精度產生較大的影響;目前對于記憶衰減因子的選擇沒有完善的理論，只能根據經驗進行確定。Sage-Husa自適應算法可以在一定程度上降低模型誤差、提高濾波精度，但是計算量大，且對于階次較高的系統可靠性不高。模糊邏輯的思想和其他自適應方法是一致的，都是用權值調整噪聲參數。但是模糊邏輯將調整過程根據經驗分為幾個模糊空間，而其他方法可以在每一點上調整，所以模糊邏輯調整的精確性不如其他方法好。而且模糊控制作為一種人工智能技術，對系統硬件要求比較高。

以上方法雖在精度上都達到了較理想的效果，但是一個共同的缺點就是算法復雜導致實時性不理想，對系統硬件要求太高，嚴重限制了其在實際中的應用，大部分算法只能停留在仿真階段。本文從工程應用角度出發，提出一種簡潔有效的實時自適應卡爾曼濾波算法。首先設計INS/GPS組合導航系統模型框架，然后建立線性系統的離散卡爾曼濾波模型。使用線性迭代的方式代替模糊控制器來克服系統噪聲的不確實性。最后設計實驗平臺對算法進行驗證并得出結論。

1 組合導航系統模型設計

INS/GPS組合導航系統一般有兩種信息融合方式:速度、位置組合(松耦合)和偽距、偽距率組合(緊耦合)，本文采用前一種方式，這種方法的測量模型是線性的，可以用標準卡爾曼濾波器進行信息的融合。

設計的INS/GPS組合導航系統框圖如圖1所示。慣性導航系統(INS)以牛頓力學為基礎，首先由姿態解算得到姿態矩陣Tnb，建立起導航坐標系。然后利用加速度計來測量無人機的實時加速度，將實時加速度通過Tnb轉換到導航坐標系中，經過一次積分運算得到實時速度，再一次積分運算得出實時位置。然后利用自適應卡爾曼濾波器結合GPS提供的速度和位置信息對上述預測值進行校正。這里采用輸出校正法，利用估計值直接校正組合導航系統最終輸出的速度和位置，工程上實現簡單。

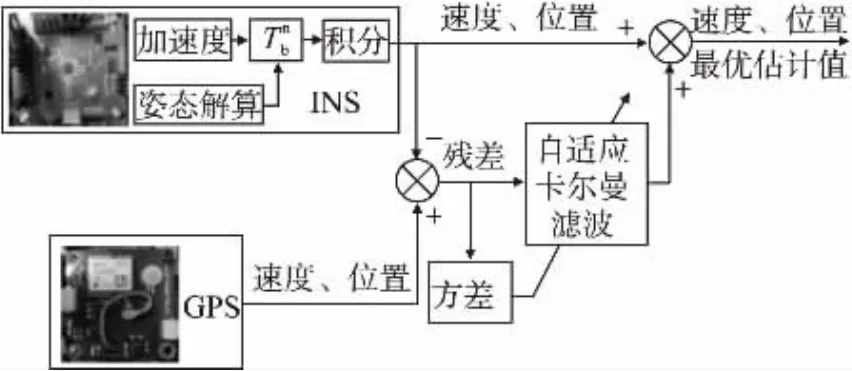
圖1 組合導航系統框圖

圖1中INS為公共子系統，GPS為輔助子系統。兩個子系統分別進行定位運算，然后將兩者結果融合到一起。該算法的好處是:不需對子系統內部做任何改動，方便系統集成，比如在不方便使用GPS的情況下，可以使用其他定位系統如視覺傳感器直接替換掉GPS模塊，而程序不需做太大的改動。而且姿態解算是組合導航的基礎，雖然兩個過程同時進行，但是組合導航算法不會對姿態算法產生任何影響。

為了充分發揮慣性傳感器更新速率快的優勢，INS子系統運行在100 Hz的高頻率上，而組合導航卡爾曼濾波器運行在5 Hz的GPS低定位頻率上。當GPS出現故障時，系統可以直接輸出INS子系統的定位結果，在短時間內可提供較準確的位置信息。

2 卡爾曼濾波器設計

步驟1 狀態空間表達式的建立

旋翼無人機的運行狀態可以用精簡的6個狀態變量來描述:3個速度分量和3個位置分量。為了簡化計算量，本文選取狀態向量為:

式中:vn，ve，vd分別表示北東地方向的速度分量，pn，pe，pd分別北東地方向的位置分量。則可以建立系統的狀態方程:

式中:Tnb為已知的機體坐標系b到導航坐標系n的姿態矩陣:

dT為卡爾曼濾波周期，［dvx，dvy，dvz］T表示周期dT內無人機在機體坐標系b中測得的速度增量。由于慣導系統數據更新速率比GPS模塊數據更新速率要快得多，而且在GPS數據更新時間間隔內，系統加速度不可能為一定值。為減小狀態預測誤差，本文采用在GPS更新周期內對加速度計多次采樣求積分的方式得到速度增量:

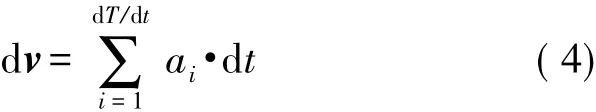
式中:dt表示INS的更新周期。G表示導航坐標系n中的重力加速度值。過程噪聲ωk=［ωdvx，ωdvy，ωdvz］T。

取GPS模塊輸出的速度和位置信息作為觀測變量，則系統觀測向量為:

觀測方程為:

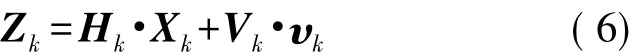
測量噪聲υk=［υvn，υve，υvd，υpn，υpe，υpd］T。

到此，建立了系統的線性離散狀態空間模型。

步驟2 濾波條件的建立

將式(2)寫成線性離散狀態方程的形式:

式中:“(－)”表示對應量的預測值，“(+)”表示對應量的估計值，下文表示方法類似。則系統一步狀態轉移矩陣和過程噪聲分布矩陣分別為:

式中:I3×3表示3×3的單位矩陣，03×3表示3×3的0矩陣，下文表示方法類似。

將狀態向量Xk代入式(6)觀測方程，可知輸出矩陣和觀測噪聲分布矩陣分別為:

卡爾曼濾波器是一個循環迭代過程，迭代需要一個初始條件。本文以無人機起飛點處作為位置坐標原點，為了讓濾波器盡快收斂，此處初始條件設為:

為了簡化模型，通常我們假設過程噪聲ωk和觀測噪聲υk為零均值高斯白噪聲，且其統計特性不隨時間和環境而改變:

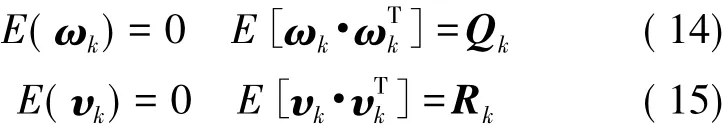
過程噪聲協方差矩陣Qk和觀測噪聲協方差矩陣Rk分別代表了預測的不確定性和測量的不確定性。即使在上述假設成立的條件下，其值也是無法直接測量或者根據先驗知識得到的，需要在實際應用時根據濾波效果不斷調整得到一個合理值。根據本文調試經驗，可初步設定:

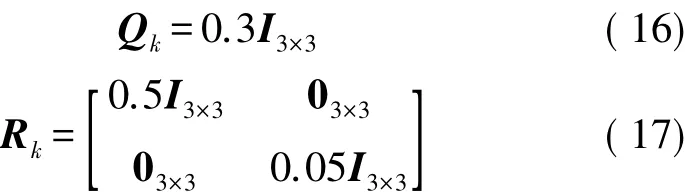
步驟3 濾波器的運行

利用式(7)～式(17)，可以建立系統的卡爾曼濾波模型如下:

狀態預測:

協方差預測:

卡爾曼增益:

狀態修正:

協方差修正:

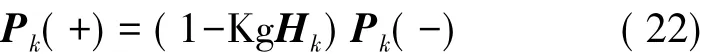
3 測量噪聲自適應調整

對由式(2)和式(6)描述的系統，卡爾曼濾波器給出了最小協方差意義下狀態向量的最優無偏估計。但是在實際中，過程噪聲、測量噪聲以及殘差一般情況下不再是高斯白噪聲［12，17］，此時用傳統的卡爾曼濾波器很容易導致濾波發散，一旦產生發散則信息融合失敗。

通常的解決方法是通過殘差方差匹配技術，使濾波器根據環境的改變自適應調整統計參數，增強殘差的理論協方差陣與實際協方差陣的一致性［17］。文獻［14，17］介紹的方法都是通過模糊控制器來實現的。雖然仿真效果都不錯，但是進行模糊化、模糊推理和去模糊化等復雜過程嚴重影響了實際應用時算法的實時性。所以本文設計如下的線性迭代自適應過程:

定義殘差為:

殘差的理論協方差陣計算公式［17］:

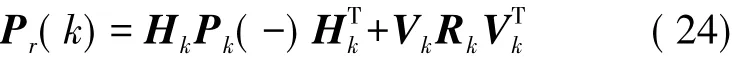
實際協方差陣計算公式:

式中:N為用來計算實際協方差陣窗口的大小，N取值過大會影響自適應調整的實時性，取值過小會降低Cr(k)的準確性，都不利于自適應性能的改善。根據調試結果，本系統取5＜N＜30較合適，本文取N=10進行實驗。

從式(24)可以看出，改變觀測噪聲協方差陣Rk的大小，可以改變殘差協方差的理論值Pr(k)。所以可以通過調整Rk來改變Pr(k)從而增強Pr(k)與Cr(k)的一致性。

用式(26)來表示理論值與實際值的一致程度:

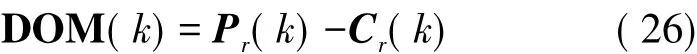
設計Rk的線性迭代調整公式為:

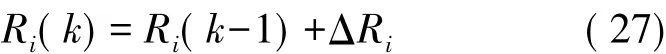
式中:Ri(k)表示Rk主對角線上第i個元素。則根據上述分析可得如下關系:若DOMi(k)＞0，即理論值大于實際值，應減小Ri(k)，所以ΔRi＜0;若DOMi(k)=0，即理論值等于實際值，保持Ri(k)不變，所以ΔRi=0;若DOMi(k)＜0，即理論值小于實際值，應增大Ri(k)，所以ΔRi＞0。

|ΔRi|的大小可根據實際情況進行調整。取得太大，Rk的調整力度過大導致震蕩;取得太小，Rk的自適應調整效果不明顯，退化為常規卡爾曼濾波。一般可以參考式(17)，取Ri(k)×10－1數量級合適。如需進一步提高自適應性能，可以根據DOM(k)的大小，自動調整|ΔRi|，使兩者成正向關關系，但是參數整定過程會變得繁瑣。權衡利弊本文取:

進行參數自適應調整后，卡爾曼濾波器具體步驟需要進行修改，在上述濾波模型后面需加上如下步驟:① 計算式(20)時輸出式(24)，得到Pr(k);②計算式(21)時輸出式(23)，得到rk;③將rk代入式(25)，得到 Cr(k);④將Pr(k)和Cr(k)代入式(26)，得到DOM(k);⑤根據DOMi(k)求ΔRi;⑥將ΔRi代入式(27)，求得Rk作為下一次濾波迭代中式(20)的噪聲參數。

圖2 無人機實驗平臺

4 實驗結果及分析

4.1 實驗平臺

圖2為本文設計的無人機實驗平臺，軸距60 cm。飛行控制器采用STM32F405(Cortex－M4內核)為中央處理器，工作頻率168 MHz。主要完成傳感器數據采集、姿態解算、組合導航、實驗數據傳送、控制量輸出等功能。慣性測量單元(IMU)MPU6050固連于載體上，該芯片內置一個三軸陀螺儀和一個三軸加速度計，實驗使用±2 000(°)/s和±2 gn的量程，16 bit數字輸出，采樣數據最高輸出速率可達1 kHz。GPS接收機使用UBLOX NEO－M8N定位模塊，該模塊定位精度PDOP數值能達到2.0 m左右。采用NMEA－0183協議通過串口輸出GPS定位數據，并可通過UBX協議對模塊進行配置。NMEA－0183協議利用ASCⅡ碼傳遞GPS定位數據，一幀的最大長度可達600 byte左右，數據量比較大。為了數據傳輸的穩定性和快速性，本設計使用主控制器的DMA串口功能接收GPS數據。模塊最高更新頻率可達到10 Hz，但數據不夠穩定，故本文使用5 Hz更新頻率。經測試，一次姿態解算耗時約3.27 ms，一次組合導航濾波耗時2.18 ms，為留冗余，設計姿態解算頻率為100 Hz。即每10 ms進行一次姿態解算和INS導航，每200 ms進行一次GPS數據讀取和位置卡爾曼濾波計算。

4.2 實驗測試與結果分析

使用搭建的硬件平臺對算法進行實驗驗證，通過無線串口模塊將數據實時傳送到電腦端得到測試數據。實驗結果如圖3～圖11所示。其中，圖3～圖8為靜態濾波結果圖，即電機靜止狀態下，手持無人機在水平面內快速移動時的位置濾波結果。圖9～圖11為動態濾波結果圖，實驗中給定無人機一個三維路徑，在其自動飛行的過程中，實時傳回濾波數據。

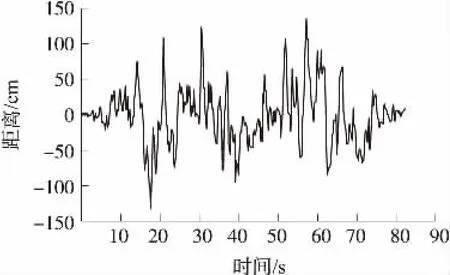
圖3 靜態東向位置殘差曲線

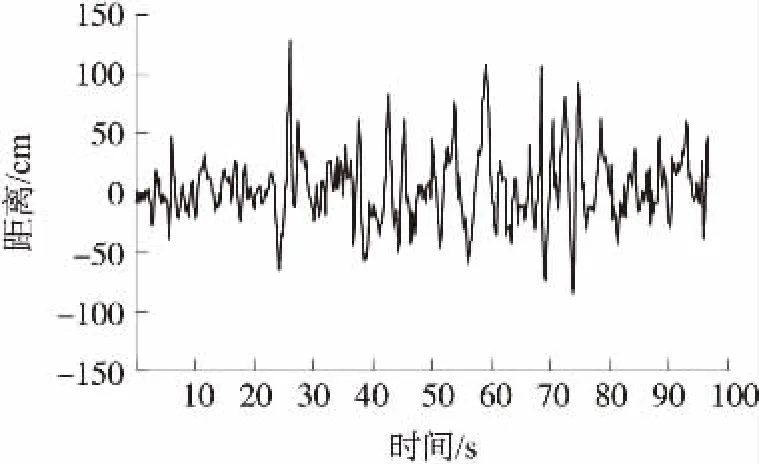
圖4 靜態北向位置殘差曲線

由圖3和圖4位置濾波的殘差曲線可以看出，整個實驗過程，殘差一直保持著0均值白噪聲特性不變。系統穩定后，殘差最大值小于1.5 m。圖5和圖6分別表示東向和北向位置濾波的殘差協方差曲線，實線表示實際值，虛線表示理論值。結果顯示，測量噪聲Rk的自適應調整，使殘差協方差的理論值緊跟實際值變化，提高了濾波器在系統噪聲統計特性改變時的濾波精度。圖7和圖8中實線和虛線分別表示靜態位置濾波曲線的測量值和估計值，可以看出，濾波器對GPS的輸出數據起到了良好的平滑和跟蹤效果。為了更好地驗證算法的實際應用效果，使用最優估計值對無人機進行定位實驗。

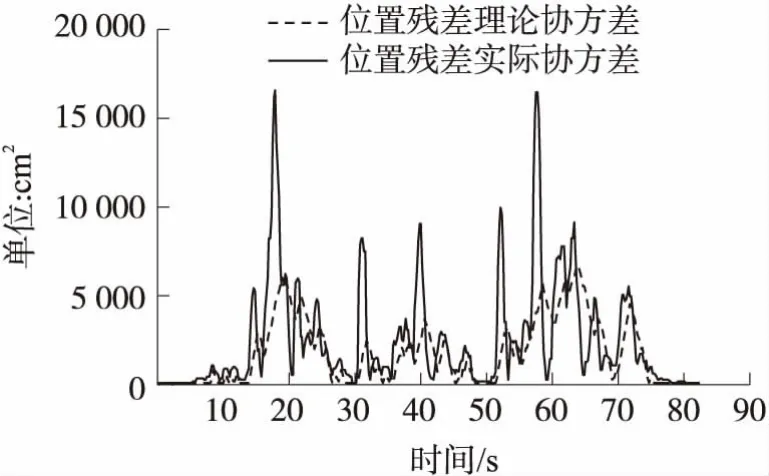
圖5 靜態東向位置殘差協方差曲線

圖6 靜態北向位置殘差協方差曲線

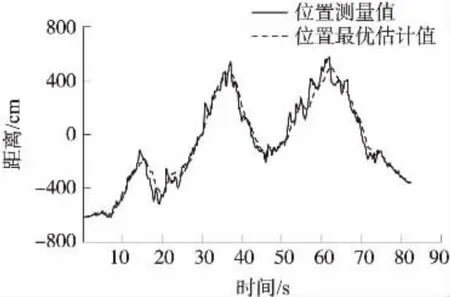
圖7 靜態東向位置濾波曲線

圖8 靜態北向位置濾波曲線

圖9和圖10的實驗結果證明，無人機可以平穩地執行起飛、按軌跡飛行、懸停和降落等任務，動態濾波殘差在1.5 m以內。以圖11所示的視角觀察無人機的懸停效果和漂移范圍，結果顯示，在風力較小的環境下，無人機的空間位置漂移范圍可在1 m以內。

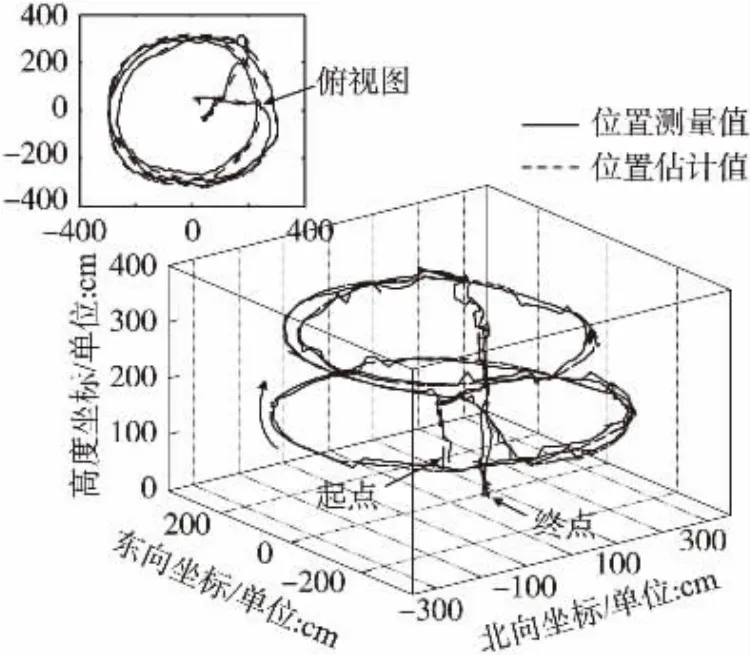
圖9 動態三維位置濾波曲線

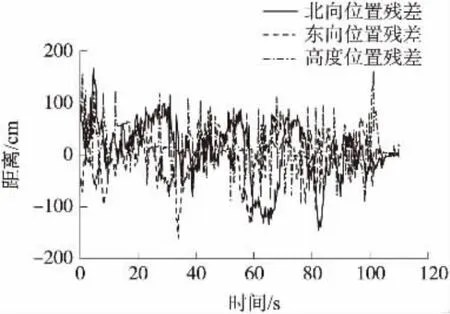
圖10 動態三維位置殘差曲線

圖11 無人機組合導航自動懸停實驗

5 結束語

本文首先建立了組合導航系統模型，然后按照模型的思路，選取了精簡的6個狀態變量設計出系統線性離散卡爾曼濾波器。不僅避免了系統的非線性帶來的問題，也減少了計算量，保證了算法的實時性要求。為克服系統噪聲統計特性的不確定性給濾波器帶來的負面影響，對系統測量噪聲進行了自適應調整。使用線性迭代的方式代替模糊控制器，思路簡單且易于實現。最后設計并制作了實驗驗證平臺，結果證明，利用濾波器輸出的最優位置估計信息，無人機可以實現長時間的穩定自動懸停，精度在1 m以內。說明本系統可以為無人機在室外環境下的自主作業與控制提供準確有效的位置信息。

［1］ 譚建豪，王耀南，王媛媛，等.旋翼飛行機器人研究進展［J］.控制理論與應用，2015，32(10):1278－1286.

［2］ 董緒榮，張守信，華仲春.GPS/INS組合導航定位及其應用［M］.北京:國防科技大學出版社，1998.

［3］ 秦永元，張洪鉞，汪叔華.卡爾曼濾波與組合導航系統原理［M］.西安:西北工業大學出版社，1998.

［4］ 董健康，安東.自適應卡爾曼濾波在組合導航中的應用研究［J］.計算機技術與發展，2011，21(10):183－185.

［5］ 張品秀，黃操軍，喬相偉.基于自適應擴展Kalman濾波的SINS/GPS深組合研究［J］.傳感技術學報，2010，23(3):408－412.

［6］ Psiaki M L.The Super-Iterated Extended Kalman Filter［C］// AIAA Guidance，Navigation，and Control Conference，2004(8): AIAA－04－5418.

［7］ Rigatos G G.Nonlinear Kalman Filters and Particle Filters for integrated Navigation of Unmanned Aerial Vehicles［J］.Robotics and Autonomous Systems，2012，60(7):978－995.

［8］ 陳延軍，梁新華，潘泉，等.兩級量測更新的粒子濾波檢測前跟蹤算法［J］.傳感技術學報，2015，28(1):115－120.

［9］ 楊波，秦永元，柴艷.UKF在INS/GPS直接法卡爾曼濾波中的應用［J］.傳感技術學報，2007，20(4):842－846.

［11］歐縣華，武憲青，何熊熊.基于AIUKF的WSN節點定位算法［J］.傳感技術學報，2015，28(2):234－238.

［12］馬忠孝，劉宗玉，陳明.基于模糊邏輯的自適應卡爾曼濾波在GPS/INS組合導航中的應用［J］.信息與控制，2006，35(4): 457－461.

［13］王沖，曾慶軍.基于Sage-Husa自適應濾波算法的AUV組合導航系統設計［J］.電子設計工程，2013，21(15):75－77.

［14］張少軍，王宏麗，蔡宗平.MIMU/GPS組合導航模糊自適應卡爾曼濾波研究［J］.電光與控制，2008，15(8):84－86.

［15］Sasiadek J Z，Wang Q，Zeremba M B.Fuzzy Adaptive Kalman Filtering For INS/GPS Data Fusion［C］//Proceedings of the 15th IEEE International Symposium on Intelligent Control.［s.l.］:［s.n.］.2000:181－186.

［16］段宇，徐曉蘇.模糊邏輯自適應卡爾曼濾波技術在GPS/INS組合導航系統中的仿真研究［J］.傳感技術學報，2003，16(2): 165－169.

［17］柏菁，劉建業，袁信.模糊自適應卡爾曼濾波技術研究［J］.信息與控制，2002，31(3):193－197.

劉洪劍(1991－)，男，湖南大學電氣與信息工程學院碩士研究生，主要研究方向為無人機數據融合與控制，hnlhj @hnu.edu.cn;

王耀南(1957－)，男，湖南大學教授，博士生導師，主要研究方向為智能控制理論與智能信息處理，yaonan@hnu.edu.cn。

A Kind of Design and Application of Integrated Navigation Systems for UAVs*

LIU Hongjian1，2，WANG Yaonan1，2*，TAN Jianhao1，2，LI Shushuai1，2，ZHONG Hang1，2
(1.College of Electrical and Information Engineering，Hunan University，Changsha410082，China; 2.National Engineering Laboratory for Robot Visual Perception and Control Technology，Changsha410082，China)

Aiming at the disadvantages that the traditional integrated navigation algorithm has high complexity，high hardware requirements，and poor real-time performance，a simple and practical integrated navigation algorithm based on linear Kalman filter is designed.Considering the problems that the filtering accuracy will become terrible or even divergence when the system noise varies，and great computational burden of the fuzzy controller，a method to adjust observation noise parameters adaptively based on linear iteration is proposed to improve the adaptive performance and robustness of the filter.Then，the proposed method is verified in an experimental system that consists of the STM32 microcontroller，the MEMS inertial unit and the UBLOX GPS positioning module.The experimental results indicate that，the time of reading attitude data and attitude solution costs 3.27 ms in total running at 100 Hz，and the time of integrated navigation filtering costs 2.18 ms in total running at 5 Hz，both under 168 MHz clock frequency.The final integrated navigation results can meet the needs of the UAVs automatic hover in the precision of 1 m and verify the reliability and practicability of the designed integrated navigation algorithm.

UAV;Kalman filter;self-adaptive;integrated navigation

U666.11

A

1004－1699(2017)02－0331－06

C:6140B;6330;7220

10.3969/j.issn.1004－1699.2017.02.028

項目來源:國家自然科學基金重點項目(61433016);國家自然科學基金面上項目(61573134)

2016－07－03 修改日期:2016－09－06