一種基于電磁感應原理的角位移參數測量方法

武 丹，李 劍，韓 焱

(中北大學信息探測與處理技術研究所山西省重點實驗室，太原030051)

一種基于電磁感應原理的角位移參數測量方法

武 丹*，李 劍，韓 焱

(中北大學信息探測與處理技術研究所山西省重點實驗室，太原030051)

針對目前常規彈藥彈體研究領域角位移參數大動態和高精度的測量需求，提出了一種基于電磁感應原理的角位移參數測量方法，并設計了相應的角位移傳感器。采用感應線圈獲取彈體大轉速動態范圍內切割地磁場的信息，通過邊沿檢測和脈沖計數相結合的自適應閉環頻率跟蹤測量算法測量彈體旋轉過程中的實時角位移參數信息，并采用周期清零的方式，消除累積誤差。半實物和實物仿真試驗結果表明:該角位移傳感器不僅能夠測量大動態范圍內的角位移，拓寬測量范圍從600°/s～36 000°/s，而且完全消除了測量過程中的累積誤差。測量誤差小于0.220%，累加誤差最大只有0.2°/s，實現了對彈藥彈體角位移參數的實時、高精度測量，在姿態測量和地磁導航等應用領域具有一定的工程應用價值。

角位移;自適應閉環頻率跟蹤測量;電磁感應;FPGA

常規彈藥彈體的精確制導化是國際武器彈藥研究領域的一個研究熱點，其中，彈藥彈體飛行過程中的角運動參數(如角速率和角位移)，是一項直接關系到其制導精度的關鍵參數之一，從角運動參數信息中可以間接獲得彈藥彈體的運動姿態信息，從而為姿態解算、導航解算等應用領域提供有效的輸入、輸出參數。目前，科研工作人員提出了很多新型的角位移測量方法，主要分為光學測量和非光學測量兩種。光學測量有光纖角位移傳感器和利用激光測角器、點衍射干涉法的角位移測量方式等等，主要特點是針對目標體的角位移狀態進行非接觸式測量［1－6］;非光學測量有電感式角位移傳感器、基于ELC的角位移傳感器和基于脈寬調制(PWM)信號電壓的測量方法等，大多是針對電子設備和多種工業場合的應用［7－14］。這些測量方法雖然對角位移的測量都達到了一定的精度，但是都存在測量動態范圍不大的缺點。較為傳統的角位移測量方法是利用MEMS陀螺儀，而在測量過程中存在的累積誤差常常會造成對角位移測量結果的精度不高［15－17］。針對上述問題，同時針對常規彈藥彈體角位移參數高效、高精度和大動態的應用需求，本文提出了一種基于電磁感應原理的角位移參數測量方法，并設計得到了一種角位移傳感器。通過感應線圈獲取彈藥彈體大轉速范圍內切割地磁場的信息，采用自適應閉環頻率跟蹤測量算法測量對應旋轉狀態下的角位移參數，并每周期進行刷新清零，消除角位移測量過程中的累積誤差，從而實現對彈藥彈體角位移參數的實時、高精度測量，在姿態測量和地磁導航等應用領域具有一定的工程應用價值。

1 傳感器的測量原理

本文采用電磁感應線圈獲取彈體旋轉時實時切割地磁場的角運動信息，通過自適應閉環頻率跟蹤測量算法將該信息轉換為彈體旋轉時的角位移信息。

在不同轉速條件下，電磁感應線圈切割地磁場，通過線圈磁通量的不同使得產生的感應電動勢不同。線圈旋轉運動產生感應電動勢為:

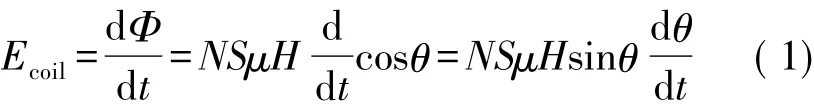
式中:Ф為通過線圈的磁通量;t為時間;N為固定的線圈匝數;S為線圈橫截面積;μ為線圈芯子磁導率;H為磁場強度。由于在一定的設計規則下，N、S、μ是由線圈本身特性決定的，且H是確定的常量，故令A=NSμH。同時令線圈的角速率則上式可變為:

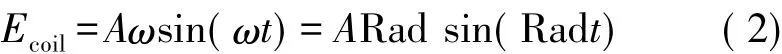
從式(2)中可以看出，當線圈的角速率(即旋轉角頻率)一定時，線圈輸出信號為標準正弦波。感應電動勢Ecoil與旋轉頻率Rad之間表現出一一對應的線性正比關系，正弦信號的角頻率就代表了彈藥彈體的旋轉角速率。

自適應閉環頻率跟蹤測量算法是在利用電壓頻率轉換器(VFC)和數模轉換器(DAC)構成頻率測量單元的基礎上，通過邊沿檢測和脈沖計數相結合的方式，調節DAC的輸出電壓值V控制VFC改變輸出所對應的振蕩脈沖頻率，保證彈體從參考零位脈沖刷新旋轉1/2周期內，使VFC自適應輸出N個脈沖;以計數半周期脈沖個數的方式，通過閉環調節，保證每半周期脈沖計數值均為N，并以脈沖累加步進的方式形成鋸齒波來輸出角位移參數信息。鋸齒波的幅值就代表了彈體的角位移信息。本文提出的自適應閉環頻率跟蹤測量算法是一種滯后算法，其測量得到的角位移參數信息要比彈體實際的旋轉狀態晚一個周期，其測量原理如圖1所示。

設半周期記錄VFC的輸出脈沖個數為N，DAC的初始輸出電壓值為V1，VFC輸出頻率為f1。彈體在當前周期內半周期計數脈沖值為M時，DAC的輸出電壓值調節為V2，VFC對應的輸出頻率變為f2，則f2和f1之間的頻率依賴關系為:

輸出DAC的輸出信號即為角位移的輸出鋸齒波，如圖2所示，鋸齒波的累加形成以VFC產生的振蕩脈沖為更新標志。結合圖1，參考零位脈沖刷新，DAC從0 V開始以VFC的脈沖頻率累加步進，半個周期自適應計滿N個脈沖時達到預設的輸出幅值，這樣，第1個鋸齒波就代表彈體的旋轉角位移為(0°～180°)+n·360°，第2個鋸齒波就代表彈體的旋轉角位移為(180°～360°)+n·360°。

由于彈體的角位移與鋸齒波輸出電壓呈一定的線性正比關系，根據VFC的輸出特性方程(4)，可得DAC的輸出調節電壓值V2為式(5)，從而可以獲得彈體實時的旋轉角位移Dis為式(6)。

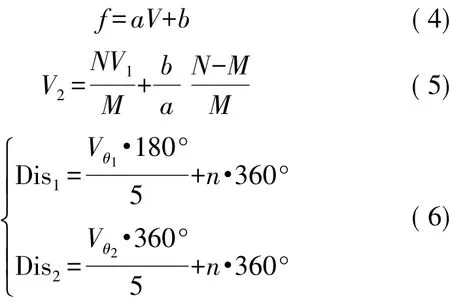
式中:n=0，1，2，…，表示彈體的旋轉周期。結合式(4)～式(6)可知Dis=f(V1，M，N)，可以看出，角位移的測量精度與彈體上一周期的DAC調節電壓值V1和半周期的計數值M有關，而DAC輸出精度取決于DAC本身的量化位數，且計數值M是周期性歸零重新計數，消除了長時間累加計數的誤差，因此本系統不存在陀螺儀的累積誤差。

圖1 傳感器測量原理波形示意圖

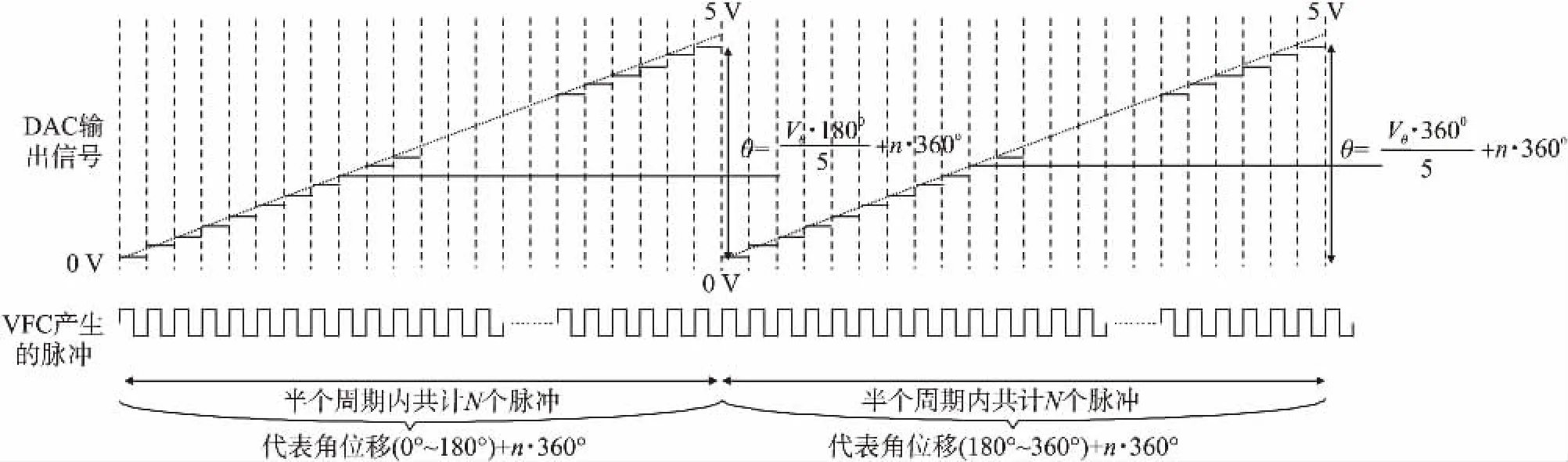
圖2 角位移輸出波形示意圖

2 傳感器的系統設計

2.1 電磁感應線圈

采用電磁感應線圈獲取彈體不同轉速條件下切割地磁場的信息。根據法拉第電磁感應原理，在線圈線徑0.09 mm、匝數9500匝、線圈電阻約665 Ω的設計規則下，對繞制的單軸線圈進行標定，其測試頻率與輸出電壓之間的關系如表1所示。

通過線性擬合的方式對感應線圈的線性度進行標定，得到其輸出線性曲線與擬合曲線，如圖3所示。

結合圖3和表1可知，采用感應線圈切割一個固定磁場時，感應磁信號的頻率在4 Hz～100 Hz的范圍內，切割頻率和產生的感應電壓呈線性關系，線性度為0.5%FS，滿足彈藥彈體大動態范圍的測量要求。

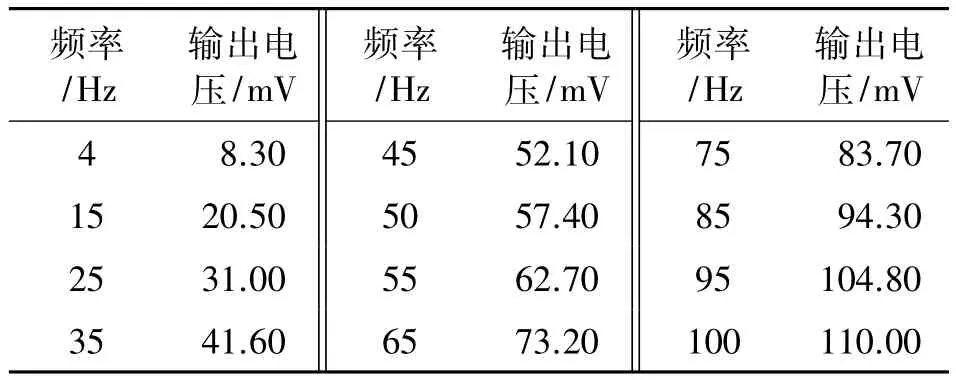
表1 線圈輸出信號頻率－電壓關系表

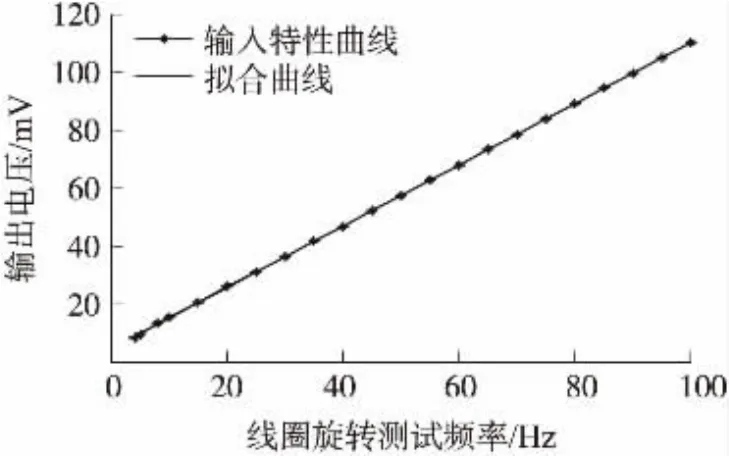
圖3 線圈輸出特性曲線圖

2.2 自適應閉環頻率跟蹤測量算法

采用FPGA作為控制核心實現自適應閉環頻率跟蹤測量算法，其實現過程如圖4所示。

步驟1 將感應線圈采集到的地磁信號經調理整形輸入至FPGA;

步驟2 通過邊沿檢測單元檢測整形后信號的上升沿和下降沿，利用上升沿對VFC輸出的脈沖進行清零同時確定脈沖計數的起點并重新開始計數，當下降沿到來時，計數結束，并將計數值鎖存，設鎖存值為M;

步驟3 通過式(5)構建角位移測量模型，得到DAC調節電壓，并在下一個上升沿到來時更新閉環DAC，進一步控制VFC改變輸出所對應的脈沖頻率，以“閉環”調節模式對獲得的信號進行實時的修正校準，輸出DAC輸出的鋸齒波就代表了彈體上一周期的角位移信息，至此完成對角位移參數的測量。

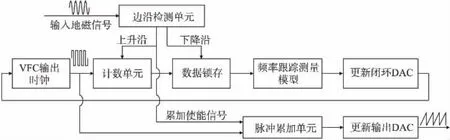
圖4 角位移參數測量過程設計框圖

3 試驗驗證

3.1 角位移累加誤差計算

精度是衡量角位移參數測量的重要指標，如圖5所示，為1 s內角位移累加誤差計算流程圖。

通過多路數采系統和上位機采集卡采集傳感器輸出的信號并利用MATLAB進行角位移累加計算，通過數據導入、峰值讀取、建立矩陣、線性插值和尋找最優點的方式，完成對角位移參數累加誤差的計算。

圖5 角位移參數累加誤差計算流程圖

3.2 實物試驗——三軸飛行轉臺

為了驗證所設計角位移傳感器的原理正確性和實際可利用性，利用三軸位置速率搖擺溫控轉臺進行了三軸飛行轉臺測試試驗，如圖6所示，將本系統研制的傳感器固定在轉臺的軸心處，控制轉臺旋轉偏移30°，設置半周期計數脈沖值為1 024，即N=1 024，改變轉臺內框的旋轉測試頻率。

圖6 三軸飛行轉臺實驗測試平臺

如圖7所示，為轉臺在內框旋轉測試頻率為1 000°/s時的輸出信號波形圖。

圖7 1 000°/s轉臺頻率下的輸出信號波形圖

從圖7中可以看出，當轉臺旋轉測試頻率為1 000°/s時，參考零位脈沖的頻率穩定在 2.770 Hz，說明本傳感器在測量過程中能夠準確地檢測到每周期的初始零點并實現自動清零，數據更新率高。同時可以清楚地看到傳感器輸出鋸齒波穩定，其初始零點與參考零位脈沖一一對應，且閉環調節DAC的輸出電壓穩定，紋波小，說明傳感器性能穩定，測量的角位移準確。

對轉臺旋轉頻率1 000°/s時對應的傳感器輸出信號進行誤差累加分析，得到角位移累加結果，如圖8所示。

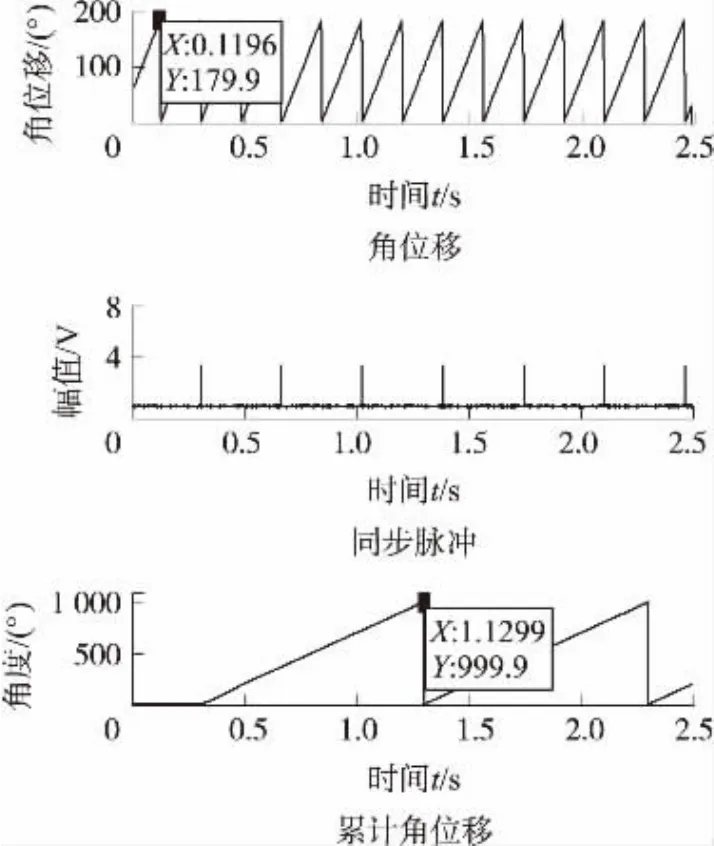
圖8 1 000°/s時角位移累加計算圖

從圖8中可以看到通過累加計算，在轉臺旋轉頻率為1 000°/s時，傳感器測量得到的角位移信息(輸出鋸齒波)在1 s中累加999.9°，誤差為0.1°，傳感器測量精度高，準確度高。

改變三軸轉臺的內框旋轉頻率，得到如表2所示的實驗測試結果。

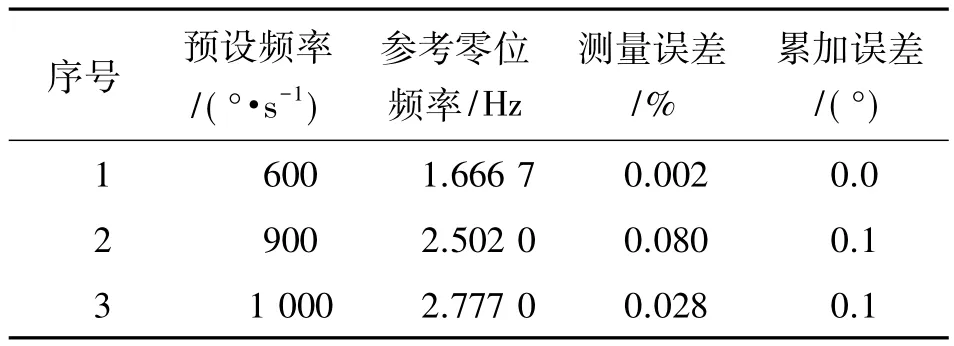
表2 三軸飛行轉臺實驗測試結果

由表2可知，當轉臺內框以600、900和1 000°/s (相當于彈體的實際旋轉頻率為1.6667、2.500 0和2.777 8 Hz)的預設旋轉角頻率進行試驗時，通過傳感器測量獲得的角位移精度很高，測量誤差最大為0.080%，最小為0.002%，累加結果顯示在1 s內測量精度最大只有0.1°的誤差，表明角位移傳感器的低頻測量分辨率高，穩定性能好。

3.3 半實物試驗——交變磁場

為了驗證傳感器在實際工況中大動態范圍內的適用性，采用磁屏蔽筒和亥姆霍茲線圈式模擬交變磁場發生器進行仿真實驗。如圖9所示，將角位移傳感器放置在亥姆霍茲線圈式模擬交變磁場中，固定臺面傾斜角30°，設置磁場信號發生器的頻率(即實際工況下彈體的轉速頻率)為5 Hz～100 Hz，磁場強度為±1 Gauss。如圖10所示，為傳感器在100 Hz磁場交變頻率下的輸出信號波形圖。

圖9 模擬交變磁場實驗測試平臺

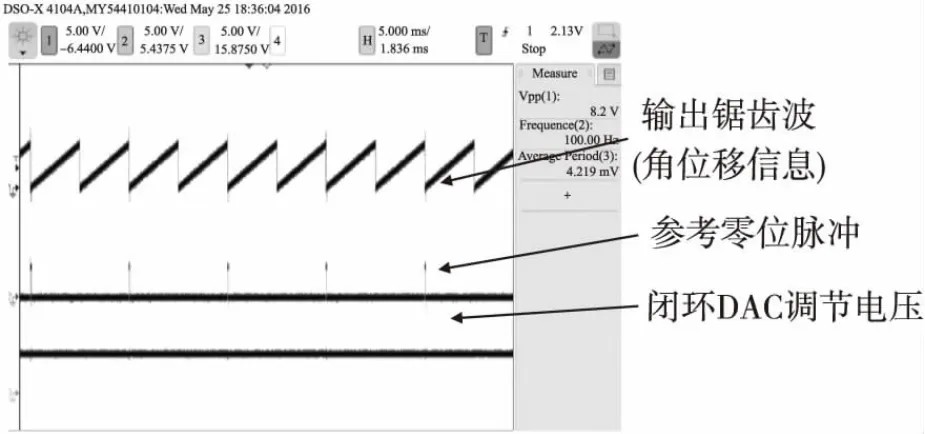
圖10 磁場交變頻率100 Hz下的輸出信號波形圖

磁場交變頻率改變，得到角位移參數的測量結果和誤差分析結果，如表3所示。

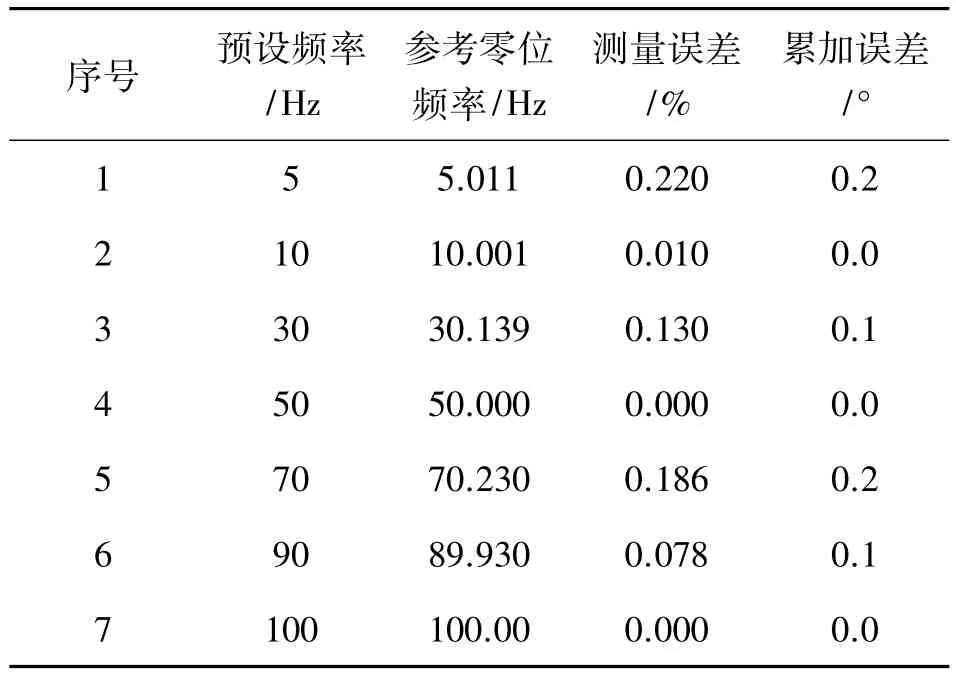
表3 交變磁場實驗測量結果

從表3中可以看出，隨著磁場預設交變頻率的改變，傳感器可以實現大動態范圍5 Hz～100 Hz的角位移測量，測量誤差最大為0.220%，甚至在部分測試頻率時誤差為0.000%;累加誤差與角位移參數的測量誤差結果一致，且最大只有0.2°/s，說明傳感器動態特性良好，拓寬了其可測量的參數范圍，測量精度較高。

4 結論

本文針對常規彈藥彈體角位移參數的測量需求，提出了一種基于電磁感應原理的彈體旋轉角位移參數的測量方法，并設計了相應的傳感器。首先，利用電磁感應線圈采集彈體出膛后切割地磁場的信號;其次，采用自適應閉環頻率跟蹤測量算法，通過邊沿檢測和脈沖計數相結合的方式獲得彈體的實時角位移參數信息。通過半實物試驗和實物試驗分別對傳感器進行了性能測試，結果說明傳感器能夠對大動態范圍內的線圈輸出信號進行高精度的角位移測量，具有良好的實際適用性和可靠性，可以實現對彈藥彈體角位移參數的實時、高精度測量，具有一定的工程應用價值。

［1］ Filatov Y V，Pavlov P A，Venediktov V Y.Noncontact Measurement of Angular Position and Angular Movement by Means of Laser Goniometer［J］.Optical Engineering，2015，54(5):103－107.

［2］ Shan M G，Min R，Zhong Z，et al.Differential Reflective Fiber-Optic Angular Displacement Sensor［J］.Optics and Laser Technology，2015，68:124－128.

［3］ Gavrilin D A，Kuzin S V，Salashchenko N N，et al.Application of Point Diffraction Interferometry for Measuring Angular Displacement to a Sensitivity of 0.01 Arcsec［J］.Applied Optics，2015，54(31): 9315－9319.

［4］ Sakamoto J M，Pacheco G M，Kitano C，et al.Geometrical Parameter Analysis of a High-Sensitivity Fiber Optic Angular Displacement Sensor［J］.Applied Optics，2014，53(36):8436－8443.

［5］ Li K，Kuang C F，Liu X.Small Angular Displacement Measurement Based on an Autocollimator and a Common-Path Compensation Principle［J］.Review of Scientific Instruments，2013，84(1):108－114.

［6］ Wu C M，Chuang Y T.Roll Angular Displacement Measurement System with Microradian Accuracy［J］.Sensors and Actuators A: Physical，2004，116(1):145－149.

［7］ Payne D.Accurate Measurement of Angle Position at High Angular Velocities［J］.Sensors and Actuators A:Physical，2006，129 (1－2):239－242.

［8］ Tang Q F，Peng D L，Wu L，et al.An Inductive Angular Displacement Sensor Based on Planar Coil and Contrate Rotor［J］.IEEE Sensors Journal，2015，15(7):3947－3954.

［9］ Yang Y P，Ting Y Y.Improved Angular Displacement Estimation Based on Hall-Effect Sensors for Driving a Brushless Permanent-Magnet Motor［J］.IEEE Transactions on Industrial Electronics，2014，61(1):504－511.

［10］何森，王志斌.一種單目視覺標定飛機方向舵角位移的新方法［J］.兵工學報，2011，32(11):1384－1388.

［11］張宇鵬，徐鈺蕾，王昱棠.高精度電容式角位移傳感器測量方法［J］.儀器儀表學報，2014，35(6):147－150.

［12］王先全，雷毅談，張虹光，等.基于DSP的時柵位移傳感器誤差處理與系統設計［J］.傳感技術學報，2014，27(8):1054－1059.

［13］Naqui J，Martin F.Angular Displacement and Velocity Sensors Based on Electric-LC(ELC)Loaded Microstrip Lines［J］.IEEE Sensors Journal，2014，14(4):939－940.

［14］Harnsoongnoen S，Angkawisittpan N.Angular Displacement Sensor Based on Coplanar Waveguide(CPWs)Loaded with S-Shaped Golden Spiral-Tapered Split Ring Resonators(SGS-SRRs)［J］.Procedia Computer Science，2016，86:75－78.

［15］代金華，張麗杰.多準則MEMS陀螺隨機誤差在線建模與實時濾波［J］.傳感技術學報，2016，29(1):75－79.

［16］祿坡遠，劉詩斌，劉昭元，等.基于ADIS16354的姿態角傳感器設計［J］.傳感技術學報，2010，23(2):192－195.

［17］田蔚風，王俊璞，金志華.基于PSD的靜電陀螺儀角位移測量原理研究［J］.儀器儀表學報，2004，25(3):406－408.

武 丹(1991－)，女，現為中北大學在讀研究生，主要研究方向為智能信息處理，wudan910201@126.com;

李 劍(1985－)，男，現為中北大學講師，主要研究方向為新型傳感技術及多維信號處理，lijian851208@126.com;

韓 焱(1957－)，男，現為中北大學教授、博士生導師，主要研究方向為多維信號處理與重建、無損檢測技術，hanyan@ nuc.edu.cn。

A Measurement Method for Angular Displacement Parameter Based on the Electromagnetic Induction Principle

WU Dan*，LI Jian，HAN Yan
(Institute of Signal Capturing and Processing Technology，Key Laboratory of Shanxi Province，North University of China，Taiyuan 030051，China)

Aiming at the measurement requirements with an extremely high dynamic range and high precision for angular displacement parameter in the research field of conventional ammunition and projectile at present，this paper brings up a method for measuring angular displacement parameter based on the electromagnetic induction principle，and designs a corresponding angular displacement sensor as well.Induction coil is employed to acquire the information of projectile moving across geomagnetic field within a large dynamic range of rotational speed.Self-adaptive closed-loop frequency tracking measurement algorithm，which combines edge detection with pulse counting，is presented to measure the real-time information of angular displacement parameter in the process of the rotation of projectile.Accumulative error is eliminated by using the way of periodically pulse clear.The experimental results of semi-physical simulation and physical simulation demonstrate that the designed sensor not only can measure angular displacement within an extremely high dynamic range，broaden measurement range from 600°/s to 36 000°/s，but also can completely eliminate accumulative error during the measurement.The measurement error is less than 0.220%with the maximum accumulative error of lower than 0.2°/s.Thereby realizing real-time measurement with high precision for angular displacement parameter of ammunition and projectile.The proposed method has definite value to engineering application in the fields of attitude determination and geomagnetic navigation，etc.

angular displacement;self-adaptive closed-loop frequency tracking measurement;electromagnetic induction;FPGA

TP212.6

A

1004－1699(2017)02－0211－07

C:7230

10.3969/j.issn.1004－1699.2017.02.008

2016－07－30 修改日期:2016－09－27