爆炸沖擊條件下的加速度傳感器結(jié)構(gòu)分析*

劉 波，楊黎明，李東杰

(中國工程物理研究院電子工程研究所，四川綿陽621900)

爆炸沖擊條件下的加速度傳感器結(jié)構(gòu)分析*

劉 波，楊黎明*，李東杰

(中國工程物理研究院電子工程研究所，四川綿陽621900)

針對(duì)加速度傳感器在爆炸與沖擊測(cè)試中的應(yīng)用，從理論與有限元仿真出發(fā)，分析傳感器結(jié)構(gòu)的靜態(tài)響應(yīng)與沖擊響應(yīng)。在15.4×104gn的靜態(tài)載荷下，傳感器結(jié)構(gòu)最大應(yīng)力超過材料的許用應(yīng)力，將會(huì)發(fā)生結(jié)構(gòu)斷裂。在靜態(tài)載荷下，加速度傳感器在15.4×104gn的沖擊加速度載荷下結(jié)構(gòu)最大應(yīng)力超過材料的許用應(yīng)力，將會(huì)發(fā)生結(jié)構(gòu)斷裂。在加速度傳感器的工作方向上施加幅值為15×104gn，半周期為5 μs、10 μs、20 μs、30 μs、40 μs的半正弦加速度沖擊載荷。在幅值為15×104gn、半周期為30 μs的沖擊載荷下，傳感器的固定端處應(yīng)力為334 MPa，將會(huì)使傳感器斷裂失效。在幅值為15×104gn、半周期為5 μs、10 μs、20 μs的沖擊載荷下，固定端處應(yīng)力超過材料許用應(yīng)力，將也會(huì)發(fā)生結(jié)構(gòu)斷裂。懸臂梁在半周期為5 μs、10 μs、20 μs的沖擊下，將會(huì)出現(xiàn)斷裂。大體上，沖擊載荷的周期越小，固定端的應(yīng)力越大集中越嚴(yán)重。由于傳感器固有周期為9.5 μs，加速度傳感器在半周期為10 μs的沖擊載荷下出現(xiàn)諧振，固定端處應(yīng)力變大集中加劇。分析加速度傳感器在沖擊載荷下的結(jié)構(gòu)響應(yīng)為傳感器的結(jié)構(gòu)設(shè)計(jì)與具體應(yīng)用時(shí)的可靠性分析提供了理論依據(jù)。

沖擊振動(dòng);結(jié)構(gòu)響應(yīng);有限元分析;模態(tài)分析;加速度傳感器

彈體在侵徹靶標(biāo)時(shí)，彈體內(nèi)部的電子組件、裝藥等會(huì)受到彈體過載和彈體結(jié)構(gòu)振動(dòng)所引起的沖擊載荷。為了解分析電子組件、裝藥等的抗沖擊特性，就必須測(cè)試彈體侵徹靶標(biāo)過程中的沖擊載荷。在實(shí)際的爆炸與沖擊試驗(yàn)中，通常使用加速度傳感器、壓力傳感器等來測(cè)量試驗(yàn)過程中的沖擊力與過載加速度［1－2］。

這就要求加速度傳感器能夠承受爆炸與沖擊過程的高頻高沖擊載荷，中北大學(xué)［3］、北京理工大學(xué)［4］等研究了加速度傳感器在沖擊條件下的結(jié)構(gòu)響應(yīng)和失效類型。在實(shí)驗(yàn)室條件下，一般采用Hopkinson桿［5］或空氣炮［6］等對(duì)加速度傳感器進(jìn)行沖擊加載，Hopkinson桿所產(chǎn)生的加速度脈沖一般在幾十微秒到一兩百微秒，而實(shí)際的爆炸與沖擊載荷也有很高成分的高頻分量，而現(xiàn)目前很少有對(duì)加速度傳感器在高頻沖擊載荷下的沖擊響應(yīng)的研究。

目前國內(nèi)、外現(xiàn)有的侵徹加速度現(xiàn)場(chǎng)測(cè)試技術(shù)中［3］，較多采用彈載存儲(chǔ)測(cè)試技術(shù)，由加速度傳感器、記錄電路模塊和電池總共3部分組成的加速度現(xiàn)場(chǎng)測(cè)試模塊測(cè)試記錄試驗(yàn)過程中的加速度歷程。由于應(yīng)力波在傳感器安裝結(jié)構(gòu)中的傳播，加速度傳感器不僅會(huì)受到?jīng)_擊過載的影響，還會(huì)受到由于自身結(jié)構(gòu)振動(dòng)所引起的結(jié)構(gòu)響應(yīng)的影響［4］。加速度傳感器在沖擊載荷下的結(jié)構(gòu)響應(yīng)將直接影響傳感器的生存能力與測(cè)試的加速度歷程的準(zhǔn)確性［5］。

文中結(jié)合理論分析與有限元仿真［7］，分析加速度傳感器結(jié)構(gòu)的靜態(tài)力學(xué)響應(yīng)。接著利用不同半周期的半正弦沖擊載荷近似代表爆炸沖擊載荷［8－9］，分析加速度傳感器在爆炸與沖擊條件下的結(jié)構(gòu)響應(yīng)，比較了分析結(jié)果與靜力分析結(jié)果的差異和結(jié)構(gòu)應(yīng)力集中程度與沖擊加速度的半周期的關(guān)系，并由分析結(jié)果得到傳感器可能發(fā)生結(jié)構(gòu)失效的工況，為加速度傳感器的結(jié)構(gòu)設(shè)計(jì)與具體應(yīng)用時(shí)的可靠性分析提供理論依據(jù)。

1 加速度傳感器的結(jié)構(gòu)

加速度傳感器很多種結(jié)構(gòu)，比如懸臂梁－質(zhì)量塊［10］、三梁－質(zhì)量塊［11］、四梁－質(zhì)量塊［12］、五梁－雙質(zhì)量塊［13］、八梁－質(zhì)量塊［14］等等。懸臂梁－質(zhì)量塊結(jié)構(gòu)的加速度傳感器由于其固有頻率高、工藝簡(jiǎn)單等優(yōu)勢(shì)而被廣泛用于加速度現(xiàn)場(chǎng)測(cè)試中。在外界爆炸與沖擊載荷下，質(zhì)量塊發(fā)生位移導(dǎo)致懸臂梁發(fā)生變形，由分布在懸臂梁端部附近的壓敏電阻或者壓電晶體測(cè)得梁的變形，由懸臂梁變形與沖擊載荷的關(guān)系從而測(cè)得爆炸與沖擊載荷的強(qiáng)度。

2 加速度傳感器的靜態(tài)響應(yīng)

2.1 靜態(tài)理論分析

懸臂梁－質(zhì)量塊結(jié)構(gòu)的加速度傳感器的結(jié)構(gòu)關(guān)于zox平面對(duì)稱，可以簡(jiǎn)化為如圖1的平面圖。質(zhì)量塊整體受到工作方向上的沖擊加速度時(shí)，可以將其等效為作用于質(zhì)量塊質(zhì)心的集中力F，F(xiàn)=ρb2h22L2a。上式中，b2、h2和2L2為質(zhì)量塊的寬度、厚度和長(zhǎng)度，ρ為質(zhì)量塊材料的密度，a為沖擊加速度幅值。

圖1 結(jié)構(gòu)平面簡(jiǎn)圖

加速度傳感器的懸臂梁在作用于質(zhì)量塊質(zhì)心的集中力F下會(huì)發(fā)生變形，懸臂梁在外力作用下的彎曲方程為:

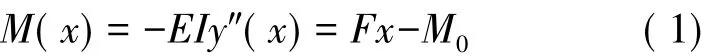
式中:I為懸臂梁的慣性矩，對(duì)于矩形截面梁，I= b1h31/12。根據(jù)力平衡及力矩平衡關(guān)系，得到懸臂梁固定端彎矩為M0=2ρb2h2L2a(L1+L2)。

代入加速度傳感器的懸臂梁結(jié)構(gòu)對(duì)應(yīng)的邊界條件y'(0)=0，y(0)=0，求解式(1)可以得到:

懸臂梁結(jié)構(gòu)x方向的應(yīng)力為:

懸臂梁x方向上最大的應(yīng)力發(fā)生在懸臂梁的固定端，為:

對(duì)加速度傳感器結(jié)構(gòu)進(jìn)行靜力分析，質(zhì)量塊－懸臂梁結(jié)構(gòu)的傳感器結(jié)構(gòu)尺寸參數(shù)如表1，材料采用線彈性模型，參數(shù)如表2。

表1 傳感器結(jié)構(gòu)尺寸 單位:μm

表2 傳感器材料參數(shù)

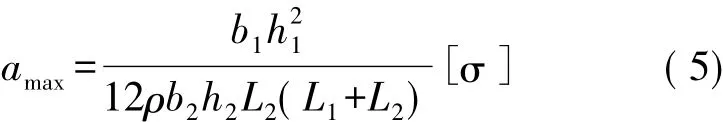
將加速度傳感器的尺寸與材料參數(shù)代入上式可以得知，當(dāng)外界爆炸或沖擊載荷超過15.4×104gn時(shí)，加速度傳感器懸臂梁上最大應(yīng)力會(huì)超過許用應(yīng)力，梁結(jié)構(gòu)將可能發(fā)生斷裂。

2.2 靜態(tài)仿真分析

利用ANSYS建立有限元模型，如圖2。有限元模型幾何尺寸參數(shù)與材料線彈性模型參數(shù)同表1、表2，有限元模型的單元采用3D solid 186單元，網(wǎng)格為六面體網(wǎng)格。

對(duì)加速度傳感器的質(zhì)量塊施加Z軸方向上的15×104gn加速度，加速度傳感器x方向的應(yīng)力分布如圖3所示。

加速度傳感器一般由單晶硅材料制成，工程上硅的許用應(yīng)力［σ］一般是330 MPa。當(dāng)梁上應(yīng)力超過330 MPa時(shí)，梁結(jié)構(gòu)將會(huì)發(fā)生斷裂。代入式(4)，得到加速度傳感器能承受的最大沖擊載荷:

圖2 傳感器有限元模型

圖3 傳感器結(jié)構(gòu)應(yīng)力分布

從圖3可以看出，在15×104gn的沖擊加速度下，懸臂梁固定端端部的應(yīng)力為402 MPa，質(zhì)量塊與懸臂梁連接處應(yīng)力為313 MPa。可以看出，懸臂梁固定端端部應(yīng)力超過了硅材料的許用應(yīng)力，梁結(jié)構(gòu)將可能發(fā)生斷裂。

將加速度a=15×104gn代入式(4)，得到加速度傳感器梁結(jié)構(gòu)上 x方向上最大應(yīng)力約為 330 MPa。與有限元分析結(jié)果存在20%左右的差距，在理論計(jì)算時(shí)，將傳感器固定端到質(zhì)量塊質(zhì)心的結(jié)構(gòu)簡(jiǎn)化為截面與懸臂梁一樣的結(jié)構(gòu)，部分梁截面變小，抗沖擊性能變低。

3 加速度傳感器的沖擊響應(yīng)仿真

傳感器結(jié)構(gòu)在沖擊載荷下的響應(yīng)將直接決定加速度傳感器的生存能力與加速度測(cè)試結(jié)果的準(zhǔn)確性。由于測(cè)試過程中彈體的振動(dòng)及傳感器安裝結(jié)構(gòu)本身的振動(dòng)，導(dǎo)致真實(shí)的沖擊載荷十分復(fù)雜。通常我們利用半正弦的沖擊脈沖去近似代表實(shí)際的沖擊載荷，半正弦的沖擊載荷通常由其沖擊幅值與沖擊半周期兩個(gè)量表征。加速度傳感器用于爆炸與沖擊載荷測(cè)試時(shí)，由于載荷峰值高(高達(dá)數(shù)萬gn，甚至數(shù)十萬gn)、持續(xù)時(shí)間短(短至幾百微妙，甚至幾微妙)。因此選擇半周期為5 μs、10 μs、20 μs、30 μs、40 μs的沖擊載荷加載在傳感器結(jié)構(gòu)上。

利用ANSYS中的非線性動(dòng)力有限元仿真模塊LS-DYNA對(duì)加速度傳感器結(jié)構(gòu)的沖擊響應(yīng)進(jìn)行了分析計(jì)算，有限元模型采用3D solid 164單元，網(wǎng)格為六面體網(wǎng)格。加速度傳感器結(jié)構(gòu)尺寸參數(shù)及材料線彈性模型參數(shù)如表1、表2。在加速度傳感器的工作方向上，施加峰值為15×104gn，半周期為5 μs、10 μs、20 μs、30 μs、40 μs的半正弦加速度沖擊載荷，如圖4所示。

圖4 不同周期的加速度載荷

分析得到加速度傳感器結(jié)構(gòu)在峰值為15×104gn，半周期為20 μs的加速度沖擊下的應(yīng)力分布云圖，如圖5所示。

從圖5可以看出，在峰值為15×104gn，半周期為20 μs的加速度沖擊載荷下，加速度傳感器的懸臂梁固定端與質(zhì)量塊端部出現(xiàn)應(yīng)力集中，懸臂梁固定端最大應(yīng)力為352 MPa，質(zhì)量塊與懸臂梁連接處最大應(yīng)力為211 MPa。在沖擊條件下，加速度傳感器的懸臂梁固定端比質(zhì)量塊與懸臂梁連接處更容易發(fā)生斷裂。選取懸臂梁固定端處26397號(hào)、26197號(hào)、25997號(hào)和25797號(hào)單元，如圖6所示。

圖5 傳感器應(yīng)力分布

圖6 選取的懸臂梁固定端節(jié)點(diǎn)

4個(gè)單元在相同峰值、不同半周期的加速度沖擊載荷下的應(yīng)力隨時(shí)間變化，如圖7所示。

從圖7可以看出，當(dāng)沖擊半周期為30 μs時(shí)，固定端最大應(yīng)力為334 MPa，正好就是材料的許用應(yīng)力。當(dāng)沖擊半周期小于30 μs時(shí)，固定端最大應(yīng)力均超過了材料的許用應(yīng)力，梁結(jié)構(gòu)在沖擊載荷下將會(huì)發(fā)生結(jié)構(gòu)斷裂。當(dāng)沖擊半周期為40 μs時(shí)，固定端最大應(yīng)力為317 MPa，未達(dá)到材料的許用應(yīng)力。

當(dāng)沖擊半周期為5 μs時(shí)，固定端最大應(yīng)力為441 MPa，當(dāng)沖擊半周期為10 μs時(shí)，固定端最大應(yīng)力為484 MPa;當(dāng)沖擊半周期為20 μs時(shí)，固定端最大應(yīng)力為352 MPa;當(dāng)沖擊半周期為40 μs時(shí)，固定端最大應(yīng)力為317 MPa。在半周期為5 μs、10 μs、20 μs的沖擊下，固定端最大應(yīng)力均超過了材料的許用應(yīng)力，在實(shí)際應(yīng)用時(shí)，梁結(jié)構(gòu)會(huì)出現(xiàn)斷裂。

圖7 不同半周期沖擊下固定端單元應(yīng)力曲線

提取25997號(hào)單元在不同半周期沖擊載荷下應(yīng)力隨時(shí)間的變化歷程，如圖8所示。從圖8可知，固定端最大應(yīng)力大體上隨加速度沖擊載荷的半周期變大而變小，說明半正弦沖擊載荷的周期越小，懸臂梁固定端就越容易發(fā)生斷裂。

圖8 不同半周期沖擊下25997號(hào)單元應(yīng)力曲線比較

但是半周期為10 μs的沖擊下懸臂梁上最大應(yīng)力卻大于半周期為5 μs的沖擊下固定端上最大應(yīng)力，推測(cè)可能是加速度傳感器的某一階固有周期在10 μs左右，傳感器結(jié)構(gòu)在半周期為10 μs的外界沖擊載荷下發(fā)生了諧振。

4 加速度傳感器結(jié)構(gòu)模態(tài)分析

利用ANSYS建立有限元模型，模型幾何參數(shù)與材料參數(shù)通表1、表2，有限元模型單元采用3D solid 186單元，網(wǎng)格為六面體網(wǎng)格。對(duì)結(jié)構(gòu)進(jìn)行模態(tài)分析，只提取了加速度傳感器結(jié)構(gòu)的一階固有頻率及固有振型，如圖9所示。

從圖9可以看出，該質(zhì)量塊－懸臂梁結(jié)構(gòu)的加速度傳感器的一階固有頻率為105.8 kHz，對(duì)應(yīng)其第1階固有周期9.5 μs。加速度傳感器在半周期為10 μs的加速度沖擊載荷下，結(jié)構(gòu)響應(yīng)發(fā)生諧振，懸臂梁端部應(yīng)力變大，進(jìn)而導(dǎo)致加速度傳感器結(jié)構(gòu)能承受的沖擊載荷的峰值降低。

圖9 傳感器一階振型

5 結(jié)論

針對(duì)加速度傳感器在爆炸與沖擊測(cè)試中的應(yīng)用，對(duì)一款懸臂梁—質(zhì)量塊結(jié)構(gòu)的加速度進(jìn)行了靜態(tài)分析與沖擊響應(yīng)仿真。在靜態(tài)條件下，加速度傳感器在15×104gn的沖擊條件下，梁結(jié)構(gòu)將會(huì)發(fā)生斷裂。對(duì)加速度傳感器施加峰值為15×104gn，半周期為為5 μs、10 μs、20 μs、30 μs、40 μs的半正弦加速度沖擊載荷。在半周期為30 μs時(shí)，固定端最大應(yīng)力正好達(dá)到材料許用應(yīng)力。大體上，半正弦沖擊載荷的周期越小，懸臂梁固定端的應(yīng)力越大。但是當(dāng)載荷周期接近結(jié)構(gòu)的固有頻率時(shí)，固定端的應(yīng)力會(huì)由于發(fā)生了諧振而變大。所以，當(dāng)加速度傳感器應(yīng)用于爆炸與沖擊測(cè)試時(shí)，應(yīng)了解傳感器與外界沖擊載荷的頻率特性，避免諧振現(xiàn)象的發(fā)生。

［1］ 陳學(xué)強(qiáng)，閆明明，徐曉輝，等.微加速度計(jì)在高沖擊下的斷裂失效分析［J］.儀表技術(shù)與傳感器，2014(2):16－19.

［2］ 蔡軍鋒，易建政，檀朝彬，等.PVDF壓電傳感器在爆炸沖擊博測(cè)量中的應(yīng)用［J］.傳感器世界，2005，11(3):13－15.

［3］ 張賀，石云波，唐軍.高量程加速度傳感器在測(cè)試中的失效分析［J］.傳感技術(shù)學(xué)報(bào)，2011，24(10):1422－1425.

［4］ 黃正平，龍仁榮.在爆炸與沖擊條件下構(gòu)件的加速度測(cè)量與加速度傳感器的標(biāo)定［C］//第十屆全國沖擊動(dòng)力學(xué)學(xué)術(shù)會(huì)議，2011.

［5］ 楊志才，石云波，董勝飛.基于雙彈頭Hopkinson桿的高g值加速度傳感器的動(dòng)態(tài)線性分析［J］.傳感技術(shù)學(xué)報(bào)，2015(7): 972－976.

［6］ 夏偉強(qiáng)，馬鐵華，范錦彪.壓電式加速度傳感器在高沖擊環(huán)境下的零漂分析［J］.傳感技術(shù)學(xué)報(bào)，2007，20(7):1522－1527.

［7］ 彭述成，溫志渝，溫中泉，等.真空微電子加速度傳感器結(jié)構(gòu)的有限元分析［J］.微納電子技術(shù)，2013，40(7):292－294.

［8］ Srikar V T，Senturia S D.The Reliability of MicroelectromechanicalSystems(MEMS)in Shock Environment［J］.Journal of Microelectromechanical Systems，2002，11(3):206－214.

［9］ Tanner D M，Walraven J A，Helgesen K.MEMS Reliability in Shock Environments［J］.IEEE International Reliability Physics Symposium，2000:129－138.

［10］陳宏，鮑敏杭，胡澄宇.硅壓阻式加速度傳感器的結(jié)構(gòu)研究［J］.復(fù)旦學(xué)報(bào)，1996(5):538－544.

［11］董培濤，周偉，李昕欣，等.三梁－質(zhì)量塊敏感結(jié)構(gòu)高性能壓阻式碰撞加速度計(jì)［J］.傳感技術(shù)學(xué)報(bào)，2007，24(8):1118－1121.

［12］趙銳，石云波，唐軍，等.MEMS面內(nèi)大量程加速度傳感器設(shè)計(jì)與分析［J］.傳感技術(shù)學(xué)報(bào)，2011，24(8)1118－1121.

［13］楊文碩.雙島－五梁式微型加速度傳感器的結(jié)構(gòu)分析［J］.計(jì)量學(xué)報(bào)，2002，23(3):199－204.

［14］張永平，何常德，張娟婷，等.一種壓阻式八固支梁三軸加速度傳感器［C］//全國半導(dǎo)體器件技術(shù)、產(chǎn)業(yè)發(fā)展研討會(huì)暨中國微納電子技術(shù)交流與學(xué)術(shù)研討會(huì)，2013.

劉 波(1990－)，男，漢族，碩士研究生，主要從事高量程加速度傳感器結(jié)構(gòu)分析、動(dòng)態(tài)測(cè)試等方面的研究，695423813@ qq.com;

楊黎明(1971－)，中國工程物理研究院電子工程研究所高級(jí)工程師，研究方向?yàn)閭鞲衅髟O(shè)計(jì)，felstone@vip.sina.com。

Structural Analysis of Micro-Accelerometer Under Blast and Impact Load*

LIU Bo，YANG Liming*，LI Dongjie
(Institute of Electronics Engineering of China Academy of Engineering Physics，Mianyang Sichuan 621900，China)

For the application of micro-accelerometer in the measurement of blast and impact load，the sensor’s static and impact structural response are analyzed by theoretical method and finite element analysis.Under static load，the max stress on the beam would exceed the allowable stress which will lead to the rupture of the accelerometer.In the working direction of accelerometer，the half-sine shock pulses with the same peak(15×104gn)and different semiperiod(5 μs，10 μs，20 μs，40 μs)are added to the mass of the sensor.The cantilever will break under the shock whose semi-period is 5 μs，10 μs and 20 μsbecause of the stress centralization.The max stress on the sensor exceeds the allowable stress under a static load of 15×104gn，which will lead to the rupture of the accelerometer.Under a shock load whose peak is 15×104gnand semi period is 30 μs，the stress of the sensor’s fixed end is 334 MPa that may cause the fracture of the sensor.The sensor will also break under the shock load with the peak is 15×104gnand the semiperiod is 5 μs，10 μs，20 μsfor the fixed end’s stress exceeds the allowable stress.The smaller the period is，the bigger of stress is.The resonance arises when the structure is loaded by the impact with a cycle of 10 μs for the inherent cycle is 9.5 μs，which leads to a increase of the stress.The analysis of structure response of accelerometerunder shock pulse offers theoretical according for the structural design and the construe of reliability of the accelerometer.

impact and vibration;structural response;finite element analysis;modal analysis;accelerometer

C:7230

10.3969/j.issn.1004－1699.2017.02.005

O327

A

1004－1699(2017)02－0194－06

項(xiàng)目來源:中國工程物理研究院電子工程研究所科技創(chuàng)新基金項(xiàng)目(S20161102)

2016－07－07 修改日期:2016－08－31