基于ZIP模型的零膨脹檢驗方法的比較研究

王平鮮+黃介武+常國艷

摘要針對已存在關于零膨脹的R檢驗、C檢驗、Score檢驗、卡方檢驗、似然比檢驗、Wald檢驗和基于置信區間檢驗，通過Monte Carlo模擬分析方法，在功效和犯第一類錯誤比例的意義下，在不同零膨脹程度、不同均值和不同樣本量下對上述檢驗作比較研究.得到了不同條件下7種檢驗方法的優良性，并結合理論對7種檢驗方法進行分析.

關鍵詞零膨脹；模擬；檢驗功效；第一類錯誤

中圖分類號O212.1文獻標識碼A

1引言

計數數據是一種廣泛存在于醫學、保險和農林等領域的數據類型.當計數數據中零的比例超出泊松（Poisson）或負二項（NB）分布等一般計數模型的預測能力，這類現象被稱為計數資料的零膨脹[1].針對存在零膨脹現象的計數數據，常見的統計分析模型有零膨脹泊松模型、零膨脹負二項回歸模型等.而在用零膨脹模型對數據進行擬合分析時，首先要對數據是否存在零膨脹進行檢驗.關于數據是否存在零膨脹，一方面可以通過直方圖等做簡單的直觀分析與判斷，但所得結論較為粗糙[2]；另一方面可以通過建立檢驗統計量進行假設檢驗，得到較為精確的結論.1954年Cohran[3]提出了一個不考慮協變量的C檢驗，1956年Rao和Chakravarti[4]針對小樣本量提出另一個考慮協變量的R檢驗，這兩種檢驗方法只考慮響應變量的觀測值，相對較為直接.1985年ElShaarawi[5]推導了基于ZIP模型下似然比檢驗的統計量，并通過模擬分析比較了R檢驗、C檢驗和似然比檢驗的功效.1995年Van den broek[6]提出了基于零膨脹泊松（ZIP）模型下的Score檢驗；2001年M.Xie[7]提出了基于ZIP模型的基于置信區間檢驗，并通過模擬方法對C檢驗、R檢驗、似然比檢驗、Score檢驗、基于置信區間的檢驗和卡方檢驗的功效進行比較；2009年Saranya Numna[8]提出了基于ZIP模型下的Wald檢驗.

本文在基于ZIP模型條件，通過Monte Carlo模擬分析方法，在功效和犯第一類錯誤比例的意義下，對上述的R檢驗、C檢驗、Score檢驗、卡方檢驗、似然比檢驗、Wald檢驗和基于置信區間檢驗在不同零膨脹程度、不同均值和不同樣本量下作比較研究.

2零膨脹模型及零膨脹檢驗方法介紹

2.1零膨脹泊松（ZIP）模型

零膨脹（ZI）模型的基本思想是認為事件的發生數來自于兩部分：一部分隨機變量的取值只為零（這部分零稱為結構零），另一部分來自一個離散分布（此時的零稱為抽樣零），由此可得零膨脹模型的一般形式是：

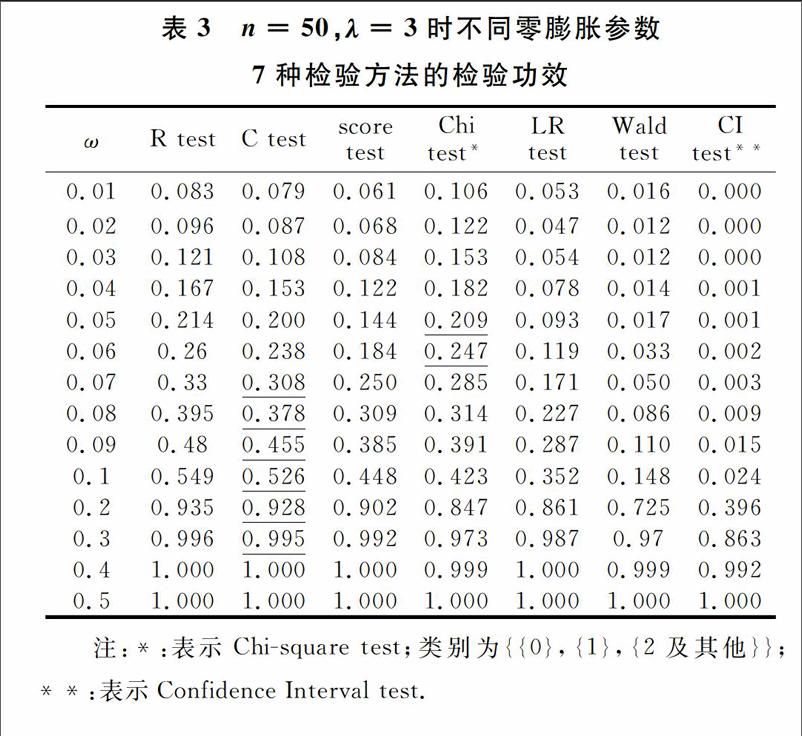
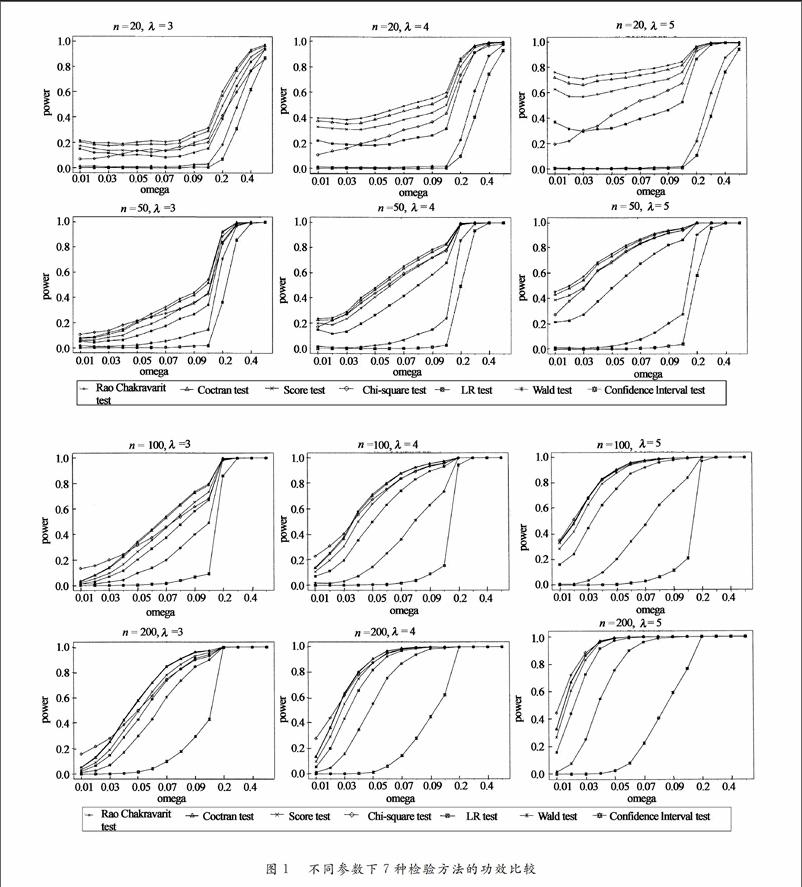
再對圖1的模擬結果進行分析.首先考慮λ變化、n不變條件下觀察不同零膨脹的功效.從圖1模擬結果看出，隨著λ的增大，Wald檢驗和基于置信區間的檢驗與其他5種檢驗的功效差距逐漸增大.

然后考慮n變化、λ不變條件下觀察不同零膨脹的功效.從圖1可以看出，當n比較小（如n=20，50）時，R檢驗和C檢驗的功效高于其他檢驗的功效.當n比較大，ω比較小（如n=100，200，ω<0.05）時，卡方檢驗的功效最高；而當n和ω比較大（如n=100，200，ω>0.05）時，7種檢驗方法的功效差別不明顯.

綜合模擬結果可知，大多數情況，R檢驗法和C檢驗法對零膨脹檢驗的功效高于其他5種檢驗，其它檢驗的功效大小依次為：Score檢驗>卡方檢驗>似然比檢驗>Wald檢驗>基于置信區間檢驗.

3.2模擬檢驗方法犯第一類錯誤的比例

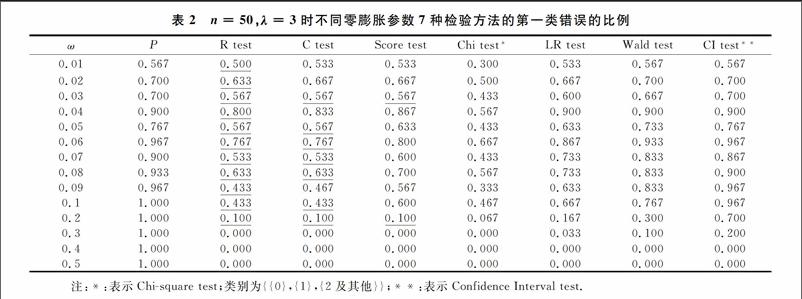
通過犯第一類錯誤的比例對7種檢驗方法進行比較分析.這里只考慮n=50，λ=3的情況，ω的取值和隨機數產生的方法同上.對每組參數，實驗均重復3 000次.實驗結果見表2，其中P表示同一組參數對應的3 000組數據中存在零膨脹的比例.模擬結果見表2.

表2中的傾斜加粗表示犯第一類錯誤的最小值，傾斜加下劃線表示第二小的值.從表2模擬結果可以看出，當n=50，λ=3時，在不同零膨脹程度下，卡方檢驗犯第一類錯誤的比例總是最小，而R和C檢驗犯第一類錯誤的比例大于卡方檢驗小于其他四種檢驗.此外，從表2模擬結果同樣可知，在給定的n=50，λ=3的條件下，隨著零膨脹程度的增加，7種檢驗方法犯第一類錯誤的比例均有減少的趨勢.

4結論

本文在以檢驗功效和犯第一類錯誤比例為評判準則下，通過Monte Carlo模擬分析方法，對已存在的R檢驗、C檢驗、Score檢驗、卡方檢驗、似然比檢驗、Wald檢驗和基于置信區間檢驗作了比較研究.得出7種零膨脹檢驗方法可以有效的檢驗零膨脹是否存在；其中，基于置信檢驗的功效最低，主要原因在于該方法對零假設有非常強的保護；雖然R檢驗和C檢驗的功效比其他5種檢驗的功效大，即“納偽”的概率比其他五種檢驗小，但是這兩種檢驗方法因不考慮協變量，有時候會導致信息的丟失.卡方檢驗犯第一類錯誤的比例比其他檢驗的低，即“棄真”的概率低，但是，卡方檢驗是基于均值與方差相等的Poisson模型，所以卡方檢驗有時會導致納入過多的錯誤信息，如可能考慮了過度離散情況.似然比檢驗、Score檢驗和Wald檢驗是基于ZIP模型，所以更能反映真實情況，而Score檢驗的統計量是最簡潔的.在應用過程中，零膨脹作為一種現象只是相對而言，因此針對具體問題，應該仔細觀察和考慮可能同時存在的其他特殊情況，以選擇合適的模型進行擬合.

參考文獻

[1]王存同. 零膨脹模型在社會科學實證研究中的應用——以中國人工流產影響因素的分析為例[J]. 社會學研究， 2010（5）：130-148.

[2]謝鋒昌.零過多數據的統計分析及其應用[M].北京：科學出版社， 2013.

[3]Cochran W G.Some metools for stengthening the canman X2 test[J].Biometrics，1954，10（4）：417-451.

[4]Rao C R，Chakravarti I M. Some small sample tests of significance for a poisson distribution[J]. Biometrics， 1956， 12（3）： 264-282.

[5]ElShaarawi A H. Some goodnessoffit methods for the poisson plus added zeros distribution[J]. Applied and Environmental Microbiology， 1985， 49（5）：1304-1306.

[6]Van d B J. A score test for zero inflation in a poisson destruction[J]. Biometrics， 1995， 51（2）：738-743.

[7]Xie M，He B，Goh T N. Zeroinflated Poisson model in statically process control[J]. Computational Statistics & Data Analysis， 2001， 38（2）：191-201.

[8]Numna S，Jansakul N. Analysis of extra zero counts using zeroinflated Poisson models [D].Prince：Prince Mathematics and Statistics Prince of Songkla University， 2009.

[9]王星. 非參數統計[M]. 北京：清華大學出版社， 2009.