對重尾分布及現象的探討

葉南吉

摘 要 在現實生活中，重尾現象隨處可見。本文針對重尾的概念、現象及一些風險測量方法如VaR、EVT進行了介紹，希望可以引起人們對極端損失的關注和更深入的研究。

關鍵詞 尾部分布；重尾現象；風險價值度VaR

一、重尾的概念及現象

1.何為重尾

重尾也稱長尾、肥尾。概率統計中，重尾分布是一種機率分布的模型，其特點是尾部比指數分布還要厚。在金融領域，我們通常以投資證券的收益作為橫坐標研究收益的概率分布，因而右邊尾部（損失）的分布會比較受到重視，但左邊尾部比較厚，或是兩邊尾部都很厚的狀況，也會被認為是一種重尾分布。

2.重尾現象

自然界中的重尾現象表現在少量個體占用大量資源，比如空氣中氮氣與氧氣的比例約為78：21；人腦中水與其他物質之比例大概是80：20……。

在金融市場上，重尾帶來的災難性后果也無處不在。它暗喻著客觀世界的極端波動性，指那些發生概率雖低，但一旦發生就會產生毀滅性沖擊的事件，像颶風、火災、重大車禍等。放眼歷史，2011年3月11日發生在日本的里氏9級大地震導致日經指數在一周內下跌12.85%；同年7月23日，甬溫線動車追尾事件導致了次日滬市暴跌82.04點；最令人難忘的應該是08年美國次貸危機，其輻射范圍之廣，影響之惡劣令人唏噓。凡次種種，都在告誡各個部門企業乃至國家加強對未知事物的風險管理。

二、重尾分布在概率論中的解釋

在概率論中，取正值的連續隨機變量的k階原點矩定義為 ，這個積分結果依賴于密度函數f（x）和k，當然也可能積分不存在，如果在x很大時密度函數也很大，就有可能會導致積分不收斂。對于一個隨機變量，如果任意的正數階原點矩存在，那么說明分布的尾部很輕，而正數階矩存在最高階數（或不存在正數階矩），則說明分布的尾部很厚。

19世紀末期，意大利經濟學家維弗雷多·帕累托認為，貧與富的存在，既是經濟問題，也有政治原因。帕累托在研究英國人的收入分配問題時發現，絕大部分社會財富最終總會流向少數人群；他還發現，某一部分人口占總人口的比例，與這一部分人所擁有的財富的份額具有比較確定的計量經濟關系。進一步的研究證實，這種不平衡模式可以重復出現，甚至可以預測。經濟學把這一社會財富的分布狀態，稱為“帕累托分布”。Pareto型隨機變量屬于常見的重尾分布族，包括Pareto分布、Burr分布和Frechet分布等，定義如下：

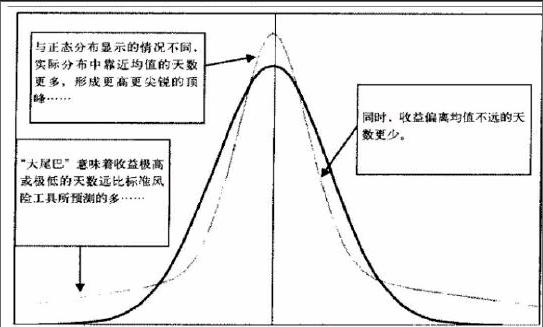
尖峰厚尾是我們經常遇到的一種分布狀態，偏度和峰度都是描述分布形狀的特征數。偏度對應隨機變量的三階矩，是描述分布偏離對稱性程度的一個特征數；而峰度則對應著四階矩，是相對于正態分布而言的超出量。對于一個標準正態分布而言，它的偏度skew=0，峰度kurtosis=3，因此當我們說一個分布有厚尾時也就表明它的峰度值大于3。如下圖很好地對比了正態分布與一個尖峰厚尾分布。

三、衡量尾部風險常用方法

1.VaR的優缺點分析

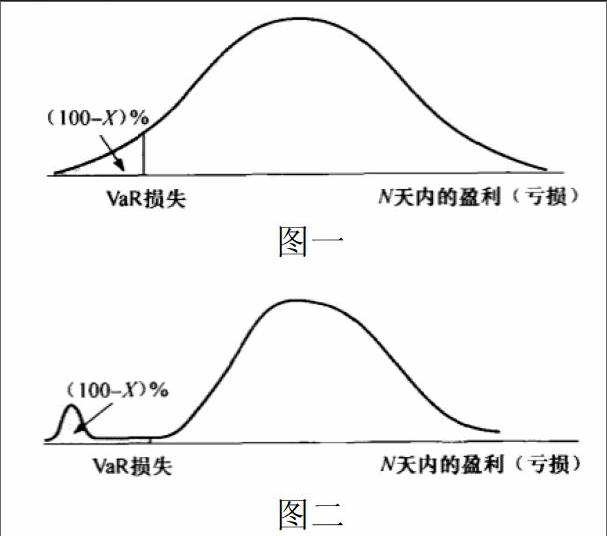
在金融領域中，金融機構常常用在險價值（value at risk ， VaR）來度量市場中的風險程度，VaR（V）是兩個參數（時間展望期N和置信度X%）的函數，可以表達成：我有X%的把握，在今后的N天內損失不會超過V。這看似是一個非常有效的風險測量方式，但它并不是一個一致的風險測量方式，因為它并不能滿足風險的次可加性，即兩個投資組合的VaR之和大于將兩者合并之后組成的新的投資組合的VaR。而次可加性是任何一個風險度量必須滿足的重要性質，它刻畫了現代投資組合理論中的風險分散化原則，是資產組合決策問題的一個基本條件。如下圖中兩者都表示投資組合價值變化概率分布，且圖二為圖一的變形，我們可以觀察到，盡管VaR值相同，但圖二的潛在損失明顯大于圖一，直接使用VaR判斷很可能使得交易員選擇圖二中分布特性的投資組合，帶來更高的風險。

2.VaR基礎上的改進

基于傳統方法在估計VaR時存在的缺陷，近年發展起來了極值理論（EVT），該理論只對資產收益的尾部數據進行分析而不考慮整體回報率，從而能更加直接地描述小概率的極端數據并進行模擬，考慮到了現實中可能發生的極端風險又可以規避一定的模型誤差，對傳統VaR的不足作出了一定的完善。

四、結論與展望

證券資產投資收益、保險索賠及許多人類行為都表現出重尾特征，如何準確估計重尾指數一直是我們研究的重點。人們總是對資產收益率的大起大落的情況更為關注，如股票的暴漲和暴跌就表現在股票極端收益率上，而這些都是由收益率分布的尾部特征所決定。又如對保險公司來說，對可能發生的極端事件而導致的巨額索賠需要進行大量數據的分析整理，去準確合理地定出保費，便于有效管理風險。因此，每一個風險管理者都需要做好對尾部風險的防范及對沖，在充滿不確定性的未知世界中把握住自己前進的方向。

參考文獻：

[1]陳思思.關于保險與金融中重尾現象的若干研究，浙江工商大學，2012

[2]邢紅衛.重尾現象、重尾分布與重尾指數估計，山西大學，2010

[3]John C.Hull，Options，Futures And Other Derivatives（Eighth

Edition），2012