一類非線性偏微分方程的多孤子解
李 偉,張智欣
(渤海大學(xué) 數(shù)理學(xué)院,遼寧 錦州 121013)
一類非線性偏微分方程的多孤子解
李 偉,張智欣
(渤海大學(xué) 數(shù)理學(xué)院,遼寧 錦州 121013)
許多重要的自然科學(xué)問題和工程問題都可以歸結(jié)為非線性偏微分方程。從傳統(tǒng)的角度來看,非線性偏微分方程的多孤子解是很難得到的。經(jīng)過幾十年的研究和探索,已經(jīng)發(fā)現(xiàn)了一些構(gòu)造精確解的方法。借助于科爾-霍普夫變換和Af+B=0方法,獲得了Burgers方程和KP方程的多孤子解。該方法能夠解決一系列偏微分方程。
科爾-霍普夫變換;Af+B=0方法;多孤子解
1 Introduction
Soliton is an important feature of nonlinearity and can be found in many scientific applications.Many systematic methods are used for studying the nonlinear evolution equations that give rise to solitons.The inverse scattering method, the Backlund transformation method, the Darboux transformation method, the Hirota bilinear method[1-5], and the Hereman-Nuseir method[6] are the most commonly used methods.The Hirota’s bilinear method is rather heuristic and possesses significant features that make it practical for the determination of multiple soliton solutions[7-13].developed a modified form of the Hirota’s method that facilitates the computational work.The computer symbolic systems such as Maple, Mathematica can be used to overcome the tedious calculations.
In this work, we will examine two kinds of equations that play a significant role in this field.The Burgers equation, theKPequation that will be examined, reads
(1)
(2)
In this work we will employ the Cole-Hopf transformation method and theAf+B=0 method to handle these two equations.We aim to obtain multiple-kink solutions for each equation.
2 The Af+B=0 method
We will consider the NPED
(3)
Our specific practice:
We first use the Cole-Hopf transformation
(4)
that will carry (3) to
Af+B=0
(5)
whereA,Bare the functions offx,ft,fxx,ftt,fxt, …, do not containf.
We set up
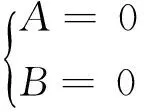
(6)
then the solution of (6) is solution of(5).
1) for single solution, we use
(7)
Substituting (7) into (6) and solvingr1, we findr1=r1(p1).
2) for two-solition solutions, we use
(8)
Substituting (8) into (5) and solvinga12, we finda12=a12(p1,p2).
3) for three-solition solutions, we use
(9)
Substituting (9) into (5) and solvingb123, we findb123=b123(p1,p2,p3).
3 The Burgers equation
We first use the Cole-Hopf transformation
that will carry (1) to
(11)
We set up
(12)
For single solution, we use
(13)
Substituting (13) into (12) and solving r1, we find
(14)
wherep1is arbitrary constant.
Substituting (13) and (14) into (10) give the single-kink solution
(15)
Therefore, we assume that the two-kink solutions for
(16)
wherep1,p2are arbitrary constants.
Substituting (16) into (11) and solvinga12, we find
(17)
Substituting (16) and (17) into (10) give the two-kink solutions
(18)
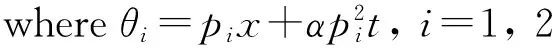
For three-solition solutions, we set
(19)
Substituting (19) into (11) and solvingb123, we find
(20)
Substituting (19) and (20) into (10) give the three-kink solutions
(21)
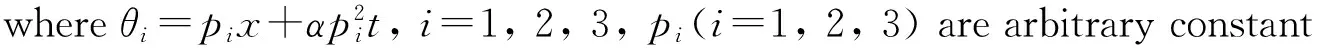
4 The KP equation
We use the Cole-Hopf transformation
(22)
that will carry the KP equation(2) to
(23)
We set up
(24)
For single solution, we use
(25)
Substituting (25) into (24) and solvingr1, we find
(26)
wherep1,q1are arbitrary constants.
Substituting (25) and (26) into (22) give the single-kink solution
(27)
Therefore, we assume that the two-kink solutions for
(28)
wherep1,p2are arbitrary constants.
Substituting (28) into (23) and solvinga12, we find
(29)
Substituting (28) and (29) into (22) give the two-kink solutions
(30)
wherep1,p2are arbitrary constants.
For three-solition solutions, we set
(31)
Substituting (31) into (23) and solvingb123, we find
(32)
Substituting (31) and (32) into (22) give the three-kink solutions
(33)
wherepi(i=1, 2, 3) are arbitrary constants.
5 Discussions
Two models, the Burgers equation, and theKPequation are studied.Multiple-kink solutions are formally derived for each equation.The results obstained we generalized to some equation.
[1] ABLOWITZ M J,KAUP D J,NEWELL A C,et al.The Inverse scattering transform Fourier analysis for nonlinear problems Stud[J].Appl Math,1974,53:249-315.
[2] ESTEVEZ P G,CONDE E,GORDOA P R.Unified approach to Miura,Backlund and Draboux transformations for nonlinear partial differential equations[J].Nonlinear Math.Phys.1998,5(1):82-114.
[3] HIROTA R.The Direct Method in Soliton Theory[M].Cambridge:Cambridge University Press,2004.
[4] HIROTA R.Exact solutions of the Korteweg de Vries equation for multiple collisions of solitons[J].Phys Rev Lett,1971,27(18):1192-1194.
[5] HIROTA R,SATSUMA J.N-soliton solutions of model equations for shallow water waves[J].Phys Soc Jpn,1976,40(2):611-612.
[6] HEREMAN W,NUSEIR A.Symbolic methods to construct exact solutions of nonlinear partial differential equations[J].Math Comput Simul,1997,43:105-109.
[7] MATSUNO Y.Bilinear Transformation Method[M].[s.n.]:Academic Press,1984.
[8] WAZWAZ A M.Integrable (2+1)-dimensional and (3+1)-dimensional breaking soliton equations[J].Phys Scripta,2010,81:035005.
[9] WAZWAZ A M.Multiple soliton solutions for coupled KdV and coupled KP Systems[J].Can J Phys,2010,87(12):1227-1232.
[10]WAZWAZ A M.Multiple soliton solutions for the (2+1)-dimensional asymmetric Nizhanik-Novikov-Veselov equation Nonlinear Anal[J].Theory Meth Appl,2010,72:1314-1318.
[11]WAZWAZ A M.The (2+1) and (3+1)-dimensional CBS equation:multiple soliton solutions and multiple singular soliton solutions.Multiple Zeitschrift fur Naturforschung A (ZNA),2010,65a:173-181.
[12]WAZWAZ A M.The Hirota’s direct method for multiple-soliton solutions for three model equations of shallow water waves[J].Appl Math Comput,2008,201:489-503.
[13]WAZWAZ A M.Solitary wave solutions of the the generalized shallow water wave (GSWW) equation by Hirota’s method,tanh-coth method and expfunction method[J].Appl Math Comput,2008,202:275-286.
(責(zé)任編輯 陳 艷)
N-Soliton Solutions for a Class of Nonlinear Partial Differential Equations
LI Wei,ZHANG Zhi-xin
(College of Mathematical, Bohai University, Jinzhou 121013, China)
Many significant natural science and engineering problems can be attributed to nonlinear partial differential equation. From the traditional point of view, n-soliton solutions of partial differential equation are hard to get. After several decades of research and exploration, we have found some tectonic exact solution method. With the help of Cole-Hopf transformation method and theAf+B=0 method, n-soliton solutions of the Burgers equation and the KP equation were presented. This method could solve a series of partial differential equations.
the Cole-Hopf transformation;Af+B=0 method; multiple-soliton solution
2016-11-24 基金項(xiàng)目:國(guó)家自然科學(xué)基金資助項(xiàng)目(11547005)
李偉(1977—),男, 遼寧錦州人,碩士,主要從事偏微分方程研究, E-mail:1344462965@qq.com。
李偉,張智欣.一類非線性偏微分方程的多孤子解[J].重慶理工大學(xué)學(xué)報(bào)(自然科學(xué)),2017(3):171-174.
format:LI Wei,ZHANG Zhi-xin.N-Soliton Solutions for a Class of Nonlinear Partial Differential Equations[J].Journal of Chongqing University of Technology(Natural Science),2017(3):171-174.
10.3969/j.issn.1674-8425(z).2017.03.026
O175.2
A
1674-8425(2017)03-0171-04

