矩陣方程ATXA=C的對(duì)稱M對(duì)稱最佳逼近解
徐玉霞,雷英杰,侯 強(qiáng)
(中北大學(xué) 理學(xué)院,太原 030051)
矩陣方程ATXA=C的對(duì)稱M對(duì)稱最佳逼近解
徐玉霞,雷英杰,侯 強(qiáng)
(中北大學(xué) 理學(xué)院,太原 030051)
在結(jié)構(gòu)動(dòng)態(tài)模型修正中,通常需要修正剛度矩陣與質(zhì)量矩陣以滿足正交條件。通過(guò)研究它們的極小二乘逼近解對(duì)其進(jìn)行修正。故在對(duì)稱M對(duì)稱矩陣集中,利用標(biāo)準(zhǔn)相關(guān)分解(CCD),獲得了矩陣方程ATXA=C的對(duì)稱M對(duì)稱極小二乘解;在此基礎(chǔ)上應(yīng)用廣義奇異值分解(GSVD)和投影定理,得到了給定矩陣的極小二乘解的對(duì)稱M對(duì)稱最佳逼近解。
對(duì)稱M對(duì)稱矩陣;投影定理;標(biāo)準(zhǔn)相關(guān)分解;極小二乘解;最佳逼近解
1 預(yù)備知識(shí)
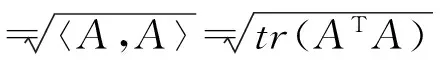
定義[1]設(shè)M∈Rn×m,若矩陣X∈SRn×n,滿足(MTXM)T=MTXM,則稱矩陣X為對(duì)稱M對(duì)稱矩陣。
矩陣方程ATXA=C來(lái)源于振動(dòng)理論逆問(wèn)題,這一問(wèn)題在機(jī)械系統(tǒng)和土木工程結(jié)構(gòu)中有實(shí)際應(yīng)用背景[2-3]。比如在修復(fù)振動(dòng)模型中往往需要滿足以下正交條件:
ATMA=Im,ATKA=Δ
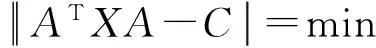

2 問(wèn)題1的解

(1)
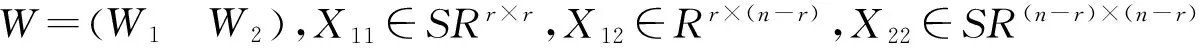

(2)
其中:Q∈ORm×m是正交陣;M∈Rr×r,N∈R(n-r)×(n-r)是非奇異矩陣。
且
進(jìn)一步,記
(3)
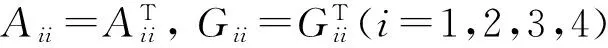
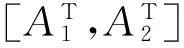
這里:
(4)
其中F11、G11和Ai4、Fi1、F1i、F4i、Fi4、G4i、Gi4(i=1,2,3,4)是任意矩陣。
(5)
將式(2)~(3)代入式(5)并利用Q的正交性可得
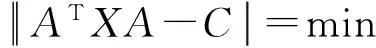
對(duì)式(6)求極小二乘解可得:
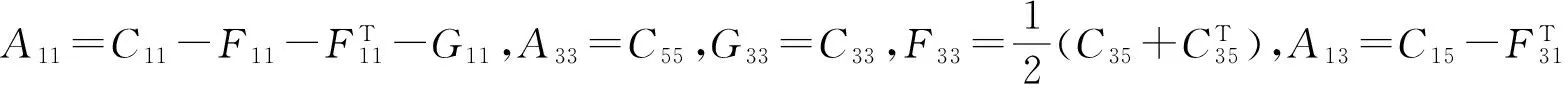
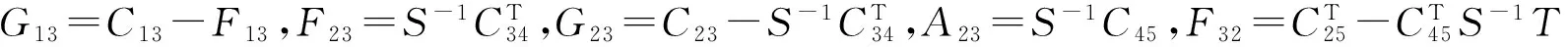
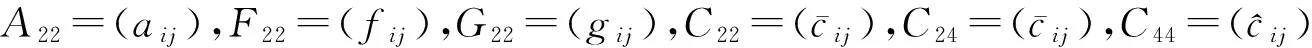
(8)
而f(aij,fij,gij)是關(guān)于aij、fij、gij的凸連續(xù)可微函數(shù)。故式(8)成立,當(dāng)且僅當(dāng)
直接計(jì)算可得
將其寫(xiě)成矩陣形式為
從而
最后,將所有極小二乘解代入式(3)則得式(4),其中F11、G11和Ai4、Fi1、F1i、F4i、Fi4、G4i、Gi4(i=1,2,3,4)是任意矩陣。證畢。
3 問(wèn)題2的解
由于式(2)中非奇異矩陣M、N不滿足Frobenius范數(shù)的正交不變性,故直接通過(guò)問(wèn)題1的解無(wú)法解決問(wèn)題2。為了解決問(wèn)題2,給出以下投影定理:

下面利用定理2將問(wèn)題2的極小二乘問(wèn)題轉(zhuǎn)化為求一相容矩陣方程的解的問(wèn)題。
引理2 給定矩陣A1和A2,如式(2),令C∈SRm×m,定義矩陣方程
(9)
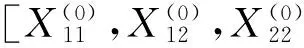
(10)
那么矩陣方程
(11)
是相容的,且它的解集與矩陣方程(9)的極小二乘解的解集一樣。
證明 根據(jù)文獻(xiàn)[3]的定理4.3可知引理2顯然成立。證明完畢。
基于以上引理,將式(2)、(4)代入式(10),可求得唯一矩陣C0。
接下來(lái),利用GSVD求方程(11)的相容解,此相容解也即非相容矩陣方程(9)的極小二乘解。
矩陣對(duì)[A1,A2]的GSVD為A1=UΠ1M,A2=VΠ2M,U∈ORr×r,V∈OR(n-r)×(n-r),M∈Rm×m是一非奇異矩陣,且
(12)
其中:Λ=diag(ξ1,…,ξk1+k2-m),1>ξ1≥…≥ξk1+k2-m>0;Γ=diag(η1,…,ηk1+k2-m),0<η1≤…≤ηk1+k2-m<1,Λ2+Γ2=Ik1+k2-m。
記矩陣UTX11U,UTX12V,VTX22V,M-TC0M-1有如下劃分形式:
(13)
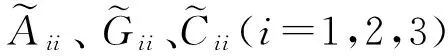
定理3 已知列滿秩矩陣A∈Rn×m,C∈SRm×m,矩陣UTX11U,UTX12V,VTX22V,M-TC0M-1有式(13)的劃分形式,則矩陣方程(11)的相容解(也即非相容方程(9)的極小二乘解)為:
(14)
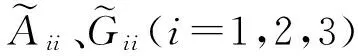
證明 將式(1)、(4)以及A1、A2代入式(11)并根據(jù)W的非奇異性可得
(15)
接下來(lái),將式(12)、(13)代入(15)直接計(jì)算可得式(14)。證畢。
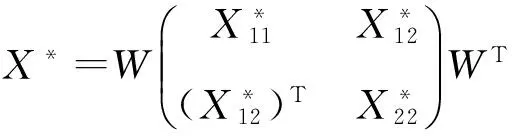
(16)
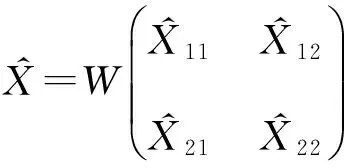
(17)
其中:
(18)
(19)
(20)
(21)
(22)
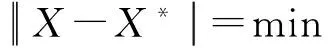
(23)
(24)
(25)
對(duì)于式(23)~(25),采用類似式(7)的處理方法直接計(jì)算可得式(19)~(22)。最后將所求得的所有極小二乘解代入式(16)可得式(17)。證明完畢。
4 結(jié)束語(yǔ)
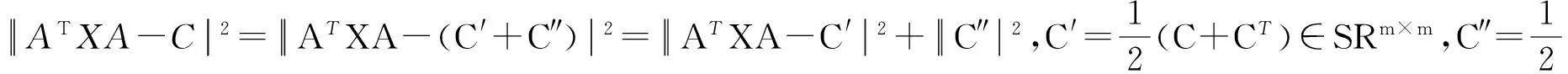
[1] 彭向陽(yáng),胡錫炎,張磊.矩陣方程的M-對(duì)稱解[J].數(shù)學(xué)學(xué)報(bào),2006,49(4):941-948.
PENG Xiangyang,HU Xiyan,ZHANG Lei.The M- Symmetric Solution of the Matrix Equation[J].Acta Mathematica Sinica,2006,49(4):941-948.
[2] JOSEPH K T.Inverse eigenvalue problem in structural design[J].Aiaa Journal,2012,30(30):2890-2896.
[3] XU W R,CHEN G L.Inverse problems for (R,S)-symmetric matrices in structural dynamic model updating[J].Computers & Mathematics with Applications,2016,71(5):1074-1088.
[4] YUAN Y,DAI H.Inverse problems for symmetric matrices with a submatrix constraint[J].Applied Numerical Mathematics,2007,57(5):646-656.
[5] LIAO A P,LEI Y.Least-squares solutions of matrix inverse problem for bi-symmetric matrices with a submatrix constraint[J].Numerical Linear Algebra with Applications,2010,14(5):425-444.
[6] DAI L F,LIANG M L.Generalized Inverse Eigenvalue Problem for (P,Q) Conjugate Matrices and the Associated Approximation Problem[J].Wuhan University Journal of Natural Sciences,2016,21(2):093-098.
[7] LI J F,Hu X Y,ZHANG L.Inverse problem for symmetric P-symmetric matrices with a submatrix constraint[J].Bulletin of the Belgian Mathematical Society Simon Stevin,2010,17(4):661-674.
(責(zé)任編輯 陳 艷)
SymmetricMSymmetric Optimal Approximation Solution of Matrix EquationATXA=C
XU Yu-xia, LEI Ying-jie, HOU Qiang
(School of Science,North University of China,Taiyuan 030051, China)
In the dynamic model updating, it usually needs to modify the stiffness matrix and the mass matrix to satisfy the orthogonal conditions. In this paper, they are modified by the study of their least-squares approximations. Then we obtain the symmetricMsymmetric least square solution’s ofATXA=Cby using canonical correlation decomposition in the symmetricMsymmetric matrices set; Based on this, by using the projection theorem and the generalized singular value decomposition, we get its symmetricMsymmetric optimal approximation solution of a given matrix.
symmetricMsymmetric matrices; projection theorem; canonical correlation decomposition; least square solution; optimal approximation solution
2016-12-18 基金項(xiàng)目:國(guó)家自然科學(xué)基金青年基金資助項(xiàng)目(11501528)
徐玉霞(1991—),女,河北衡水人,碩士研究生,主要從事組合矩陣?yán)碚摷捌鋺?yīng)用的研究,E-mail:1554760759@qq.com。
徐玉霞,雷英杰,侯強(qiáng).矩陣方程ATXA=C的對(duì)稱M對(duì)稱最佳逼近解[J].重慶理工大學(xué)學(xué)報(bào)(自然科學(xué)),2017(3):143-150.
format:XU Yu-xia, LEI Ying-jie, HOU Qiang.SymmetricMSymmetric Optimal Approximation Solution of Matrix EquationATXA=C[J].Journal of Chongqing University of Technology(Natural Science),2017(3):143-150.
10.3969/j.issn.1674-8425(z).2017.03.022
O175.13
A
1674-8425(2017)03-0143-08

