水電機組基于貝葉斯網絡的故障樹故障診斷分析研究

胡勇健，肖志懷

(1.深圳蓄能發電有限公司，深圳 518115；2.武漢大學動力與機械學院，武漢 430072)

0 引 言

由于組成構件之間及構件內部存在很多不確定關系，各種可能的因素充斥其間，使得故障診斷在大型設備領域應用中準確率比較低下，導致故障原因不易確定。因此如何從眾多不確定信息中獲得最終的最有可能的故障原因是故障診斷領域發展所需要克服的主要問題。

目前利用故障樹分析法建造模型進行故障診斷是最常用的，但這種模型卻存在一些局限性，表現為：處理不確定性問題能力有待提高、多源信息表達與融合能力相對較弱。然而近年來受到越來越多關注和研究的貝葉斯網絡，不僅從其推理機制和系統狀態描述看，與故障樹存在很大的相似之處；而且還可以描述事件之間不確定的故障邏輯關系，事件狀態多樣性的能力；并且貝葉斯網絡特有的雙向推理機制在故障診斷分析中具有明顯優勢[1]。因此，許多專家學者對貝葉斯網絡都進行了相關研究：文獻2將基于貝葉斯網絡的故障樹應用到機械設備中，文獻3研究了基于故障樹的貝葉斯網絡建造方法與故障診斷應用，文獻4研究了基于故障樹與貝葉斯網絡的鉆井井塌事故的定量分析，文獻5研究了基于故障樹貝葉斯網絡的裝備故障診斷方法，文獻6利用故障樹與貝葉斯網絡對采煤機進行了故障可靠性分析。

與采用貝葉斯網絡方法相比，如果采用故障樹分析方法計算系統的事件發生概率，首先需要進行定性分析得到該系統所有的最小割集，然后再利用容斥定理進行精確計算，或用獨立近似方法進行近似計算[7]，過程比較繁瑣；而采用貝葉斯網絡模型中的概率推理則可以在獲取網絡模型結構中節點間的相互影響程度后，直接利用貝葉斯網絡原理進行數學計算，用概率的形式表達和比較各個節點在系統出現故障時產生影響的程度，確定導致系統故障的可能原因。

本文將貝葉斯網絡引入到水輪發電機系統故障診斷模型中，利用貝葉斯網絡模型反向推理機制結合桶排除法給出發電機故障后驗概率的計算方法，并通過簡單算例比較貝葉斯網絡和故障樹分析算法，驗證該算法計算結果的有效性，最后通過計算發電機故障后驗概率與先驗概率的對比，給出故障時各個事件概率變化情況進行診斷，驗證貝葉斯網絡方法的可行性和合理性。

1 故障樹分析法與貝葉斯網絡模型

1.1 故障樹分析法

故障樹分析法是一種圖形演繹由果到因、自上而下的邏輯分析方法，通過分析可能造成目標故障的各種因素，畫出邏輯圖形成故障樹展示目標與因素之間的內在聯系，再對目標系統中實際發生的故障事件，做出由頂至底按樹狀逐級細化的分析。其目的是判明基本故障、確定故障原因、故障影響和發生概率等，是一種簡單可靠而又行之有效的系統故障診斷方法[8]。其過程可概括為：從某一故障事件開始，找出導致該事件發生的各個直接因素，然后對找出的因素分別尋找其各自的直接原因，重復執行該過程，直至把形成設備故障的基本事件分析出來為止[9]。依照此方法分析系統發生故障的各種途徑和影響因素，然后對各基本事件賦予概率值，就可以用故障樹模型進行診斷決策。故障樹結構由3種符號構成：事件符號、邏輯門符號、轉移符號。事件符號用于表示各種頂事件、中間事件和底事件；邏輯門符號用于表示各事件之間的邏輯關系；轉移符號則主要是為使圖形簡明、避免重復繪圖而設置的符號。應用故障樹模型一般需要做出假設：

(1)事件只有兩種狀態，即正常或故障；

(2)各個事件是彼此獨立的，不會產生相互間的影響聯系，即事件間存在條件獨立性；

(3)故障和導致該故障的因素連接關系是通過邏輯門來表達的，包括與門(AND)、或門(OR)、非門(NOT)、異或門(XOR)等。

簡單的故障樹結構如圖1所示。

圖1 簡單的故障樹結構Fig.1 Simple fault tree structure

1.2 貝葉斯網絡模型

貝葉斯網絡是一種基于網絡結構的有向圖解描述，用具有網絡結構的有向圖表達各個信息要素之間的關聯關系：用節點表示各個事件要素，用連接節點之間的有向邊表示各個事件要素的關聯關系，用條件概率表示各個事件要素之間的影響程度[10,11]。貝葉斯網絡本身將多種事件關聯關系可視化為一種概率依賴圖形模型，更加直觀的表明事件變量之間的因果和連接強度；同時貝葉斯網絡可在不完整的有限的信息條件下進行推理和學習，在解決不確定性問題方面具有很大的優勢。總的來看，貝葉斯網絡理論方法運用了一種反復學習的思想，首先使用通過領域專家知識指定的先驗概率表示節點間的不確定性關聯關系和連接強度，并將后來獲取到的數據進行處理，利用概率規則來對之前已經指定的先驗概率重新調整，使之更加貼合實際情況。

貝葉斯網絡模型描述的隨機變量間概率依賴關系，可表示為二元組B=，包括兩部分：

(1) 具有n個節點的有向無環圖G。G=是一個有向圖網絡結構，其結點為X={x1,x2,…,xn}，n≥1，A是弧的集合。網絡結構中節點代表事件變量，節點間的弧A代表相互關聯關系；

(2)節點相關的條件概率表P。條件概率可以用p(Vi|Pa(Vi))(Pa(Vi)是Vi的父結點，在G中的兩個相互連接的節點對A→B中，A稱為B的父節點，B稱為A的子節點)來表示。結構中任意節點的任何一種概率都可以看作是在一定先驗知識下的條件概率。

(1)

式中：p(A)為A的先驗概率；p(A/B)為A的后驗概率。 先驗概率往往是根據以往的經驗分析總結得到的概率，后驗概率指在獲得一定的事實條件信息下對節點概率進行修正后的概率。

如果A存在n種狀態a1,a2,…,an，那么貝葉斯網絡的全概率公式定義:

p(B)=∑p(B/A-ai)p(A=ai),i=1,2,3,…,n

(2)

2 故障樹與貝葉斯網絡模型的比較

2.1 故障樹轉化貝葉斯網絡模型方法

比較發現貝葉斯網絡與故障樹的組成結構是相互對應的，根據故障樹的結構，可以將故障樹轉換成貝葉斯網絡模型：故障樹中每個基本事件和邏輯門輸出事件對應貝葉斯網絡的各層節點，邏輯門對應連接葉斯網絡的各層節點的有向邊，故障樹的邏輯關系可以通過改變貝葉斯網絡的條件概率表來實現表達[12]。具體的轉化對應關系如圖2所示。

圖2 故障樹與貝葉斯網絡模型對應關系Fig.2 Correspondence between fault tree and Bayesian network model

現以圖3所示的簡單故障樹結構為例進行說明，轉化后的貝葉斯網絡模型及相關的邏輯連接關系如圖4所示，假設故障樹中各設備的狀態只有兩種：正常(0)和故障(1)。

圖3 與或門故障樹Fig.3 Gate fault tree

圖4 轉化后的貝葉斯網絡圖Fig.4 Transformed Bayesian Networks

2.2 故障樹與貝葉斯網絡分析方法對比

以圖3和圖4為例，利用故障樹方法和貝葉斯網絡方法計算兩種模型相同頂層事件 的故障發生概率，假設：

p(X1)=(0.95，0.05)

p(X2)=(0.92，0.08)

p(X3)=(0.91，0.09)

(1)故障樹方法：根據最小割集定義，分析得出此簡單系統的最小割集為{X1,X3},{X2,X3}，運用不交化原理的計算過程可以得到頂事件T=1的發生概率為：

p(T=1)=p(X1=1)·p(X3=1)+p(X2=1)·p(X3=1)-

p(X1=1)·p(X2=1)·p(X3=1)=0.011 34

(3)

(2)貝葉斯網絡方法：根據貝葉斯網絡全概率公式可知，頂層事件T=1的全概率公式為：

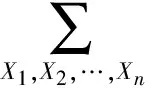
(4)

結合圖3故障樹模型經轉化至貝葉斯網絡模型圖4中的“與、或”關系，可以得到：

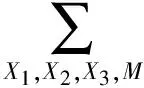
p(X3=1)·[1-p(X1=0)·p(X2=0)]=0.011 34

(5)

比較式(3)和式(5)，顯然這兩種計算方法的過程存在差異，結果相同。如果對一些結構復雜、邏輯門多樣的故障樹進行分析時，采用故障樹分析法首先需要找出系統所有最小割集再運用不交化原理進行計算，是一個繁瑣的計算過程；然而將其轉化成貝葉斯網絡模型后就可以運用條件概率公式和全概率公式計算獲得頂事件的發生概率，避免了最小割集的求解，分析過程將變得較為方便簡單。

3 發電機故障診斷分析

水輪發電機是將水的機械能轉化為電能的重要機組設備，在運行時受到眾多因素的影響，容易導致故障的發生，所產生的故障又大多是相互關聯、相互影響的，因此難以有效分析確定出故障發生的原因。通過總結實際運行中的發電機故障，常出現以下幾種類型的故障：定子機座振動、定子鐵芯及繞組故障引起的定子故障；轉子鐵芯及繞組引起的轉子故障；發電機電磁不平衡以及轉子質量不平衡引起的發電機動不平衡；轉頻及極頻振動引起的電磁振動。在對水輪發電機的各種故障機理進行分類后，按照一定的邏輯門關系構建了一個簡單的由“或門”連接的水輪發電機故障樹結構。其故障樹結構如圖5所示：

圖5 發電機故障樹結構模型Fig.5 Generator fault tree model

假設故障樹結構中各個底層事件之間是相互獨立不產生相互影響的，并且整個系統和系統中所包含的事件都只有兩種狀態：正常(0)和故障(1)。根據專家系統獲得各個底層事件的先驗概率分布為：

p(X1)=(0.980 4，0.019 6)

p(X2)=(0.998 7，0.001 3)

p(X3)=(0.993 5，0.006 5)

p(X4)=(0.995 7，0.004 3)

p(X5)=(0.995 5，0.004 5)

p(X6)=(0.994 4，0.005 6)

p(X7)=(0.996 4，0.003 6)

p(X8)=(0.997 7，0.002 3)

p(X9)=(0.998 6，0.001 4)

依據圖2所示的轉化對應關系將圖5所示的發電機故障樹模型結構轉化為貝葉斯網絡模型結構，建立發電機故障貝葉斯網絡結構模型如圖6所示，其中同一層的節點均是通過“或門”與上一層節點相連接。

圖6 轉化后的貝葉斯網絡模型Fig.6 Transformed Bayesian network model

利用桶排除法，結合貝葉斯網絡的正向推理能力、全概率公式和貝葉斯網絡節點之間的相互聯系可以計算出頂層事件“發電機故障T”的發生概率:

p(S1=0)=p(X1=0)·p(X2=0)·p(X3=0)=0.972 8

p(S1=1)=1-p(S1=0)=0.027 2

同理可以求得

p(S2)=(0.991 2，0.008 8)

p(S3)=(0.990 8，0.009 2)

p(S4)=(0.996 3，0.003 7)

p(T)=(0.951 8，0.048 2)

即在此種專家系統確定的系統底層各個事件故障概率情況下，系統頂層節點發電機發生故障的可能性為0.048 2。

同時貝葉斯網絡又具有反向推理的能力，可以算得在整個系統頂層節點發電機出現故障的情況下底層各個節點的后驗概率分別為：

p(X1=1/T=1)=

0.406 6

p(X2=1/T=1)=0.027 0

p(X3=1/T=1)=0.134 9

p(X4=1/T=1)=0.089 2

p(X5=1/T=1)=0.093 4

p(X6=1/T=1)=0.116 2

p(X7=1/T=1)=0.074 7

p(X8=1/T=1)=0.047 7

p(X9=1/T=1)=0.029 0

將計算獲得的各個底層節點的后驗概率與先驗概率進行柱狀圖分析，結果如圖7所示。

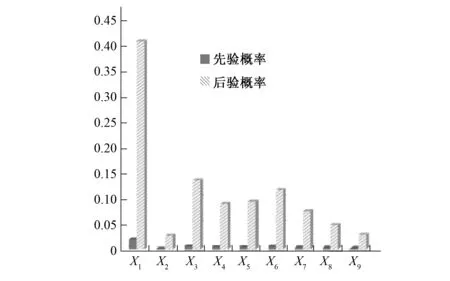
圖7 各底層節點的先驗概率與后驗概率對比Fig.7 Comparison of the prior probability and the posterior probability of each node

由圖7可以看出，當系統發生故障時，節點X1即定子繞組故障的后驗概率變化最為顯著，其他的X3節點和X6節點變化也較大，因此在此種專家系統確定的各個節點的先驗概率條件下，如果發電機系統出現了故障，首先需要查看的節點即為X1定子繞組故障。當然此種診斷推理結果會一定程度上依賴專家系統確定的先驗概率情況，但依舊可以說明故障樹模型結構轉化為貝葉斯網絡模型在復雜故障診斷領域的可行與合理性。

5 結 論

通過簡單與或門故障樹算例，驗證了貝葉斯網絡正向推理方法與故障樹分析方法的計算結果是相同的，然后將貝葉斯網絡引入到發電機故障診斷分析中，其核心是將故障樹轉化建立貝葉斯網絡模型，利用貝葉斯網絡全概率公式和條件概率公式反向推理，用概率的形式表示出系統發生故障時各部件故障的可能性，對比之前通過專家系統確定的先驗概率，得到最有可能發生故障的底層事件，據此對系統故障進行診斷，對大型復雜系統的故障診斷具有指導意義。

□

[1] 張曉丹. 汽車發動機故障診斷中不確定性問題的貝葉斯網絡解法[D]. 東北大學, 2005.

[2] 楊 虹, 汪厚祥, 支冬棟,等. 基于貝葉斯網絡的故障樹在機械設備中的應用[J]. 微計算機信息, 2010,26(4):115-117.

[3] 李儉川, 胡蔦慶, 秦國軍,等. 基于故障樹的貝葉斯網絡建造方法與故障診斷應用[J]. 計算機工程與應用, 2003,39(24):225-228.

[4] 李 盼, 樊建春, 劉書杰. 基于故障樹與貝葉斯網絡的鉆井井塌事故的定量分析[J]. 中國安全生產科學技術, 2014,(1):143-149.

[5] 齊善明, 李 磊, 楊 歡. 基于故障樹貝葉斯網絡的裝備故障診斷方法研究[J]. 艦船電子工程, 2012,32(6):112-114.

[6] 古海龍, 劉混舉. 基于故障樹與貝葉斯網絡的采煤機故障可靠性分析[J]. 煤炭技術, 2015,34(3):242-244.

[7] 陳東寧, 姚成玉, 王 斌. 貝葉斯網絡在液壓系統可靠性分析中的應用[J]. 液壓與氣動, 2012,(7):58-61.

[8] 宮義山, 高媛媛. 基于故障樹和貝葉斯網絡的故障診斷模型[J]. 沈陽工業大學學報, 2009,31(4):454-457.

[9] 張 燕, 佘 維, 李 平. 基于Petri網和故障樹的電力系統故障診斷模型[J]. 計算機測量與控制, 2015,23(8):2 626-2 628.

[10] Stephenson T A.An introduction to Bayesian network theory and usage[R].Swizerland: IDIAP-RR 00-03,DaleMolle Institute,2000.

[11] Bresnick T A, Buede D M, Tatman J A. Introduction to Bayesian network[C]∥The 66th MORS Symposiam, California; Naval Postgraduate School Monterey, 1998:23-25.

[12] 周忠寶, 周經倫, 金 光,等. 基于貝葉斯網絡的概率安全評估方法研究[J]. 系統工程學報, 2006,21(6):636-643.