浮式垂直軸風機的動力學建模、仿真與實驗研究1)

劉利琴郭 穎 趙海祥 唐友剛

(天津大學水利工程仿真與安全國家重點實驗室，天津300072)

浮式垂直軸風機的動力學建模、仿真與實驗研究1)

劉利琴2)郭 穎 趙海祥 唐友剛

(天津大學水利工程仿真與安全國家重點實驗室，天津300072)

考慮氣動力和水動力的耦合研究浮式垂直軸風機系統的運動響應，將固定式垂直軸風機的氣動載荷計算方法進一步推廣到海上浮式垂直軸風機的氣動載荷計算.考慮阻尼力、波浪力、風載荷、系泊力等，建立了浮式垂直軸風機系統的縱蕩--垂蕩--縱搖運動方程.考慮動態失速和浮式基礎運動，基于雙致動盤多流管理論，推導了風機葉片氣動載荷計算公式，編制了數值計算程序.以Sandia 17m風機為例，驗證了氣動載荷計算程序的正確性.最后進行了模型實驗，其中模型的風機為Φ型達里厄垂直軸風機，支撐基礎為桁架式Spar型浮式基礎，將模型實驗結果與數值計算結果進行了對比，驗證了耦合計算程序.結果表明，數值計算得到的風機系統的垂蕩、縱搖運動的RAO(幅值響應算子)曲線與模型實驗結果吻合較好，驗證了耦合程序的正確性.然而，由于數值計算與模型實驗在運動自由度、阻尼、風載荷等方面存在差別，數值計算結果與模型實驗結果仍有一定的差異.

浮式垂直軸風機,氣動力--水動力耦合，數值模擬,模型實驗

引言

隨著單機功率的增加(從30年前的50kW增至目前的5MW以及計劃中的10MW～20MW)，海上浮式風機的尺寸越來越大.置于水平軸風機頂部的巨大傳動系統造成了風機系統的不穩定，其大型化發展受到制約.而垂直軸風機的傳動系統位于風機底部，不會對風機塔架造成影響，這使得垂直軸風機在海上風電的大型化發展中具有更大的優勢[1].

各國學者針對水平軸風機開展了大量的研究，例如浮式水平軸風機氣動載荷、不同浮式基礎支撐下風機系統的運動、浮式風機系統的氣動力與水動力的耦合等[2-5].相對而言，目前關于浮式垂直軸風機系統的研究較少.Cahay等[6]概念性地設計了安裝于半潛式平臺的三葉片2MW達里厄型風機模型. Vita[7]研究并分析了Spar型5MW垂直軸風機的可行性.Blusseau等[8]在頻域中分析了陀螺效應對半潛式垂直軸風機運動的影響.Cheng等[9]分析了Spar型、半潛型和張力腿(TLP)型三種不同浮式基礎支撐的垂直軸風機的運動響應.研究發現，由于TLP型垂直軸風機的2P(2倍轉子頻率)氣動力對整個浮式風機系統的運動影響顯著，因此TLP型浮式基礎不適合支撐垂直軸風機.Collu等[10]采用FloVAWT程序研究了浮式垂直軸風機6個自由度的運動響應，并分析了氣動力、浮式基礎水動力以及系泊力對風機系統運動的影響.

針對浮式水平軸風機，目前已開發了大量的商業計算軟件，如Fast/Aerodyn/Hydrodyn,Adms,Bladed, 3Dfloat Simo/Rifl x/Hawc2等[11-15]都廣泛應用于海上浮式水平軸風機的設計、計算中.Berg等[16-18[19]、改進的Hawc2[7]、Simo-Rifl x-DMS[20]以及美國圣地亞國家實驗室開發的剛柔耦合程序[21]，這些程序主要用于內部計算.關于浮式垂直軸風機系統的動力響應、氣動力--水動力--系泊力--結構動力的耦合特性及動力控制等方面，還需要進一步研究.

本工作研究浮式垂直軸風機的運動響應，考慮氣動力和水動力的耦合，建立了浮式垂直軸風機系統縱蕩--垂蕩--縱搖運動微分方程.考慮動態失速[18]和浮式基礎運動，推導了垂直軸風機的氣動載荷計算公式，編制了計算程序并對程序進行了驗證.

1 浮式垂直軸風機系統運動微分方程

1.1 耦合運動方程

將整個浮式垂直軸風機系統處理為剛體，考慮慣性力(矩)、阻尼力(矩)、回復力(矩)、系泊力、風載荷和波浪載荷，參考深水Truss Spar平臺的運動方程[22-23]，得到浮式風機系統的縱蕩--垂蕩--縱搖耦合運動微分方程為

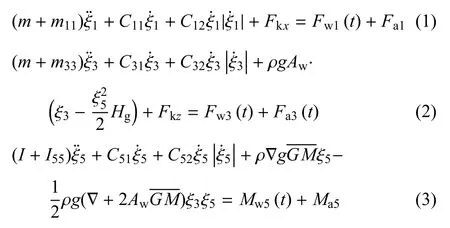
式中，ξ1,ξ3和ξ5分別為風機系統的縱蕩、垂蕩和縱搖位移；m為風機系統的質量；m11和m33分別為縱蕩和垂蕩附加質量；I為風機系統的縱搖轉動慣量，I55為縱搖附加轉動慣量；C11,C31和C51分別為風機系統的縱蕩、垂蕩和縱搖一階阻尼；C12,C32和C52分別為風機系統的縱蕩、垂蕩和縱搖二階阻尼；Aw為浮式基礎的水線面面積，為風機系統的縱穩性高，?為排水體積，ρ為海水密度；Fw1(t)和Fw3(t)分別為作用于浮式基礎的縱蕩和垂蕩波浪力，Mw5(t)為作用于浮式基礎的縱搖波浪力矩；Fkx和Fkz分別為作用于風機系統縱蕩和垂蕩方向上的系泊力；Fa1和Fa3分別為作用于風機系統縱蕩和垂蕩方向上的風載荷，包括氣動載荷和風壓載荷；Ma5為作用于風機系統縱搖方向上的風傾力矩，包括氣動載荷和風壓載荷產生的力矩.

1.2 浮式風機氣動載荷

1.2.1 速度矢量關系

基于雙致動盤多流管理論[24]計算作用于葉片上的氣動載荷.將整個浮式風機系統處理成剛體，考慮動態失速及浮式基礎縱蕩、垂蕩、縱搖運動位移和速度的影響進行推導.

將流管分為上風區和下風區，分別計算上、下風區浮式基礎的運動對流管內速度的影響.風機系統的坐標及速度矢量關系如圖1所示.浮式風機運動的坐標原點取為整個風機系統的重心，縱蕩和垂蕩運動的正方向分別沿x軸和z軸(圖1(a))正方向，縱搖運動的正方向為順時針方向.

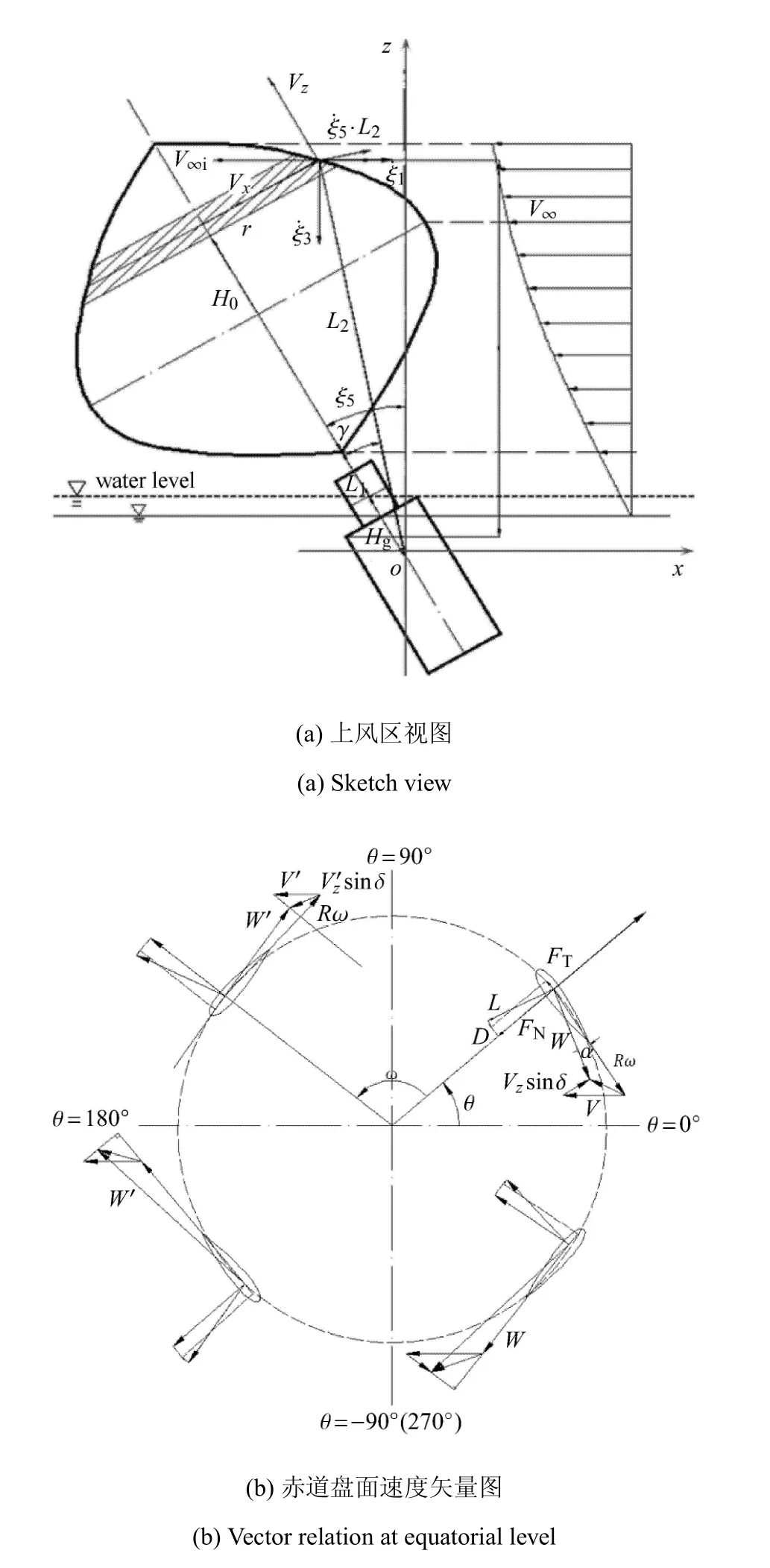
圖1 風機系統坐標和速度矢量關系圖Fig.1 Coordinate system and vector relation of the wind turbine

考慮平均風速，即風速為水平面以上高度的函數.對于局部高度zi，風速可由下式表示

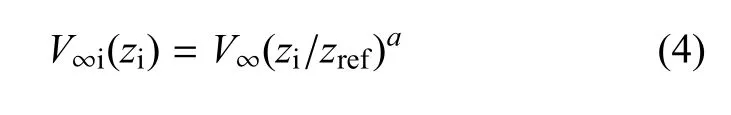
式中，V∞為參考高度zref處的平均風速，zref取葉片中心到水面的距離，a=0.14[25].

假定平行于流管方向的速度僅影響誘導速度，垂直于流管方向的速度只對局部合速度產生影響.對于上風區，葉片局部到浮式風機重心的距離由下式表示

式中，r為風機局部半徑，θ為轉子的方位角，H0為每個流管到葉片底部的距離，L1為靜止時葉片底部到水平面的距離，Hg為靜止時風機系統的重心到水平面的距離.葉片局部位置與塔柱之間的夾角可表示為

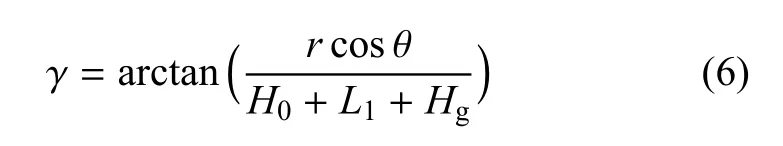
葉片局部位置來流風速可表示為

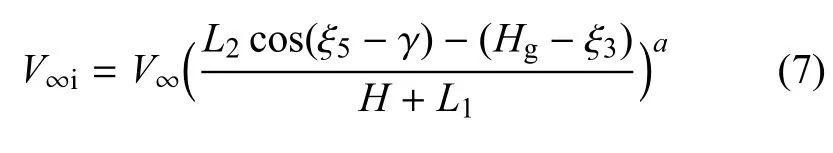
式中，H為葉片半高.平行和垂直于塔柱方向的流管局部合速度可分別表示為

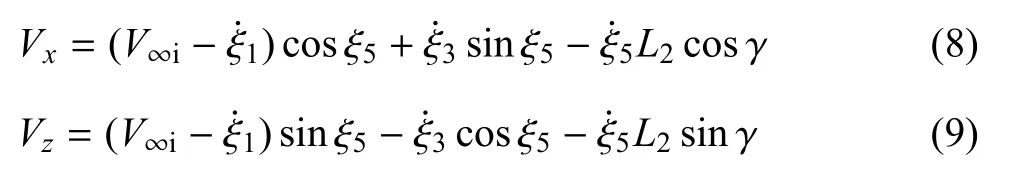
基于類似的推導，可得到下風區平行和垂直于流管方向的合速度為

式中，u＜1為上風區的干擾因子.

1.2.2 作用于葉片上的力和力矩

上、下風區的誘導速度V和V′可分別由下式確定

式中，u′為二次干擾因子.

對于上風區轉子，即方位角 θ 的范圍為[-π/2,π/2]，局部相對速度可由下式表示

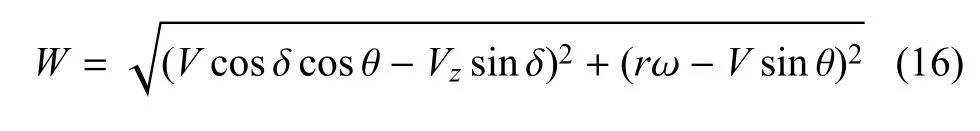
式中，δ為葉片法向面與赤道平面的夾角，ω為葉片的旋轉速度.

局部攻角可由下式確定

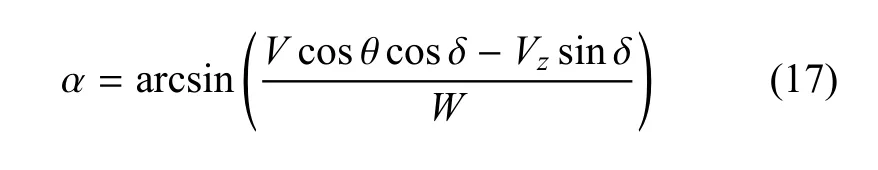
將上風區的方位角θ等分為若干個角管，每個角管大小為?θ.假設在每個角管內，誘導速度為常數，即每個角管內的干擾因子為常數，并表示為

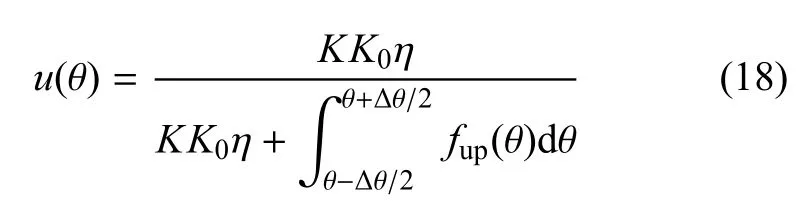
式中，η=r/R，R為赤道處葉片半徑.K，K0和f(θ)的表達式分別為

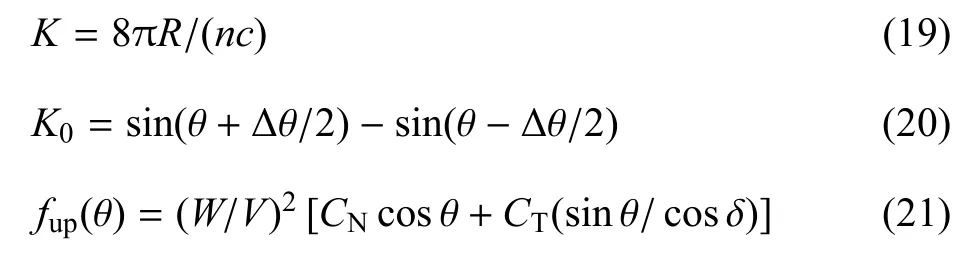
式(19)中，n為葉片數量，c為弦長.式(21)中，CN和CT分別為局部葉素法向力系數和切向力系數，由下式確定

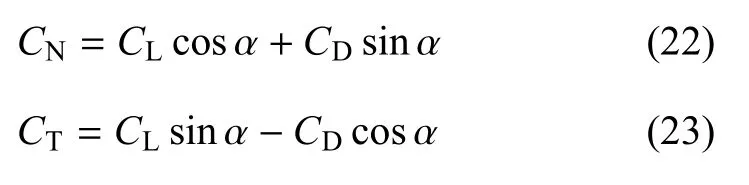
式中，CL和CD分別為升力系數和阻力系數，根據局部雷諾數和局部攻角由實驗數據[24]插值，并采用Gormont-Berg動態失速模型[26]修正后得到.

局部雷諾數可表示為

對于給定的轉子幾何型線、轉速以及各流管來流速度，假定干擾因子初值u(θ)=1，可通過式(14)～式(24)進行迭代計算，得到最終的干擾因子，進而確定切向力系數CT和法向力系數CN.

葉片法向力FN和葉片切向力FT均可表示為葉片位置θ的函數，對處于上風區的轉子，FN和FT可表示為

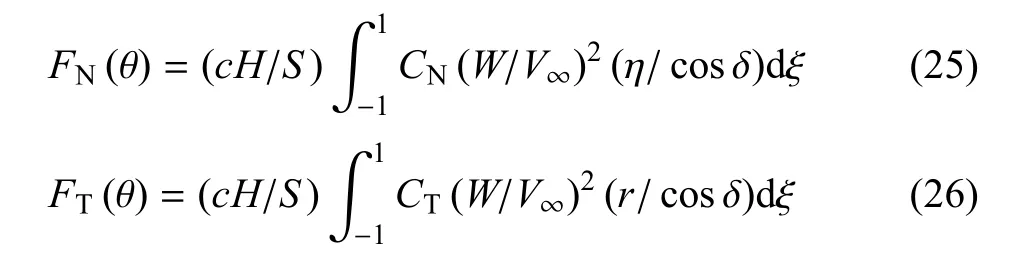
式中，S風機葉片的掃掠面積.

與式(26)對應的無因次切向力系數為

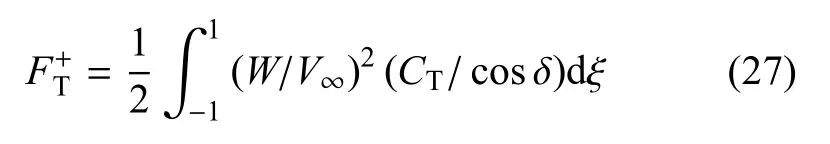
根據各葉素的旋轉中心計算扭矩，將各葉素扭矩沿葉片型線積分，得θ處葉片整體扭矩為

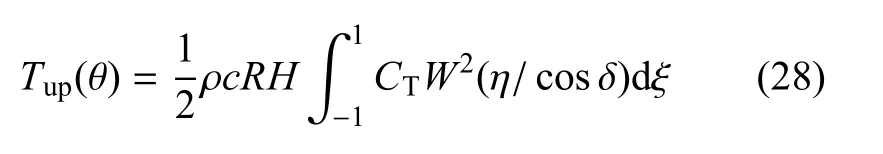
轉子上風區功率系數的表達式為

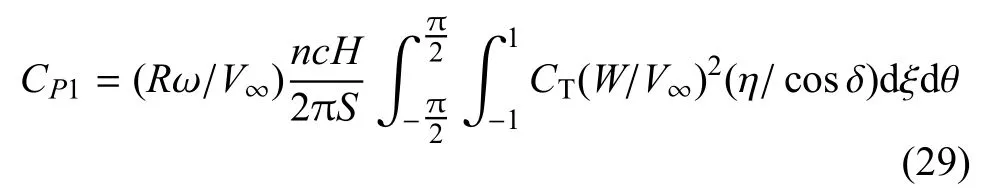
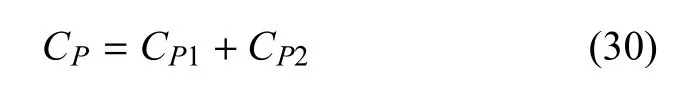
將法向力和切向力分解，可得到作用于浮式風機垂蕩和縱蕩方向的升力和推力；對重心取矩，可得到作用于浮式風機系統縱搖運動的氣動力矩.將以上計算得到的氣動力(矩)代入系統運動方程(1)～方程(3)，可進一步分析浮式風機系統在時域內的運動響應.

1.3 浮式基礎水動力計算

浮式基礎的水動力參數由 Sesam/Wadam 軟件[27]計算.計算中風機處于停機狀態，不考慮風載荷和系泊，僅考慮風機的質量和形狀的影響.根據結構尺寸將浮式基礎模型劃分為面元模型和莫里森模型.面元模型基于勢流理論計算大尺寸構件的水動力[28]，莫里森模型基于莫里森方程計算小尺寸構件的水動力[28].

用Wadam計算波浪力(矩)和附加質量(附加轉動慣量)傳遞函數，將計算所得結果代入方程(1)～方程(3)進行時域響應計算.

1.4 風壓載荷計算

根據API規范[29]計算作用于塔柱和葉片(停機狀態)上的定常風壓和風傾力矩，公式如下

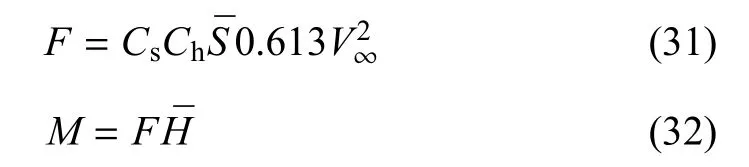
式中，Cs為受風構件的形狀系數，Ch為受風構件的高度系數，為沿風向受風構件的投影面積，為風載荷作用位置到風機系統重心的距離，V∞的定義見式(4).

1.5 浮式基礎阻尼和系泊系統

垂蕩板降低浮式風機垂蕩運動，增加垂蕩附加質量，同時可能改變浮式風機系統的垂蕩固有周期.在運動響應計算中，系統的黏性阻尼十分重要，可通過CFD方法或模型實驗得到.

考慮懸鏈線系泊，導纜孔的位置在浮式風機的重心附近，采用準靜態懸鏈線方法[30]計算作用在浮式風機系統縱蕩和垂蕩運動的系泊力.

采用四階龍格庫塔方法求解方程 (1)～方程(3)，得到時域運動的數值解.

1.6 計算程序

計算程序包含兩個模塊，一個模塊計算風機的氣動載荷，另一個模塊計算浮式風機系統的運動.在每個時間步，考慮風機運動計算氣動力(矩)；考慮氣動力(矩)、波浪力(矩)、系泊力(矩)、定常風壓載荷等計算浮式風機系統的運動；然后根據新的位移和速度，計算氣動力(矩).重復以上過程，最終求得氣動力和水動力耦合的運動響應.具體的計算流程如圖2所示，采用MATLAB軟件編寫計算程序.

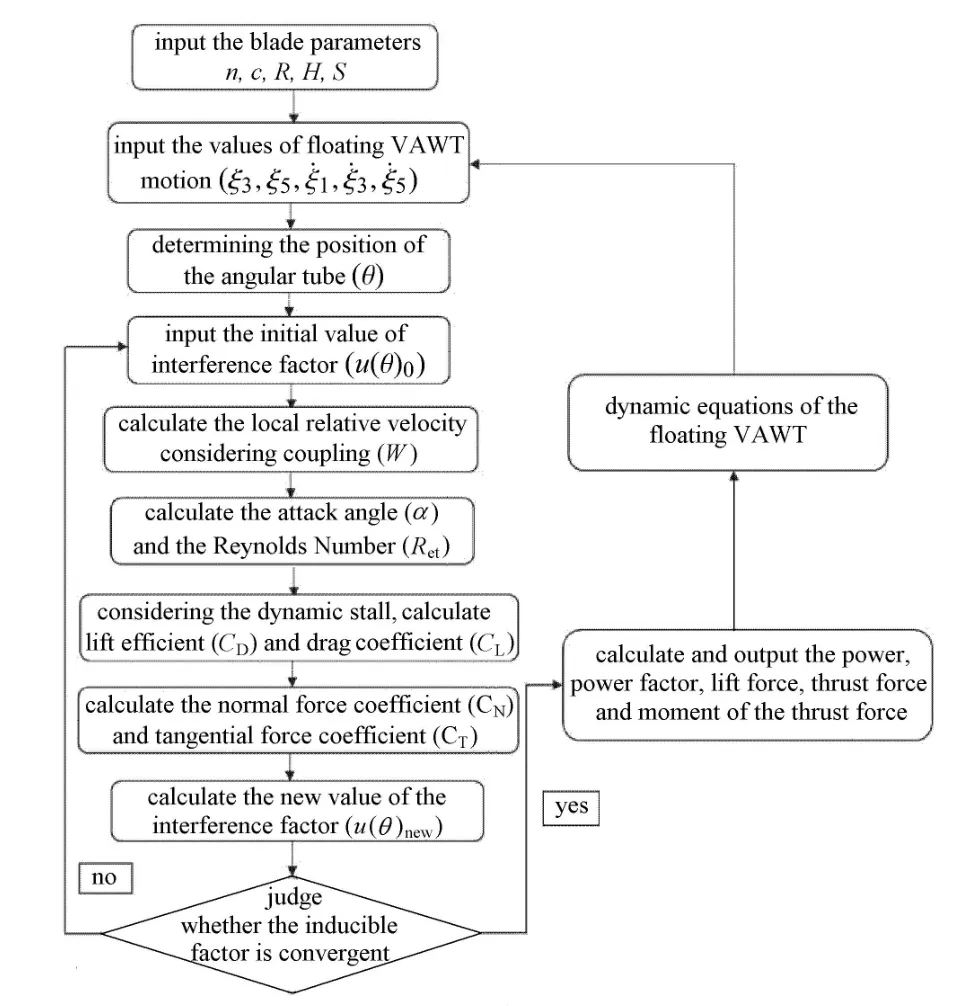
圖2 計算流程圖Fig.2 Computing process

2 氣動載荷計算程序驗證

本節僅對氣動載荷程序進行驗證，不考慮氣動載荷和浮式風機運動的耦合.以Sandia 17m風機為例[31]，計算風機功率和葉片的無因次切向力系數，并與Paraschivoiu的計算結果[31]進行對比，結果如圖3所示.

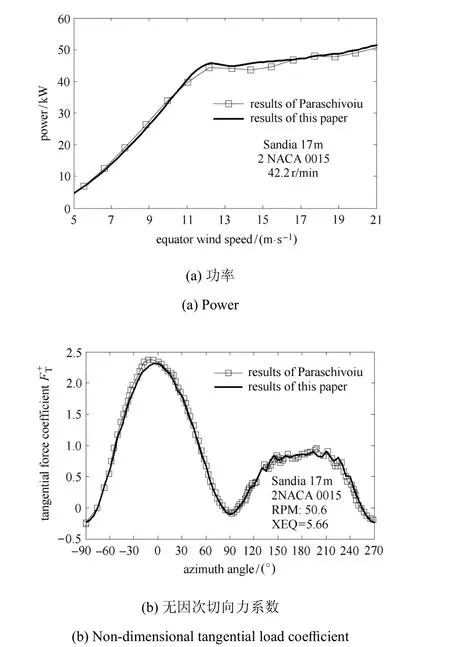
圖3 氣動載荷計算程序驗證Fig.3 Validation of the aerodynamics computing code

從圖3可看出，本文計算結果與Paraschivoiu的計算結果吻合非常好，從而可以驗證本文氣動載荷計算程序的正確性.

3 數值仿真與實驗結果對比

本節將數值仿真結果與模型實驗結果進行對比，驗證耦合計算程序的正確性.模型實驗在天津大學船舶與海洋工程實驗水池進行，水池水深3m，寬7m，長137m.使用搖板造波機可得到波長為2m～12m之間的規則波.

3.1 浮式風機參數

以5MW浮式垂直軸風機為例開展實驗.浮式風機形式如圖4所示，其中，風機為達里厄型[7]；支撐基礎為桁架式Spar型，它由浮力艙、上部機械艙、桁架結構、垂蕩板和底部壓載艙組成，文獻[32]研究了該浮式基礎的水動力特性.在風載荷作用下，葉片帶動塔柱旋轉，通過置于上部機械艙的傳輸設備和發電裝置將機械能轉化為電能.

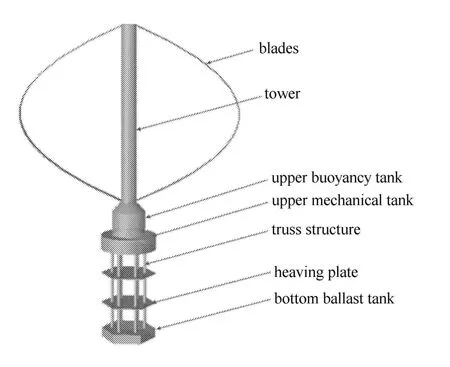
圖4 浮式風機Fig.4 The floatin VAWT

考慮到實驗水池的尺寸，選取縮尺比為1:70.該模型實驗滿足幾何相似、重力相似及動力相似(即斯特赫哈爾數相似)原則，模型參數見表1.

表1 模型參數Table 1Parameter of model

為滿足重量要求，葉片由特殊輕質木材制成，并滿足結構強度要求.為有效模擬風機旋轉，在風機底部安裝一個60W的電機來驅動風機.考慮模型結構的重量和形狀，根據縮尺比，調整風機系統模型的重量、重心位置和轉動慣量.

3.2 風場

由9個250W的風扇組成3×3的風扇矩陣模擬風場，并將其固定在拖車上.該風場可生成均勻分布的定常風.為得到穩定的氣流，在風扇矩陣前安裝了兩層整流罩.通過風速儀測量風速.文獻[33]對該風場進行了詳細的描述.

3.3 實驗方案

由于為便于安裝，在模型重心處布置4根帶有彈簧的系泊線以限制風機系統的水平位移，因而系泊系統的動態效應無法準確模擬.以下重點分析浮式風機的垂蕩和縱搖運動，系泊系統的影響較小.

采用浪高儀測量水池內的波浪高度，采用非接觸光學測量儀(包括LED燈，照相機，信號接收系統)測量模型的6自由度運動.將3個LED燈安裝在浮式基礎上端以測量模型的運動，將照相機固定于拖車軌道上，實際的實驗布置如圖5所示.

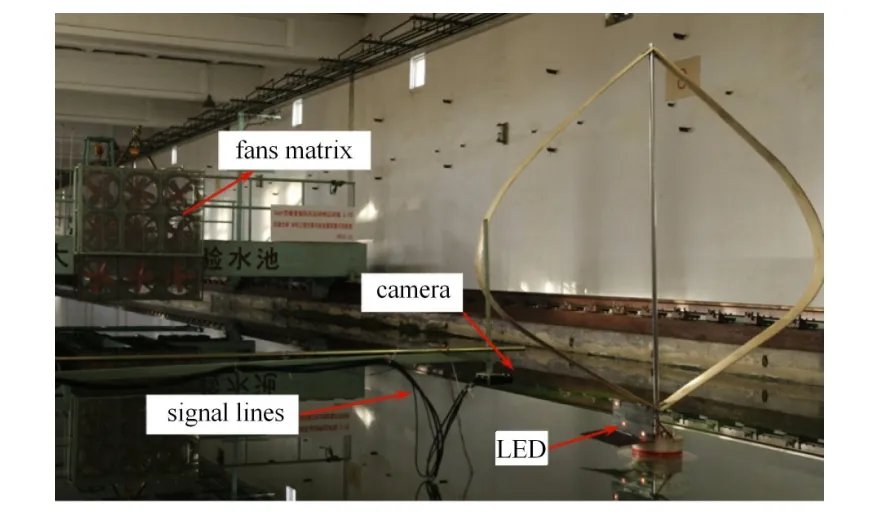
圖5 實驗布置圖Fig.5 The test layout

3.4 自由衰減運動實驗

在靜水中進行浮式風機垂蕩和縱搖的自由衰減實驗，不考慮波浪力和風力的作用.風機處于停轉狀態，轉子平面垂直于水池長度方向.

動力系統的一般自由衰減運動方程可表示為

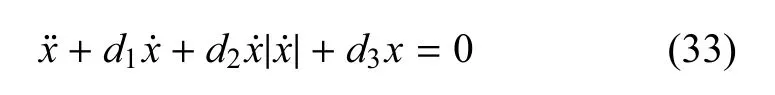
式中，d1是線性阻尼系數，d2為非線性阻尼系數.可用消滅曲線法[28]，通過自由衰減曲線計算得到d1和d2.最終的阻尼系數結果如表2所示，該阻尼系數將用于風機系統的數值模擬研究.

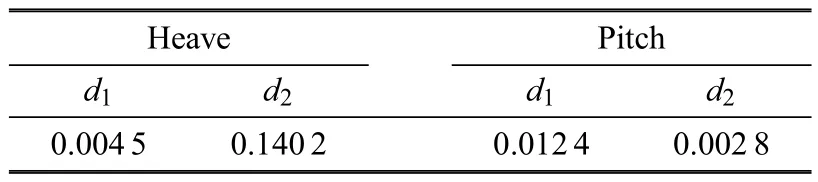
表2 浮式風機阻尼系數Table 2 Damping coefficient of the floatin VAWT

3.5 浮式風機系統動力學實驗

考慮風、浪聯合作用，進行風機模型動力學實驗.實驗中，波高為2m，波浪周期范圍為10～25s，風機轉速為5.26r/min(額定轉速)，風速為14m/s(額定風速).由非接觸光學運動測量儀可測得風機模型6個自由度的運動響應.

采用數值方法求解式 (1)～式 (3)，環境參數與實驗環境參數保持一致 (即波高 2m，波浪周期10s～25s，風速為14m/s，轉速為5.26r/min).計算得到浮式風機系統垂蕩和縱搖運動的RAO(幅值響應算子)曲線，并與實驗結果(根據縮尺比，將實驗數據轉換為對應的實型數據)進行對比，如圖6所示.

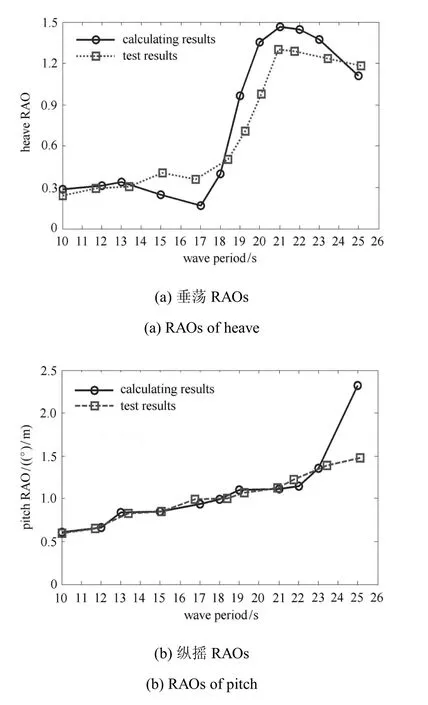
圖6 浮式風機垂蕩、縱搖RAO曲線Fig.6 RAO curves of heave and pitch of the floatin VAWT

3.6 結果分析

圖6表明，隨波浪周期的變化，數值計算和模型實驗得到的浮式風機系統的垂蕩、縱搖運動RAOs曲線的變化趨勢一致，驗證了耦合計算程序的正確性.

然而，在RAOs曲線的極值位置，例如垂蕩RAO曲線(數值模擬結果)的極大值和極小值處，數值模擬與模型實驗結果的差異明顯.造成差異的主要原因如下：

(1)運動自由度不同.模型實驗中，浮式風機的運動是6個自由度，而數值模擬中只考慮了垂蕩和縱搖兩個自由度.

(2)阻尼不同.數值方法中采用了風機停機狀態的阻尼系數，沒有考慮風機旋轉對系統阻尼的影響.而實際中，風機的旋轉對風機系統阻尼的影響非常復雜，在一定條件下具有顯著的增阻效應，該問題有待進一步深入研究.

(3)風壓載荷不同.在數值模擬中，風速是高度的函數；而在模型實驗中，由于風場的限制，整個風場內的風速是恒定的.

4 結論與討論

本文將固定式垂直軸風機的氣動載荷計算方法進一步推廣到海上浮式垂直軸風機的氣動載荷計算.考慮氣動力和水動力的耦合作用，研究浮式垂直軸風機系統動力學，主要結論概括如下：

(1)考慮動態失速和浮式基礎運動，推導了垂直軸風機葉片氣動載荷的計算公式.建立了浮式垂直軸風機系統的縱蕩、垂蕩、縱搖耦合運動微分方程，編制了數值計算程序.

(2)以Sandia 17m風機為例，計算了風機的功率和葉片的無因次切向力系數，通過與Paraschivoiu的計算結果[31]對比，驗證了氣動載荷計算程序的正確性.

(3)以5MW浮式垂直軸風機為例，開展了模型實驗，對比分析了數值仿真結果和模型實驗結果.研究表明，隨波浪周期的變化，數值計算和模型實驗得到的風機系統的垂蕩、縱搖運動的RAO曲線的變化趨勢一致，驗證了耦合計算程序的正確性.

本文研究還存在一些不足，如計算氣動載荷時尚未考慮湍流風和二次效應，沒有考慮塔柱和葉片的彈性變形；由于風場的限制，模型實驗只進行了額定風速的測試；在耦合計算程序驗證中，只考慮了垂蕩和縱搖運動，對縱蕩運動需要進一步驗證；由于數值計算和模型實驗在運動自由度、阻尼、風載荷等方面的差別，使得數值計算結果和模型實驗結果有一定的差異，以后將對該問題做進一步改進.

1 Willy T,Tjukup M,Sohif M,et al.Darrieus vertical axis wind turbine for power generation II:challenges in HAWT and the opportunity of multi-megawatt Darrieus VAWT development.Renewable Energy,2015,75:560-571

2 Madjid K,Torgeir M.Wave and wind induced dynamic response of a spar-type o ff shore wind turbine.Journal of Waterway Port Coastal and Ocean Engineering,2012,138:9-20

3 張亮,葉小嶸,吳海濤等.海上浮式風力機環境載荷及運動性能分析.太陽能學報,2013,34(5):876-881(Zhang Liang,Ye Xiaorong, Wu Haitao,et al.Analysis on environmental load and motion performance of floatin o ff shore wind turbine.ActaEnergiae Solaris Sinica,2013,34(5):876-881(in Chinese))

4 Ramachandran GKV,Bredmose H,Sorensen JN,et al.Fully coupled three-dimensional dynamic response of a tension-leg platform floatin wind turbine in waves and wind.Journal of Offshore Mechanics and Arctic Engineering,2014,136(2):1-12

5 Ma Y,Hu ZQ.Dynamic analysis for a spar-type wind turbine under di ff erent sea states//Proceedings of the ASME 2013 32th International Conference on Ocean,O ff shore and Arctic Engineering, Nantes,France,2013

6 Cahay M,Luquiau E,Smadja C.Use of a vertical wind turbine in an o ff shore floatin wind farm//Proceedings of the O ff shore Technology Conference,OTC-21705-MS,Houston,Texas,USA,2011

7 Vita L.O ff shore floatin vertical axis wind turbines with rotating platform.[PhD Thesis].Copenhagen,Denmark:Danish Technical University,2011

8 Blusseau P,Patel MH.Gyroscopic e ff ects on a large vertical axis wind turbine mounted on a floatin structure.Renewable Energy, 2012,46:31-42

9 Cheng ZS,Wang K,Gao Z,et al.Dynamic response analysis of three floatin wind turbine concepts with a two-bladed Darrieus rotor.Journal of Ocean and Wind Energy,2015,2(4):213-222

10 ColluM,BorgM,ManuelL.Ontherelativeimportanceofloadsacting on a floatin vertical axis wind turbine system when evaluating the global system response//Proceedings of the ASME 2016 34th International Conference on Ocean,O ff shore and Arctic Engineering, OMAE2016-54628,Busan,South Korea,2016

11 Jonkman J,Buhl M.Loads analysis of a floatin o ff shore wind turbine using fully coupled simulation//Wind Power 2007 Conference &Exhibition,Los Angeles,USA,2007

12 Garrad Hassan GL.Bladed user manual version 4.2.Bristol,England:Garrad Hassan&Partners Ltd,St Vincent’s Works,2012

13 Myhr A,Maus KJ,Nygaard TA.Experimental and computational comparisons of the OC3-HYWIND and Tension-Leg-Buoy(TLB) floatin wind turbine conceptual designs//Proceedings of the 21st International O ff shore and Polar Engineering Conference,Maui,HI, USA,2011

14 Withee JE.Fully coupled dynamic analysis of a floatin wind turbine system.[Master Thesis].Massachusetts,USA:Massachusetts Institute of Technology,2004

15 Nielsen FG,Hanson TD,Kaare B.Integrated dynamic analysis of floatin o ff shore wind turbines//Proceedings of the International Conference O ff shore Mechanics and Arctic Engineering,OMAE 2006-92291,Hamburg,Germany,2006

16 Berg DE.An improved double-multiple stream tube model for the Darrieus type vertical-axis wind turbine//Proceedings of the sixth Biennial Wind Energy Conference and Workshop,Minneapolis, NM,USA,1983

17 Strickland JH,Webster BT,Nguyen TA.Vortex model of the Darrieus turbine:an analytical and experimental study.Sandia National Laboratories,Albuquerque,N.M.,USA,1980

18 Paraschivoiu I.Aerodynamic loads and performance of the Darrieus rotor.Journal of Energy,1982,6:406-412

19 Collu M,Borg M,Shires A,et al.Progress on the development of a coupled model of dynamics for floatin o ff shore vertical axis wind turbines//Proceedings of the ASME 2013 32nd International Conference on Ocean,O ff shore and Arctic Engineering,OMAE2013-54337,Nantes,France,2013

20 Wang K,Hansen MOL,Moan T.Dynamic analysis of a floatin vertical axis wind turbine under emergency shutdown using hydrodynamic brake.Energy Procedia,2014,53:53-69

21 Owens BC,Hurtado JE,Paquette JA.Aero-elastic modeling of large o ff shore vertical-axis wind turbines:development of the o ff shore wind energy simulation toolkit//Proceeding of the 54th AIAA/ASME/ASCE/A-HS/ASC Structures,Structural Dynamics, and Materials Conference,AIAA 2013-1552,Boston,MA.,USA, 2013

22 Liu LQ,Zhou B,Tang YG.Study on the nonlinear dynamical behaviour of deep sea Spar platform by numerical simulation and model experiment.Journal of Vibration&Control,2014,20(10): 1528-1553

23 Huang L,Liu LQ,Liu CY,et al.The nonlinear bifurcation and chaos of coupled heave and pitch motions of a truss spar platform.Journal of Ocean University of China,2015,14:795-802

24 Paraschivoiu I.Wind Turbine Design with Emphasis on Darrieus Concept.Canada:Polytechnic International Press,2002

25 IEC61400-3.Wind turbines,part 3:design requirements for o ffshore wind turbines.Geneva,Switzerland:International Electrochemical Commission,2009

26 Berg DE.An improved double-multiple stream tube model for the Darrieus type vertical-axis wind turbine//Proceedings of the sixth Biennial Wind Energy Conference and Workshop,Minneapolis, NM,USA,1983

27 Pan ZY,Vada T,Finne S,et al.Benchmark study of numerical approaches for wave-current interaction problem of o ff shore floater//Proceedings of the ASME 2016 34th International Conference on Ocean,O ff shore and Arctic Engineering,OMAE2016-54411,Busan,South Korea,2016

28 Faltinsen OM.Sea Loads on Ships and O ff shore Structures.Cambridge,UK:Cambridge University Press,1990

29 API 2A-WSD(RP 2A-WSD).Recommended practice for planning, designing and constructing fi ed o ff shore platforms-working stress design.WashingtonD.C.,USA:AmericanPetroleumInstitute,2000

30 Ractli ff e AT.Validity of quasi-static and approximate formulae in the context of cable and fl xible riser dynamics//Proceedings of the 4th International Conference on Behavior of O ff shore Structures, Delft,The Netherlands,1985

31 Paraschivoiu I.Double-multiple stream tube model for studying vertical-axis wind turbines.Journal of Propulsion,1988,4(4):370-377

32 Liu LQ,Zhang XR,Guo Y,et al.Study on the hydrodynamic characteristic of a spar type floatin foundation which used to support a vertical axis wind turbine//Proceedings of the ASME 2016 34th International Conference on Ocean,O ff shore and Arctic Engineering, OMAE2016-54337,Busan,South Korea,2016

33 Tang YG,Song K,Wang B.Experiment study of dynamics response for wind turbine system of floatin foundation.China Ocean Eng, 2015,29(6):835-846

DYNAMIC MODELING,SIMULATION AND MODEL TESTS RESEARCH ON THE FLOATING VAWT1)

Liu Liqin2)Guo Ying Zhao Haixiang Tang Yougang
(State Key Laboratory of Hydraulic Engineering Simulation and Safety of Tianjin University，Tianjin300072，China)

This paper presented motion responses of the floatin VAWT(vertical axis wind turbine)considering the coupling between aerodynamics and hydrodynamics,the method of aerodynamics of fi ed VAWT was improved to calculate the aerodynamics of the floatin VAWT.The equations of surge,heave and pitch motions of the floatin VAWT were established considering the damping forces,wave forces,wind loads,mooring forces,and so on.The formula of wind loads acting on the blades were deduced by the double-multiple-stream tube theory considering the dynamic stall and motions of the floatin foundation,and a computing code was developed.Taking the Sandia 17m wind turbine as an example,the validity of the aerodynamics computing code was verified The model tests were carried out,where the wind turbine is Φ-Darrieus type and the foundation is truss Spar type.The results obtained by the model tests were compared with those obtained by the numerical simulation,and the coupling computing code was verified.I is found that,the RAO(response amplitude operator)curves of heave and pitch motions of the floatin VAWT obtained by numerical calculation agree well with those obtained by model tests,and the validation of the coupling computing code was verified However,there is di ff erence between the results of numerical calculation and the model tests.This is because the di ff erences betweenthe numerical model and the model tests,mainly regarding the degrees of freedom of the floatin VAWT motions,the damping,and the wind forces.

floatin VAWT,coupling between aerodynamics and hydrodynamics,numerical simulation,model tests

P75,TK81

A

10.6052/0459-1879-16-264

2016–09–20收稿，2016–12–15錄用,2016–12–15網絡版發表.

1)國家自然科學基金(51579176)、上海交通大學海洋工程重點試驗室開放基金(1501)和天津市自然科學基金(16JCYBJC21200)資助項目.

2)劉利琴，副教授，主要研究方向：船舶與海洋工程動力學，海洋可再生能源.E-mail：liuliqin@tju.edu.cn

劉利琴,郭穎,趙海祥,唐友剛.浮式垂直軸風機的動力學建模、仿真與實驗研究.力學學報,2017,49(2):299-307

Liu Liqin,Guo Ying,Zhao Haixiang,Tang Yougang.Dynamic modeling,simulation and model tests research on the floatin VAWT.Chinese Journal of Theoretical and Applied Mechanics,2017,49(2):299-307