含概率與區間混合不確定性的系統可靠性分析方法1)

劉海波 姜 潮鄭 靜 韋新鵬 黃志亮

(湖南大學機械與運載工程學院，特種裝備先進設計技術與仿真教育部重點實驗室，長沙410082)

含概率與區間混合不確定性的系統可靠性分析方法1)

劉海波 姜 潮2)鄭 靜 韋新鵬 黃志亮

(湖南大學機械與運載工程學院，特種裝備先進設計技術與仿真教育部重點實驗室，長沙410082)

系統可靠性問題中通常存在大量的不確定參數，傳統方法一般是基于概率模型對系統進行可靠性分析，但是實際工程中由于數據缺乏或試驗條件的限制往往難以得到參數的精確概率分布.本文將結構體系一部分樣本信息充足的不確定變量用隨機變量進行描述，而另一部分樣本缺乏的用區間表示，并提出了一種新的含概率與區間混合不確定性的系統可靠性分析方法.首先，基于一個高效求解方法獲得單失效模式下結構的最小可靠度指標；再針對多失效模式下含概率與區間混合不確定性問題建立了系統可靠性分析模型；考慮各失效模式之間的相關性，通過線性相關度計算方法求得相關系數矩陣；最后提出了串聯體系和并聯體系可靠度求解方法.3個數值算例表明，該方法可以實現含概率與區間混合的多個非線性失效模式下系統可靠度的計算.通過對比傳統的概率可靠性分析方法，本文方法只需要少量的不確定信息便可確保系統更加安全，更適合復雜結構系統可靠性的分析和設計.

系統可靠性,概率與區間混合不確定性,最大失效概率,失效模式相關性

引言

工程實際中經常存在著與材料特性，邊界條件和載荷等有關的各種不確定性[1]，概率模型是目前工程中處理不確定性的最重要方法.基于傳統概率模型的可靠性分析方法應用廣泛，其中包括一次二階矩[2-5]，二次二階矩[6-7]，蒙特卡洛仿真[8]，基于可靠性的優化設計[9-10]等.但概率模型對測試數據的強依賴性和實際工程中可得數據的缺乏，又在一定程度上限制了它在實際工程中的應用，近年來發展出的非概率的區間分析方法，可一定程度上解決概率方法對大樣本量的依賴性問題，得到工程人員的關注.Ben-Haim等[11-13]認為當掌握的數據信息較少而不足以精確定義概率模型時，宜采用區間集合模型描述不確定性.Rao等[14]基于輸入不確定參數的區間度量，通過求解區間線性方程組對不確定結構進行了分析.Qiu和Elishako ff[15]基于區間模型，采用區間算法和擾動技術成功地對桁架結構進行了結構優化.郭書祥等[16]通過對不確定參數的區間描述，提出了一種非概率可靠性的度量體系及分析方法.王曉軍等[17]基于不確定性的區間集合模型描述,研究了非概率集合模型的結構可靠性分析.

在實際問題中，結構的某些不確定性參數在實踐中已累積有大量的樣本，但另外一些不確定性參數由于測試難、成本高等問題只能獲得少量的樣本.對于該類問題，采用單一的概率或者區間不確定模型則難以對問題進行有效分析.因此，研究概率與區間混合不確定性模型及其可靠性分析具有重要的工程意義.對于概率與區間混合不確定性模型的研究目前國際上已有一些工作出現.E1ishako ff等[18]研究了概率模型和凸模型的混合不確定性問題.郭書祥等[19]結合概率和非概率模型,通過兩級功能方程的逐次建立,給出結構可靠性的概率度量.尼早等[20]建立了概率--模糊--區間的混合可靠性模型，定義了結構的混合可靠度.Du等[21]在概率變量和區間變量并存的條件下,提出了一種基于可靠性的優化方法，隨后Du[22]又針對雙層嵌套優化問題，構造了一種概率區間高效可靠性分析方法.程遠勝等[23]提出了結構穩健設計的混合可靠性模型.Luo等[24]通過定義一個最小嵌套優化問題得到的可靠性指標來度量結構的安全性.Kang等[25]通過對不確定參數的概率和凸集混合建模，提出了一種基于可靠性的結構優化設計技術.Jiang等[26-29]通過結合概率模型和非概率區間模型，提出了多種高效的混合可靠性分析方法.盡管目前已有一系列概率與區間混合模型及可靠性分析方法被提出來，但是這些方法大都是針對單一失效模式問題.但是一般情況下，結構的失效模式并不止一個，即存在系統可靠性問題[30].體系可靠度作為工程結構整體安全性的重要度量，是結構可靠性研究領域的重點和難點.對于存在概率與區間混合不確定性的結構系統可靠性分析目前已經引起了國內外學者的關注.Adduri等[31]基于近似的聯合功能函數，提出了存在區間變量的結構系統可靠度界限的分析方法.Qiu等[32]結合經典概率理論和區間算法，研究了概率區間結構系統可靠性問題.Wang等[33]基于區間可靠性模型和概率運算，提出了概率區間混合系統可靠性分析方法.盡管目前已有一些概率與區間混合系統可靠性求解方法，這些方法大多是針對簡單的線性失效模式問題的.但在實際工程問題中，失效模式通常是非線性的，甚至很多時候都是通過有限元(FEM)等數值分析方法獲得，故針對實際工程問題發展和建立能處理非線性失效模式的概率與區間系統可靠性分析方法具有較為重要的工程意義.

本文針對概率與區間混合不確定性問題，構建了一種系統可靠性分析方法，可以實現多個非線性失效模式下結構可靠度區間的計算.首先基于一個高效求解方法獲得單失效模式下結構的可靠度指標；再針對多失效模式下含概率與區間混合不確定性問題建立了系統可靠性分析模型；考慮各失效模式之間的相關性，通過線性相關度計算方法求得失效模式間的相關系數矩陣；最后提出了串聯和并聯體系可靠度求解方法，并由多維高斯分布函數獲得結構體系的最大失效概率.

1 單失效模式下的概率與區間混合可靠性分析

如果結構中既存在概率變量又存在區間變量，則結構功能函數可表示為

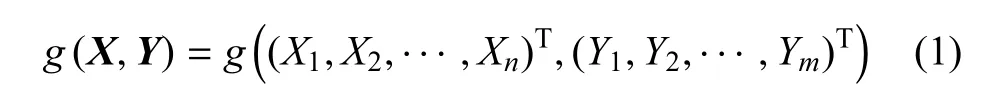
式中X=(X1,X2,···,Xn)T為n個獨立概率變量組成的隨機向量；Y=(Y1,Y2,···,Ym)T為m個獨立區間變量組成的區間向量.如使用一次二階矩[2-4]進行分析，首先要將隨機向量X標準化，即X通過概率變換轉化為標準正態向量U

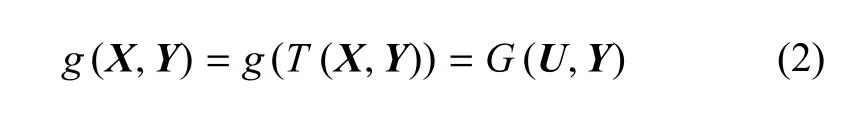
式中T為概率轉換函數.在混合模型中，由于存在區間變量，原空間中的極限狀態方程映射到標準正態空間后構成的極限狀態曲面不再是單一的曲面，而是由兩個邊界面和構成的極限狀態帶[22]，如圖1所示.

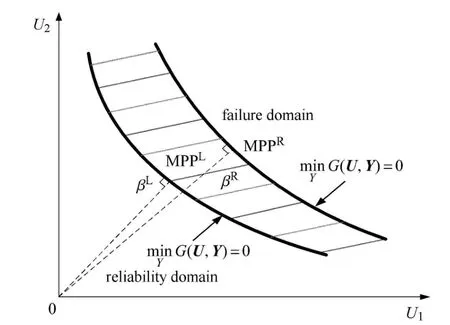
圖1 極限狀態曲面邊界Fig.1 The bound of limit-state surfaces

因此，曲面帶區域的兩條邊界對應的可靠度指標β不再是確定值，而是一波動區間

式中βL與βR分別表示可靠度指標的最小值與最大值.基于一次二階矩方法，可構造如下兩個優化問題[21-22]，得到上述極限狀態帶的可靠度指標區間

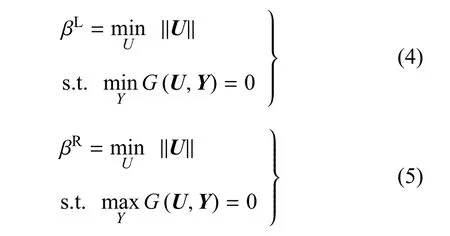
式(4)和式(5)為雙層嵌套優化問題，為提高計算效率，可采用文獻[21-22]提出的解耦方法，將區間分析嵌入到最可能失效點的尋找過程中，每次迭代過程中依次進行概率分析和區間分析，經過多次迭代最終使內、外層同時達到穩定解.

下面以求解βL為例，給出具體的計算流程.假設在第k步迭代過程中得到Uk和Yk，在下一步迭代過程中，先固定區間向量Yk，再利用改進的HL-RF迭代法，即iHL-RF[34-35]求得Uk+1

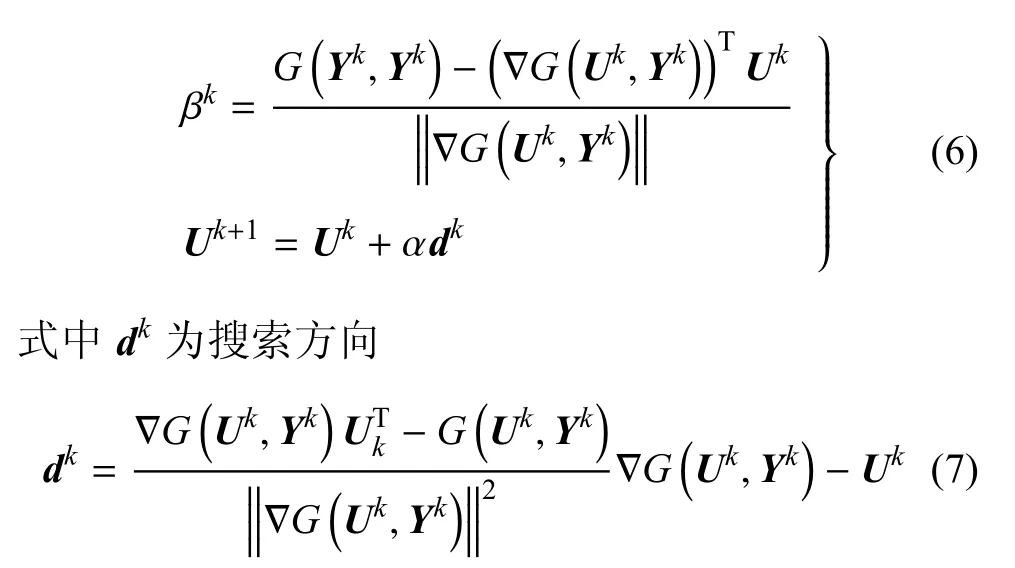
獲得Uk+1后，再通過求解以下優化問題得到Yk+1

2 多失效模式下的概率與區間混合可靠性分析

第1節中的結構可靠度計算方法，是針對單一失效模式而言的，即功能函數只有一個.但是很多情況下，結構的失效模式并不止一個，如壓力容器的失效，可能同時存在屈服、疲勞和斷裂等失效模式；各失效模式的功能函數由于有相同的載荷和幾何參數等，導致結構各失效模式間具有相關性[30].一般情況下，結構體系可靠性模型根據拓撲結構可分為三類[31]：串聯體系、并聯體系和混聯體系模型，如圖2所示.

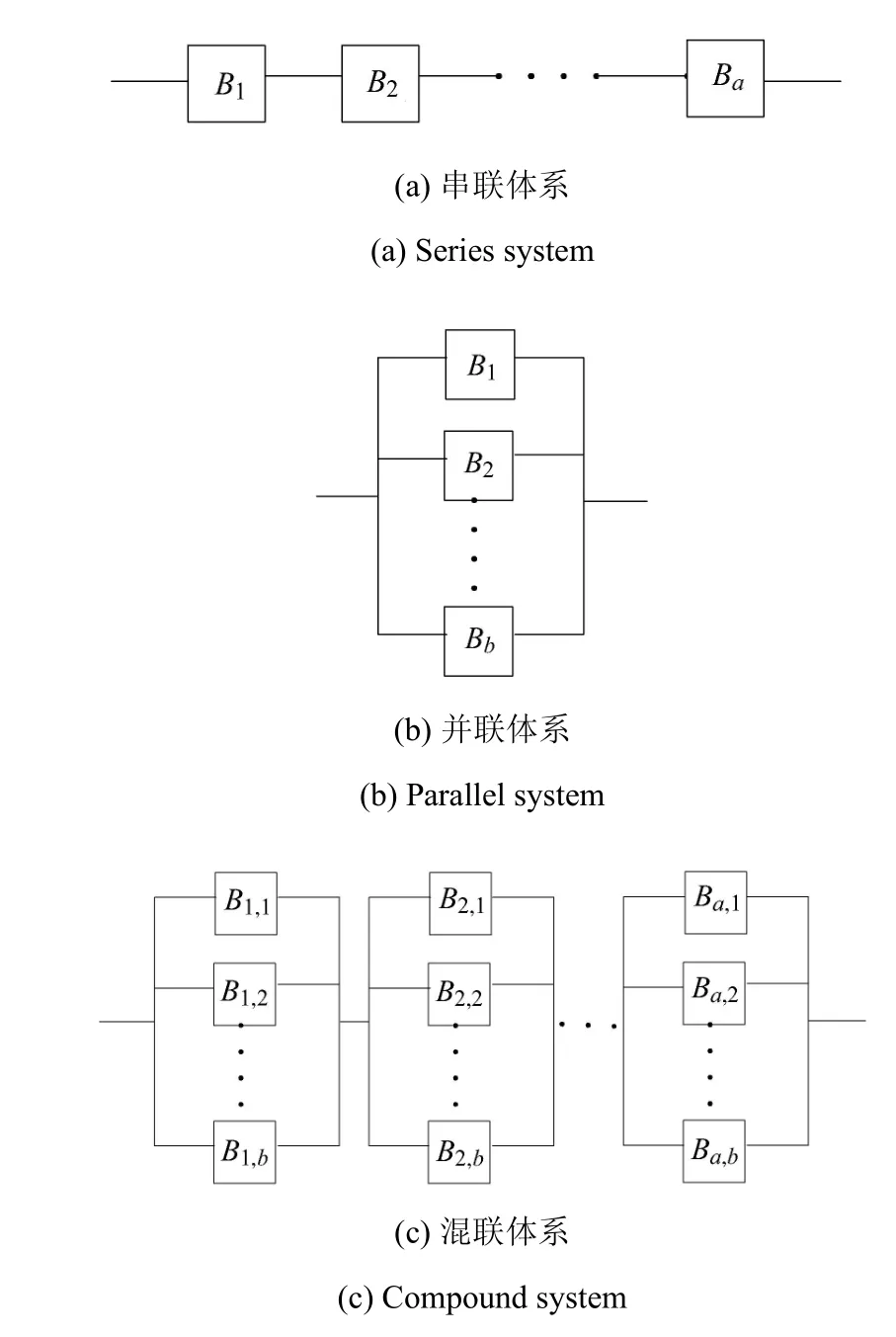
圖2 3類體系可靠性模型Fig.2 Three kinds of system reliability models

為后續推導方便，圖2所示的串聯體系、并聯體系和混聯體系的失效概率可統一記為

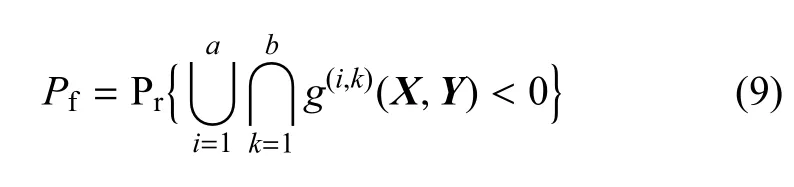
式中,Pr{}代表概率,a和b分別為串聯單元數目和并聯單元數目，當a=b=1時，式(9)表示單失效模式失效概率；當b=1,a＞1時，式(9)表示圖2(a)串聯體系失效概率；當a=1,b＞1時，式(9)表示圖2(b)并聯體系失效概率；當a＞1,b＞1時，式(9)表示混聯體系失效概率.串聯體系和并聯體系可以被用來建立任何體系的兩個基本體系，如實際的超靜定結構通常有多個失效模式，每個失效模式可簡化成一個并聯體系，而多個失效模式又可簡化成串聯體系，這就構成了混聯結構體系.因此在混聯體系中，一般可將一個并聯體系直接作為一個失效模式看待，每一個失效模式都可從力學上建立與其對應的功能函數，從而可將并聯--串聯體系簡化為串聯體系計算[36]，這里不再具體闡述.

計算系統失效概率的主要困難在于需要考慮概率變量和區間變量各失效模式之間的相關性.下面，首先進行多失效模式的相關性分析，再具體對串聯體系和并聯體系失效概率進行求解.

2.1 多失效模式間的相關性分析

設存在概率與區間混合不確定性的結構或系統有K個失效模式，每一個失效模式對應一個功能函數

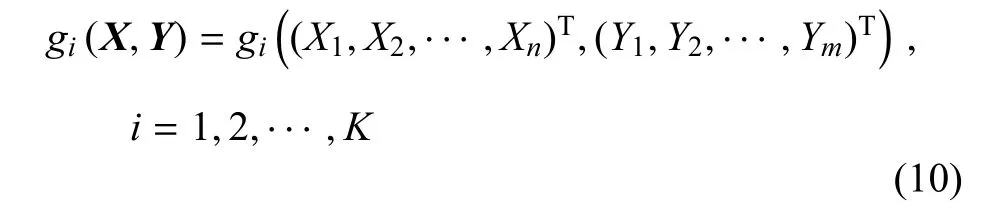
結合式(2)，將式(10)進行概率變換

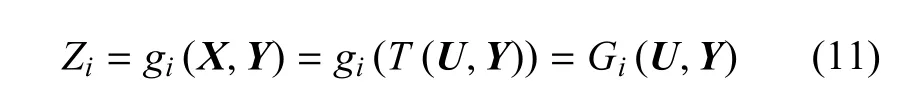
為處理功能函數的相關性，可在功能函數Zi的設計驗算點(U?,Y?)處固定區間變量Y?，將式(11)對隨機變量U展開成一階Taylor級數

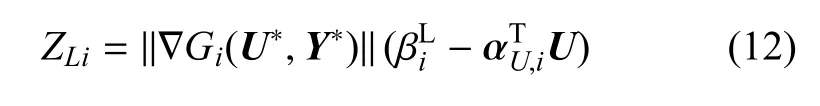
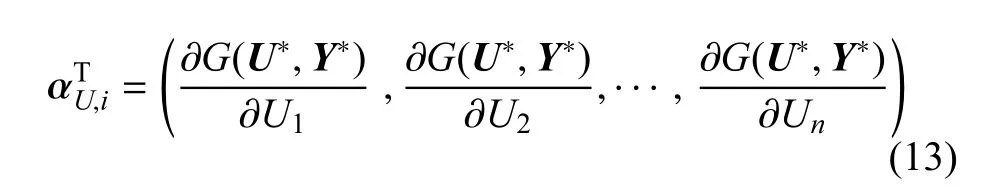
由式(13)可近似求得第i個失效模式和第j個失效模式功能函數間的相關系數[36]

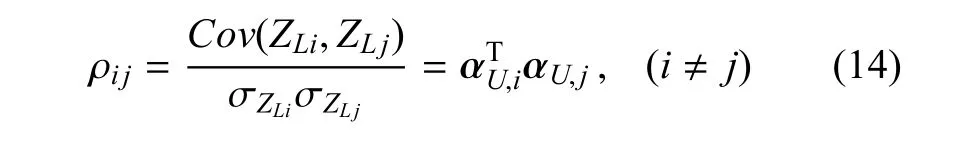
2.2 串聯系統可靠性求解

考慮具有a個失效模式的串聯體系.由于存在區間變量，原空間中的極限狀態方程映射到標準正態空間后構成的極限狀態面不再是唯一曲面而是一個曲面“帶”，如圖3(a)所示.

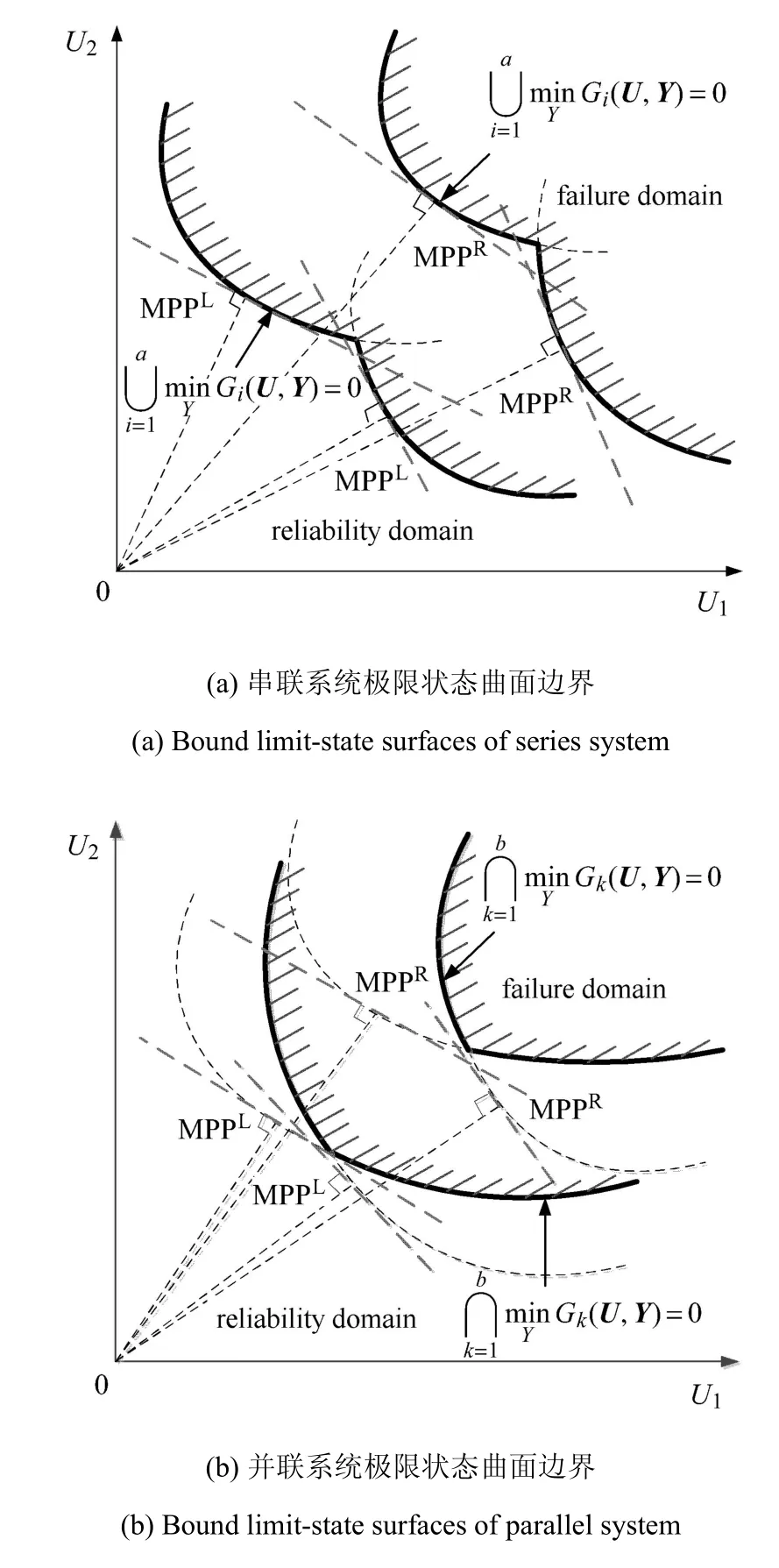
圖3 系統極限狀態曲面邊界Fig.3 Bound limit-state surfaces of structural system

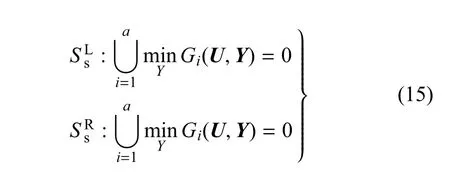
因而串聯系統失效概率Pf為一區間，其邊界如下

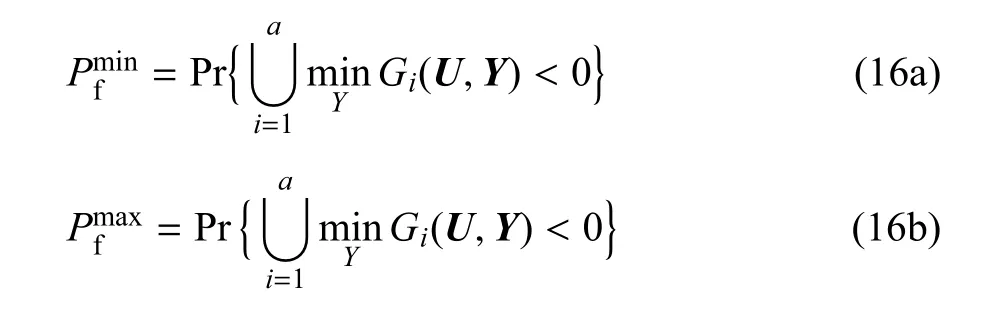
對串聯體系進行可靠性分析，并計算串聯體系最大失效概率，可將式(16b)變為

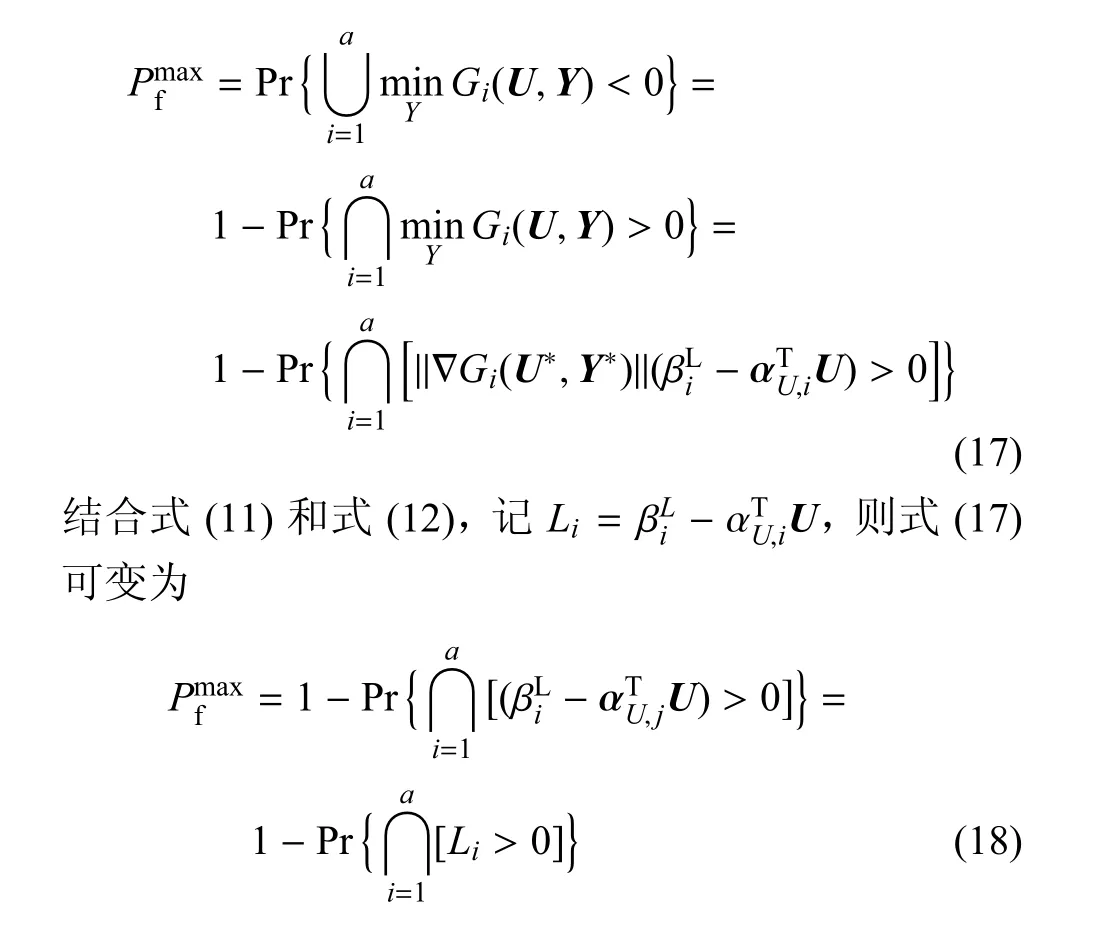
根據串聯體系最大失效概率計算方法[37]，式(18)可變為

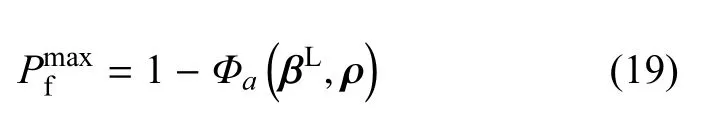
其中Φa(·)為a維標準高斯分布函數，為功能函數G(U,Y),i=1,2,···,a對應的最小可靠度指標組成的向量. ρ為Gi(U,Y),i=1,2,···,a的相關系數矩陣，通過式(14)便可得到式(19)中ρ的每一個元素.通過式(19)中的多維高斯分布函數可計算出串聯系統最大失效概率.多維高斯分布函數的計算可參考文獻[38-42]，在商業軟件Matlab中也有相應的庫函數.

2.3 并聯系統可靠性求解

考慮具有b個失效模式的并聯體系.由于存在區間變量，原空間中的極限狀態方程映射到標準正態空間后構成的極限狀態面如圖3(b)所示，則并聯系統極限狀態帶的下邊界和上邊界可表示為

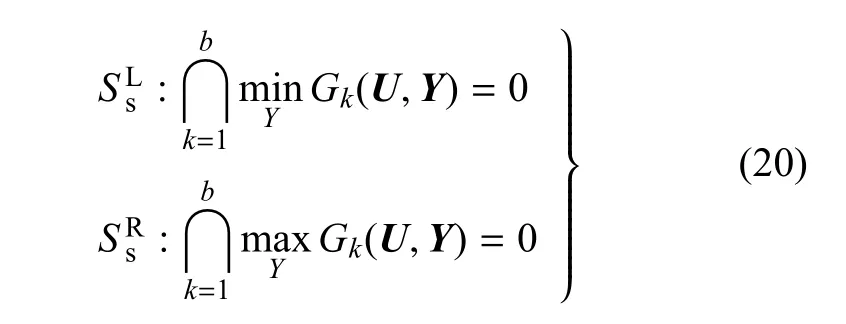
因而并聯系統失效概率Pf也為一個區間，其邊界如下

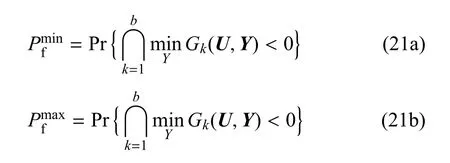
對并聯體系進行可靠性分析，并計算并聯體系最大失效概率，將式(21b)變為

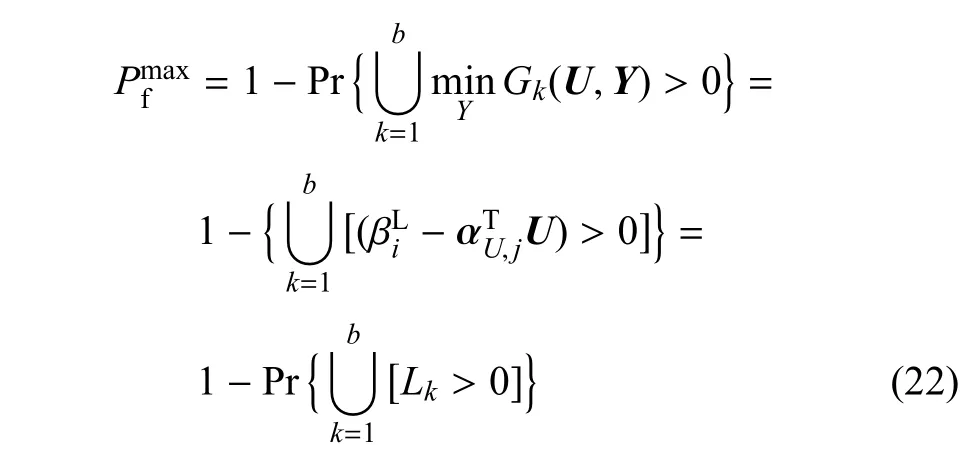
記上式中的Lk＞0為事件Dk，則式(22)可變為

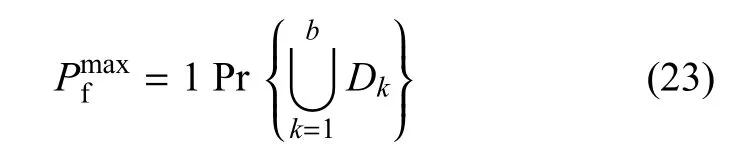
根據并聯事件概率計算公式[43]，將式(23)變為

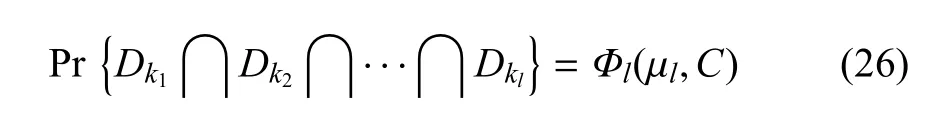
其中Φl(·)為l維高斯累積分布函數.利用式(26)可計算出式(24)等號右邊的所有概率項，最終可獲得并聯結構體系最大失效概率

3 數值算例

本節將本文方法應用于3個數值算例.第1個為具有雙失效模式的并聯體系算例，第2為具有雙失效模式的串聯體系算例，第3個為實際工程應用算例.由于本文得到的是系統失效概率的區間界限，因此本節從可靠性分析與設計的角度對比傳統概率可靠性[36]方法，進一步說明概率與區間混合可靠性分析方法的適用性.

3.1 兩單元Daniels系統算例

如圖4所示為一并聯的兩單元Daniels系統，該算例在文獻[44]的基礎上改進而來.單元1的截面長寬分別為c1和d1，單元2的截面長寬分別為c2和d2，P為系統所受載荷，當兩單元均屈服的時候，結構失效.兩單元對應的功能函數分別表示為

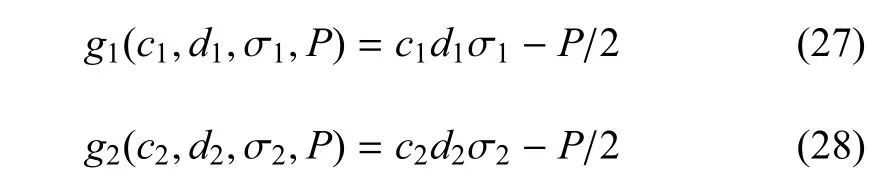
其中σ1和σ2分別為單元1和單元2的屈服強度.式(27)和式(28)中的概率和區間變量參數如表1所示.表中，對于概率變量，參數1和參數2分別表示均值和標準差；對于區間變量，參數1和參數2分別表示下邊界和上邊界.

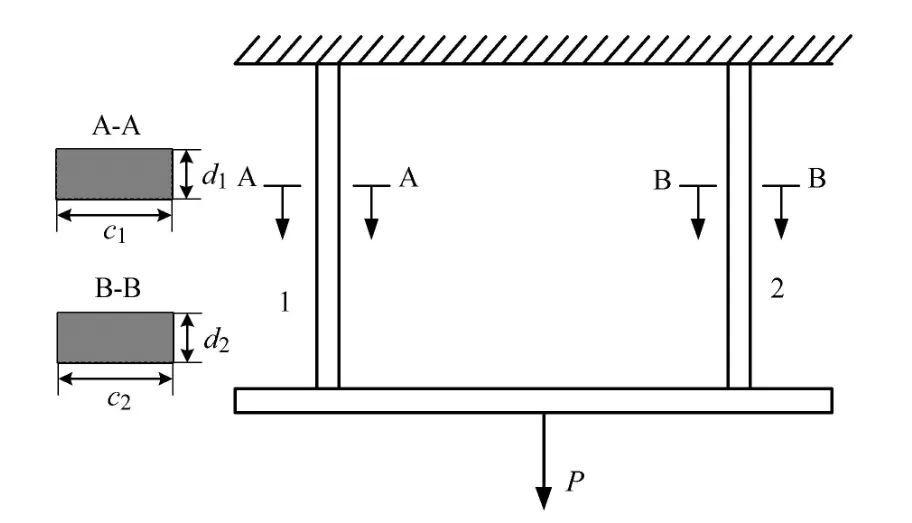
圖4 兩單元Daniels系統[44]Fig.4 A two-component Daniels system[44]

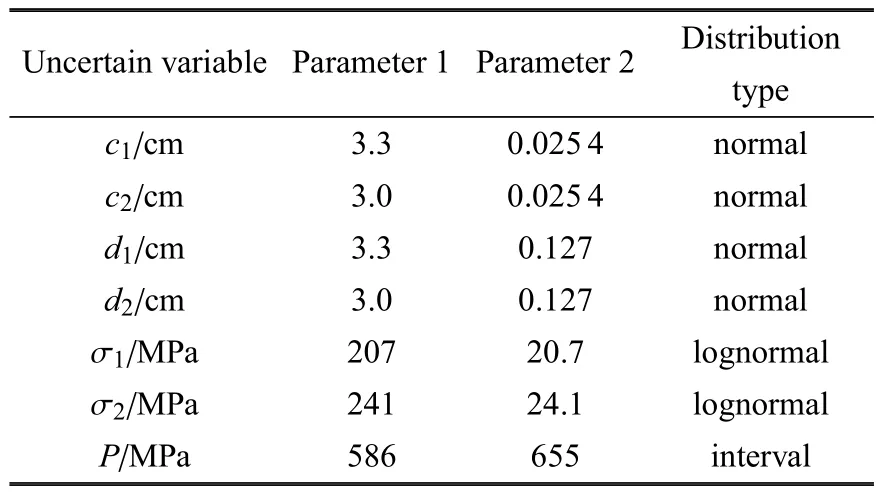
表1 兩單元Daniels系統不確定變量分布類型和參數Table 1 Distribution types and parameter of uncertain variables of the two-component Daniels system

考慮兩單元 Daniels并聯系統，對該問題進行可靠性分析，計算所得結果如表2所示.為說明本文方法的有效性，這里亦給出了將區間變量P假設為均勻分布的傳統概率可靠性方法的計算結果；由表2可知，本文方法獲得的兩單元Daniels系統并聯體系最小可靠度指標 βL=1.391和最大失效概率為而傳統的概率可靠性方法計算的并聯系統可靠度指標β=1.809和失效概率為Pf=0.0352；可看出基于概率可靠性方法得到的系統失效概率小于本文方法計算的最大失效概率，這會導致較大的分析誤差，并會對結構體系的分析和設計帶來一定的風險，而本文方法計算的結果可確保結構體系更加的安全.另外，通過對比蒙特卡羅計算結果，說明本文方法不僅能保證精度，還提高了計算效率.

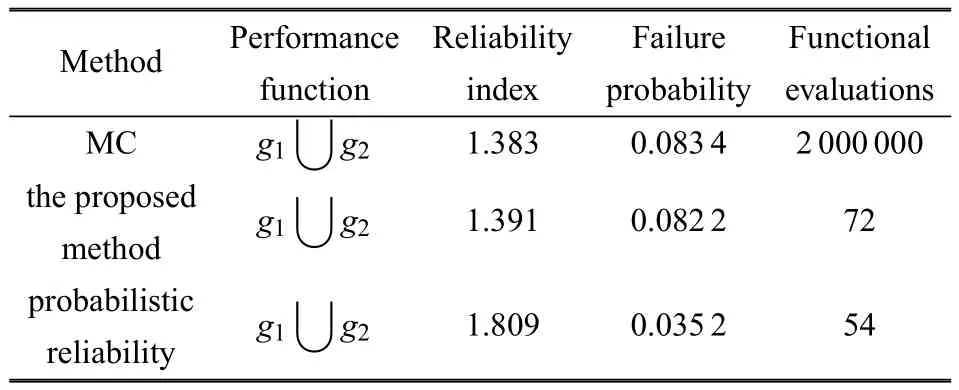
表2 兩單元Daniels系統的可靠性分析結果Table 2 The reliability analysis results of the two-component Daniels system

3.2 懸壁梁算例

如圖5所示的懸臂梁，該算例在文獻[21]的基礎上改進而來.懸臂梁長度為L，橫截面寬度為t，高度為h，懸臂梁的頂端承受水平和垂直作用力分別為Px和Py.懸臂梁固定端處最大應力不能超過屈服強度極限值S=370MPa，懸臂端處最大許用位移D0=25mm，懸臂梁彈性模量E=210GPa；考慮位移失效模式和應力失效模式，功能函數可以分別表示為

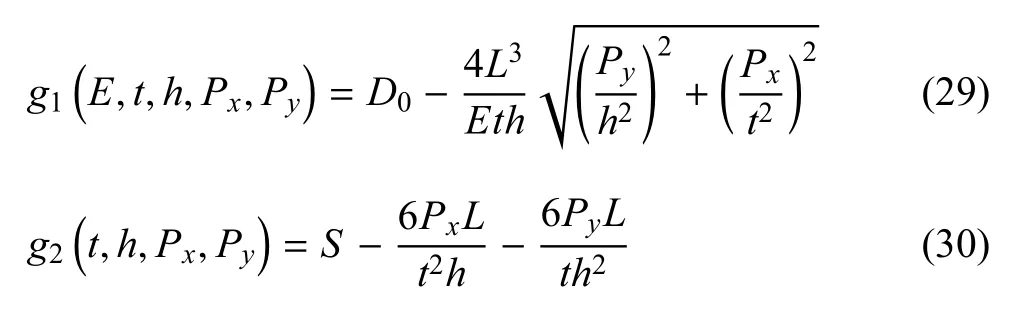
將t,h和L處理成概率變量，Px和Py處理成區間變量，其分布類型和分布參數見表3.參數1和參數2的含義與表1相同.

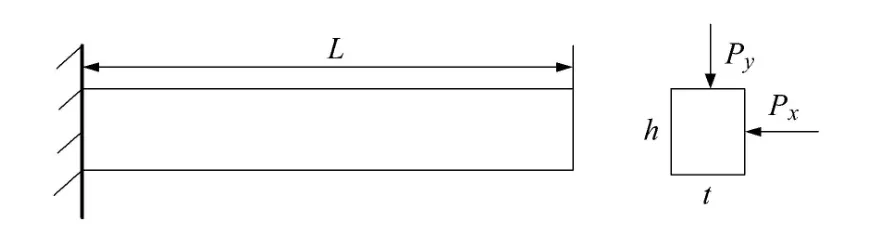
圖5 懸臂梁[21]Fig.5 A cantilever beam[21]

表3 懸臂梁的不確定變量分布類型和參數Table 3 Distribution types and parameter of uncertain variables of the cantilever beam

考慮懸臂梁的雙失效模式串聯體系，對該問題進行可靠性分析，計算所得結果如表4所示.為說明本文方法的有效性，這里仍然給出了將區間變量Px和Py假設為均勻分布的傳統概率可靠性方法的計算結果；由表4可知，本文方法獲得的懸臂梁雙失效模式串聯體系的最小可靠度指標βL=1.853和最大失效概率為而傳統的概率可靠性方法計算的串聯系統可靠度指標β=2.617和失效概率為Pf=0.0044；同樣可看出基于概率可靠性方法得到的串聯系統失效概率小于本文方法計算的最大失效概率，這會導致較大的分析誤差，而本文方法計算的結果比概率可靠性方法更加精確，可確保結構系統更加安全.

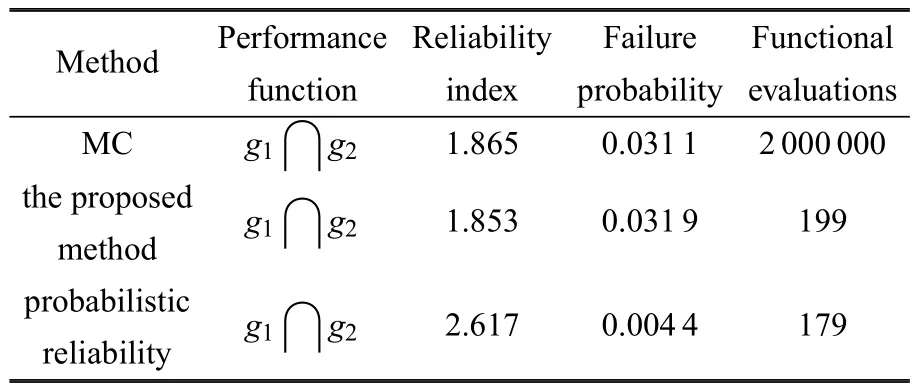
表4 懸臂梁的系統可靠性分析結果Table 4 The system reliability analysis results of the cantilever beam

3.3 車輛耐撞性分析

考慮一個在文獻[45]基礎上修改得到的車輛耐撞性問題，該算例結合車輛高速和低速耐撞性的特點，綜合考慮相關部件，進行整車體系可靠性分析.如圖6所示，以兩種情況下的車輛耐撞性作為可靠性分析對象，其中包括15km/h低速偏置碰撞和56km/h的高速正面碰撞.低速碰撞時，因為乘員安全沒有受到威脅，所以要求保護車輛主體；即前縱梁變形應盡可能減小，以降低車輛碰撞損傷修復所需要的費用.由此，低速碰撞中前縱梁內、外板吸收總能量E應小于額定值E0=500J.高速碰撞時，主要考慮乘員的安全，要求最大程度減小乘員的傷害并保證乘員的安全空間.選取發動機上下兩個標記點的侵入量IH和IL作為衡量車身安全性的指標，分別應小于給定的額定值變量X1～X3分別表示前保險杠厚度和吸能盒內、外板厚度；變量Y1,Y2分別表示前縱梁內、外板厚度，變量X1～X3均為正態隨機變量，Y1,Y2因試驗樣本缺乏，僅能給定區間，不確定變量具體信息如表5所列.表中，參數1和2的含義與表1相同.對于低速碰撞和高速碰撞兩種情況分別建立數值仿真模型，2個模型采用同一車輛的有限元模型而僅對碰撞壁障做出相應修改：如圖7所示，該車輛有限元模型中含有755個部件，998220個節點，977742個單元.為提升計算效率，對2個仿真模型分別采樣65次，并逐一構建功能函數的二階響應面，如表6所列.

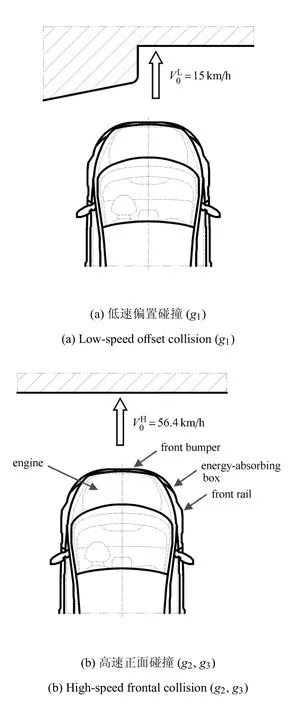
圖6 汽車耐撞問題試驗[45]Fig.6 The experiment of the vehicle crashworthiness problem[45]

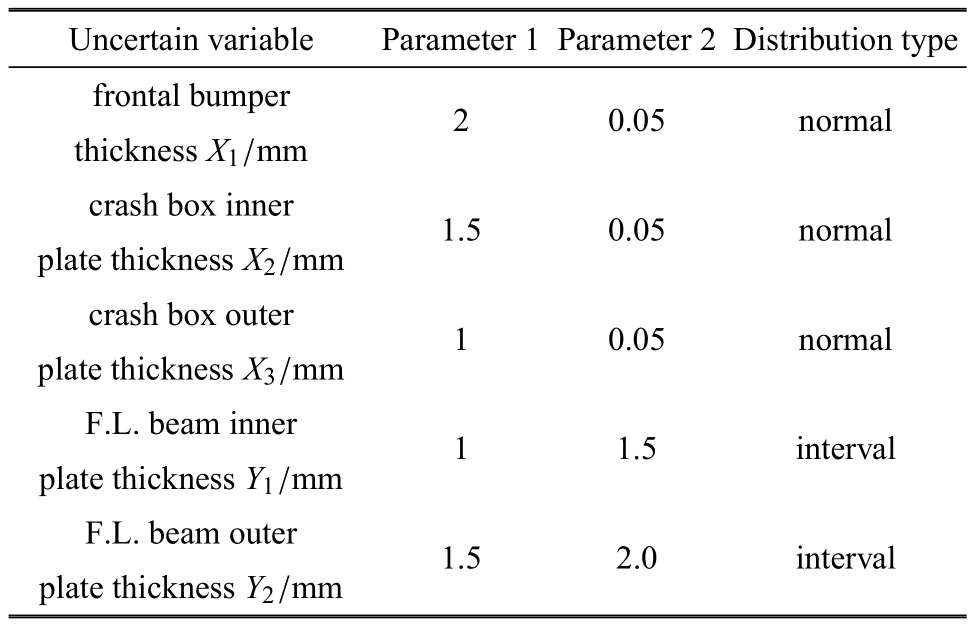
表5 車輛耐撞問題的不確定變量分布類型和參數Table 5 Distribution types and parameter of uncertain variables of the vehicle crashworthiness problem

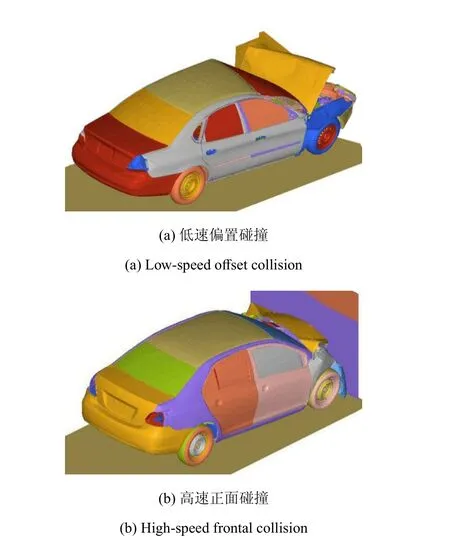
圖7 碰撞試驗的有限元模型[45]Fig.7 FEMs for the vehicle crashworthiness problem[45]

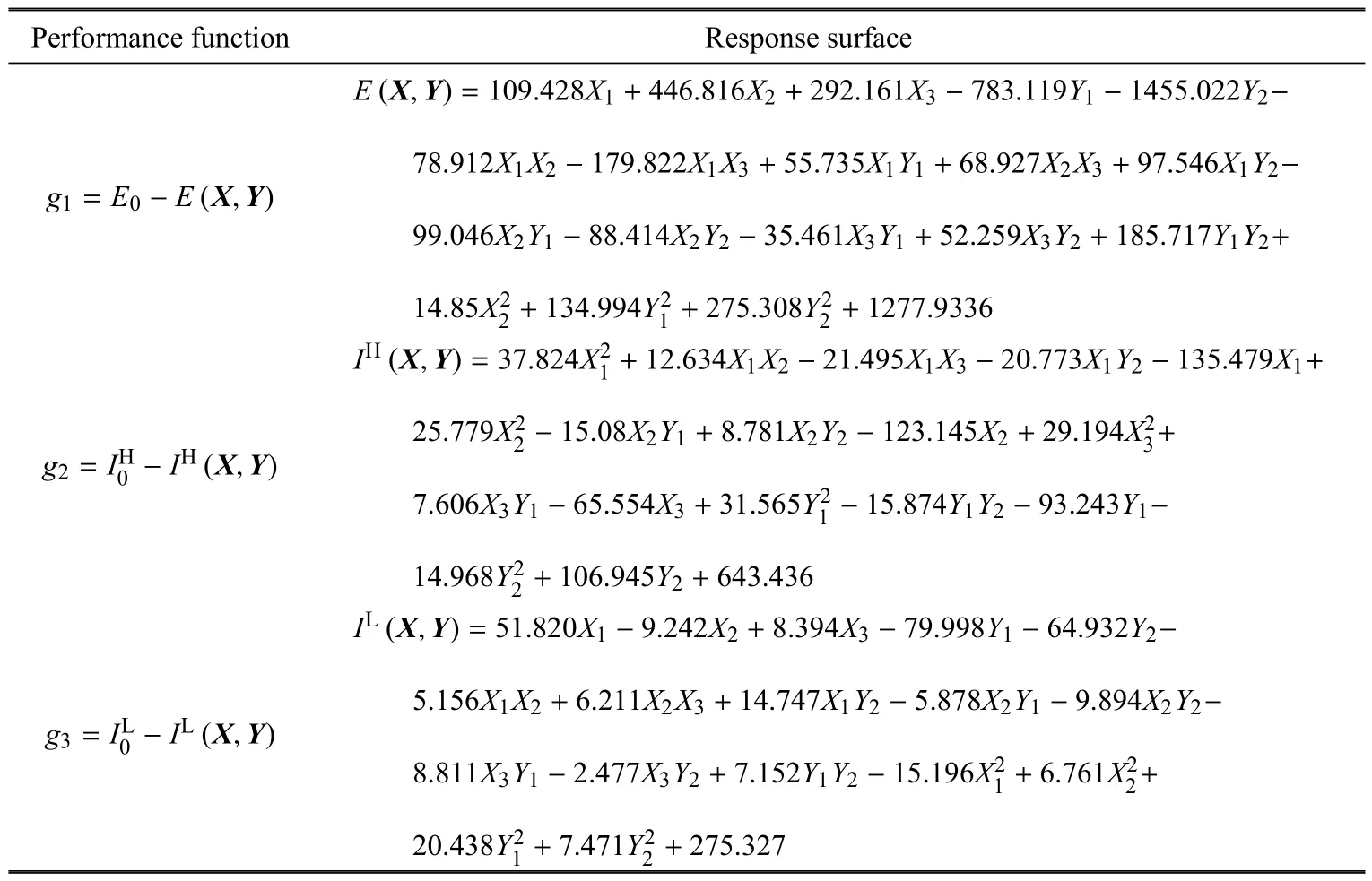
表6 車輛耐撞問題的3個功能函數響應面Table 6 Response surface for the three performance functions in the vehicle crashworthiness problem

考慮低速偏置碰撞和高速正面碰撞的3個失效模式串聯體系的車輛耐撞性問題，對該問題進行可靠性分析，計算所得結果如表7所示.為說明本文方法的有效性，這里仍然給出了將區間變量Y1和Y2假設為均勻分布的傳統概率可靠性方法的計算結果；由表4可知，本文方法獲得車輛耐撞的3個失效模式串聯體系的最小可靠度指標 βL=1.364和最大失效概率為而傳統的概率可靠性方法計算的可靠度指標β=2.202和失效概率為Pf=0.0138；可看出本文方法計算的系統最大失效概率將近為概率可靠性方法結果的8倍，說明基于概率可靠性方法得到的串聯系統失效概率小于實際的最大失效概率，這會導致較大的分析誤差，而本文方法計算的結果比概率可靠性方法更加的精確.

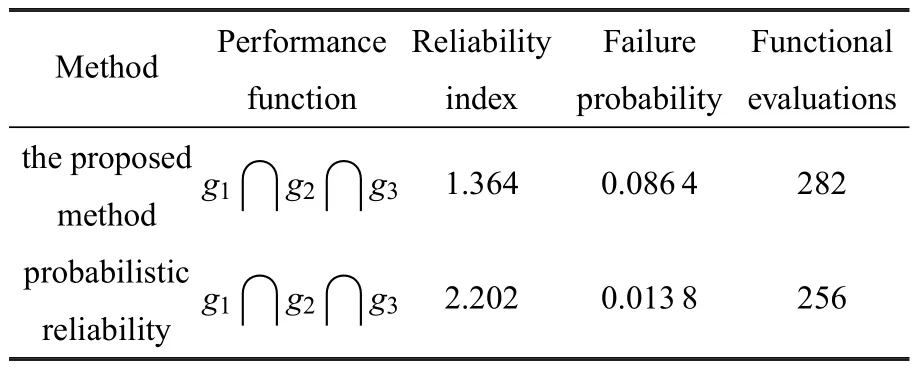
表7 車輛耐撞問題的系統可靠性分析結果Table 7 The system reliability analysis results of the vehicle crashworthiness problem

4 結論

本文針對既存在概率變量又存在區間變量的結構體系問題，提出了一種新的可靠性分析方法.首先，基于一個高效求解方法獲得單失效模式下結構的最小可靠度指標；再給出了含概率與區間混合不確定性的系統模型；考慮系統各失效模式之間的相關性，通過在設計驗算點處固定區間變量并結合線性相關度計算方法求得這些功能函數的相關系數矩陣；最后提出了串聯體系和并聯體系可靠度求解方法，并通過計算多維高斯分布函數獲得結構體系的最大失效概率.從可靠性分析與設計的角度對比傳統概率可靠性方法，3個數值算例表明本文方法計算的結果比概率可靠性方法要更精確，可確保結構系統更加的安全；可見對于存在樣本信息缺乏的結構體系，考慮含概率與區間混合不確定性的系統模型更適合體系可靠性的分析與設計.

1 Guo J,Du XP.Sensitivity analysis with mixture of epistemic and aleatory uncertainties.AIAA J,2007,45:2337-2349

2 Hasofer AM,Lind NC.Exact and invariant second-moment code format.ASME J Eng Mech Div,1974,100:111-121

3 Rackwitz R,Fiessler B.Structural reliability under combined random load sequences.Comput Struct,1978,9:489-494

4 Fiessler B,Rackwiyz R,Neumann H.Quadratic limit states in structural reliability.Journal of the Engineering Mechanics Division,1979,105(4):661-676

5 Hohenbichler M,Rackwitz R.Non-normal dependent vectors in structural safety.ASME J Eng Mech Div,1981,107(6):1227-1238

6 Breitung KW.Asymptotic approximation for multinormal integrals.ASCE J Eng Mech,1984,110(3):357-366

7 Breitung KW.Asymptotic Approximation for Probability Integrals. Berlin:Springer-Verlag,1994

8 Rubinstein RY,Kroese DP.Simulationand the Monte-Carlo method. 2nd ed.New York:Wiley,2007

9 Du XP,Chen W.Sequential optimization and reliability assessment method for efficient probabilistic design.Journal of Mechanical Design,2004,126(2):225-233

10 Liang JH,Mourelatos ZP,Nikolaidis E.A single-loop approach for system reliability-based design optimization.Journal of Mechanical Design,2007,129:1215-1224

11 Ben-Haim Y,Elishako ffI.Convex Models of Uncertainty in Applied Mechanics.Amsterdam:Elsevier Science,1990

12 Ben-Haim Y.A non-probabilistic concept of reliability.Structural Safety,1994,14:227-245

13 Ben-Haim Y.Robust Reliability in the Mechanical Sciences.Berlin: Springer-Verlag,1996

14 Rao SS,Berke L.Pantelides C.Analysis of uncertain structural systems using interval analysis.AIAA Journal,1997,35(4):727-735

15 Qiu Z,Elishako ffI.Antioptimization of structures with large uncertain-but-non-random parameters via interval analysis.Computer Methods in Applied Mechanics and Engineering,1998, 152(3):361-372

16 郭書祥,呂震宙,馮元生.基于區間分析的結構非概率可靠性模型.計算力學學報,2001,18(1):56-60(Guo Shuxiang,Lu Zhenzhou,Feng Yuansheng.A non-probabilistic model of structural reliabilitybasedonintervalanalysis.ChinJComputMech,2001,18(1): 56-60(in Chinese))

17 王曉軍,邱志平,武哲.結構非概率集合可靠性模型.力學學報, 2007,39(5):641-646(Wang Xiaojun,Qiu Zhiping,Wu Zhe.Nonprobabilistic set-based model for structural reliability.Chin J Theor App Mech,2007,39(5):641-646(in Chinese))

18 Elishako ffI,Colombi P.Combination of probabilistic and convex models of uncertainty when scare knowledge is present on acoustic excitation parameters.Comput Meth Appl Mech Eng,1993,104: 187-209

19 郭書祥,呂震宙.結構可靠性分析的概率和非概率混合模型.機械強度,2002,24:524-526(Guo Shuxiang,Lu Zhenzhou.Hybrid probabilistic and non-probabilistic model of structural reliability.J Mech Strength,2002,24:524-526(in Chinese))

20 尼早,邱志平.結構系統概率--模糊--非概率混合可靠性分析.南京航空航天大學學報,2010,42(3):272-277(Ni Zao,Qiu Zhiping. Hybrid probabilistic fuzzy and non-probabilistic reliability analysis on structural system.Journal of Nanjing University of Aeronautics&Astronautics,2010,42(3):272-277(in Chinese))

21 Du XP,Sudjianto A,Huang BQ.Reliability-based design with the mixture of random and interval variables//ASME 2003 Design Engineering Technical Conference and Computers and Information in Engineering Conference(DETC2003),Chicago,IL,USA;2005

22 Du XP.Interval reliability analysis//ASME 2007 Design Engineering Technical Conference and Computers and Information in Engineering Conference(DETC2007),Las Vegas,NV,USA,2007

23 程遠勝,鐘玉湘,曾廣武.基于概率和非概率混合模型的結構魯棒設計方法.計算力學學報.2005,22(4):501-505(Cheng Yuansheng,Zhong Yuxiang,Zeng Guangwu.Structural robust design based on hybrid probabilistic and non-probabilistic models.Chin J Comput Mech,2005,22(4):501-505(in Chinese))

24 Luo YJ,Kang Z,Li A.Structural reliability assessment based on probability and convex set mixed model.Comput Struct,2009, 87(21-22):1408-1415

25 Kang Z,Luo Y.Reliability-based structural optimization with probability and convex set hybrid models.Structural and Multidisciplinary Optimization,2010,42(1):89-102

26 Jiang C,Lu GY,Han X,et al.A new reliability analysis method for uncertain structures with random and interval variables.Int J Mech Mater Des,2012,8(2):169-182

27 Jiang C,Han X,Li WX,et al.A hybrid reliability approach based on probability and interval for uncertain structures.ASME J Mech Des,2012,134(3):1-11

28 姜潮,鄭靜,韓旭等.一種考慮相關性的概率--區間混合不確定模型及結構可靠性分析.力學學報,2014,46(4):591-600(Jiang Chao,Zheng Jing,Han Xu,et al.A probability and interval hybrid structural reliability analysis method considering parameters’correlation.Chin J Theor App Mech,2014,46(4):591-600(in Chinese))

29 Jiang C,Zheng J,Ni BY,et al.A probabilistic and interval hybrid reliability analysis method for structures with correlated uncertain parameters.International Journal of Computational Methods,2015, 12(4):1540006,24

30 韓文欽,周金宇,孫奎洲.失效模式相關的機械結構可靠性的Copula分析方法.中國機械工程學報,2011,22(3):278-282(Han Wenqin,Zhou Jinyu,Sun Kuizhou.Copula analysis of structural systems reliability with correlated failure mode.Chinese Journal of Mechanical Engineering,2011,22(3):278-282(in Chinese))

31 Adduri PR,Penmetsa RC.Bounds on structural system reliability in the presence of interval variables.Computers and Structures,2007, 85(5-6):320-329

32 Qiu ZP,Yang D,Elishako ffI.Probabilistic interval reliability of structural systems.International Journal of Solids and Structures, 2008,45(10):2850-2860

33 Wang J,Qiu ZP.The reliability analysis of probabilistic and interval hybrid structural system.Applied Mathematical Modelling,2010, 34(11):3648-3658

34 Zhang Y,Der Kiureghian A.Two Improved Algorithms for Reliability Analysis,Reliability and Optimization of Structural Systems. Springer,1995:297-304

35 Yuan Y,Sun W.Optimization Theories and Methods.Beijing:Science Press,1997

36 張明.結構可靠度分析—方法與程序.北京：科學出版社,2009 (Zhang Ming.Structural Reliability Analysis:Methods and Procedures.Beijing:Science Press,2009(in Chinese))

38貢金鑫.工程結構可靠度計算方法.大連：大連理工大學出版社, 2003(Gong Jinxin.Computational Methods for Reliability of Engineering Structures.Dalian:Dalian University of Technology Press, 2003(in Chinese))

39 Pandey M.An e ff ective approximation to evaluate multinormal integrals.Structural Safety,1998,20(1):51-67

40 Genz A,Bretz F.Computation of Multivariate Normal and Probabilities.Berlin:Springer Science&Business Media,2009

41 Genz A.Numerical computation of multivariate normal probabilities.J Comput Graph Stat,1992,1(2):141-149

42 Tang L,Melchers R.Improved approximation for multinormal integral.Structural Safety,1986,4(2):81-93

43 Sheng Z,Xie SQ,Pan C.Probability Theory and Mathematical Statistics.Beijing:China Higher Education Press,2001.129-131

44 Hu Z,Du X.First order reliability method for time-variant problems using series expansions.Structural and Multidisciplinary Optimization,2015,51(1):1-21

45 Huang ZL,Jiang C,Zhou YS,et al.Reliability-based design optimization for problems with interval distribution parameters.Structural and Multidisciplinary Optimization,2016,1:1-16

A SYSTEM RELIABILITY ANALYSIS METHOD FOR STRUCTURES WITH PROBABILITY AND INTERVAL MIXED UNCERTAINTY1)

Liu Haibo Jiang Chao2)Zheng Jing Wei Xinpeng Huang Zhiliang
(Key Laboratory of Advanced Design and Simulation Technology for Special Equiqments Ministry of Education，College of Mechanical and Vehicle Engineering，Hunan University，Changsha410082，China)

There are a large number of inherently uncertain parameters in the problem of system reliability.Traditional system reliability analysis methods are usually based on the probability model assumption.Probability distribution function of uncertain parameters can be easily obtained with sufficient samples,but in practical engineering problems,it is often difficult to get the precise probability distribution function with limited data or test conditions.In this paper,the uncertain variables of the system based on sufficient information are taken as the random variables,while others with limited information can only be given variation intervals.This paper proposes a new system reliability analysis method for structures with probability and interval mixed uncertainty.Firstly,the minimum reliability index of each failure mode is obtained based on an efficient solution method.Then the system reliability model under multiple failure modes with probability and interval mixed uncertainty is provided.Considering the dependence between di ff erent failure modes of systems,a correlation coefficient matrix is obtained by the linear correlation calculated method.Finally,the maximum failure probabilities are calculated for series and parallel system.Three numerical examples show that the present methodcan e ff ectively deal with the system reliability problems of multiple nonlinear failure modes with probability and interval mixed uncertainty.Compared to the traditional probabilistic reliability analysis method,the presented method can ensure the security of system well and it only needs less uncertain information,and hence it seems suitable for reliability analysis and design of many complex engineering structures or systems.

system reliability,probability and interval mixed uncertainty,maximum failure probability,dependence of failure modes

TB114.3

A

10.6052/0459-1879-16-294

2016–09–09收稿，2016–11–21錄用,2016–11–29網絡版發表.

1)國家自然科學基金重大項目(51490662)、湖南省杰出青年基金(14JJ1016)和霍英東基金(131005)資助項目.

2)姜潮，教授，主要研究方向：現代設計技術，機械可靠性.E-mail：jiangc@hnu.edu.cn

劉海波,姜潮,鄭靜,韋新鵬,黃志亮.含概率與區間混合不確定性的系統可靠性分析方法.力學學報,2017,49(2):456-466

Liu Haibo,Jiang Chao,Zheng Jing,Wei Xinpeng,Huang Zhiliang.A system reliability analysis method for structures with probability and interval mixed uncertainty.Chinese Journal of Theoretical and Applied Mechanics,2017,49(2):456-466