基于改進的BP神經網絡的水面蒸發預測
李 俊(太原理工大學水利科學與工程學院,太原 030024)
水面蒸發作為水循環的一個重要環節,對水資源的合理開發、制定適當的灌溉制度起到十分重要的影響[1],因此對水面蒸發量進行預測能夠為農業活動的決策提供一定的依據。
現行預測水面蒸發量的方法有:多元線性回歸模型[2]、灰色預測模型[3]、RBF神經網絡模型[4]、BP神經網絡模型[5]等,水面蒸發量與各個因素之間存在著復雜的線性關系,所以使用多元線性回歸模型并不能很好地反映水面蒸發的這一特性,而灰色預測模型存在對背景值和初始值的規定是不盡合理的缺點[6],為了達到相同的精度要求,RBF神經網絡的實現結構復雜過BP神經網絡的,因此針對水面蒸發與預測因素之間存在非線性關系的特點,以及模型的簡潔性,本文使用BP神經網絡來對水面蒸發進行預測,同時為了改變以往使用BP神經網絡預測水面蒸發的過程中沒有對指標進行篩選,造成模型結構不必要的擴展,降低模型工作效率,因此本文使用灰色關聯理論對指標進行初步篩選,去除一些與水面蒸發相關性相對較弱的指標,從而減少預測模型的輸入,優化網絡結構。以往使用灰色關系法進行指標篩選時,只是主觀的確定一個關聯度閥值來對指標進行篩選,但并未對篩選后指標的合理性進行分析[7],存在很大的主觀性,因此本文使用方差來代表指標的信息[8],對海選指標與篩選后的指標的信息進行比較,從而得出篩選后的指標的信息持有度(簡稱此法為指標信息評價法),以此來對指標的合理性進行分析。
本文稱結合灰色關聯法、指標信息評價法與BP神經網絡的方法為改進的BP神經網絡法,以太原地區的水面蒸發預測為例進行預測演算,并對預測模型的合理性進行分析,以期驗證預測模型的合理性,為水面蒸發的預測提供參考。
1 模型介紹
按照上文的內容,本文按照灰色關聯法、指標信息評價法與BP神經網絡3個部分來對改進的BP神經網絡模型進行介紹。
1.1 灰色關聯法
灰色關聯度可以表示2個指標之間的密切程度[9],因此計算各個預測因子與被預測因子之間的關聯度,從而得出各個預測因子與被預測因子的密切程度。
設有n-1個預測因子,1個預測因子,共有m組數據,得到以下矩陣樣本:
(1)
式中:xi,j為第i組的第j個指標值(1≤j≤n-1);xi,n為第i組的預測值。
對預測因子與被預測因子標準化,以避免指標量綱的影響,按下式計算:
(2)
式中:yij為標準化后的指標值。
使用式(2)對式(1)中的每一個指標值進行標準化轉換后,可以得到以下矩陣:
(3)
通過式(4)求每一個預測因子與被預測因子對應預測因子的關聯度。
(4)
式中:k(ij)為預測因子yij與被預測因子yin對應指標的關聯度;λ一般取0.5。
接著使用式(5)求每個預測因子與被預測指標的關聯度。
(5)
根據各個預測因子的關聯度來進行排序(聯系度越大,聯系越密切)。
1.2 指標信息評價法
變異系數法中提出使用方差大小來表示指標攜帶信息的多少,從而對指標進行賦權[10]。同樣的,可以使用方差的大小來評定篩選后的指標是否發生信息丟失,從而對指標的合理性進行評價。具體方法如下。
根據式(5)計算得到的每個指標與被預測指標的關聯度,從高到低對各個預測因子進行排列,從而得到以下樣本矩陣[按照關聯度高低把矩陣式(3)前n-1列從左到右排列,最后一列為被預測因子與矩陣式(3)最后一列相同]。
(6)
式中:za,b為第a組的第b個指標值(1≤a≤n-1);yi,n為第i組的預測值。
使用預測因子的信息持有度Rb來表示篩選出的b個預測因子所持有的信息占原預測因子信息的百分比,由此敘述可得以下公式。
Rb=(Sb/Sn-1)×100%
(7)
式中:Sb與Sn-1與分別為矩陣式(6)中前b個預測因子的方差、矩陣式(6)中前n-1個預測因子的方差。
不斷地對b進行取值進行試算,當Rb大于M時,對應最小的b即是最優預測因子個數,前b個預測因子為最優預測因子。在主成分分析理論中,通常保留累計方差貢獻率達到70%~90% 的信息含量較大的主成分,表示全部原始指標信息的絕大多數得到了反映[11],借助此思想,且為保險起見,M取90%。
1.3 BP神經網絡
BP神經網絡是一種按誤差逆傳播算法訓練的多層前饋網絡[12]。同時其能夠反映被預測因子與預測因子之間的非線性關系,適合用于水面蒸發預測。
BP神經網絡的工作示意圖見圖1。從左到右的三列圓圈分別表示輸入層、隱含層、輸出層,分別說明如下。
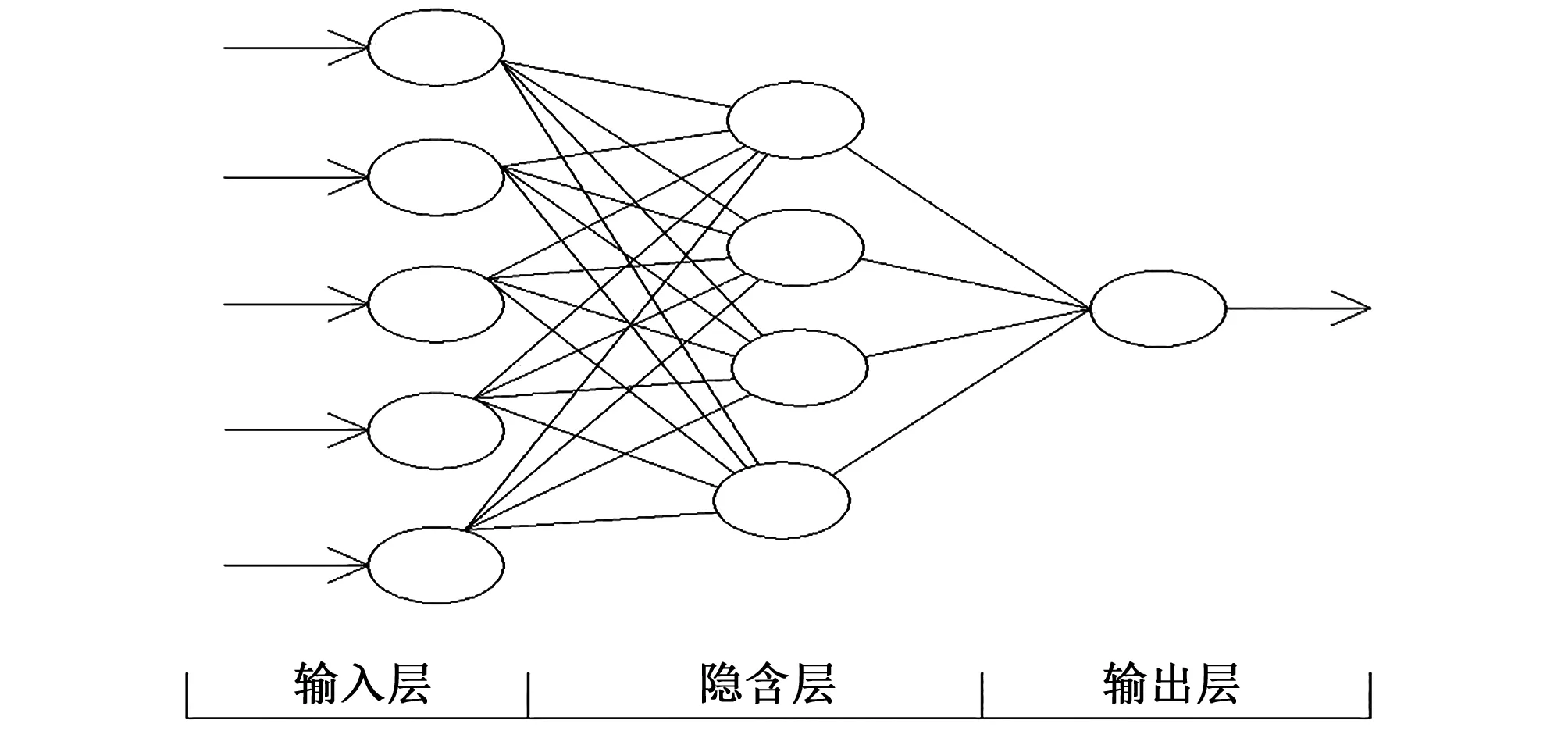
圖1 BP神經網絡工作示意圖Fig.1 Schematic diagram of BP neural network
輸入層:在本文中輸入層一般為預測因子,輸入層節點的個數也和最優預測因子個數相等。
隱含層:對以隱含層的節點數目前沒有統一的確定方法,一般取為輸入層節點數的75%[13],按照這個比例選取幾個可能的節點數進行試驗,最終確定最優隱含層的節點數。
輸出層:輸出層節點的個數和被預測因子個數相等,在本文中等于1。
在確定以上結構后,編寫程序,在Matlab R2013a中進行運算。
1.4 改進的BP神經網絡模型
綜合以上3部分,對改進的BP神經網絡模型的演算流程進行介紹,具體如下。
(1)使用灰色關聯法分別計算各個海選預測因子與被預測因子的關聯度,并按照關聯度大小從左到右對海選預測因子進行排列。
(2)使用指標信息評價法判定出最優預測因子組合。
(3)根據最優預測因子組合、BP神經網絡的結構特點與水面蒸發預測的特點定出BP神經網絡的結構,使用Matlab R2013a編程實現BP神經網絡算法。
(4)對結果進行合理性分析。
2 實例演示
本文選取太原地區為研究區域,收集2008年10月1日至2009年4月30日的逐日的平均氣壓、日最高氣壓、日最低氣壓、日最高氣溫、平均風速、最大風速、極大風速、日照時數、蒸發量作為基礎資料,其中選取平均氣壓、日最高氣壓、日最低氣壓、日最高氣溫、平均風速、最大風速、極大風速、日照時數為海選預測因子,蒸發量作為被預測因子。
由以上說明可知,在矩陣式(1)、式(3)、式(6)中m和n的取值分別為212、9。同時選擇2008-10-01-2009-03-31的數據作為訓練指標,而2009-04-01-2009-04-30的數據作為檢驗指標。具體數據見表1(應該展示的數據為2008年10月至2009年4月7個月的數據,但限于篇幅只是展示了2008年10月這一整個月的數據)。
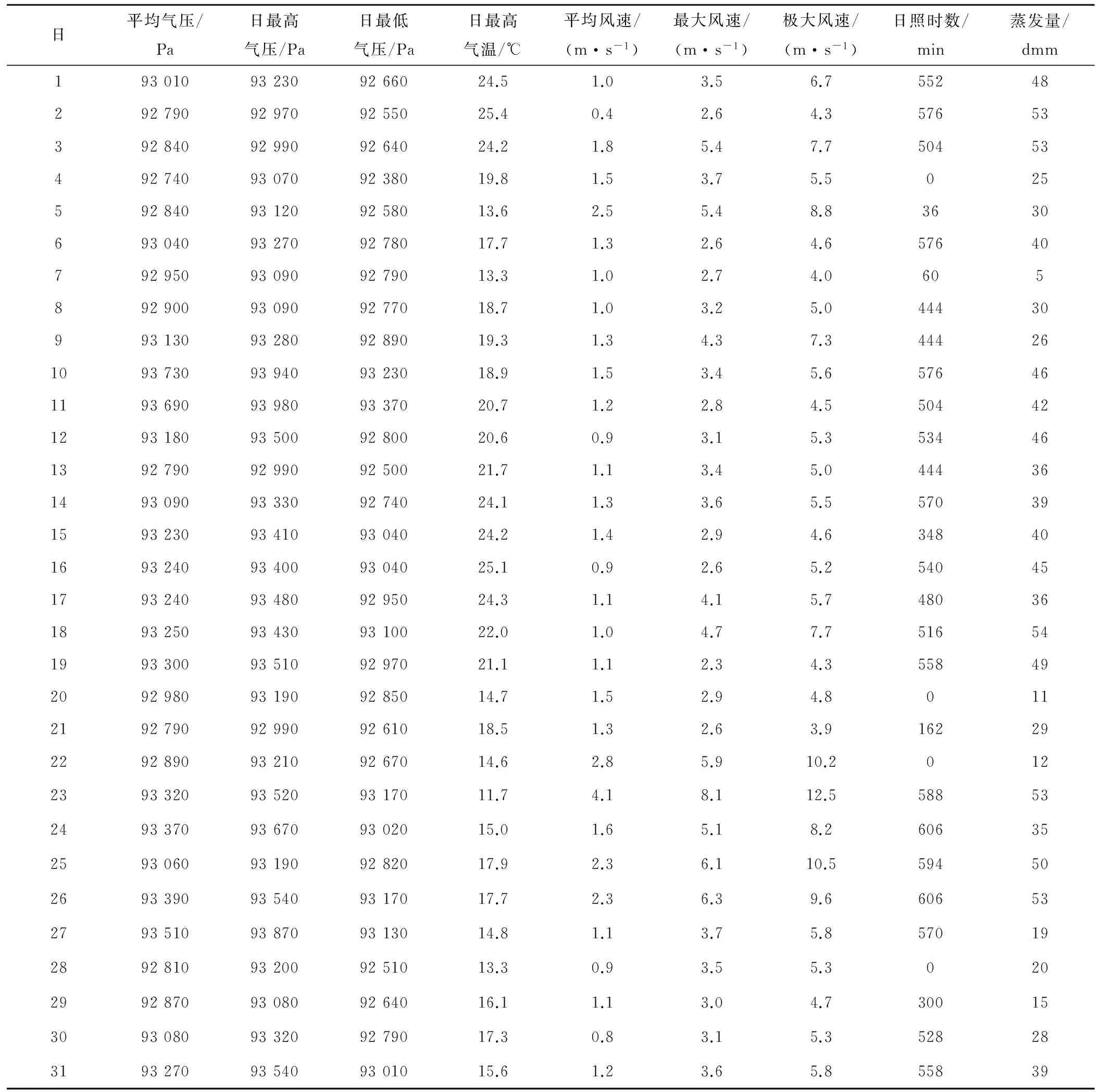
表1 示例數據表(2008年10月)Tab.1 Sample data sheet(2008.10)
注:表1中,使用了國際單位的表示方法,但在后文的計算中為了和收集的數據一致,所以后文的數據依然以使用原數據的單位表示,即平均氣壓、日最高氣壓、日最低氣壓、日最高氣溫、平均風速、最大風速、極大風速、日照時數、蒸發量的單位分別為:0.1 hPa、0.1 hPa、0.1 hPa、0.1 ℃、0.1 m/s、0.1 m/s、0.1 m/s、0.1 h、0.1 mm。
根據式(2)對表1的數據進行標準化,使用式(4)和式(5)計算各個預測因子與被預測因子的關聯度,結果見表2。
選取不同的b值帶入公式(7)進行試算,各個b值對應的信息持有度見表3。

表2 預測因子關聯度表Tab.2 Predictive factor correlation degree

表3 b值與Rb對應關系表Tab.3 Relationship between b and Rb
由表3可知Rb大于90%時,最小的b值為5,故最優預測因子為日最高氣溫、日照時數、極大風速、平均風速、最大風速。
由以上可得,在BP神經網絡中輸入層的節點數為5,經過對可能隱含層節點數的試驗,得出隱含層節點數為4,輸出層節點數為1,所以BP神經網絡的結構為5-4-1。
以日最高氣溫、日照時數、極大風速、平均風速、最大風速為預測因子,蒸發量為被預測因子。
同時選擇2008-10-01-2009-03-31的數據作為訓練指標,而2009-04-01-2009-04-30的數據作為檢驗指標。使用Matlab R2013a編程實現模型算法。檢驗結果見表4。

表4 檢查結果表(2009年4月)Tab.4 Result of checking(2009-04)
如果相對誤差絕對值小于20%算作合格的話[2],合格率等于(21/30)×100%=70%。
3 結 語
本文以太原地區的水面蒸發預測為例,使用結合灰色關聯法、指標信息評價法與BP神經網絡法的改進的BP神經網絡法對該研究區的水面蒸發進行預測,最后得出該模型的預報的合格率為70%。
灰色關聯法可以計算各個預測因子與被預測因子的關聯度,可以為指標的篩選作準備,同時使用指標信息評價法可以避免人為主觀確定關聯度閾值來選定最優最優預測因子的缺點,通過灰色關聯法與指標信息評價法來對指標進行篩選,可以減少BP神經網絡的輸入節點,優化BP神經網絡的結構,提高預測效率。
綜上可以得出該模型對于水面蒸發的預測具有一定適用性。
[1] 徐繼紅.干旱區影響水面蒸發的氣象因素多元回歸分析[J].水利規劃與設計,2016,(9):62-64.
[2] 魏光輝,董新光,楊鵬年,等.基于灰色關聯分析與多元線性回歸模型的水面蒸發預測[J].節水灌溉,2012,(2):41-44.
[3] 石麗忠,陳金良,遲道才,等.關于遼陽市水面蒸發量灰色預測模型的研究[J].節水灌溉,2007,(8):37-39.
[4] 魏光輝,馬 亮.基于灰色關聯分析與RBF神經網絡的水面蒸發量預測[J].干旱氣象,2009,27(1):73-77.
[5] 劉彩紅,馮宗友.基于BP神經網絡的新疆平原地區水面蒸發量預測模型研究[J].重慶工學院學報(自然科學版),2007,21 (6):87-89.
[6] 楊華龍,劉金霞,鄭 斌.灰色預測GM(1,1)模型的改進及應用[J].數學的實踐與認識,2011,41 (23):39-46.
[7] 薛 楠,鄔貽萍,鄶 晶.灰色關聯度在單病種質控指標篩選中的應用[J].中國衛生統計,1999,16 (3):181-182.
[8] 顧在浜,石寶峰,遲國泰.基于聚類—灰色關聯分析的綠色產業評價指標體系構建[J].資源開發與市場,2013,29(4):350-354.
[9] 劉 博,肖長來,田浩然,等.灰色關聯和層次分析法在地下水質評價中的應用----以吉林市為例[J].節水灌溉,2013,(1):26-29.
[10] 張小泓. 基于變異系數法的灰色關聯模型在節水灌溉工程投標方案優選中的應用[J].節水灌溉,2009,(8):54-56.
[11] 汪冬華.多元統計分析與SPSS 應用[M].上海:華東理工大學出版社,2010:192-215.
[12] 于 濤. BP網絡自適應學習率算法分析[D].大連:大連理工大學,2011:1-2.
[13] 唐啟義,馮明光. DPS數據處理系統[M].北京:科學出版社,2006:933-934.

