組距式分組下關于眾數計算問題的若干思考

曹潔+馬玲玲+焦榮榮

摘要：在教學過程中，經過對眾數的分析研究認為，在現行的統計學教材中就眾數的計算方法有值得商榷之處。

關鍵詞：眾數；組距式分組；連續式；間斷式

中圖分類號：G642.41 文獻標志碼：A 文章編號：1674-9324（2017）08-0201-02

統計中一旦收集了數據，第一步就是整理數據，也就是實用簡單的指標去描述數據。完成這一步最容易的方法就是計算幾種不同形式的集中趨勢（measures of central tendency），它能夠最好的代表一組數據的數值，一般具有三種形式：均值、中位數和眾數。

一、眾數的概念

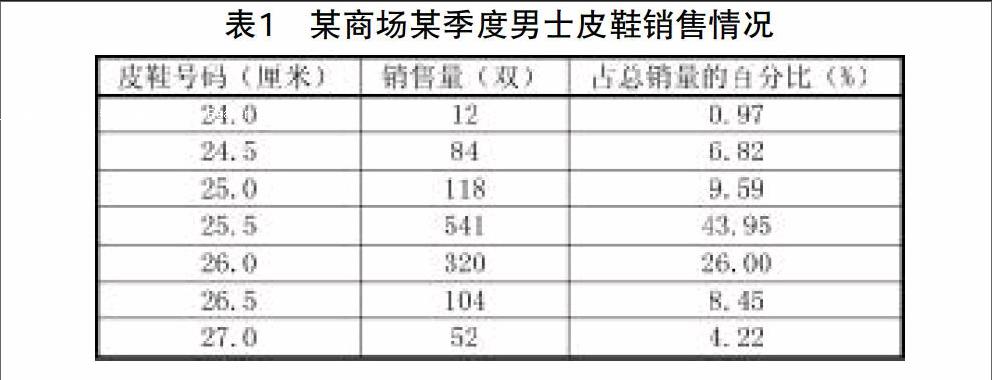
某制鞋廠要了解消費者最需要哪種型號的男士皮鞋，調查了某百貨商場某季度男士皮鞋的銷售情況，得到資料如表1。

從表1的資料可以看出，25.5厘米的鞋號銷售量最多。統計學中，把在一組數據當中出現次數最多的標志值就稱為眾數（mode），一般用M表示。眾數是位置平均數，它不受極端變量的影響，這是眾數區別于均值的一個重要標志。

眾數容易被人們“忽視”，因為人們仿佛總是更喜歡去記憶那些需要“計算”的事情，認為眾數只要被“數”出來就可以。眾數，的確是最籠統、最不精確的集中趨勢，但它卻在理解特定的數據分布中扮演著重要的角色。

二、眾數的重要性

毫無疑問，對于定性數據，類似種族群體、眼睛顏色、收入檔次等變量的集中趨勢只可以使用眾數來進行描述。例如，你不可能用中位數來描述哪個鞋碼在銷售中占有優勢，也不能使用均值——平均鞋碼為25.65厘米顯然是沒有實際意義的。而1231個人中幾乎一半（541）人的鞋碼是25.5厘米似乎是描述這個變量一般水平的最好的方式。再如，為了掌握市面上某種商品的價格水平，完全不必全面登記該商品的全部價格去計算其均值，因為均值很容易受到極端值的影響，只是需要用該商品成交量中最多的那個價格即價格的眾數作為代表值，就可以反映該商品價格的一般水平。

三、關于眾數的計算

就眾數的計算方法來看，現行的統計學教材中的處理值得商榷。

一般情況下，在給出所有數據或在對數據進行了單項式分組的情況下，直接找到頻數最大的變量值就是這組數據的眾數，但是在組距式分組的情況下，對于眾數的推算有以下的計算公式：

上限公式：M=U-d

下限公式：M=L+d

其中，U表示眾數所在組上限；L表示眾數所在組下限；Δ表示眾數所在組頻數與其下限的鄰組頻數的差；Δ表示眾數所在組頻數與其上限的鄰組頻數的差；d表示眾數所在組的組距。

由于一般的數據分布中眾數只有一個，所以上限公式和下限公式計算得到的眾數應當是一樣的，這一點非常重要。

例如：計算某班50名同學某一門課程成績的眾數，資料如表2所示。

其中，眾數所在的組為“66—69”這一組，U=69，L=66，Δ=20-10=10，Δ=20-13=7、d=3根據公式可得：

上限公式：M=69-×3≈67.76

下限公式：M=66+×3≈67.76

四、幾種特殊情況下眾數計算的探討

1.偏態分布。一組數據有如下分布（見表3），利用公式計算眾數。

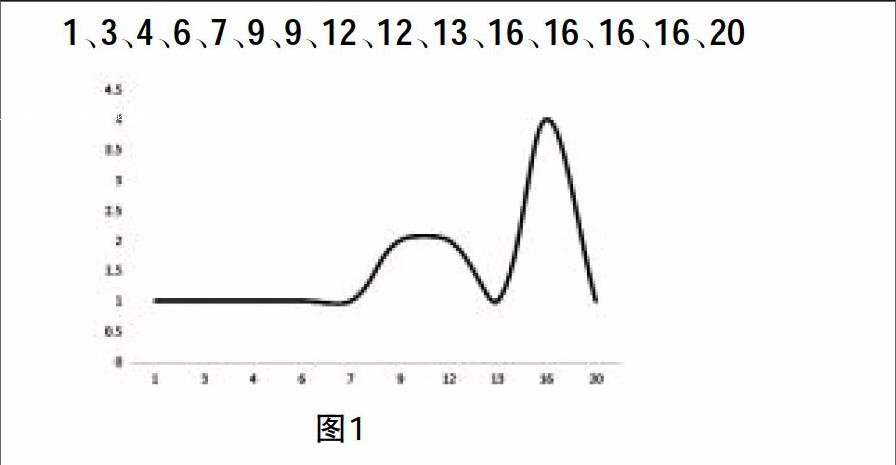
由分布情況可知，眾數所在的組為“9—13”這一組，按照公式進行計算，得到M=12.2。但是如果是這樣一組數據，具體如圖1所示。

1、3、4、6、7、9、9、12、12、13、16、16、16、16、20

顯然，這組數據符合表3中的數據分布情況，對于組距式分組，我們無法判斷它的眾數是什么，只能用眾數的計算公式對它的眾數進行一個估計和推斷。

2.間斷式組距式分組。雖然我們很不喜歡間斷式的組距式分組，但不可否認，它依然是存在的。比如剛才說的某班50名同學的成績，我們假設每一個學生的成績都沒有小數，于是，我可以對成績進行間斷式的組距式分組。

你能猜到出現了什么情況嗎？

上限公式：M=68-×3≈66.76

下限公式：M=66+×3≈67.76

是的，使用上限公式和下限公式所計算的結果出現了異常。對比后發現，除了眾數所在組的上限從69變到了68以外，公式里的其他條件都沒有發生變化。這又是為什么呢？首先能想到的原因就在于我們的間斷式分組上。我們都知道，如果分組是表2中的連續式分組，有一個原則叫做“上限不在內”，也就是說，在“66—69”中，上限69是沒有包含在這一組中的，而是變成了下一組的下限，那么反過來考慮，能不能認為在間斷式分組計算眾數公式時，M=U-d中的U其實就是下一組的下限呢？當然可以，并且我們已經得到了驗證。根據這種情況，我們給出在間斷式組距式分組下眾數的計算公式：

上限公式：M=L-d

下限公式：M=L+d

其中，L表示與眾數所在組后一組下限；L表示眾數所在組下限；Δ表示眾數所在組頻數與其下限的鄰組頻數的差；Δ表示眾數所在組頻數與其上限的鄰組頻數的差；d表示眾數所在組的組距。

當然，此時的組距應當是本組上限—前組上限。就是我們所說的間斷式分組的組距的計算方法。

還有其他的解釋嗎？讓我們把焦點放在公式中所涉及到的對象上面。之前提到，公式中“d”是眾數所在組的組距，也就是說，不管是連續式分組還是間斷式分組，眾數的計算只和眾數所在的那一組有關系，所以這時候，d就應該是68-66=2，此時，

上限公式：M=68-×2≈67.18

下限公式：M=66+×2≈67.18

不要再去糾結為什么兩種方式得到的眾數值不一樣，就像前邊解釋過的，我們通過公式計算出來的眾數只是實際眾數的一個近似值。

注釋：

（1）集中趨勢：是指一組數據向其中心值靠攏的傾向。

（2）均值：即算術平均數，是觀察值的總和除以觀察值總個數的商。

（3）中位數：將數據按照一定的順序排列，處于中間位置的數就是中位數。

（4）標志值：數量標志在各單位的具體表現數值。

（5）位置平均數：總體中處于特殊位置的個別單位的標志值。一般有眾數和中位數。

（6）定性數據：表示事物的品質特征，不能用數值表示，結果表現為類別。

（7）單項式分組：一個變量值為一組。

（8）組距式分組：將變量值一次劃分為幾個區間，每個區間為一組，每個變量值按其大小確定所屬的區間。

參考文獻：

[1]夏鷺平.統計學基礎[M].哈爾濱工程大學出版社，2014.

[2][美]薩爾金德.愛上統計學第二版[M].史玲玲，譯.重慶大學出版社，2011.