電路工作模式下惰性節點的確定
崔曉通 鄒敏輝 吳剴劼
(信息物理社會可信服務計算教育部重點實驗室(重慶大學) 重慶 400044)(重慶大學計算機學院 重慶 400044)(xiaotong.sd@gmail.com)
電路工作模式下惰性節點的確定
崔曉通 鄒敏輝 吳剴劼
(信息物理社會可信服務計算教育部重點實驗室(重慶大學) 重慶 400044)(重慶大學計算機學院 重慶 400044)(xiaotong.sd@gmail.com)
集成電路設計和制造的全球化趨勢使得木馬電路可以在集成電路設計制造的任何階段被插入,這引發了對硬件安全的廣泛關注.從防御者的角度出發,木馬電路在宿主電路使用過程中絕大多數時間是靜默無害的,但是一旦被激活就會造成如信息泄露、功能異常或系統崩潰等嚴重危害;從攻擊者的角度出發,避免木馬電路被“誤觸發”是其最重要的一個設計目標之一.普遍認為,電路中那些具有較低狀態翻轉概率的惰性節點最有可能成為木馬電路的插入點.因此目前檢測的主要手段之一是試圖尋找到這些惰性點,以便有針對性地嘗試以激活木馬電路.然而,目前的方法僅專注于尋找被測電路在測試模式下的惰性點.提出了一種尋找被測電路在工作模式下的惰性點的方法.從攻擊者的角度出發,兩者的交集將是木馬電路的最佳插入點——可以較好地避免其插入的木馬電路在宿主電路的測試階段以及試運行階段被“誤觸發”.因此從防御者的角度出發,找到測試模式和工作模式下共有的惰性節點并對其進行檢測,有助于有效提高檢測效率.
木馬電路;工作模式;惰性節點;狀態翻轉概率;總狀態
集成電路設計和制造的全球化使得集成電路的安全課題成為了重要的研究領域,這是因為,為了節約成本,集成電路在設計和制造過程中將部分任務分包給第三方制造商或者設計公司完成,這使得硬件木馬電路的植入成為可能[1-5].
硬件木馬電路可以在規范說明階段、設計階段、制造階段和測試階段在內的各個階段被插入[6];其通常由2部分組成:觸發電路和負載電路.當觸發電路在特定條件下被激活后,負載電路按照木馬設計者的意愿發揮作用,如通過旁信道泄露信息,或直接改變宿主電路的輸出,或為攻擊者提供遠程控制等[7].存在于關鍵性系統(如經濟、軍事、醫療等)中的木馬電路毫無疑問將會帶來重大安全隱患,因此木馬電路的檢測是一項十分重要的工作.
根據木馬電路的性質,通常對其檢測的方法有包括功耗、時間分析在內的旁道檢測技術[8],和通過有目的地產生測試向量以激活木馬電路的檢測技術[9],也可能是兩者的結合.
從攻擊者(即木馬電路設計者)的角度出發,“誤觸發”帶來的后果是災難性的,不僅沒有實現其破壞目的,且將給其代表的利益集團帶來經濟聲譽上的重大損失.木馬電路的“誤觸發”指的是其設計的木馬電路在非最佳場景下被激活并對宿主電路造成影響.由于這種影響通常大而明顯,很容易被宿主電路的監測機制捕獲,因此木馬電路通常只有一次機會對宿主電路造成危害,這使得避免木馬電路的誤觸發成為木馬電路設計的一個重要內容.
不難預見的一個經常會導致木馬電路誤觸發的情景是針對木馬電路的測試模式.在測試模式下,測試者通過向被測電路提供特定的測試向量以試圖激活被測電路中的木馬電路.另外一個重要的誤觸發場景是電路的工作模式——在電路的試運行過程或是正常工作過程中由于電路的正常輸入而誤觸發了木馬電路.雖然木馬電路的設計本意即是在工作狀態中激活并對宿主電路造成影響,但是必須考慮到木馬電路危害的一次性,在非最佳場景時被激活并不是木馬電路設計的初衷.首先,幾乎所有的關鍵任務一般多會有試運行階段.試運行的設計毫無疑問將會盡量模擬真實工作的各種情況.在試運行階段誤觸發木馬電路依然會暴露攻擊者的意圖但并沒有達到最佳攻擊意圖.其次,在電路的正常工作狀態下,未到達攻擊者最理想的工作場景(如特定的時間等)的情況下觸發木馬電路雖然會對系統造成一定的損害,但不一定是決定性的,因此也是誤觸發的一種.
為了避免誤觸發,木馬電路的設計者通常會利用宿主電路中的惰性節點來構建其木馬電路的觸發電路.電路的惰性節點是那些擁有較低的狀態翻轉概率的電路節點.因此,尋找惰性節點也是目前檢測木馬電路的一個主要方法.然而目前的工作僅考慮了測試模式下的惰性節點,如文獻[10].而在工作模式下的惰性節點卻被忽略.根據上述原因,我們認為,那些在2種模式下翻轉概率都比較低的惰性節點最有可能被利用來構建木馬電路的觸發電路.然而,如第1節所示,工作模式下電路節點狀態翻轉概率的計算完全不同于測試模式下的計算方法,因此準確地計算工作模式下節點的翻轉概率進而確定惰性節點是非常必要的.本文的主要工作是通過準確計算工作模式下電路節點的翻轉概率,結合測試模式的檢測結果,確定真正的電路惰性節點.
1 動機及示例
根據引言的描述我們知道,可以對電路節點的狀態翻轉概率進行計算進而可以判斷可能被攻擊者選中的木馬電路植入點.通常狀態翻轉概率低的電路節點具有更大的可能性成為植入點——將有效地降低木馬電路的誤觸發概率.因此,準確地計算電路節點的狀態翻轉概率對于木馬電路的檢測具有重要意義.文獻[10]研究了在測試模式下對電路節點的轉移概率進行計算進而確定電路中的惰性節點——那些在測試過程中狀態翻轉概率明顯較低的電路節點.在測試模式下,被測試電路中所有的寄存器通過掃描鏈組織,和測試電路的輸入一起受測試者的直接控制.因而每個寄存器和每個輸入的值均有同等概率為1或0,即50%為狀態1,50%為狀態0.不難看出,這樣的方式不僅沒有區分在工作模式時電路的常用和非常用輸入,而且更嚴重的是沒有區分被測試電路的非法狀態和合法狀態,以及狀態之間的非法和合法跳轉,因而測試模式下得到的惰性節點并不一定是工作模式下的惰性節點.下面通過示例來進一步說明這個問題.我們從一個有窮狀態自動機(finite state machine, FSM)開始,如圖1所示,其描述的是具有一個輸入和一個輸出的電路,當且僅當輸入的字符串為10101時,輸出為1,否則輸出為0.
以這樣一個有窮狀態機為基礎,接下來便是對狀態的編碼以及電路的設計與實現.從圖1可知,該狀態機除了初始狀態S0外還有S1,S2,S3,S4共4種狀態,考慮到設計和修改的簡單性以及易于檢測非法狀態,我們采用“一位熱碼編碼”(one-hot encoding)的方式對狀態進行編碼,并將S0,S1,S2,S3,S4分別編碼為0000,0001,0010,0100,1000,進而設計了帶有4個寄存器的電路,如圖2所示.

Fig. 1 The example of a FSM圖1 有窮狀態機示例
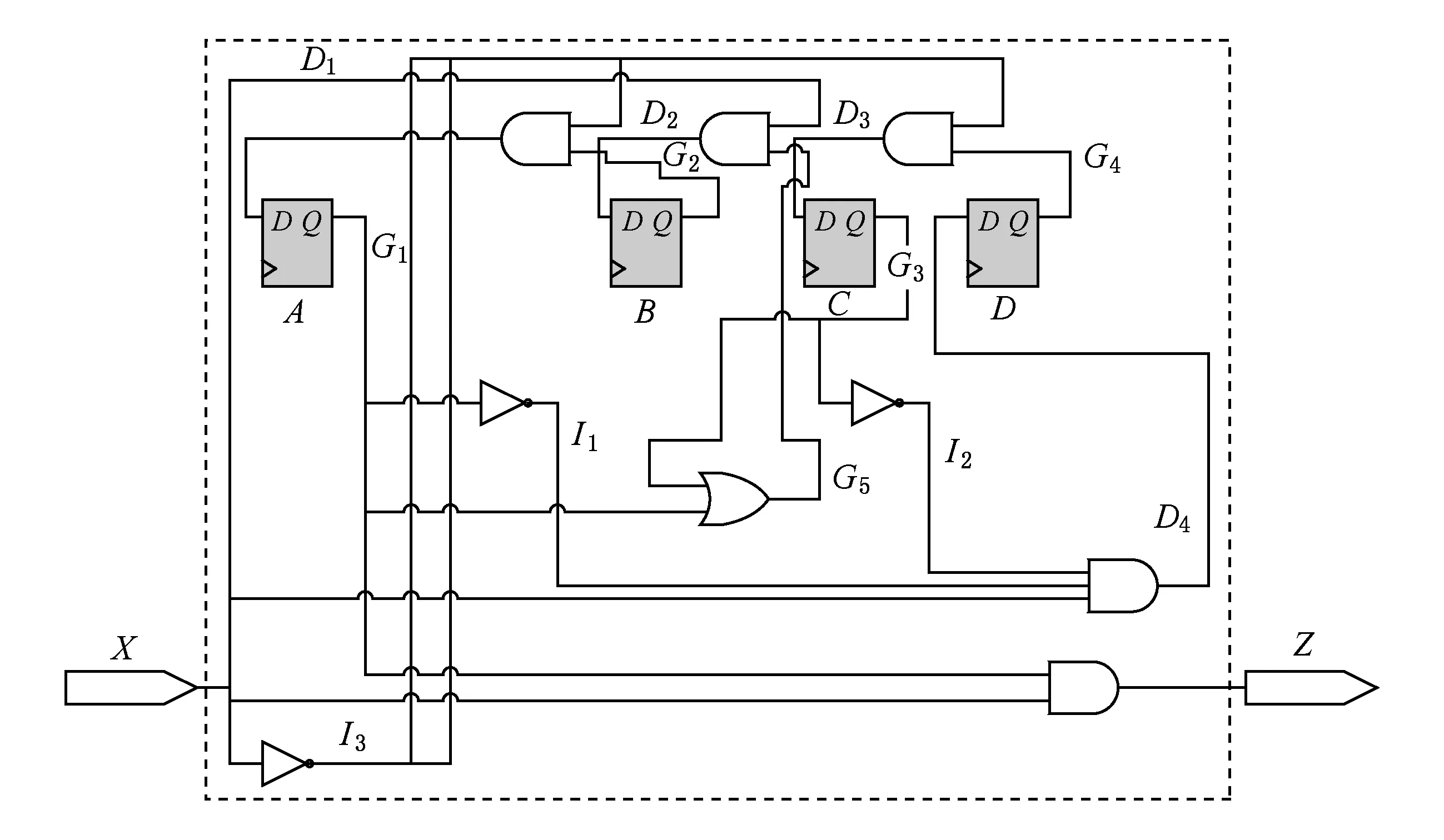
Fig. 2 The example circuit according to the FSM圖2 根據有窮狀態機設計的電路示例
按照文獻[10]中的計算方法,如果節點N的狀態翻轉概率為Pt(N:0→1)=Pt(N:1→0),節點N為0或1的概率分別為P(N=0)和P(N=1),那么Pt(N:0→1)=Pt(N:1→0)=P(N=0)×P(N=1).在文獻[10]中,如果節點N為電路的輸入(primary input),那P(N=0)=P(N=1)=0.5.如果該節點為某個邏輯門的輸出,那么根據邏輯門的種類,該節點為0或1的概率可以總結如下(假定該邏輯門的輸入為A和B):
1)N為反向器輸出
P(N=1)=P(A=0),P(N=0)=P(A=1);
2)N為與門輸出
P(N=1)=P(A=1)×P(B=1),P(N=0)=1-P(N=1);
3)N為與非門輸出
P(N=0)=P(A=1)×P(B=1),P(N=1)=1-P(N=0);
4)N為或門輸出
P(N=0)=P(A=0)×P(B=0),P(N=1)=1-P(N=0);
5)N為或非門輸出
P(N=1)=P(A=0)×P(B=0),P(N=0)=1-P(N=1).
根據這些來自文獻[10]的計算法則,圖3展示了圖2中部分電路節點的狀態概率.在圖3中,節點N的狀態概率以(P(N=0),P(N=1))表示.節點的狀態翻轉概率因此可以簡單計算出來.如,Pt(D4)=78×18=764.圖2示例電路中所有節點的狀態翻轉概率都可以通過這種方式計算得到,計算結果如表1第1行.
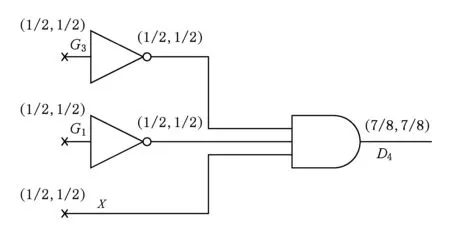
Fig. 3 The cone of the net D4圖3 節點D4的結構
然而,文獻[10]中的計算方法只適用于測試模式下電路節點狀態翻轉概率的計算.當電路在工作模式下,電路的狀態以及狀態跳轉并非是隨機的.因此,電路節點狀態翻轉概率的計算在工作模式下與在測試模式下是完全不同的.為了驗證我們的想法,我們以成千上萬比特的隨機輸入序列對電路的運行模式進行了模擬,統計了各節點的狀態翻轉概率并列于表1的第2行.
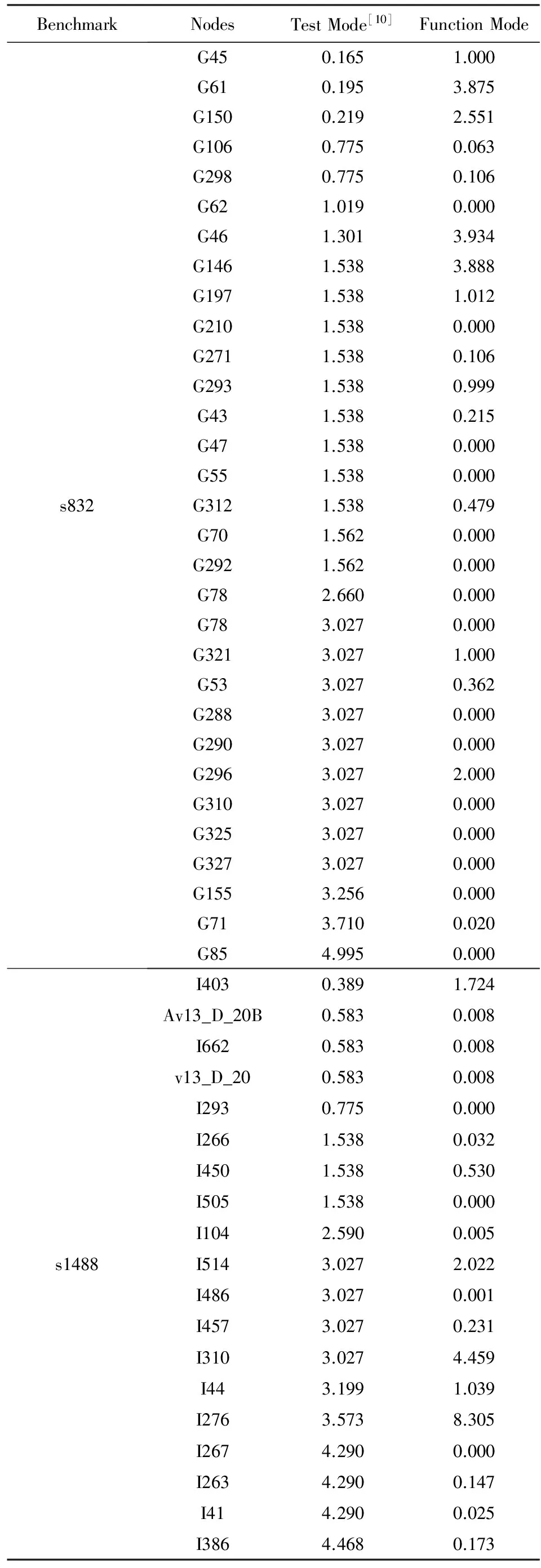
從表1中可以看出2個結論:1)2種模式下的同樣節點的轉移概率在大多數情況下有很大的區別,如I1,D1,Z等;2)電路節點間的相對活躍程度在2個模式下是不一致的.如在測試模式下Pt(D2)>Pt(D3),而在工作模式下Pt(D2) Table 1 Pt Comparison between Test Mode[10] and Function Mode Simulation 在本節我們提出了一種準確計算工作模式下電路節點狀態翻轉概率的方法,可以結合測試模式下各節點的狀態翻轉概率,更好地實現對木馬電路插入點的預測. 2.1 節點狀態翻轉概率的計算 根據圖1的有窮狀態機,我們可以得到其狀態轉移表,如表2所示: Table 2 State Transition Table of the Example Circuit 以圖3中D4節點為例,作為一個三輸入與門的輸出,D4從1轉換為0的概率是所有的輸入(X,I1,I2)在當前狀態下都為1,且在下一個狀態有至少一個輸入變為0的概率.更進一步地,跟蹤所有決定D4的電路輸入和寄存器{G1,G3,X},D4從1轉換為0的概率相當于{G1,G3,X}從{0,0,1}轉換到{0,0,0},{0,1,0},{1,0,0},{1,1,0},{0,1,1},{1,0,1},{1,1,1}中的一種概率之和.其中G1和G3來自狀態寄存器,X是電路的輸入.也就是說,D4從1轉換到0的概率Pt(D4:1→0)為下面所有概率之和: Pt(D4:1→0)= Pt({G1,G3,X}:001→000)+ Pt({G1,G3,X}:001→010)+ Pt({G1,G3,X}:001→011)+ Pt({G1,G3,X}:001→100)+ Pt({G1,G3,X}:001→101)+ Pt({G1,G3,X}:001→110)+ Pt({G1,G3,X}:001→111). 以Pt({G1,G3,X}:001→000)為例,D4從1轉換到0的條件發生于: 1) 在轉換之前{G1,G3}={0,0},X=1; 2) 在轉換之后{G1,G3}={0,0},X=0. 因此可以知道,計算節點的狀態翻轉概率需要電路的狀態和輸入的共同信息.因此,我們用stateinput表示一個電路的總狀態TS(total state),那么Pt(TS:S1i1→S2i2)表示了電路在總狀態TS=S1i1和總狀態TS=S2i2之間的轉移概率.根據電路的有窮狀態機且假設隨機的電路輸入X,即P(X=0)=P(X=1)=0.5,可以推出其總狀態轉移概率矩陣M,如圖4所示: S0∕0S0∕1S1∕0S1∕1S2∕0S2∕1S3∕0S3∕1S4∕0S4∕1S0∕00.50.500000000S0∕1000.50.5000000S1∕0000.50.5000000S1∕100000.50.50000S2∕00.50.500000000S2∕10000000.50.500S3∕0000.50.5000000S3∕1000000000.50.5S4∕00.50.500000000S4∕10000000.50.500 Fig. 4 Total state transition matrix M of the example circuit 顯而易見,節點的狀態翻轉概率將和電路的總狀態的轉移概率相關.根據表2和圖4,可以得到: Pt({G1,G3,X}:001→000)= Pt(TS:S01→S10)+Pt(TS:S11→S10)+ Pt(TS:S31→S40)= Pt(TS=S01)×0.5+P(TS=S11)×0.5+ P(TS=S31)×0.5=(P(TS=S01)+ P(TS=S11)+P(TS=S31))×0.5. 因此Pt({G1,G3,X}:001→000)的概率依賴于P(TS=S01),P(TS=S11)和P(TS=S31).下面介紹電路的總狀態的概率計算方法. 2.2 電路中各個總狀態概率的計算 在工作模式下,電路的狀態由其有窮狀態自動機決定.有窮狀態自動機和輸入序列將共同控制到達各個狀態的概率,不斷增加的輸入最終將使各個狀態趨于一個穩定狀態[11],即到達各個狀態的概率將趨于一個穩定的值.因此我們用 V=(v1=P(TS=S00),v2=P(TS=S01), v3=P(TS=S10),v4=P(TS=S11), v5=P(TS=S20),v6=P(TS=S21), v7=P(TS=S30),v8=P(TS=S31), v9=P(TS=S40),v10=P(TS=S41)) 來表示示例中穩定狀態的概率向量,假設總狀態總數為S,則: (1) 根據穩定狀態的特性有: V×M=V. (2) 根據式(1)(2),可以求得V=(0.125,0.125,0.187 5,0.187 5,0.093 75,0.093 75,0.062 5,0.062 5,0.031 25,0.031 25). 進而我們可以得到(2.1節中): Pt({G1,G3,X}:001→000)= (P(TS=S01)+P(TS=S11)+ P(TS=S31))×0.5=0.187 5; Pt({G1,G3,X}:001→010)=0; Pt({G1,G3,X}:001→011)=0; Pt({G1,G3,X}:001→100)=0; Pt({G1,G3,X}:001→101)=0; Pt({G1,G3,X}:001→110)=0; Pt({G1,G3,X}:001→111)=0. 將以上所有的概率加起來,我們得到D4在工作模式下的狀態轉移概率Pt(D4:1→0)=0.187 5.用同樣的方式,我們可以得到示例電路工作模式下所有節點的狀態轉移概率,將它們與電路工作模式下模擬得到的結果(表1第2行)相比,如表3所示: Table 3 Pt Comparison between Simulation and our Method of the Example Circuit 運用高斯消除法[12]根據式(1)(2)計算穩定狀態向量時間復雜度為O(N2),其中N為狀態總數.然而對于大規模的電路,總的狀態數目隨著輸入和狀態的比特數呈指數增長,構造一個完整的狀態轉移概率矩陣M或者穩定狀態向量V是不可行的.在我們的方法中,我們提出通過盡可能多的大量輸入并記錄所有狀態及狀態轉移,運用統計的方法推斷出M和V.比如,M中的某一個值可以通過統計所得的轉移次數與總時鐘節拍數的比率來求得,穩定狀態下各個狀態的概率也可以用類似的方法得到.沒有監測到的狀態轉移以及其穩定狀態的概率被設為0.由于我們求取M和V的初衷就是觀察工作模式下狀態轉移的頻繁程度,因此這種統計的方法有非常好的效果. 我們的算法目的是為了找到所有電路內部節點的狀態翻轉概率.如果某節點是寄存器,其狀態翻轉概率可以從總狀態轉移概率矩陣M來決定.因此這里我們將集中討論那些非寄存器的內部節點,即那些由組合邏輯門直接輸出的電路節點,如示例電路中I1,I2,I3等節點.如果將電路的所有總狀態的集合定義為TSet,對于節點i,TSet可以分為2個子集Set1(i)和Set0(i),它們分別表示可以使該節點的輸出為1和0的總狀態集合.它們之間有如下關系: Set1(i)∪Set0(i)=TSet, 且: Set1(i)∩Set0(i)=?, Set1(i)和Set0(i)可以由i驅動門的類型和驅動門各輸入的Set0和Set1來決定. 算法1. 尋找Set1(i)和Set0(i). ① 初始化所有的Set1 andSet0為NULL; ②Find_Sets(i){ ③ ifi是一個主輸入then ④ returnSet1(i) andSet0(i);*請看算法描述* ⑤ end if ⑥ for節點i的驅動門的每個輸入j ⑦Find_Sets(j); ⑧ end for ⑨ 計算Set1(i)和Set0(i); ⑩ returnSet0(i)和Set1(i).} 算法1以節點i以及其所有輸入為輸入,輸出Set1(i)和Set0(i).算法1行①初始化所有節點的Set1(i)和Set0(i)為空;行②~⑩調用函數Find_Sets(i);行③~⑤,如果節點i是一個電路輸入或寄存器,則它的Set1(Set0)是除了其本身為1(0)其余輸入和寄存器位為任意項;行⑥~⑧,對于節點i的每項輸入j,遞歸調用Find_Sets(j);行⑨當找到節點i的驅動門的所有輸入狀態集合之后,Set1(i)和Set0(i)可以通過以下規則進行計算: 1) 如果i的驅動門是只有一個輸入j的反相器,則: Set1(i)=Set0(j); Set0(i)=Set1(j); 2) 如果i的驅動門是一個輸入為jk(k>1)的與門,則: Set1(i)=∩Set1(jk); Set0(i)=TSet-Set1(i); 3) 如果i的驅動門是一個輸入為jk(k>1)的與非門,則: Set0(i)=∩Set1(jk); Set1(i)=TSet-Set0(i); 4) 如果i的驅動門是一個輸入為jk(k>1)的或門,則: Set0(i)=∩Set0(jk); Set1(i)=TSet-Set0(i); 5) 如果i是一個輸入為jk(k>1)的或非門,則: Set1(i)=∩Set0(jk); Set0(i)=TSet-Set1(i). 最后行⑩返回得到Set0(i)和Set1(i). 算法2. 計算SP(i). ①Pt(i)=0; ② forSet1(i)中的每個總狀態 ③ forSet0(i)中的每個總狀態 ④ 在矩陣M中找到對應的翻轉概率P; ⑤ 在向量V中找到對應的v; ⑥Pt(i)+=P×v; ⑦ end for ⑧ end for 算法2是計算節點i的狀態翻轉概率SP(i).節點i的狀態發生翻轉的充要條件是電路從Set1(i)中的某個總狀態轉移到Set0(i)中的某個總狀態,或者從Set0(i)中的某個總狀態轉移到Set1(i)中的某個總狀態.因此,節點i的狀態翻轉概率的計算原理是計算從Set1(i)中的每個總狀態轉移到Set0(i)中的每個總狀態的概率之和.首先,行①將節點i的翻轉概率Pt(i)賦值為0;行②~⑧,對于Set1(i)中每個總狀態到Set0(i)中的每個總狀態的轉移在總狀態轉移矩陣中找到對應的轉移概率P,并和穩定狀態概率v中對應的概率P相乘,累加到Pt(i). 我們用Nnet,Npri,Ndff分別代表一個電路的節點個數、主要輸入個數和狀態寄存器的個數. 算法1的時間復雜度:考慮最壞的情況,計算節點i需要遞歸遍歷到所有節點,每個節點有N個輸入,每個輸入都和所有的主要輸入和狀態寄存器相關,則算法1的時間復雜度為Nnet×2n×(Npri+Ndff). 算法2的時間復雜度:假設最壞的情況,節點i的Set1(i)和Set0(i)中各有2Ndff+Npri個總狀態,則算法2的時間復雜度為22(Ndff+Npri). 我們對7組基準測試程序作了實驗,它們都來自于ISCAS89電路基準測試程序[13].對于每組基準測試程序,我們都用文獻[10]中測試模式的計算方法、工作模式下我們的方法計算所有節點的狀態翻轉概率,并報告狀態翻轉概率小于5%的節點的交集,實驗結果表4所示: Table 4 Inactive Nets in both Test Mode and Function Mode Continued (Table 4) Continued (Table 4) 集成電路設計和制造的全球化趨勢使得木馬電路可以在集成電路設計制造的任何階段被插入,這引發了對硬件安全的廣泛關注.從防御者的角度出發,木馬電路在宿主電路使用過程中絕大多數時間是靜默無害的,但是一旦被激活就會造成如信息泄露、功能異常或系統崩潰等嚴重危害.從攻擊者的角度出發,避免其插入的木馬電路被“誤觸發”是其最重要的一個設計目標之一.普遍認為,電路中那些具有較低狀態翻轉概率的惰性節點最有可能成為木馬電路的插入點.因此目前檢測的主要手段之一是試圖尋找到這些惰性點,以便有針對性地嘗試以激活木馬電路.然而,目前的方法僅專注于尋找被測電路在測試模式下的惰性點.本文提出了一種尋找被測電路在工作模式下的惰性點的方法.從攻擊者的角度出發,兩者的交集將是木馬電路的最佳插入點——可以避免其插入的木馬電路在宿主電路的測試階段和試運行階段被“誤觸發”;從防御者的角度出發,兩者的交集將大大降低需要檢測的電路節點,有助于提高檢測效率.在文章的最后,我們報告了7組來自于ISCAS89的電路基準測試程序在測試模式和工作模式下具有狀態翻轉概率小于5%的節點的交集. 進一步工作為:算法1和算法2的時間復雜度并非是多項式時間內可以完成的,尤其在電路規模比較大的時候,其計算時間隨寄存器以及電路輸入的位數呈指數增長,只能解決小到中規模的電路(如僅有幾十個輸入和狀態寄存器).并且在計算構造一個完整的狀態轉移概率矩陣M和穩定狀態向量V時需要大量的隨機輸入,某些非惰性節點會被誤判成惰性節點.我們觀察到,在實際的電路中,只有一些狀態寄存器對電路輸入敏感(造成電路狀態跳轉),很多狀態寄存器對電路輸入不敏感(不造成電路狀態跳轉).因此我們進一步的工作將致力于電路工作模式下節點翻轉概率計算的啟發式算法的研究,利用某些狀態寄存器對電路輸入不敏感這個重要的觀察,以使得在基本保持計算精度的條件下極大地減少計算開銷. [1]Abramovici M, Bradley P. Integrated circuit security—New threats and solutions[C]Proc of the 5th Annual Workshop on Cyber Security and Information Intelligence Research: Cyber Security and Information Intelligence Challenges and Strategies. New York: ACM, 2009: 55:1-55:3 [2]Chakraborty R S, Narasimhan S, Bhunia S. Hardware Trojan—Threats and emerging solutions[C]Proc of High Level Design Validation and Test Workshop. Piscataway, NJ: IEEE, 2009: 166-171 [3]Jin Y, Kupp N, Makris Y. Experiences in hardware Trojan design and implementation[C]Proc of IEEE Int Workshop on Hardware-Oriented Security and Trust. Piscataway, NJ: IEEE, 2009: 50-57 [4]Cui Xiaotong, Ma Kun, Shi Liang, et al. High-level synthesis for run-time hardware Trojan detection and recovery[C]Proc of the 51st Annual Design Automation Conf. Piscataway, NJ: IEEE, 2014: 1-6 [5]Tehranipoor M, Koushanfar F. A survey of hardware Trojan taxonomy and Detection[J]. IEEE Design & Test Computers, 2010, 27(1): 10-25 [6]Karri R, Rajendran J, Tehranipoor M. Trustworthy hardware: Identifying and classifying hardware Trojans[J]. Computer, 2010, 43(10): 39-46 [7]Bhunia S, Abramovici M, Agrawal D, et al. Protection against hardware Trojan attacks: Towards a comprehensive solution[J]. IEEE Design & Test, 2013, 30(3): 6-17 [8]Cha B, Gupta S K. Trojan detection via delay measurements: A New approach to select paths and vectors to maximize effectiveness and minimize cost[C]Proc of Design, Automation & Test in Europe Conf & Exhibition (DATE). Piscataway, NJ: IEEE, 2013: 1265-1270 [9]Fang Lei, Li Lei, Li Zhen. A practical test patterns generation technique for hardware Trojan detection[J]. Elektrotehniki Vestnik, 2013, 80(5): 266-270 [10]Salmani H, Tehranipoor M, Plusquellic J. A novel technique for improving hardware Trojan detection and reducing Trojan activation time[J]. IEEE Trans on Very Large Scale Integration Systems, 2012, 20(1): 112-125 [11]Wikipedia. Markov chain[EBOL]. [2015-09-27]. http:en.wikipedia.orgwikiMarkov_chain [12]Wikipedia. Gaussian elimination[EBOL]. [2015-09-27]. http:en.wikipedia.orgwikiGaussian_elimination [13]Wikipedia. ISCAS89 sequential benchmark circuits[EBOL]. [2015-09-27]. https:filebox.ece.vt.edu~mhsiaoiscas89.html Cui Xiaotong, born in 1991. Received his BS degree in computer science and technology from Chongqing University, China, in 2013. PhD candidate in computer science and technology at the College of Computer Science, Chongqing University. His main research interests include real-time task scheduling and hardware security. Zou Minhui, born in 1989. Received his BS degree in computer science and technology from Chongqing University, China, in 2013. PhD candidate in computer science and technology at the College of Computer Science, Chongqing University. His main research interests include security of cryptographic system and side-channel attacks. Wu Kaijie, born in 1974. Received his BE degree from Xidian University, Xian, China, in 1996, his MS degree from the University of Science and Technology of China, Hefei, China, in 1999, and his PhD degree in electrical engineering from Polytechnic University (Now Polytechnic Institute of New York University), Brooklyn, New York, in 2004. He then joined University of Illinois, Chicago, USA as an assistant professor. Since 2013, he becomes a professor at the College of Computer Science, Chongqing University, China. Member of the IEEE and CCF. His main research interests inchlude the big area of trustworthy computing with special interest on dependable computing and hardware security. Identifying Inactive Nets in Function Mode of Circuits Cui Xiaotong, Zou Minhui, and Wu Kaijie (KeyLaboratoryofDependableServiceComputinginCyberPhysicalSociety(ChongqingUniversity),MinistryofEducation,Chongqing400044)(CollegeofComputerScience,ChongqingUniversity,Chongqing400044) The globalization trend of design and manufacture of IC raises serious concerns about hardware security since there is possibility that in each phase of design and manufacture hardware Trojan can be inserted. From the defender’s perspective, hardware Trojan in the host circuit may stay inactive for most of time but will result in disastrous consequences once activated, such as information leakage, false output, system crash, etc. As far as an attacker concerned, one of important design criteria is to prevent the Trojan circuit from being accidently activated. It is believed that inactive nets with lower switching probabilities in the circuit are more likely to be selected as the trigger signals of Trojan circuits. Hence finding these inactive nets is one of the existing countermeasures. However, current techniques only focus on finding inactive nets in test mode of the circuit. This paper proposes a method that can find inactive nets in function mode of the testing circuit. From an attacker’s point of view, the nets that are inactive in both test mode and function mode are the best candidates for Trojan triggers—it will result in the lowest probability of accidental activation of Trojan circuits in both modes. Hence for a defender, focusing on these nets will improve the efficiency of Trojan detection significantly. hardware Trojan; function mode; inactive nets; switching probabilities of states; total states 2015-10-27; 2016-03-22 國家自然科學基金項目(61472052);國家“八六三”高技術研究發展計劃基金項目(2015AA015304,2013AA013202) This work was supported by the National Natural Science Foundation of China (61472052) and the National High Technology Research and Development Program of China (863 Program)(2015AA015304, 2013AA013202). TP331.1
2 工作模式下電路節點狀態翻轉概率的計算



圖4 示例的總狀態轉移概率矩陣M
3 算法及其復雜度
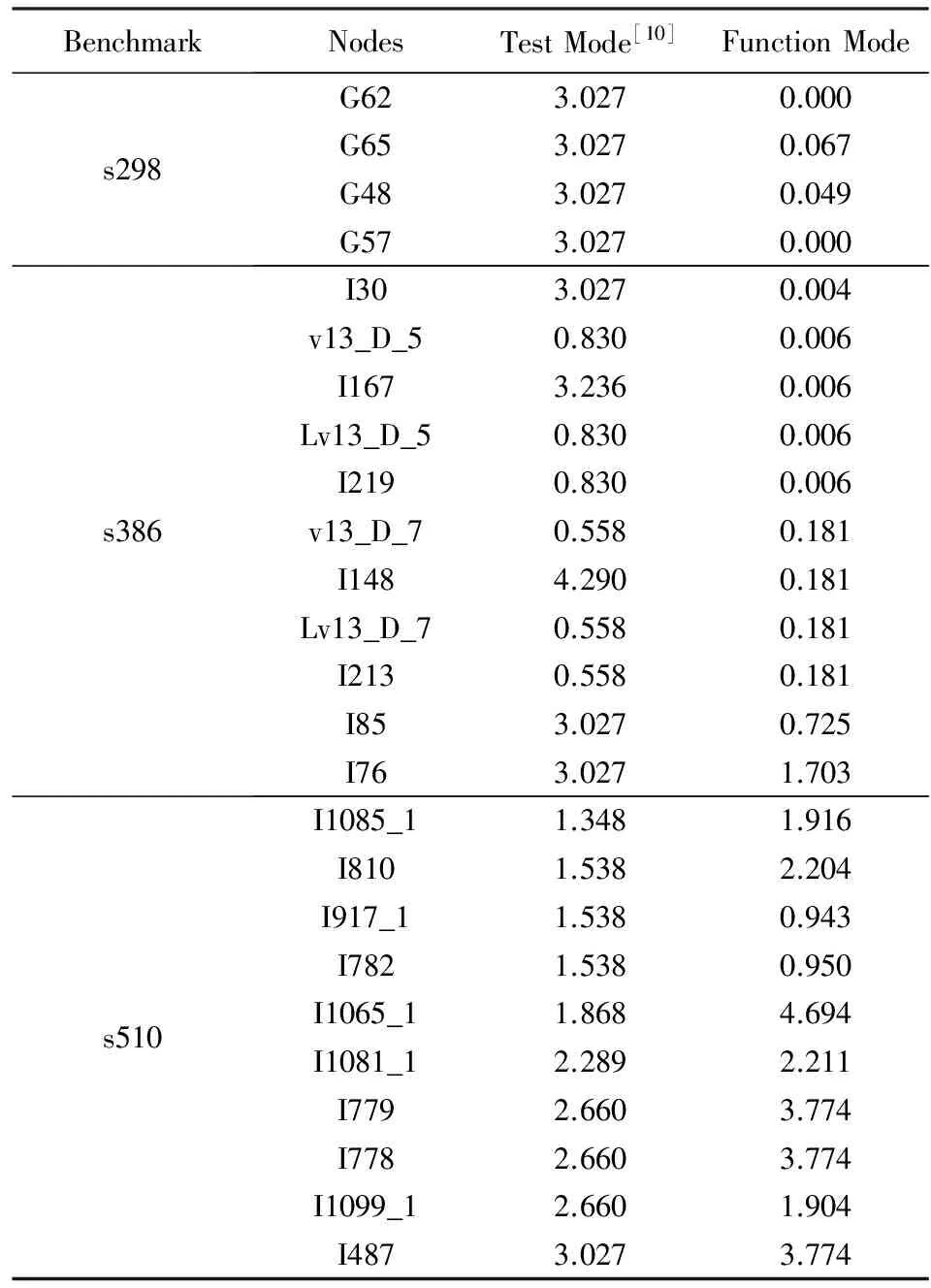
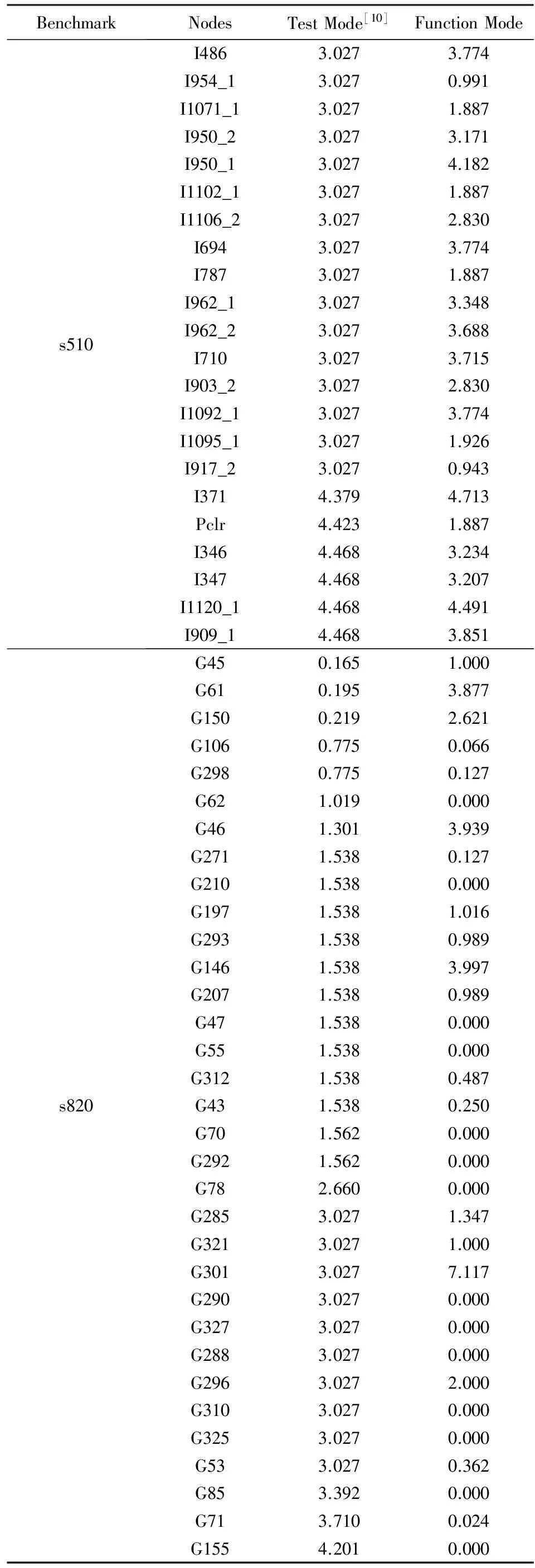
4 實 驗
5 結論及進一步工作



