火炮彈藥協調器區間不確定參數辨識
趙搶搶,侯保林
(南京理工大學 機械工程學院, 江蘇 南京 210094)
火炮彈藥協調器區間不確定參數辨識
趙搶搶,侯保林
(南京理工大學 機械工程學院, 江蘇 南京 210094)
火炮彈藥協調器是一個復雜的多參數機電液一體化系統,在建立其動力學模型時,某些對系統性能有重要影響的不可測或難以測量的參數,只能通過辨識的方法獲得。為了實現彈藥協調器的參數辨識,在Simulink中建立彈藥協調器的動力學模型與控制模型,并利用區間數描述系統動作過程中的不確定參數;利用區間序關系轉換模型,將存在區間不確定參數的辨識問題轉換成確定性優化問題進行求解;以協調器支臂角速度曲線的相似度作為優化目標,利用差分進化算法實現了彈藥協調器的參數辨識;利用仿真數據確定了此方法的辨識精度滿足要求,并利用測試數據對真實系統的參數進行了辨識,驗證了此方法的可行性和有效性。
兵器科學與技術;火炮;彈藥協調器;參數辨識;區間優化;相似度分析;差分進化算法
0 引言
彈藥協調器是大口徑自行火炮彈藥自動裝填系統的一個重要部件,主要用于接收彈倉內被推彈器推送出來的彈丸,再將該彈丸傳輸到輸彈線上,由輸彈機輸彈入膛[1]。其在武器裝備服役使用過程中,時常發生定位精度超差的情況,嚴重降低了整個彈藥自動裝填系統的可靠性,亟待進行改進設計。建立其準確的動力學模型,對于推斷協調器在運行過程中系統特性的變化情況,進而根據系統特性的變化情況提出改進設計建議,乃至實現故障診斷和預測,都具有重要的意義。
建模過程中的一個核心問題是系統參數的確定,協調器作為一個復雜且多參數的機、電、液一體化系統,其中某些參數是已知的,可通過計算或測試獲得;某些是未知且難以測量的,但在系統某次確定的動作循環中,由于動作時間短,可近似認為是確定的,可通過辨識的方法獲得;然而,還有一類不確定參數,其真實值即使是在某次確定的動作循環過程中也是變化的,當前的認知手段無法確定其明確的分布規律,但可以確定其變化的區間范圍,其他不確定數學方法用來描述這類參數時都存在或多或少的不足,而區間數則可以很好的描述這類參數的不確定性[2]。
根據Ljung[3]的定義,辨識由數據、模型類和準則3個要素組成。其中數據是辨識的基礎,準則是辨識的依據,模型類是辨識的范圍,辨識就是按照一個準則在一組模型類中選擇一個對數據擬合得最好的模型。因此辨識問題可看作是一個優化問題,利用尋優的方法求解。在傳統的確定性優化方法中,決策的判斷都是基于目標函數和約束在各個設計向量處的具體數值,然而,當用區間數描述系統的不確定參數時,對于任一待辨識的參數,由于不確定參數為一區間數,因此目標函數的可能取值都構成一個區間,無法通過傳統的確定性優化方法求解[4]。針對這類存在參數區間不確定的優化問題,一般是通過合適的方法將其轉化為確定性問題進行求解。程志強等[5]根據過程工業系統的特點,將區間多目標優化問題轉化為一個極大極小問題,并結合遺傳算法和非線性規劃方法,分析了上述轉化的可行性;蔣崢等[6]針對區間單目標非線性優化問題,引入決策風險因子和偏差懲罰項,將區間非線性規劃問題轉化成一個確定型極大極小問題,并采用遺傳算法以遞階優化的方式求解;Jiang等[7]采用區間分析方法計算目標函數的區間值,將上述問題轉化為確定性多目標優化問題進行求解。總體來說,現在對于區間不確定問題的研究主要集中在如何將其轉換為確定性問題進行求解,而對于其工程應用的研究還較少。
本文為解決存在區間不確定參數的火炮彈藥協調器的參數辨識問題,根據協調器的結構和控制原理,在Simulink中建立了協調器的動力學模型和仿真模型;利用區間序關系轉換模型,將區間不確定性問題轉換為確定性問題進行求解;考慮到協調器的可測響應量為支臂的角速度,將測試曲線與辨識曲線的相似度作為差分進化算法的適應度函數,即優化目標函數,利用差分進化算法對協調器的參數進行辨識。
1 彈藥協調器建模
1.1 協調器的動力學建模
彈藥協調器的結構如圖1(a)所示,由兩個并聯的串勵電機驅動,減速箱由兩級直齒輪傳動和一級蝸輪蝸桿傳動組成,其中蝸輪與火炮耳軸固聯;小平衡機由平衡油缸和蓄能器組成,用于平衡彈藥協調器的重力矩,減小驅動電機的負載,支撐協調器平穩運動;彈藥協調器設置有角位移傳感器和角速度傳感器(測速度電機),用于提供協調器相對于起落部分的角度信號,使協調器轉至正確位置[1]。

圖1 彈藥協調器結構及工作原理Fig.1 Structure and working principle of shell transfer arm
彈藥協調器的工作原理如圖1(b)所示,它是一個單自由度系統,通過進行受力分析,可得到其動力學方程為
(1)
式中:θ為協調器的轉角;i1為系統總的傳動比;i2為齒輪3到蝸輪的傳動比;i3為蝸桿到蝸輪的傳動比;η1為齒輪1、2之間的傳動效率;η2為齒輪3、4之間的傳動效率;η3為蝸輪蝸桿的傳動效率;I01為電機和齒輪1的等效轉動慣量;I23為齒輪2、3的等效轉動慣量;I45為齒輪4和蝸桿的等效轉動慣量;I6為蝸輪、支臂和彈丸的等效轉動慣量;Td為電機的驅動力矩;TR為小平衡機對支臂的支反力矩;TG為支臂的重力矩。
TG取決于支臂的轉角,
TG=Lmgcos(θ+α),
(2)
式中:L為支臂質心到協調器旋轉中心的距離;m為支臂和彈丸的質量;α為支臂處于水平位置時,支臂質心到旋轉中心連線與水平線之間的夾角。
TR取決于油缸的壓力和支臂的轉角,其中油缸壓力為
p=p0S[V0/(V0-ΔV)]n,
(3)
式中:p0、S為蓄能器的初壓和油缸活塞面積;V0為氣體初始容積;ΔV為氣體變化的體積;n為氣體的多變指數。
則平衡機對協調器的作用力矩為
TR=lp0S[V0/(V0-ΔLS)]n,
(4)
式中:l為協調器旋轉中心至小平衡機的距離;ΔL為活塞運動的距離。
1.2 電機及控制系統建模
彈藥協調器由兩個并聯的串勵電機驅動,相關的動態方程[8]為
(5)
式中:U為電機電壓;E為反電動勢;R為電機電阻;I為電樞電流;L為電感;Φ為主磁通量;K為勵磁系數;Ce、CT分別為反電動勢系數和電磁轉矩系數;ω為電機轉速;T為電機輸出轉矩。
彈藥協調器的控制系統只對達到穩態值所需的時間和定位精度有要求,而對系統的暫態特性沒有要求,因此在實際設計系統時需兼顧的各種參數較少,其運動過程可簡化為如圖2所示的示意圖。圖2中,A1A2為協調器的運動范圍,協調器按要求從A3點運動到A4點,則整個運動過程可分為兩段:在A3A5段,只需控制電機的運動方向,給電機加額定電壓,使電機全速運動帶動協調器快速向A4點運動;當協調器運動到A5點,系統變成一個完全的閉環位置系統,把協調器準確定位在A4點,其速度曲線如圖3所示。

圖2 協調器運動及定位過程示意圖Fig.2 Schematic diagram of motion and location procedure of shell transfer arm

圖3 協調器動作過程的速度曲線Fig.3 Angular velocity curve of shell transfer arm
電機的速度是通過驅動電路改變電機電樞上的電壓平均值來控制的,電壓為準脈沖形式,在功能上類似于脈寬調制。為了實現電機的正轉與反轉,電機含有兩個方向相反的勵磁繞組。為了簡化驅動電路,功率元件采用絕緣柵雙極型晶體管(IGBT)。控制信號由比例- 微分閉環控制產生,當控制信號為正時,與正向勵磁繞組連接的IGBT導通;當控制信號為負時,與反向勵磁繞組連接的IGBT導通。同時,在觸發電路中設置了門限電路,使得IGBT的導通具有遲滯性,以防止兩個勵磁繞組同時接通。
根據上述分析,在Simulink中建立的協調器的動力學模型與控制模型如圖4所示。

圖4 彈藥協調器的動力學模型與控制模型Fig.4 Dynamic and control models of shell transfer arm
1.3 彈藥協調器參數分類
由1.2節建模過程可知,彈藥協調器模型包含的參數眾多。在一次動作過程中,其中某些參數是可通過計算或測量的方式獲得的,如等效轉動慣量I01、I23、I45、I6;某些參數是不確定的,無法得知其確定的值,也無法確定其準確的分布規律,只能確定其變化的區間。對于彈藥協調器而言,兩個區間不確定的參數分別為:
1)蝸輪蝸桿的傳動效率η3. 蝸輪蝸桿的傳動效率η3=ηnηsηz,其中ηs為考慮攪油損耗時的效率,取值范圍0.94~0.99,ηz為軸承效率,滾動軸承取值范圍0.98~0.99;ηn為嚙合效率,蝸桿為驅動元件時,ηn=tanγ/tan (γ+ρv),其中γ為導程角,ρv為當量摩擦角。ρv與齒面的相對滑動速度有關,而蝸輪蝸桿的相對滑動速度是隨協調器的轉速變化的。
2)蝸輪蝸桿的傳動比i3. 由于傳動系統間隙及機械構件受載變形等因素的影響,齒輪及蝸輪蝸桿傳動存在空回現象。由1.1節的建模過程可知,系統總的傳動比i1,齒輪3到蝸輪的傳動比i2都與蝸輪蝸桿的傳動比i3有關,因此本文在處理傳動空回問題時,將空回對整個傳動系統的影響等效在蝸輪蝸桿的傳動比i3上。空回非線性遲滯模型為[9]
(6)
式中:B為空回量;θm為驅動端轉角;θn為從動端轉角;t-、t+分別表示控制過程發生的前后時刻。由(6)式可知,傳動比與空回量B相關,而通常情況下空回量B是不確定的。
還有一類參數是未知的,且難以通過測量的方式獲得,但這些參數在一次動作過程中可近似地看做確定的,可通過辨識的方法獲得的。協調器模型中,3個待辨識參數為:
1)蓄能器的初始壓力p0. 小平衡機是通過氣囊式蓄能器提供動力的,蓄能器壓力的變化直接影響到油缸壓力的變化,從而導致協調器運行的不穩定。
2)測速電機的靈敏度k. 測速電機的靈敏度直接影響協調器的定位精度,但火炮射擊時的振動、溫度的變化、電磁干擾等都將導致靈敏度的異常。
3)氣體的多變指數n. 蓄能器在充壓過程中,氣體的多變指數是個不確定的數值,在其他參數都相同的情況下,多變指數不同,會使蓄能器的儲油量發生明顯的變化。
2 協調器參數辨識問題描述及其求解方法
本文的彈藥協調器參數辨識問題可作為一個優化問題來求解,即:在η3和i3在區間范圍內變化的情況下,尋找出最優的p0、k和n,使得模型的輸出與真實系統的輸出最接近。其數學模型為
(7)
式中:X為設計向量,X=(p0,k,n);D為不確定向量,D=(η3,i3);f為目標函數,是通過辨識獲得的協調器角速度曲線與測試所得角速度曲線的相似度;上標I、L和R分別表示區間、區間下界和區間上界。
對于任一確定的設計向量X,由于D的取值范圍為一區間量,因此目標函數f(X,D)可能取值也構成一個區間。而在傳統的確定性優化方法中,決策的判斷都是基于目標函數和約束在各個設計向量處的具體數值,因此,上述問題無法通過傳統的確定性優化方法進行求解。為此,本文利用區間序關系將不確定目標函數轉換成確定性問題進行求解。
2.1 基于區間序關系的不確定目標函數轉換
根據區間數理論[2],區間數被定義為一對有序的實數:
AI=[AL,AR]={x|AL≤x≤AR,x∈R},
(8)
式中:AI、AL、AR分別表示區間、區間下界和區間上界。區間數也可以通過中點Ac和半徑Aw來定義為
AI=〈Ac,Aw〉={Ac-Aw≤x≤Ac+Aw,x∈R},
(9)
式中:Ac=(AL+AR)/2,Aw=(AR-AL)/2.
AI≤LcBI,AL≤BL且Ac≤Bc.
(10)
基于(10)式表述的區間序關系≤Lc,可以通過目標函數區間的中點和下界來判斷不同設計向量之間的優劣:若設計向量X2優于X1,則X2處的目標函數區間優于X1處的目標函數區間,即fL(X2)≥fL(X1)且fc(X2)≥fc(X1)。因此,希望找到一個最優的設計向量,使得不確定目標函數的區間具有最大的中點值和下界,則(7)式中的不確定目標函數可轉換為如下的確定性多目標優化問題:
(11)
式中:對于任一X,需基于不確定目標函數的區間計算其下邊界與中點值。此處可通過兩次優化過程求解不確定目標函數的區間[10]:
(12)
根據上述轉換關系,(7)式表示的不確定優化問題可轉換為如下的確定性優化問題:
(13)
為了方便后續算法對其進行求解,此處采用線性加權法將(13)式轉換為一單目標優化問題[11]:
(14)
式中:fd為多目標評價函數;β的取值范圍為[0,1],為多目標權重,本文中β=0.5;ξ為保證fL(X)+ξ和fc(X)+ξ非負的參數,由于相似度本身為非負數,因此此處ξ=0;φ和ψ為多目標函數的正則化因子,可通過如下優化過程獲得
(15)
2.2 時間序列曲線相似度計算
(7)式中,目標函數為通過辨識獲得的協調器角速度曲線與測試所得角速度曲線的相似度S,相似度S的范圍為[0 1]。S=0表示兩個系統一切特性都不同;S=1表示兩個系統一切特性均相同;0 對于兩個時間序列數值曲線Y=[y1,y2,…,yn]和Y′=[y′1,y′2,…,y′n],其相似度S由數值相似度Sns與形狀相似度Sss組成。根據多屬性多指標綜合理論[13],組合相似度用乘法關系求取比用加法關系求取更合理,則相似度S可表示為 基于區塊鏈的新型IoT技術還處在“萌芽”階段,對學術界與工業界來說既是機遇又是挑戰。區塊鏈與IoT兩種技術的融合勢必會推動IoT安全的迅猛發展,并由此帶來技術的巨大升級。研究適合IoT特征的區塊鏈安全防護技術是未來的一種趨勢,但也存在各種挑戰而任重道遠。 (16) 數值相似度Sns利用相對誤差的加權平均值來表示: (17) 式中:si為各點的相似度, (18) δi為任意點的權重,用該點幅值占所有采樣點幅值和的比值表示為 (19) (20) (21) 式中:L(·)表示時間序列的長度;m為相似子序列的個數。 計算出Sns和Sss之后,即可根據(16)式計算得到兩時間序列曲線的組合相似度S. 2.3 差分進化算法 差分進化算法(DE)是一種模擬自然界生物種群以“優勝劣汰,適者生存”的隨機啟發式搜索算法,是一種新興的進化計算技術。DE具有待定參數少,不易陷入局部最優解,以及收斂速度快等特點。DE是基于實數編碼的進化算法,由變異、交叉和選擇3個基本操作構成,其主要步驟[15]如下: 1)生成初始種群。在N維空間里根據(22)式隨機產生滿足約束條件的M個個體: (22) 2)變異操作。對于每個目標向量xij,DE根據(23)式進行變異: hij(t+1)=xp1j(t)+F(xp2j(t)-xp3j(t)), (23) 式中:xp1、xp2和xp3為從群體中隨機選取的個體,i≠p1≠p2≠p3;F為變異因子,一般可選F為0.3~0.6. 3)交叉操作。為增加群體的多樣性,需進行交叉操作,具體操作如下: (24) 式中:CR?[0,1],為交叉概率。 4)選擇操作。為了確定xi(t)是否為下一代的成員,對于最大化問題,DE對實驗向量vi(t+1)與目標向量xi(t)的適應度函數進行比較,并根據(25)式進行選擇: (25) 式中:f為相應的適應度函數,本文中f為時間序列曲線的相似度S. 3.1 彈藥協調器角速度測試 在進行辨識之前,需對協調器的角速度進行測試,本文利用CS-ARS-02單軸陀螺儀對其進行測試。CS-ARS-02的量程為±200°/s,輸出電壓為[0 5] V,分辨率≤0.15 °/s,采樣頻率1 000 Hz. 多次測量的結果如圖5(b)所示,從圖5(b)中可以看出,測試的結果保持了很好的一致性,證明測試結果是可靠的。此處需要說明的是,在協調器定位階段,即700 ms之后,協調器的角速度曲線存在明顯的振蕩,這是由于彈丸在托彈盤中的振動導致的,而仿真模型中彈丸是不存在振動的,因此,在計算曲線相似度時,只取前700 ms的數據,而忽略了700 ms之后的數據。 圖5 測試過程與結果Fig.5 Test procedure and results 3.2 彈藥協調器的參數辨識 本文利用DE算法實現彈藥協調器的參數辨識,辨識過程如下: 1)設置DE算法的參數,在合理范圍內初始化種群,利用拉丁超立方采樣法,在i3和η3的區間內進行采樣,產生不確定參數i3和η3; 2)調用Simulink程序,對于種群中每個個體,結合i3和η3的采樣結果進行仿真,獲得協調器的角速度曲線族; 3)計算仿真所得角速度曲線與目標角速度曲線的相似度,得到相似度的區間范圍,根據(14)式計算得到fd,即DE算法的適應度函數; 4)根據(22)式~(25)式對種群個體進行交叉、變異和選擇操作; 5)重復步驟2~步驟4,直到達到最大迭代步數或預設的精度要求,輸出最終的最優解,即為辨識結果。 DE參數設置如下:種群個數30,變異因子F=0.7,交叉因子CR=0.6,最大迭代次數G=50. 待辨識參數搜索范圍為:蓄能器初壓p0[2.8 MPa,3.5 MPa],測速電機靈敏度k[0.6,1.1],氣體多變指數n[1.2,2.0]。不確定參數η3和i3的范圍分別為[0.47,0.6]和[59,61],拉丁超立方采樣個數50. 由于待辨識的參數是不可測或難以測量的,本文利用仿真實驗來確定此方法的辨識精度,利用測試數據對彈藥協調器的參數進行辨識,以驗證此方法的可行性。 表1給出了相應的辨識結果。其中,3組仿真數據中,DE算法對3個待辨識參數辨識結果的平均相對誤差分別為0.810 8%、1.487 0%及0.891 8%,可見辨結果的精度較高,滿足實際需求;對于圖5(b)中的4組測試數據,3個待辨識參數辨識結果的均值分別為3.025 2 MPa、0.997 2及1.498 7,均方差分別為0.010 0 MPa、0.006 9及0.010 2. 其均方差較小,表明辨識結果保持了較好的一致性,且3個待辨識的參數皆與理論值相符。圖6是將測試數據的辨識結果平均值代入Simulink模型中計算得出的支臂角速度與測試數據的對比,從圖6中可以看出,兩者的相似度較高,表明辨識結果是合理的。 表1 辨識結果Tab.1 Identified results 圖6 測試結果與辨識結果對比Fig.6 Comparison of test data and identified data 彈藥協調器是一個復雜的機電液一體化系統,某些參數往往不能明確地給出其具體數值或分布規律,而只能給出其區間范圍。針對利用區間數來描述參數不確定的情況,本文研究了基于DE算法和時序曲線相似度分析的參數辨識方法,獲得了以下結論: 1)建立了彈藥傳輸機械的動力學模型和控制模型,并在Simulink中進行求解。 2)利用區間序關系轉換模型,將具有參數區間不確定的辨識問題轉化成確定性優化問題進行求解。將時序曲線的相似度作為優化目標,利用DE算法實現了存在區間不確定參數的彈藥協調器參數辨識。 3)由于待辨識的參數是不可測或難以測量的,本文利用仿真實驗確定了此方法的辨識精度滿足要求。同時,利用測試數據對彈藥協調器的參數進行辨識,驗證了此方法是可行性。 References) [1] 侯保林, 樵軍謀, 劉琮敏. 火炮自動裝填[M]. 北京: 兵器工業出版社, 2010. HOU Bao-lin, QIAO Jun-mou, LIU Cong-min. Ammunition automatic loading system of howitzer[M]. Beijing: Publishing House of Ordnance Industry, 2010. (in Chinese) [2] Alefeld G, Herzberger J. Introduction to interval computations[M]. N Y: Academic Press, INC, 1983. [3] Ljung L. System Identification[M]. Boston: Spring, 1998. [4] 姜潮. 基于區間的不確定性優化理論與算法[D]. 長沙:湖南大學, 2008. JIANG Chao. Uncertainty optimization theory and algorithm based on interval number[D]. Changsha: Hunan University, 2008. (in Chinese) [5] 程志強, 戴連奎, 孫優賢. 區間參數不確定系統優化的可行性分析[J]. 自動化學報, 2004, 30(3): 455-459. CHENG Zhi-qiang, DAI Lian-kui, SUN You-xian. Feasibility analysis for optimization of uncertain systems with interval parameters[J]. Acta Aytomatica Sinica, 2004, 30(3): 455-459. (in Chinese) [6] 蔣崢, 戴連奎, 吳鐵軍. 區間非線性規劃問題的確定化描述及其遞階求解[J]. 系統工程理論與實踐, 2005, 25(1): 110-116. JIANG Zhen, DAI Lian-kui, WU Tie-jun. Deterministic interpretation of interval nonlinear programming and its hierarchical optimization solution[J]. Systems Engineering-Theory & Practice, 2005, 25(1): 110-116. (in Chinese) [7] Jiang C, Han X, Guan F J, et al. An uncertain structural optimization method based on nonlinear interval number programming and interval analysis method[J]. Engineering Structures, 2007, 29(11): 3168-3177. [8] 李紅偉. 串勵電機特性模擬與分析[J]. 微電機, 2010, 43(8): 95-97. LI Hong-wei. Characteristic simulation and analysis of series motor[J]. Micromotors, 2010, 43(8): 95-97. (in Chinese) [9] Su C Y, Stepanenko Y, Svoboda J, et al. Robust adaptive control of a class of nonlinear systems with unknown backlash-like hysteresis[J]. IEEE Transactions on Automatic Control, 2000, 45(12): 2427-2432. [10] 馬龍華. 不確定系統的魯棒優化方法及應用研究[D].杭州: 浙江大學, 2002. MA Long-hua. Research on method and application of robust optimization for uncertainty system[D]. Hangzhou: Zhejiang University, 2002. (in Chinese) [11] 孫曉輝, 丁曉紅. 結構多目標拓撲優化設計[J]. 機械設計與研究, 2012, 28(4): 1-4,9. SUN Xiao-hui, DING Xiao-hong. Research on multi-objective topology optimization design methods for structure[J]. Machine Design and Research, 2012, 28(4): 1-4, 9. (in Chinese) [12] 何江. 基于混合動態仿真的發電機模型有效性評估及參數校正研究[D]. 重慶: 重慶大學, 2011. HE Jiang. Research on validity evaluation and parameter calibration of generator model based on hybrid dynamic simulation[D]. Chongqing: Chongqing University, 2011. (in Chinese) [13] Xu Z H. Uncertain multi-attribute decision making: methods and applications[M]. Heidelberg : Springer, 2015. [14] 楊玉良, 秦俊奇, 狄長春, 等. 火炮動力后坐實驗臺建模及射擊模擬準確度評估[J]. 振動與沖擊, 2014, 33(10): 127-130. YANG Yu-liang, QIN Jun-qi, DI Chang-chun, et al. Modeling and firing simulation accuracy assessment of a gun-power-recoil test table[J]. Journal of Vibration and Shock, 2014, 33(10): 127-130. (in Chinese) [15] Price K, Storn R M, Lampinen J A. Differential evolution: a practical approach to global optimization[M]. Heidelberg: Springer, 2006. Identification of Interval Uncertainty Parameters of a Howitzer Shell Transfer Arm ZHAO Qiang-qiang, HOU Bao-lin (School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China) Shell transfer arm is a complicated mechatronic and hydraulic integrated system of howitzer with multi-parameters. During the modeling process, some parameters are hard or unable to be measured but have significant effect on the performance of shell transfer arm, which can only be achieved by identification. For identifying the parameters of shell transfer arm, the dynamic and control models are built in Simulink, and the uncertainty parameters are described by interval number. The identification problem of interval uncertainty parameters is transformed into a certainty optimization problem via order relation of interval number transformation model. The similarity of angular velocity of shell transfer arm is set as the optimization objective function, and three parameters are identified by differential evolution (DE) method. The proposed method is verified by simulated and test data. The identification results of simulated data show that the identification accuracy satisfies the requirement, and the identification results of test data show that the proposed method is feasible and effective. ordnance science and technology; howitzer; shell transfer arm; parameter identification; interval optimization; similarity analysis; differential evolution method 2016-06-28 國家“973”計劃項目(6132490102); 國家自然科學基金項目(51175266) 趙搶搶(1987—), 男, 博士研究生。 E-mail: zqqlzl@139.com 侯保林(1965—), 男, 教授, 博士生導師。 E-mail: houbl@njust.edu.cn TJ303+.3 A 1000-1093(2017)01-0035-08 10.3969/j.issn.1000-1093.2017.01.005
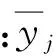


3 系統測試與參數辨識



4 結論

