火炮多柔體動力學結構優化研究

蕭輝，楊國來，孫全兆

(南京理工大學 機械工程學院, 江蘇 南京 210094)

火炮多柔體動力學結構優化研究

蕭輝，楊國來，孫全兆

(南京理工大學 機械工程學院, 江蘇 南京 210094)

針對現有動力學優化方法很難對多體系統中的柔性體進行結構優化的問題，提出結合多學科代理模型法和改進的非支配排序遺傳算法的多柔體動力學優化方法。以火炮炮口振動參數為輸出，柔體模態參數和部分火炮總體參數為輸入，在已驗證的多體剛柔耦合模型的基礎上，采用徑向基函數- 反向傳播神經網絡建立了具有良好泛化能力和預測精度的代理模型。利用改進的非支配排序遺傳算法對各炮口振動參數進行動力學優化，采用max-min準則從優化得到的Pareto最優解集中優選出一個較為兼顧各優化目標的解，與原模型結果對比，優化效果明顯。該方法能用于火炮多柔體動力學結構優化，也為火炮總體結構設計和相關優化提供了一定的參考。

兵器科學與技術；多柔體優化；炮口振動；徑向基函數- 反向傳播神經網絡；代理模型；遺傳算法

0 引言

多柔體系統動力學技術較多剛體理論考慮了身管等構件的柔性變形對結構動態響應的影響，廣泛應用在武器設計及其戰術指標優化中[1-2]。但隨著火炮現代化戰術要求和數值仿真精度技術要求的提高，現有的多柔體動力學技術在火炮結構優化等工程應用上面臨著更高的技術挑戰。

劉雷等[3]基于有限段思想建立了身管多體動力學模型，將身管離散為有限個剛性段，每兩段質心之間用一個無質量的梁連接，較精確地計算火炮的炮口擾動和描述身管的振動。劉林等[4]以某自行火炮火力部分作為研究對象，基于多體動力學和有限元方法，構建了考慮身管柔性化的火力部分剛柔耦合動力學模型。陳世業[5]提出了一種經由虛擬體組成的模擬身管來間接傳遞彈炮間相互作用力的方法，并以虛擬體為基礎建立了彈炮剛柔耦合多體系統模型。但縱觀現有文獻，有關于柔性體構件優化設計的卻很少，主要是工程應用層次的動力學系統中的柔體一般通過模態中性文件生成，用假設模態分析法來描述構件的振動變形，故很難像對剛體一樣直接進行參數化建模。

代理模型是設計優化中一種包含試驗設計和近似方法等多項內容的建模方法，它克服了工程優化中計算量過大的問題，在許多工程領域得到了廣泛的應用[6-8]。崔凱波等[9]用多剛體動力學計算炮口擾動，通過均勻試驗設計和徑向基函數(RBF)神經網絡建立炮口擾動和結構參數之間的非線性映射關系；梁傳健等[10]采用誤差反向傳播(BP)神經網絡和遺傳算法相結合的方法進行火炮結構動力學優化。但BP網絡學習速度慢、易陷入局部最優等不足，而RBF網絡具有學習快、能夠避免陷入局部最優等優點，但對訓練樣本依賴性強，泛化能力較差[11]。

研究的最終目的是為了指導工程實踐，本文對火炮的炮口振動響應進行多目標優化，從火炮結構方面盡量減少彈丸出炮口時的炮口起始擾動，提高火炮的射擊精度。但現有文獻[5,10,12]均采用設置權重系數將多目標問題轉化為單目標優化問題，這樣權重系數需人工預設，遺傳算法易出現早熟問題。

針對上述難點與不足，本文結合代理模型方法對火炮多柔體動力學模型進行結構優化。手動修改各構件的有限元網格，重新計算模態中性文件，以生成含不同柔性體結構的火炮動力學模型訓練樣本庫，并以此訓練近似模型。采用RBF-BP并聯組合神經網絡，它能克服RBF神經網絡和BP神經網絡的不足且同時具有兩者的優點，并運用遺傳算法獲得神經網絡的最佳初始權值和閾值。提出了基于精英策略非支配排序遺傳算法-II(NSGA-II)的多目標優化設計方法，進行火炮多柔體動力學結構優化研究。

1 火炮多體剛柔耦合動力學建模

1.1 柔性體構件的建立

工程應用層次的多體動力學分析時，其柔性體的創建一般是模態綜合法：先利用有限元軟件將各子構件離散成精細的網格，設置好邊界約束條件(界面節點)，進行模態計算生成模態中性文件；再在多體動力學計算軟件中導入模態中性文件建立柔性體，使用模態綜合法實現各柔性子構件與火炮多體動力學模型的耦合。

火炮系統中構件的運動屬于多自由度受迫振動，可用基于達朗貝爾原理的受迫振動方程來描述：

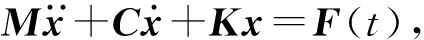
(1)

式中：M為質量矩陣；C為阻尼矩陣；K為剛度矩陣；F(t)為激勵力矩陣；x為位移矩陣；t為時間，表示激勵力是隨時間變化的。

使用模態分析法解此方程，可求得到物理坐標下的響應Q為

(2)

式中：矩陣A為系統振型進行正則化依次排列成；矩陣Z為系統的模態坐標。從(2)式可以看出，對于多自由度受迫振動系統，激勵的響應實際上是各階固有振型的線性疊加。模態坐標響應實際上表示了各階振型貢獻的大小，即模態貢獻因子。

根據模態貢獻因子理論，在實際工程運用中使用模態綜合法時只計算前幾階模態貢獻因子大的模態參數，而忽略其余階模態，可以在保證計算精度的同時大大減少計算時間。考慮到火炮系統發射問題的復雜性，選取前20階模態。

1.2 含多接觸的全炮剛柔耦合動力學建模

本算例以某大口徑牽引火炮為研究對象。基本假設：不考慮射擊過程中彈丸與身管的耦合作用，火炮發射前處于靜平衡狀態。

1.2.1 拓撲關系

全炮拓撲關系如圖1所示，導入對應部件的模態中性文件，分別創建身管、搖架(含高低機齒弧)及上架的柔性體，火炮其余部件均為剛體；分別建立該火炮各部件間及其與大地的連接關系，從而建立剛柔耦合多體動力學模型，圖2為該動力學模型的局部示意圖。全炮共有13個可動部件(含3個柔性體，不包括大地)，5個轉動約束和3個移動約束，11個固定約束，整個系統共133個自由度。

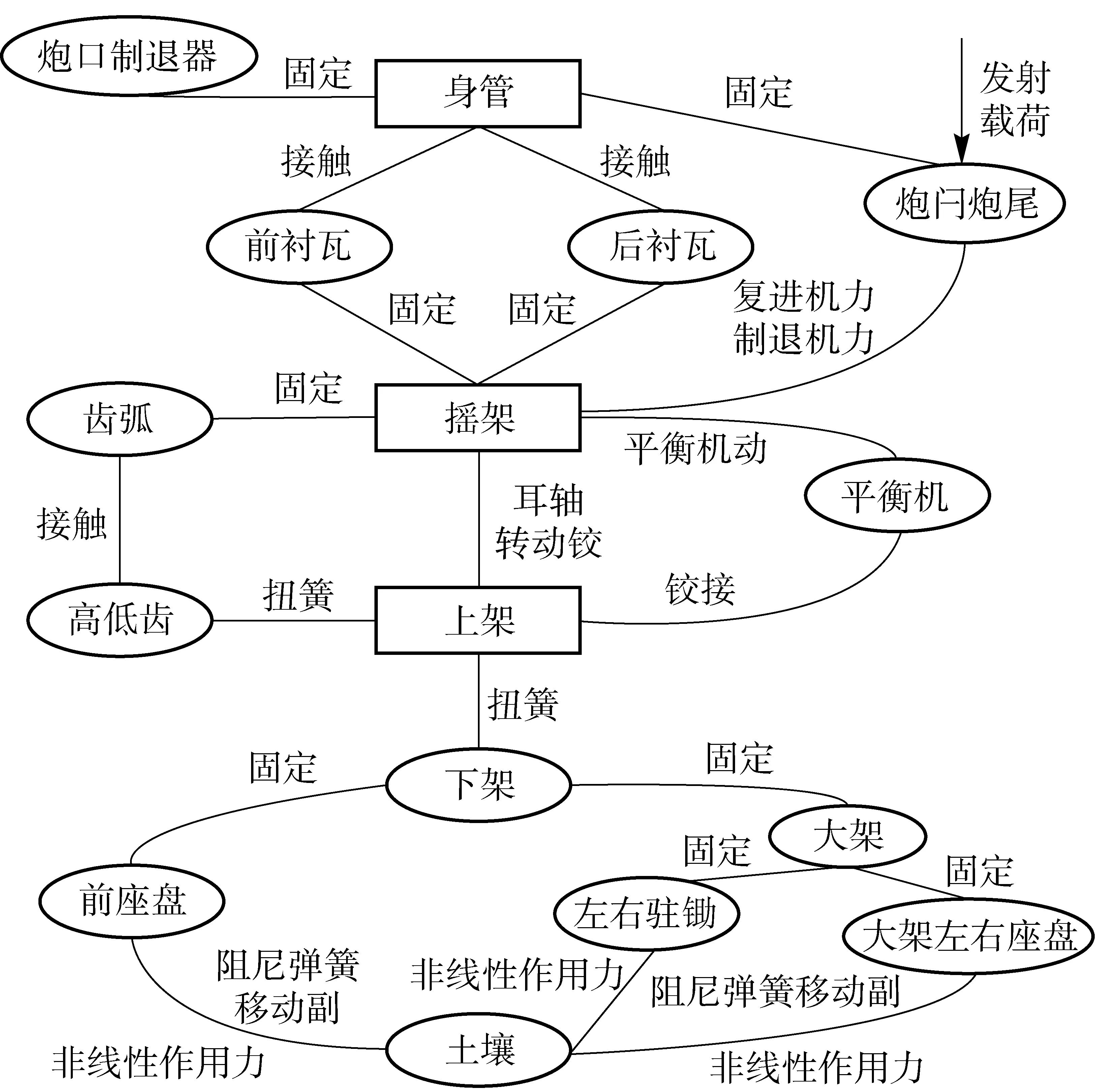
圖1 發射時全炮拓撲關系示意圖Fig.1 Topological structure of whole artillery during firing

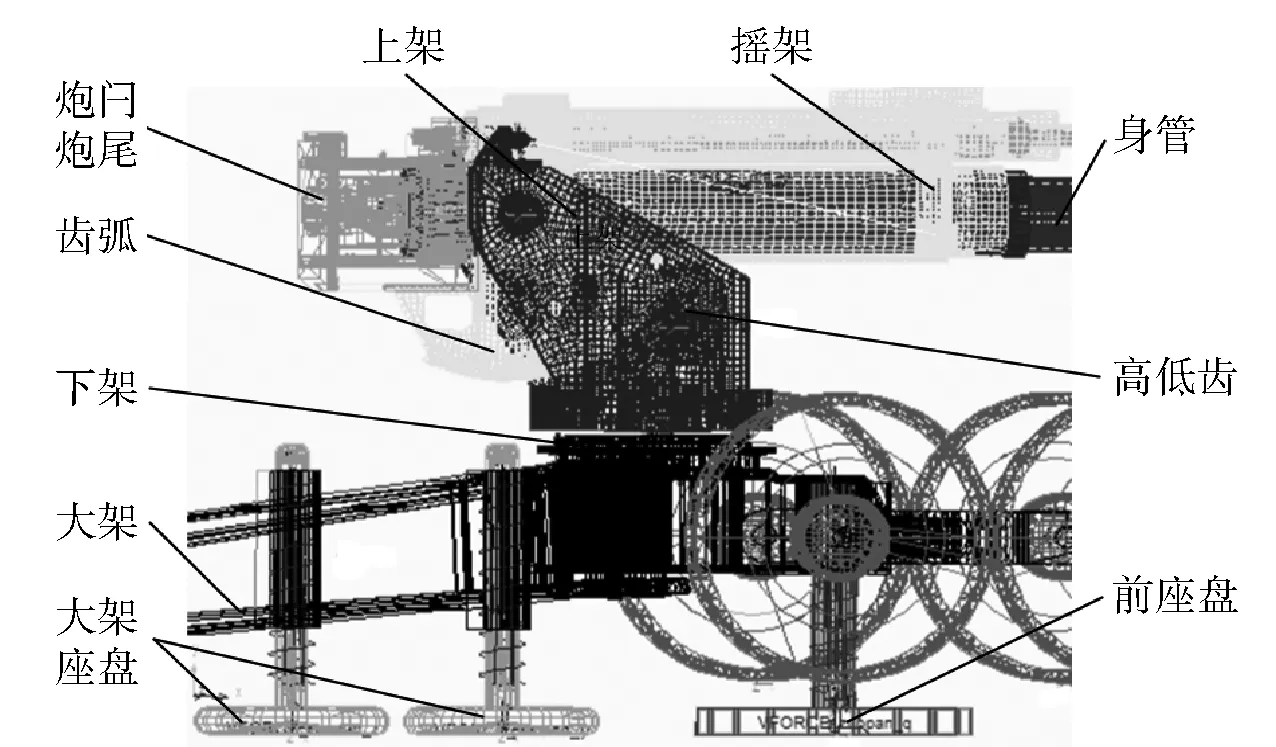
圖2 火炮剛柔耦合動力學模型局部圖Fig.2 Local diagram of artillery rigid-flexible coupling dynamics model

搖架前后襯瓦與身管、高低機齒弧和齒輪軸分別采用柔體- 柔體、柔體- 剛體接觸關系，其接觸碰撞參數獲取方法采用含微小間隙的改進接觸模型[13]計算得到；各彈性元件剛度和阻尼的獲取方法參考文獻[14]采用有限元分析的近似方法獲得；大架座盤、前座盤與土壤的作用力采用改進的Bekker非線性數學模型[15]計算得到。

炮膛合力、平衡機力、制退機力和復進機力是廣義坐標和廣義速度的函數，鑒于上述載荷計算函數比較復雜, 故使用ADAMS中提供的用戶自定義子程序模版(*.f)編程, 編譯鏈接生成動態鏈接庫(*.dll)，嵌入ADAMS動力學計算模型中，這些載荷均可根據后坐部分的后坐位移和后坐速度實時計算。

1.2.2 動力學方程

采用第一類拉格朗日方程建立系統動力學模型方程為

(3)

ψ(q,t)=0,

(4)

(5)

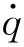
1.3 模型驗證

火炮發射時采用的工況：在中等硬度土壤地面上射擊，殺傷爆破榴彈、常溫、全裝藥，高低射角及方向射角均為0°. 將建好的全炮動力學模型進行數值仿真計算，并與實彈試驗測試結果進行對比，其對比結果見表1. 實彈試驗中，采用IDT公司生產的Y3-S2高速攝影設備采集發射過程火炮后坐運動的圖像信息，采用Xcitex公司的ProAnalyst軟件對捕獲的圖像進行分析，獲得后坐位移和速度試驗數據。利用后坐阻力計算公式計算后坐阻力；炮口角速度的測量采用的是七維航測科技公司的SDI-ARG-720型角速度陀螺傳感器測量，試驗中角速度陀螺儀布置在身管上距離炮口約370 mm處，數據采集系統選用的是DEWETRON 1201數據采集系統。由表1可以看出，數值計算結果與樣炮實測結果相對誤差很小，說明該動力學模型基本能夠反映該炮發射過程的實際情況，具有較好的可信度，可以作為代理模型樣本采集來源。

表1 數值計算結果與樣炮實測結果Tab.1 Simulated and test results

2 火炮多柔體動力學代理模型

2.1 代理模型參數選取

就火炮本身而言，表征炮口起始擾動的主要參量是彈丸出炮口瞬間炮口角位移、炮口角速度和速度，故以炮口中心處的各動態響應值為優化目標。為了有效減小炮口振動，設計變量應根據結構靈敏度分析的結果和實際工程經驗進行選取。本文在該火炮對應多剛體模型的靈敏度分析結果基礎上，考慮到火炮結構優化的可行性，結合參考文獻[9-10,12,16]和以往設計經驗進行設計變量的選取。選取后坐部分質量的垂向偏心距ey、橫向偏心距ez、耳軸中心處高度改變量Δhy這3個重要的總體結構參數及搖架前襯瓦軸向偏移量Δlx、搖架襯瓦與身管間隙量cb這兩個對炮口振動有重要影響的參數作為設計變量，其取值范圍根據以往火炮設計經驗選取。在此各設計變量的初值及取值范圍見表2.

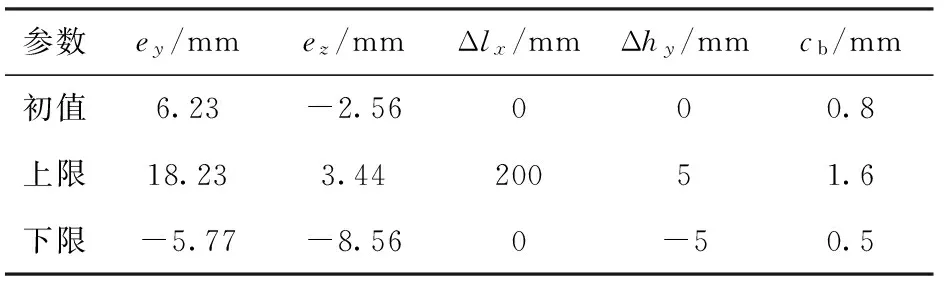
表2 各設計變量的初值及取值范圍Tab.2 Initial values and ranges of design variables

2.2 樣本庫建立

拉丁超立方設計是一種基于空間填充的實驗設計方法，它能夠使有限的樣本盡量填充整個設計空間，弱化了樣本邊界的要求，具有超強的非線性響應擬合能力等特點，更能實現對研究對象物理實質的體現。最優拉丁超立方設計通過外加一個準則大大改進了拉丁超立方設計的均勻性，使因子和響應的擬合更加精確、真實，特別適合用于多因素、多層次的試驗和系統模型完全未知的情況。

針對火炮發射動力學強非線性特性、設計變量和樣本的數量情況，本文選用最優拉丁超立方實驗設計獲取樣本點，共生成115組訓練樣本，部分樣本數據見表3.

分別根據表3設計變量取值修改多體剛柔耦合模型。具體說來，通過修改剛體炮閂炮尾的質量位置屬性來改變后坐部分偏心距參量值ey和ez；通過加長前襯瓦相連部分搖架前端長度并前移前襯瓦來改變前襯瓦偏移量Δlx；通過同時修改上架耳軸中心高度尺寸、搖架上耳軸中心位置高度來改變耳軸中心處高度改變量Δhy；通過同時修改襯瓦內徑和外徑值(保持厚度不變)，保持身管外徑不變，來改變搖架襯瓦與身管間隙量cb.

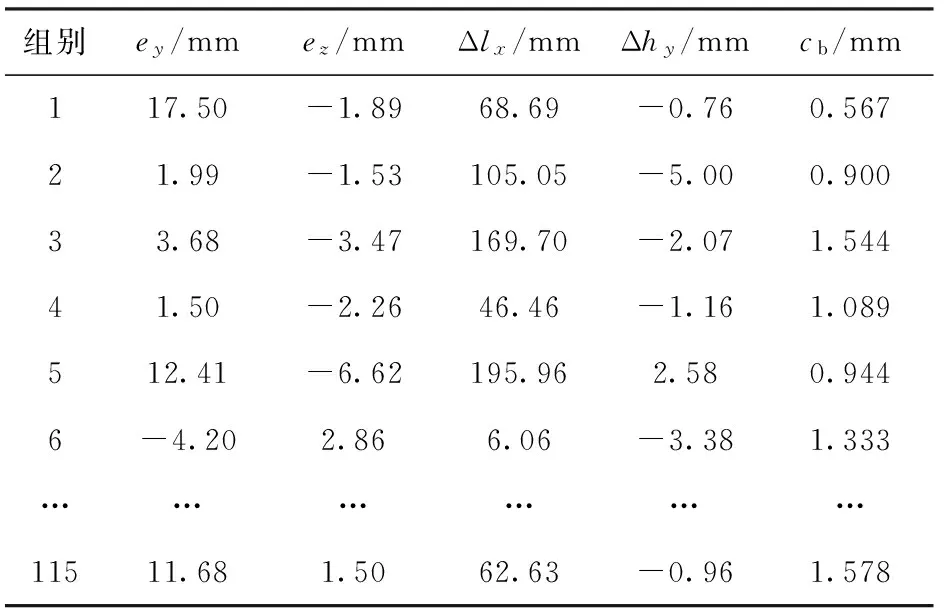
表3 訓練樣本數據Tab.3 Training sample data

柔性體部件的修改是先按樣本參數修改有限元網格模型，改變構件的尺寸和界面節點位置，并重新計算生成新的模態中性文件，再導入動力學模型替換原有部件。最后依次進行動力學仿真計算得到各樣本輸出值，樣本庫創建完畢。

2.3 RBF-BP并聯神經網絡的構建與遺傳優化

該RBF-BP并聯組合神經網絡是由一個RBF子網和一個BP子網兩部分并聯組合而成的雙隱藏層神經網絡，第1隱藏層結點的傳遞函數使用高斯函數，第2隱藏層結點的傳遞函數使用Sigmoid型函數。在該模型中，RBF子網絡使用高斯函數為徑向基函數，具體形式為

(6)

式中：X為l維輸入向量；ck為第k個徑向基函數的中心，與X具有相同的維數；σk為第k個隱含層神經元的徑向基函數寬度；‖X-ck‖2表示X～ck之間的歐幾里德范數，隨著它的增大，Ф(X)會逐漸衰減，直至為0，設隱含層神經元個數為K，則RBF子網絡的輸出為

(7)

w0為偏差，wk(k=1,2,…,K)為隱含層到輸出層的權值。

設BP子網絡的輸出為

Ok=f(netk),k=1,2,…,P,

(8)

則記RBF-BP神經網絡的輸出為

(9)

該RBF-BP并聯組合神經網絡結構采取的是5個輸入、4個輸出、2個隱含層的神經網絡，隱含層神經元的數目r與輸入層神經元的個數l有近似關系：r=2×l+1，因此這兩個隱含層的神經元個數均取11. 為了獲得更好的擬合精度(用復合相關指數R2評價)，采用試算法，每層神經元的個數從9到20逐個進行計算。試算發現，當兩個隱含層神經元均取15時，擬合精度最好，故隱含層神經元數均取15，共有154個權值和34個閾值。歸一化后的輸入樣本X先經過RBF神經網絡子網、BP神經網絡子網的輸入對其進行訓練，最后得到訓練結果。并且該網絡具有誤差反向學習的能力，當訓練結果達不到精度要求時，反向修改神經網絡的權值和閾值直至訓練結果達到精度要求，最后結束訓練。

另外，因無法準確獲得網絡的結構及初始連接權值和閾值，這對網絡訓練的影響很大。而遺傳算法具有較強的魯棒性，可以搜索全局的最優解，所以在對RBF-BP并聯神經網絡進行訓練時，采用與遺傳算法相結合的方式對網絡的權值和閾值進行優化，獲得最佳的初始權值和閾值，使優化后的神經網絡能夠更好地進行樣本診斷。編制Matlab程序實現上述RBF-BP并聯神經網絡的建模與優化。

圖3和圖4分別為使用隨機權值和閾值、使用優化后的權值和閾值兩種情況下的訓練誤差曲線。通過比較可以看出，遺傳算法優化初始權值和閾值前學習1 900次后均方誤差為0.000 75，未達到目標誤差(10-8)，而優化后的學習5次后均方誤差(1.558 7×10-9)已小于目標誤差，網絡訓練效果得到了很大的改善。

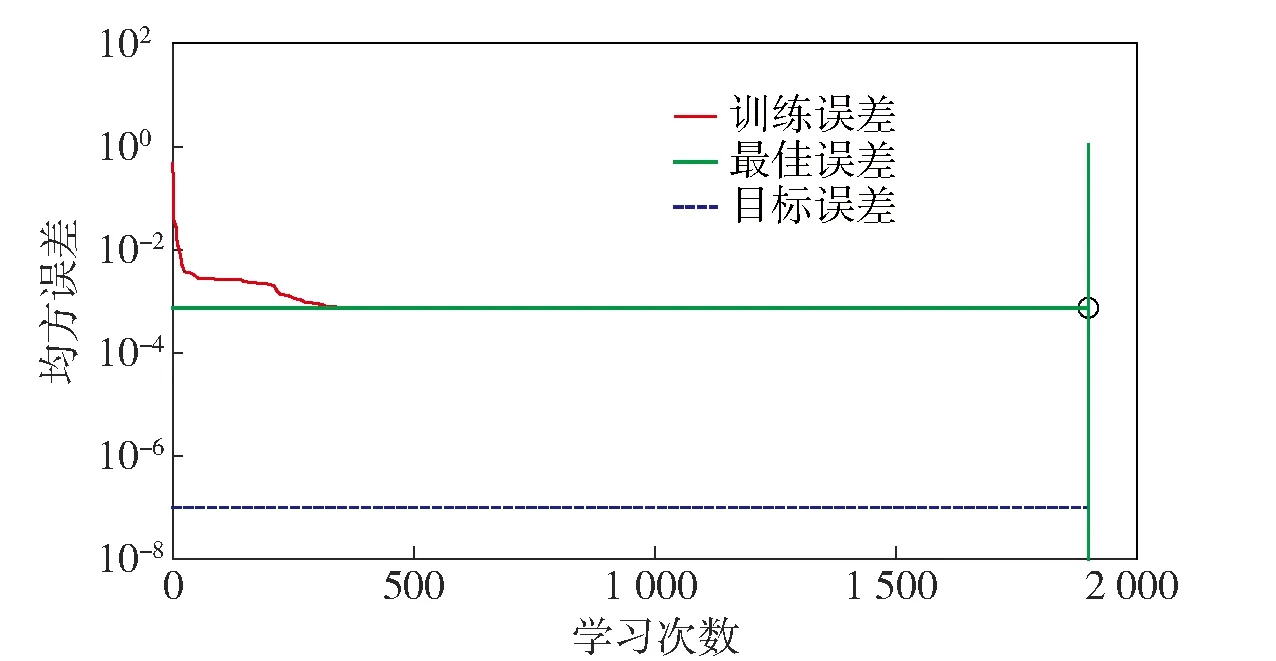
圖3 隨機權值和閾值訓練誤差曲線Fig.3 Training error curves for random weights and thresholds

圖4 優化權值和閾值后的訓練誤差曲線Fig.4 Training error curve after optimizing weights and thresholds

2.4 代理模型評價

代理模型構造后,必須經過有效的精度評價,保證模型的有效性，評價包括兩方面：樣本點的重現能力和非樣本點的預測能力。本文采用常用的復合相關指數R2進行測試評價。其表達式分別為

(10)

在實際基于代理模型的優化過程中,通常在設計空間隨機產生額外的測試點來評價代理模型精度。同樣根據最優拉丁超立方實驗設計在設計空間獲取30組測試樣本，依次計算出其響應值。將測試結果反歸一化后代入(10)式，可得檢測結果見表4.

表4 檢測結果Tab.4 Inspection results

根據表4檢測結果，復合相關指數均大于0.95，所建立近似模型具有良好的泛化能力和較高的預測精度。

3 火炮炮口振動的多目標優化

本算例待優化的目標值分別為炮彈出炮口瞬間炮口中心處的橫向角位移θy、高低角位移θz、高低角速度ωz，對應的目標函數分別為f1(x)、f2(x)和f3(x). 為了提高火炮射擊精度，它們的取值越小越好。該優化問題可以表述為

min [f1(x),f2(x),f3(x)]，
s.t.X∈∏(a,b),

(11)

式中：X、a和b分別為輸入參數及其下限、上限對應的數組，其取值范圍見表2.

適應度評估采用如(12)式所示的適應度函數：

(12)

式中：Fit(x)表示適應度函數；fi(x)為各目標函數；Ci,max為fi(x)的最大值估計，在此分別取訓練樣本中其最大值的絕對值，分別為0.024、0.054和28.274.

多目標優化問題最終得到的不是單一的解，而是許多解的集合，即Pareto前沿。為實現該多目標優化，引入了擁擠距離排序和精英保留機制的NSGA-II算法。該算法運算效率高，收斂性和魯棒性好。采用Matlab編制上述程序，參數設置：初始種群數選80，迭代次數為300，交叉效率為95%，變異概率0.2. 計算得到Pareto前沿如圖5所示。

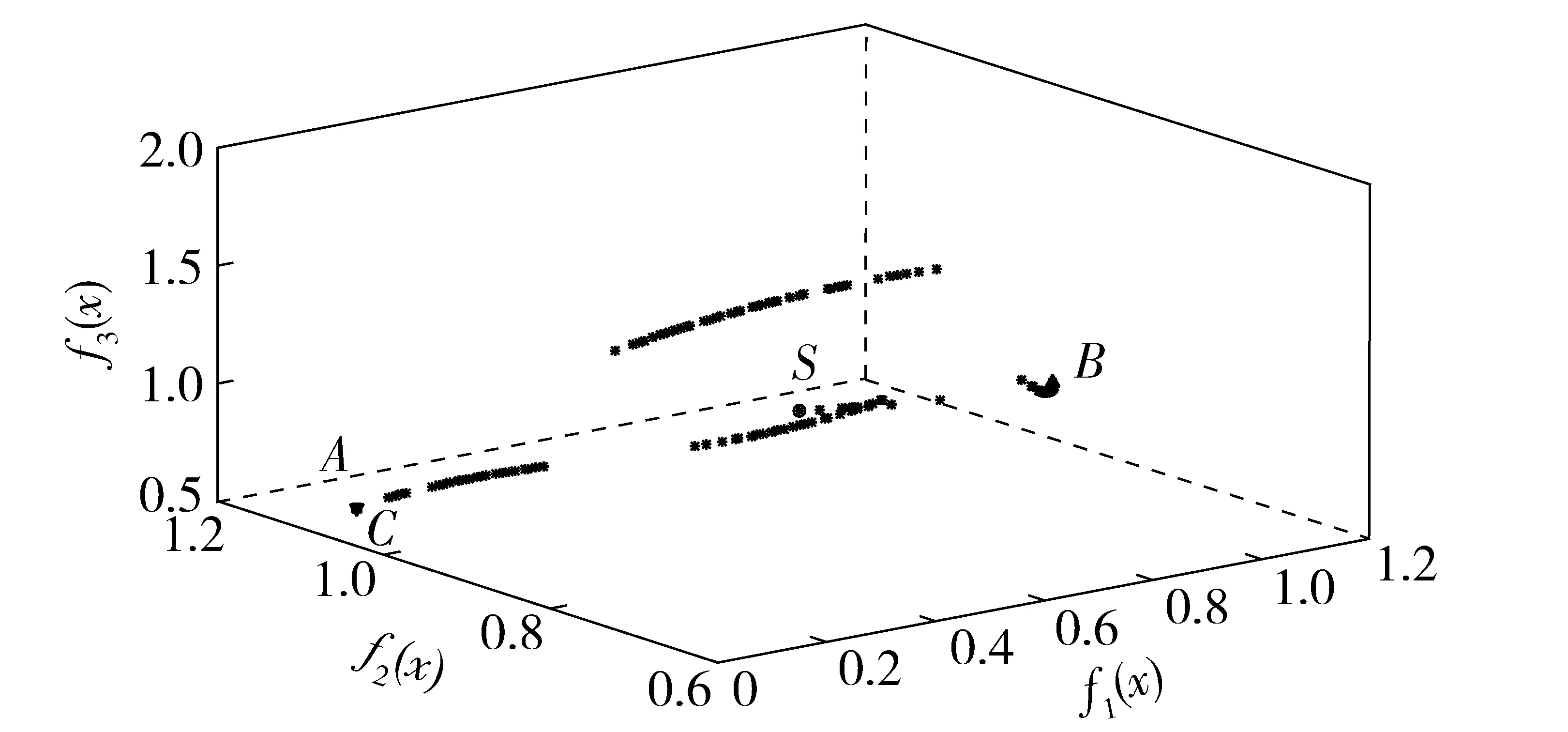
圖5 優化所得Pareto前沿Fig.5 Optimized Pareto front

為了選擇一個兼顧多個目標的解，本文依據max-min準則[17]進行優選，其表達式如(13)式所示。選出一個可行解如圖5中S標記點所示。

(13)

在通常情況下這3個優化目標是相互矛盾的，一個解可能在某個目標上最優，但在其他目標上則可能很差。圖5中A、B和C3點所指解分別為f1、f2和f3的單方向最優解，但是此時其他兩個目標值不是很好。A、B、C和S4個可行解對應的設計變量和優化目標值見表5. 需要指出的是，這些方案間沒有優劣之分，設計者可根據實際需求進行方案選取。

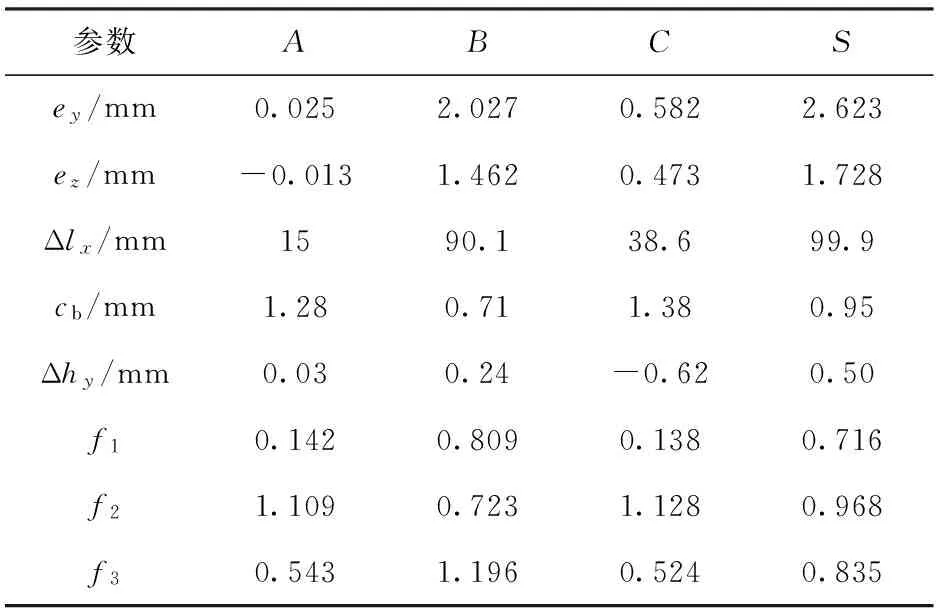
表5 A、B、C和S 4個可行解對應參數值Tab.5 Parameter values associated to the solutionsA, B, C and S

按經優化、優選出來S方案中的設計變量值構建ADAMS多柔體火炮發射動力學模型進行數值仿真計算，所得結果與代理模型結果、原始模型仿真結果對比見表6.

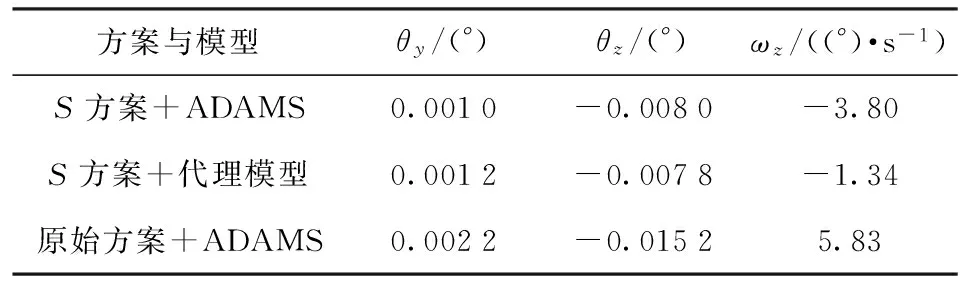
表6 優化優選后結果對比Tab.6 Result comparison

由此可以看出，S方案在代理模型和ADAMS仿真計算結果有一些出入，這與代理模型的近似精度有關，考慮到火炮射擊動力學過程的復雜性，這些出入均在可接受范圍之類。

圖6為S方案和原始方案3個優化目標的對比曲線圖。由于本文采用的神經網絡代理模型僅能表征設計變量與彈丸出炮口瞬間炮口中心處的炮口角位移和角速度之間的映射關系，故在圖6各圖中代理模型下S方案的值僅只有一個離散點。結合表6，可以看出優化后，出炮口瞬間，炮口中心處的橫向角位移θy、高低角位移θz分別減少了約50%和47%，高低角速度ωz的絕對值也減少了35%，符號不同僅表示速度的方向不同。且在整個膛內時期這3個優化目標的幅值均變小了，曲線變化趨勢更加平緩。

圖6 優化方案與原方案優化結果對比Fig.6 Optimized results of original and optimized schemes

4 結論

針對火炮結構動力學優化時柔性體模態文件不易直接參數化、很難進行結構優化等問題，本文提出一種結合代理模型的優化方法，并以某火炮炮口動態響應多目標優化問題為算例進行了驗證。

1)將多學科代理模型方法引入火炮動力學建模。針對多柔體動力學模型很難直接參數化建模優化的問題，提出綜合運用多體系統剛柔耦合動力學、最優拉丁超立方實驗設計、遺傳算法和RBF-BP人工神經網絡等方法建立火炮發射動力學代理模型的思路，為后續火炮結構動力學優化提供了較為便捷的基礎。

2)RBF-BP組合神經網絡彌補了RBP神經網絡和BP神經網絡各自的缺點，并具有其雙方優點，適合用于具有強非線性的火炮發射動力學問題近似建模。運用遺傳算法優化神經網絡的權值和閾值使優化后的神經網絡能夠更好地進行樣本預測。

3)基于NSGA-II的多目標優化設計方法可以同時對炮口多個動態響應目標函數進行優化設計，能夠輸出一組備選方案(Pareto解集)，設計者可以從中選取滿足不同需求的特殊解，對實際炮口振動優化設計有一定的參考價值。另外，采用Max-min準則，可以快速從Pareto解集中優選出一個兼顧各個目標的方案。

References)

[1] Sneck H J. Main battle tank flexible gun tube disturbance model: three-segment mode[C]∥10th US Army Gun Dynamics Symposium. Austin, TX, US:University of Texas, 2002: 92-106.

[2] Rui X T，Rong B，Wang G P，et al. Discrete time transfer matrix method for dynamics analysis of complex weapon systems[J]. Science China Technological Sciences, 2011, 54(5): 1061-1071.

[3] 劉雷,陳運生. 身管多體動力學模型研究[J]. 南京理工大學學報, 2005, 29(3): 267-269,295-296. LIU Lei, CHEN Yun-sheng. Multi-body dynamic model of barrel[J]. Journal of Nanjing University of Science and Technology, 2005, 29(3): 267-269,295-296. (in Chinese)

[4] 劉林,狄長春,李云峰，等. 身管柔性化對火炮動力后坐試驗的影響研究[J]. 軍械工程學院學報，2011, 23(1): 31-34. LIU Lin, DI Chang-chun, LI Yun-feng, et al. Research on dynamic recoil test of gun with flexible gun barrel[J]. Journal of Ordnance Engineering College, 2011, 23(1): 31-34. (in Chinese)

[5] 陳世業. 自行火炮彈炮多體發射系統動力學仿真研究[D]. 南京：南京理工大學, 2013. CHEN Shi-ye. Dynamics simulation for the projectile-barrel multi-body launching system of the self-propelled artillery[D]. Nanjing: Nanjing University of Science and Technology, 2013. (in Chinese)

[6] Kleijnen, J P. Kriging metamodeling in simulation:a review[J]. European Journal of Operational Research, 2009, 192(3): 707-716.

[7] 陳國棟. 基于代理模型的多目標優化方法及其在車身設計中的應用[D].長沙：湖南大學, 2012. CHEN Guo-dong. Multi-objective optimization method based on metamodel and its applications in vehicle body design[D]. Changsha: Hunan University, 2012. (in Chinese)

[8] 龍騰,郭曉松,彭磊,等. 基于信賴域的動態徑向基函數代理模型優化策略[J]. 機械工程學報, 2014, 50(7)：184-190. LONG Teng, GUO Xiao-song, PENG Lei, et al. Optimization strategy using dynamic radial basis function metamodel based on trust region[J]. Journal of Mechanical Engineering, 2014, 50(7): 184-190. (in Chinese)

[9] 崔凱波,秦俊奇,狄長春,等. 基于均勻設計與RBF網絡的火炮優化目標函數構建方法研究[J]. 機械設計, 2013, 30(2): 45-48. CUI Kai-bo, QIN Jun-qi, DI Chang-chun, et al. Research on establishment measures of artillery objective function by uniform design method and RBF network[J]. Journal of Machine Design, 2013, 30(2): 45-48. (in Chinese)

[10] 梁傳建,楊國來,王曉鋒. 基于神經網絡和遺傳算法的火炮結構動力學優化[J]. 兵工學報，2015，36(5)：789-794. LIANG Chuan-jian, YANG Guo-lai, WANG Xiao-feng. Structural dynamics optimization of gun based on neural networks and genetic algorithms[J]. Acta Armamentarii, 2015, 36(5): 789-794. (in Chinese)

[11] K?kkülünk G, Akdoan E, Ayhan V. Prediction of emissions and exhaust temperature for direct injection diesel engine with emulsified fuel using ANN[J]. Turkish Journal of Electrical Engineering and Computer Sciences, 2013, 21(2):2141-2152.

[12] 周樂,楊國來,葛建立,等. 基于遺傳算法的火炮反后坐裝置結構多目標優化研究[J]. 兵工學報，2015，36(3)：433-436. ZHOU Le,YANG Guo-lai,GE Jian-li, et al. Structural multi-objective optimization of artillery recoil mechanism based on genetic algorithm[J]. Acta Armamentarii,2015,36(3):433-436.(in Chinese)

[13] 蕭輝,楊國來,葛建立,等. 反后坐裝置布局對炮口振動的影響研究[J]. 彈道學報, 2016, 28(2): 53-56，86. XIAO Hui, YANG Guo-lai, GE Jian-li, et al. Research on influence of recoil mechanism structure on muzzle disturbance[J]. Journal of Ballistics, 2016, 28(2): 53-56，86. (in Chinese)

[14] 劉雷. 自行火炮剛彈耦合發射動力學[D].南京:南京理工大學, 2005. LIU Lei. Self-propelled guns rigid-flexible coupling launch dynamics[D]. Nanjing: Nanjing University of Science and Technology, 2005. (in Chinese)

[15] 楊國來,陳運生. 考慮土壤特性的車載榴彈炮射擊穩定性研究[J]. 南京理工大學學報:自然科學版, 2006, 30(4): 495-498. YANG Guo-lai, CHEN Yun-sheng. Investigation on firing stability of vehicle mounted howitzer with consideration of soil property[J]. Journal of Nanjing University of Science and Technology, 2006, 30(4): 495-498. (in Chinese)

[16] 張俊飛. 某火炮結構參數靈敏度分析與優化研究[D].南京：南京理工大學, 2014. ZHANG Jun-fei. Research on sensitivity analysis and structal optimization of a towed howitzer[D]. Nanjing: Nanjing University of Science and Technology, 2014. (in Chinese)

Research on Flexible Multi-body Dynamics Structure Optimization of Artilleries

XIAO Hui, YANG Guo-lai, SUN Quan-zhao

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)

In allusion to the problem of that the existing structural dynamics optimization methods cannot optimize the flexible parts in flexible multi-body dynamic systems, a method combining multidisciplinary agent models and the improved nondominated sorting genetic algorithm (NSGA-II) is proposed. Based on an experimentally authenticated rigid-flexible coupled multibody model, a surrogate model with good generalization ability and forecasting accuracy is established with RBF-BP neural network. In the proposed model, the muzzle vibration parameters are used as outputs, and the modal parameters of flexible part and some general structural parameters are taken as inputs. Nondominated sorting genetic algorithm is used to improve the muzzle vibration characteristics, and the max-min criterion is adopted to select a solution from the Pareto front. The optimized effect is compared with the optimized result of the original model. The result shows that the proposed method can be used for optimization of artillery flexible multi-body dynamics structure.

ordnance science and technology; flexible multi-body optimization; muzzle vibration; RBF-BP neural network; surrogate model; genetic algorithm

2016-06-02

國家自然科學基金項目(11572158)；國家“973”計劃項目(1503613249)

蕭輝 (1988—), 男, 博士研究生。E-mail: xiaohui238@gmail.com

楊國來(1968—), 男, 教授，博士生導師。E-mail: yyanggl@mail.njust.edu.com

TJ302

A

1000-1093(2017)01-0027-08

10.3969/j.issn.1000-1093.2017.01.004