波箔氣體軸承溫度場計算與動靜態性能分析

李長林， 杜建軍， 姚英學

(哈爾濱工業大學深圳研究生院 機電工程與自動化學院， 廣東 深圳 518055)

?

波箔氣體軸承溫度場計算與動靜態性能分析

李長林， 杜建軍， 姚英學

(哈爾濱工業大學深圳研究生院 機電工程與自動化學院， 廣東 深圳 518055)

為計算波箔軸承的溫度場分布，研究軸承的熱特性，推導了考慮外部冷卻條件時的平箔片內表面等效對流換熱系數，將箔片一側的導熱換熱模型耦合到氣膜三維能量傳遞模型中.建立軸承套、轉子的導熱與對流換熱模型，耦合求解非等溫Reynolds方程、氣膜能量傳遞方程、箔片變形方程.計算并分析軸承轉速、載荷、外部冷卻氣流等因素對軸承溫度的影響，分析了軸承的靜動態性能.結果表明: 轉速對軸承溫度影響很大，溫度隨載荷變化不大，冷卻空氣的冷卻效率隨流量增大逐漸降低.與等溫條件相比，非等溫模型的軸承承載能力較大，且具有較大的動態剛度與阻尼.

波箔氣體動壓軸承；溫度場；流體熱動力模型；能量傳遞方程；多場耦合

波箔氣體動壓軸承最早出現在上個世紀60年代，在之后的幾十年間，理論與實驗研究都獲得了較快的發展[1-2]，軸承的承載能力與穩定性都隨著箔片結構的改進與涂層技術的發展獲得了較大的提高[3].近十幾年來，波箔軸承開始逐漸被應用在一些極限環境中，例如，微型燃氣輪機、汽車渦輪增壓器、透平膨脹機、空氣壓縮機、鼓風機等[4-6].即使波箔氣體軸承比傳統的液體軸承與滾珠軸承對高溫環境有更好的適應性，但是在高轉速與高溫環境中，如果缺乏充分的溫度控制，軸承性能會受到較大影響[7-8].

波箔氣體軸承熱特性的理論與實驗研究一直比較匱乏，Salehi等[9]通過Couette近似，忽略了氣膜壓力梯度對于能量方程的影響，而將能量方程與雷諾方程解耦，單獨求解了波箔軸承一維溫度分布，但其建立的模型比較簡單，并沒有建立箔片結構與轉子的熱模型.Peng等[10]采用有限差分法對能量方程離散處理，在平箔片外表面采用等效對流換熱系數模擬了箔片一側的邊界條件，求得了氣膜三維溫度分布，但是作者忽略了箔片結構的導熱與換熱，也沒有給出明確的轉子溫度邊界條件.Lee等[11]建立了更加完整與復雜的軸承熱傳遞模型，考慮了波箔冷卻通道的對流換熱以及轉子的軸向導熱，給出了相對充分的熱邊界條件.Feng等[12]推導了箔片一側的等效對流換熱系數，同時轉子內通冷卻氣進行冷卻.氣膜徑向方向采用稀疏網格建模，用Lobatto點積分來表示稀疏網格上的值，縮小了計算量，理論計算結果與之前的實驗結果比較接近，但是作者簡化了箔片結構來建立熱模型，與實際情況有所出入.Andrés 等[13]介紹了用二維 THD 模型來研究波箔軸承的熱特性.該模型研究了軸承內熱量的產生于向周圍環境的傳遞過程，推導出了可以簡化計算的等效對流換熱系數，但文中作者通過對三維能量方程沿著氣膜厚度對溫度積分的方法的準確性沒有得到驗證.Salehi等[9]也進行了實驗研究，在波箔通道中通入冷卻氣體，表明有80%熱量流入外冷卻通道中.Dellacorte[14]搭建了一個波箔軸承在高溫環境下運行的實驗臺，試驗臺能夠提供最高7×104r/min的軸承轉速與700 ℃的軸承工作環境.Radil等[15]針對第三代波箔軸承熱特性進行了實驗研究，在不同載荷分布(9～222 N)，不同轉速條件(2.0×104～5.0×104r/min)下，測量了氣膜溫度沿圓周方向與軸向方向的分布情況.

本文考慮實際的箔片結構與冷卻條件，建立了較復雜的波箔軸承能量傳遞模型，設立了完整的熱邊界條件，與實際熱流狀態非常接近.數值耦合求解了氣膜三維能量傳遞方程、能量方程與氣膜厚度方程，有效地避免了之前理論研究模型的不足之處.

1 理論模型

波箔氣體動壓軸承主要包括：用于形成潤滑表面的平箔片，起彈性支撐作用的波形箔片，軸承套與轉子.軸承主要結構如圖1所示.

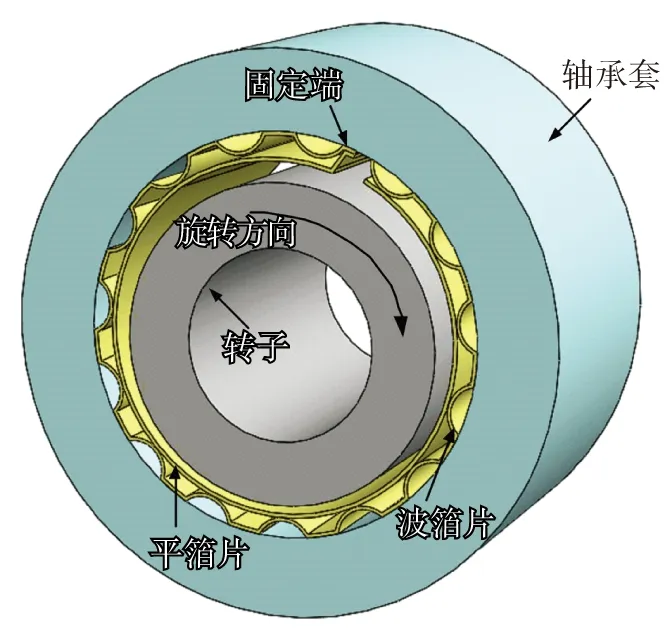
圖1 波箔軸承結構示意

軸承高速運行時，微米級的氣膜厚度使氣體分子間摩擦生熱嚴重，較小的空氣比熱容使熱量很難傳遞出去，因此會導致較大溫升.軸承內部熱量傳遞方式與傳遞通道如圖2所示.熱量在氣膜內部產生，一部分流向箔片結構，一部分通過軸承端部排出的氣體傳出，另一部分通過轉子流到周圍環境中.

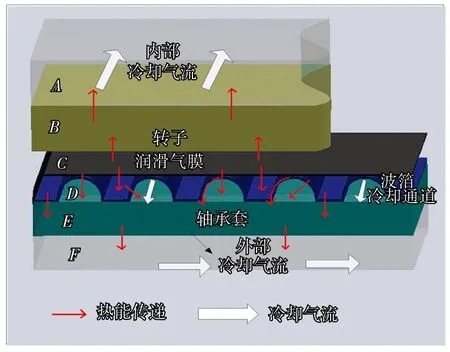
圖2 軸承系統能量傳遞模型

1.1 潤滑氣膜流體熱動力模型

氣膜內部的氣體流動狀態可以用Reynolds控制方程表征.非等溫條件下，穩態Reynolds方程為

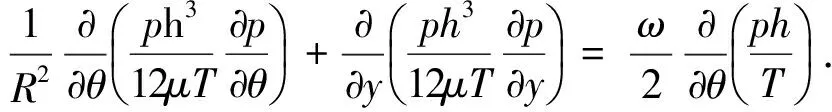
(1)

式中：μ為氣體黏度(Pa·s)；T為氣膜溫度(K)； x為圓周方向，x=R·θ；y為軸承寬度方向；z為氣膜厚度方向；ω為轉子角速度(rad/s).氣體的黏度與溫度存在一定關系：

μ=a(T-Tref).

式中: a=4×10-8，Tref=-185.59 K.

氣膜的能量傳遞是由三維能量傳遞控制方程描述的，由于圓周方向氣體流速很大，因此沿圓周方向的導熱量與對流換熱量相比非常小，可以忽略.同時由于氣膜很薄，氣膜厚度方向的氣體流速較小，則氣膜厚度方向的熱傳導是主要的熱傳遞形式，因此z方向的對流換熱可以忽略.簡化后的能量方程為

(2)

式中：cp為氣體定壓比熱容(J/(kg·K))，k為氣體導熱系數(W/(m·K))，u為氣膜圓周方向速度(m/s)，v為氣膜軸向方向速度(m/s).

箔片結構的變形，高轉速條件下轉子的熱膨脹與離心膨脹，箔片結構熱膨脹都會相應地改變氣膜厚度分布.因此，非等溫條件下，波箔軸承的氣膜厚度可以表示為

h=c(1+εcos φ)+(p-pa)·s/kb-δgc-ΔCt.

(3)

式中：c為初始氣膜間隙(m)；s為波箔節距(m)；kb為單位軸向波箔長度剛度(N/m2)；δgc為轉子離心膨脹(m)；ΔCt為軸承系統熱膨脹(m)，ΔCt=δs+δf-δh；δs為轉子外表面的熱膨脹；δf為箔片結構的熱膨脹；δh為軸承套內表面的熱膨脹.

δgc為轉子的離心膨脹，且

δgc=ρsRω2/(4Es)[R2(1-ν)+Rin2(3+ν)].

式中：ρs為轉子密度, R為轉子外表面半徑, ω為軸承轉速(rad/s), v為轉子材料泊松比, Rin為空心轉子內表面半徑, Es為轉子的彈性模量.

氣膜能量方程的邊界條件為

T|z=0=TR,

T|θ=0=Tinlet,

T|z=1=Ttop.

式中：TR為轉子表面溫度(K), Tinlet為平箔片前端入口氣膜溫度(K), Ttop為平箔片表面溫度(K).

因此氣膜能量傳遞模型與轉子熱傳遞模型、箔片一側導熱換熱模型、平箔片前端氣體混合模型之間有緊密的聯系.轉子外表面與平箔片內表面都和潤滑氣膜接觸，因此接觸表面上兩個模型的對應點具有相同的溫度，在整個接觸面滿足熱流平衡條件.同時，平箔片前端混合模型的輸出值是氣膜能量傳遞模型的輸入值.

能量方程與Reynolds方程都是非線性二階偏微分方程，不能夠直接求解，采用有限差分法進行離散求解能夠獲得較高精度解.從式(1)～(3)中可以看出，氣膜能量方程、非等溫Reynolds方程、氣膜厚度方程之間是相互耦合的，需要通過迭代的方式得到3個方程的收斂解.

1.2 箔片結構一側的導熱換熱模型

氣膜內部產生的熱量一部分向箔片結構傳遞，如果波箔通道中通入冷卻氣，那么熱流流經平箔片后，大部分通過對流換熱的方式由平箔片傳到冷卻氣流中，一部分通過熱傳導流經波箔片與軸承套，經自然對流換熱傳到環境空氣中.同時，熱流也會由波箔表面與軸承套內表面傳到冷卻空氣中，具體能量傳遞示意圖如圖3所示.

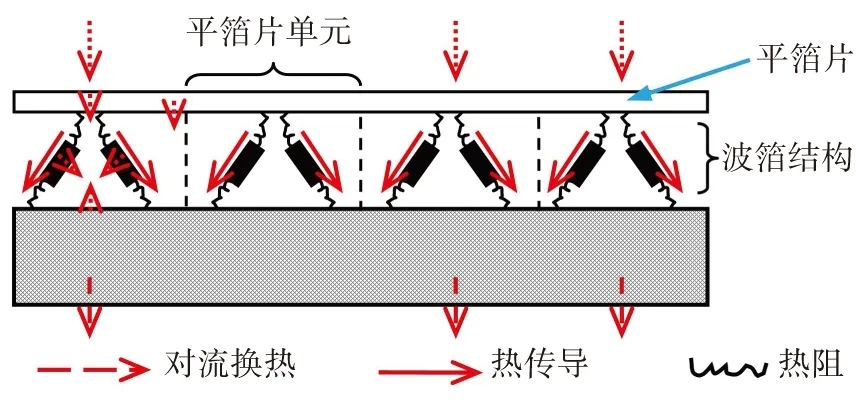
圖3 箔片結構熱流傳遞示意圖

由氣膜內部熱量向平箔片傳遞的總熱量可以分為3個部分，參照圖2，通過能量守恒可得

Qfilm→foil=QC→cooling+QD→cooling+QE→F.

式中：C為平箔外表面(遠離轉子一側)，D為波箔片，E為軸承套外表面，F為環境空氣.

由熱流傳遞的連續性與能量守恒條件，可以推導出平箔片內表面(靠近轉子一側)的等效對流換熱系數.氣膜與平箔片內表面相接觸，邊界溫度條件就可以表示為

(4)

式中：

N=hconv_tAtop+0.5M×hconv_tAtopRtop_bump+M-hconv_hAbhA×Rbump_h/Rtop_bump，

M=hconv_bAbump+0.5hconv_hAbhAhconv_bAbumpRbump_h+hconv_hAbhA+hconv_hAbhA×Rbump_h/Rtop_bump，

M0=hconv_bAbump+0.5hconv_hAbhAhconv_bAbumpRbump_h+hconv_hAbhA，

N0=M0+hconv_tAtop+0.5M×hconv_tAtopRtop_bump.

式中：ka為氣膜導熱系數， Atop為平箔片單元面積，tf為平箔片厚度，Rtop_bump為平箔片與波箔片的接觸熱阻[11]，hconv_t為平箔片外表面的對流換熱系數，hconv_b為波箔表面的強迫對流換熱系數，hconv_h為軸承套外表面的自然對流換熱系數[16]，Rbump_h為波箔片與軸承套之間的接觸熱阻[11].

推導得到的等效對流換熱系數γ包括了與外部冷卻條件與箔片結構特征有關的參數，并通過式(4)將復雜的箔片結構熱模型歸并到能量方程的一個邊界條件上.

1.3 平箔片前端氣體混合模型

由于軸承結構的特殊性，氣膜內部不會有低于大氣壓的情況，軸承端部排出的氣體從平箔片前端補充，保證氣膜間隙的氣體質量守恒.補充進來的常溫氣體與循環高溫氣體混合達到一定冷卻效果.基于熱循環氣流與進氣冷卻氣流與混合氣流的能量守恒條件，因此在平箔片前端的溫度邊界條件為

Tin=(Trecqrec+Tsucqsuc)/(qrec+qsuc).

式中：Tin為平箔片前端的混合入口溫度，Trec為平箔片后沿的循環氣流溫度，Tsuc為吸入冷卻空氣的溫度，為室溫T0；qrec為循環氣流量，qsuc為吸入的冷卻氣體的流量.

計算得到的入口氣膜溫度Tin作為氣膜能量方程的一個邊界條件，帶入到能量方程中進行求解，在圓周方向以向后差分的形式可以迭代求解循環溫度值Trec，并將Trec作為氣體混合模型的輸入值，計算得到新的入口氣膜溫度Tin，完成一個耦合迭代過程.

1.4 轉子熱傳遞模型

氣膜內部產生的熱量一部分傳向轉子，經轉子孔壁傳到內表面，經對流換熱傳出.在這個過程中滿足能量傳遞的連續性，由氣膜傳向轉子的熱流Qfilm→rotor與轉子內表面換熱量Qrotor_inner→cooling分別為

式中：k為氣膜導熱系數，h為氣膜厚度；L為軸承寬度，kcond_s為轉子導熱系數，Rin為轉子內半徑.

在模型耦合求解時，先給定較低的轉子表面溫度，以此作為邊界條件計算氣膜三維溫度分布，同時可以得到轉子的一維徑向溫度分布，則轉子內外表面的總熱流量可分別計算得到，將內外表面的熱流差值作為總體迭代過程的收斂特征.

1.5 動態剛度與阻尼求解

通過小擾動法數值求解非等溫條件下的動態Reynolds方程

可以計算出軸承的動態剛度與阻尼系數.在轉子的平衡位置產生的微擾動位移模式為

ΔX=Δx/C=|ΔX|eivt，ΔY=Δy/C=|ΔY|eivt.

其中:v為渦動頻率;γ為v與轉子角速度ω的比值，簡稱渦動比，γ=v/ω.當轉子受到外界擾動時，動態載荷也可以在平衡位置基于擾動位移與擾動速度按照泰勒公式展開：

則動態剛度與阻尼系數可以定義為

2 計算結果與分析

2.1 結果驗證

為了證明理論模型與編程的正確性，將計算結果與文獻[15]中的實驗結果進行對比，文獻[15]中的軸承的結構參數、運行參數與氣體屬性參數見表1、2.

表1 計算初始參數

表2 波箔軸承結構參數

2.2 程序計算流程圖

程序計算流程圖如圖4所示，先進行等溫條件下氣彈耦合解，并根據計算的氣膜壓力、厚度通過能量方程計算氣膜溫度分布，根據計算的氣膜溫度更新氣膜厚度與軸承結構特性參數、氣膜特性參數，并在此基礎上求解非等溫條件下的Reynolds方程.按照這種迭代求解方式，最終能夠得到收斂的氣膜壓力、氣膜厚度分布與氣膜溫度分布.

2.3 程序驗證

采用表1、2中的初始參數，計算軸承轉速為2.0×104～5.0×104r/min，不同載荷條件下的軸承峰值溫度，理論計算值與文獻中的實驗數據對比結果如圖5所示.

從圖5中可以看出，理論計算結果與文獻數據有一定差距，實驗數據的氣膜峰值溫度更容易受軸承載荷的影響，理論結果的氣膜峰值溫度隨著載荷增加也有一定程度的增加，但變化趨勢不明顯.理論與實驗結果都反應出軸承轉速是影響氣膜溫度的主要因素，不同轉速時，理論計算結果的溫度值與實驗數據接近，一定程度上驗證了模型的準確性.

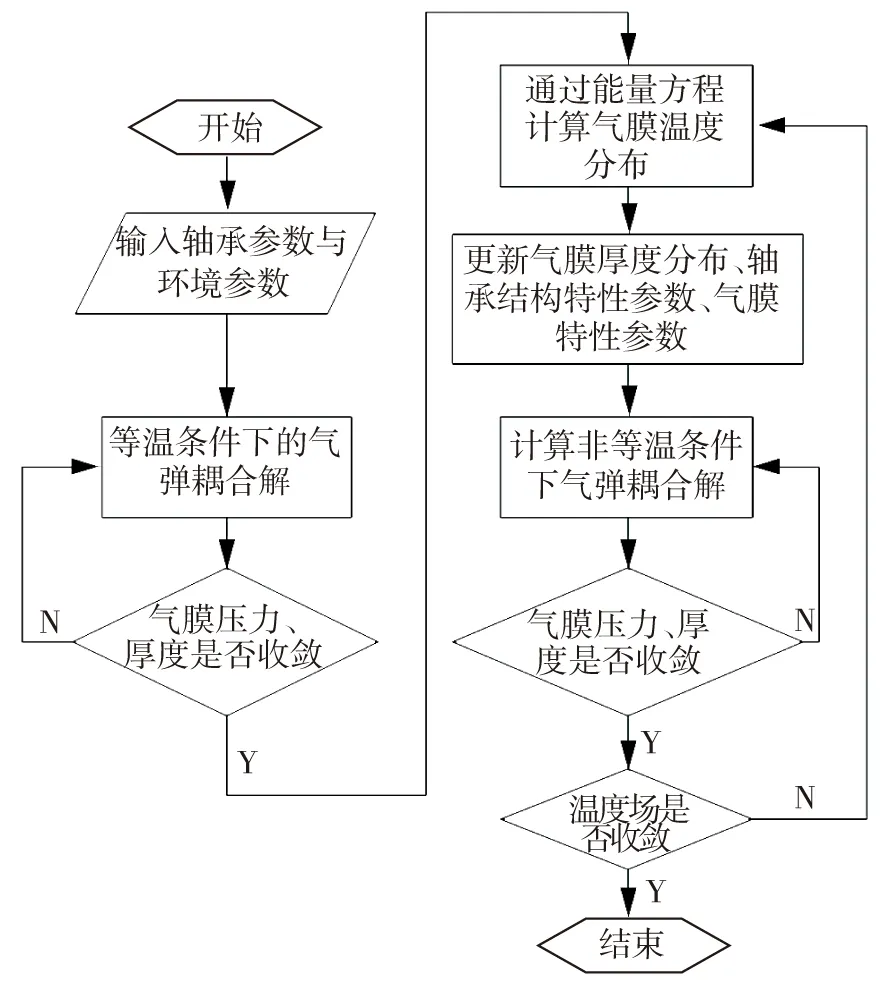
圖4 程序計算流程圖

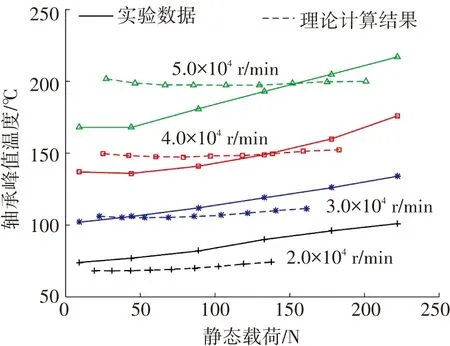
圖5 不同轉速與載荷下氣膜峰值溫度計算值與文獻[15]對比 Fig.5 Theoretical and experimental peak film temperatures under different bearing load and speed conditions

2.4 軸承溫度的影響因素分析

從圖5中可看出，轉速變化對軸承溫度有較大影響，載荷變化的影響較小.圖6為相同載荷、不同轉速條件下，外部冷卻氣流對軸承溫度的影響情況.從圖6中可看出，外部冷卻氣流對軸承溫度有較大的影響.當冷卻氣流流量從0增大到0.2 m3/min時，軸承峰值溫度下降了1半.但同時也可以發現，冷卻氣流的冷卻效率隨著流量的增大逐漸降低.

圖7描述了相同載荷、不同轉速條件下，軸承初始氣膜間隙對氣膜溫度的影響.從圖7中可看出，初始氣膜間隙對于軸承溫度有較大影響，尤其是在高轉速情況下，隨著間隙值減小，軸承溫度有更顯著升值.因此對于高轉速工作條件的軸承，溫度控制與裝配間隙的選取應該得到足夠重視.

圖6 軸承峰值溫度隨外部冷卻流量的變化趨勢Fig.6 Bearing peak temperature changing with external cooling flux

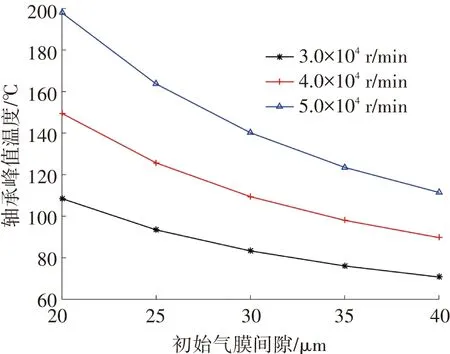
圖7 軸承峰值溫度隨初始氣膜間隙的變化趨勢

Fig.7 Bearing peak temperature changing with initial normal clearance

2.5 靜態性能分析

圖8為不同轉速條件下，分析采用等溫模型與THD模型時，波箔軸承最小氣膜厚度隨靜態載荷的變化趨勢.從圖8中可以看出，對于等溫模型或THD模型，最小氣膜厚度相同時，較高的轉速能夠獲得較大的承載能力，這是由于氣膜在高轉速時具有更強的流體動壓效應.同時，相同轉速、最小氣膜厚度條件下，THD模型預測的軸承承載力較大，這是因為非等溫條件下氣膜黏度會隨著溫度升高而增大，而且軸承結構熱膨脹會減小初始氣膜間隙，起到預緊作用，從而增大了氣膜的動壓效應.

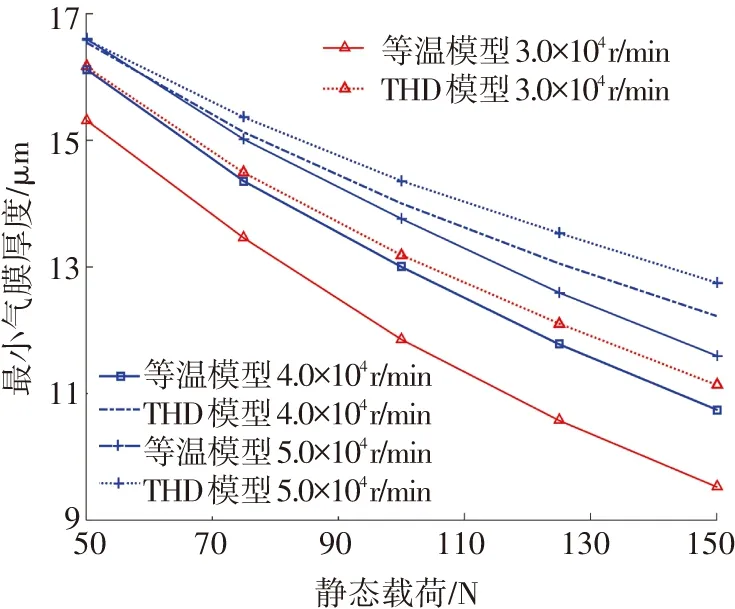
圖8 等溫模型與THD模型最小氣膜厚度隨載荷變化趨勢

Fig.8 Minimal film thickness changing with bearing load at different rotor speed

2.6 動態性能分析

圖9(a)對比分析了軸承轉速為5.0×104r/min，轉子偏心為10 μm時，等溫模型與THD模型的主動態剛度系數Kxx與Kyy隨渦動頻率比γ的變化趨勢.從該圖中可以看出，x與y方向的動態剛度系數直接項均隨γ的增大呈先減小后增大的變化趨勢，在γ為0.5附近存在最小值; 當γ>1時，剛度系數的變化趨勢變緩.理論上載荷方向y的動剛度較大，但當偏心較小，非載荷方向具有較大剛度.當γ<0.5時，THD模型的動剛度較小; 反之，THD模型計算理論值較大.

圖9(b)對比分析了相同條件下，動態阻尼系數Dxx與Dyy隨γ的變化趨勢.可以看出，x與y方向的動態阻尼系數直接項均隨γ的增大呈先增大后減小的變化趨勢，在γ為0.5附近存在最大值; 當γ>1時，阻尼系數的變化趨勢變小.載荷方向y的動阻尼較大，當γ<0.5時，THD模型的動阻尼較小; γ>0.5時，THD模型計算理論值較大.

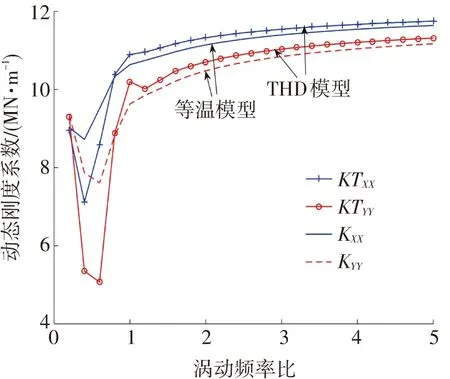
(a)動態剛度系數隨渦動比變化

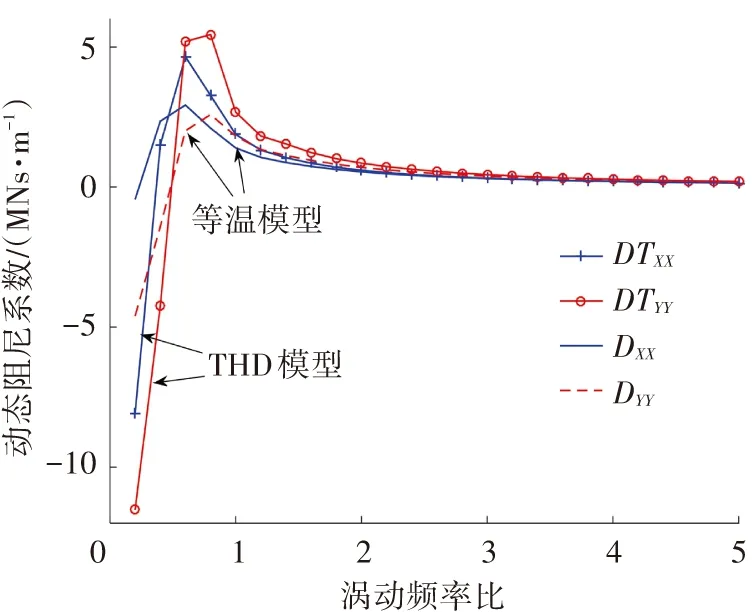
(b)動態阻尼系數隨渦動比變化

Fig.9 Dynamic stiffness and damping coefficients changing with the rotor whirl ratio

圖10 (a),(b)為給定載荷為50 N、γ為2條件下，動態剛度與阻尼系數隨轉速的變化趨勢.從圖10可看出，隨著轉速增加，動態阻尼總體上逐漸減小, 動態剛度逐漸增大.除了載荷方向的主阻尼外，當轉速較高時，THD模型計算的動態剛度與阻尼系數較大.

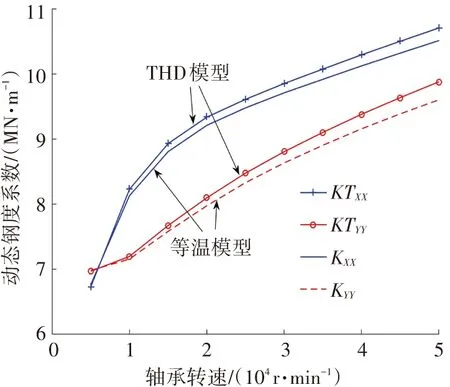
(a)動態剛度系數隨轉速變化趨勢

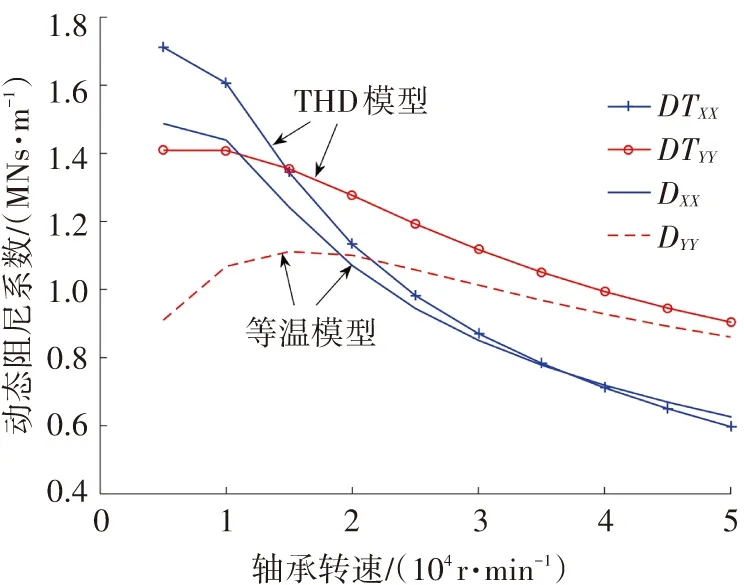
(b)動態阻尼系數隨轉速變化趨勢

Fig.10 Dynamic stiffness and damping coefficients changing with the rotor speed

3 結 論

1)建立了波箔氣體動壓軸承的能量傳遞模型，包括潤滑氣膜的三維能量傳遞模型，箔片結構的熱傳導與對流換熱模型，轉子與軸承套的徑向導熱模型.

2)推導了平箔片內表面的等效對流換熱系數，耦合求解了氣膜的能量方程、Reynolds方程、氣膜厚度方程，得到了氣膜溫度三維溫度分布，軸承結構的溫度分布.

3)通過理論計算結果與文獻中實驗數據的對比，驗證了模型與程序的準確性.

4)分析了軸承轉速、靜態載荷、外部冷卻流量、初始氣膜間隙對軸承溫度的影響.計算結果表明: 載荷對軸承溫度影響不大，轉速是影響軸承溫度的主要因素，波箔通道中通入冷卻空氣能夠有效降低軸承溫度，冷卻效率隨著冷卻流量的增大而逐漸降低，初始氣膜間隙對于軸承峰值溫度有重要影響.對比分析了等溫模型與THD模型的最小氣膜厚度隨承載力的變化趨勢，以及轉速與渦動頻率比對動態剛度、阻尼的影響.

[1] HESHMAT H.Advancements in the performance of aerodynamic foil journal bearings: high speed and load capability [J].Journal of tribology, 1994, 116(2): 287-294.DOI: 10.1115/1.2927211.

[2] AGRAWAL G L.Foil air/gas bearing technology: an overview[C]//ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition.[s.l.]: American Society of Mechanical Engineers, 1997: V001T04A006-V001T04A006.DOI: 10.1115/97-GT-347.

[3] DELLACORTE C, VALCO M J.Load capacity estimation of foil air journal bearings for oil-free turbomachinery applications [J].Tribology Transactions, 2000, 43(4): 795-801.DOI: 10.1080/10402000008982410.

[4] KIM D, KI J.Extended three-dimensional thermo-hydrodynamic model of radial foil bearing: case studies on thermal behaviors and dynamic characteristics in gas turbine simulator[J].Journal of Engineering for Gas Turbines and Power, 2012, 134(5): 052501(1-13).DOI:10.1115/1.4005215.

[5] KIM T H, LEE Y B, KIM T Y, et al.Rotordynamic performance of an oil-free turbo blower focusing on load capacity of gas foil thrust bearings[J].Journal of Engineering for Gas Turbines and Power, 2012, 134(2): 022501(1-7).DOI:10.1115/1.4004143.

[6] DYKAS B, BRUCKNER R, DELLACORTE C, et al.Design, fabrication, and performance of foil gas thrust bearings for micro turbomachinery applications [J].Journal of Engineering for Gas Turbines and Power, 2009, 131(1): 012301(1-8).DOI:10.1115/1.2966418.

[7] DYKAS B, HOWARD S A.Journal design considerations for turbomachine shafts supported on foil air bearings [J].Tribology Transactions, 2004, 47(4): 508-516.DOI: 10.1080/05698190490493391.

[8] HOWARD S, DELLACORTE C, VALCO M J, et al.Dynamic stiffness and damping characteristics of a high-temperature air foil journal bearing [J].Tribology transactions, 2001, 44(4): 657-663.DOI: 10.1080/10402000108982507.

[9] SALEHI M, SWANSON E, HESHMAT H.Thermal features of compliant foil bearings： theory and experiments [J].Journal of Tribology, 2001, 123(3): 566-571.DOI:10.1115/1.1308038.

[10]PENG Z C, KHONSARI M M.A thermohydrodynamic analysis of foil journal bearings[J].Journal of tribology, 2006, 128(3): 534-541.DOI: 10.1115/1.2197526.

[11]LEE D, KIM D.Thermohydrodynamic analyses of bump air foil bearings with detailed thermal model of foil structures and rotor[J].Journal of Tribology, 2010, 132(2): 021704(1-12).DOI:10.1115/1.4001014.

[12]FENG K, KANEKO S.A thermohydrodynamic sparse mesh model of bump-type foil bearings[J].Journal of Engineering for Gas Turbines and Power, 2013, 135(2): 022501(1-12).DOI: 10.1115/1.4007728.

[13]ANDRéS L S, KIM T H.Thermohydrodynamic analysis of bump type gas foil bearings: a model anchored totest data[J].Journal of Engineering for Gas Turbines and Power, 2010, 132(4): 042504(1-10).DOI: 10.1115/1.3159386.

[14]DELLACORTE C.A new foil air bearing test rig for use to 700 c and 70,000 rpm[J].Tribology transactions, 1998, 41(3): 335-340.DOI:10.1080/10402009808983756.

[15]RADIL K, ZESZOTEK M.An experimental investigation into the temperature profile of a compliant foil air bearing [J].Tribology transactions, 2004, 47(4): 470-479.DOI: 10.1080/05698190490501995.

[16]HOLMAN J P.Heat Transfer[M].北京：機械工業出版社，2011：191-193.DOI: 10.1016/0142-727X(82)90045-5B.

(編輯 楊 波)

Temperature calculation and static and dynamic characteristics analysis of bump foil gas bearing

LI Changlin, DU Jianjun, YAO Yingxue

(Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055， Guangdong, China)

To calculate the temperature field of bump foil gas bearing, and to analyze its thermal characteristics, considering outer cooling condition and specific foil structure, the equivalent heat convective coefficient on the inner side of top foil is derived, and the heat conductive and convective models of bearing sleeve and rotor are established respectively.Non-isothermal Reynolds equation, energy transfer equation of gas film and foil deflection equation are solved.The influences of bearing load, out cooling condition, bearing speed, etc.on bearing temperature are finally obtained, and the static and dynamic performance of the bearing is calculated.The results indicate that the bearing temperature is very sensitive to the bearing speed, and the cooling efficiency of the out cooling flow becomes weak with the increase of the cooling mass flow rate.The smaller nominal clearance plays a more important role in influencing the bearing temperature than the larger one.In addition, with the temperature effects considered, the bearing will achieve higher load capacity, larger dynamic stiffness and damping coefficients.

bump foil gas bearing; temperature field; THD model; energy transport equation; multi-field coupling

10.11918/j.issn.0367-6234.2017.01.006

2015-12-31

深圳市基礎研究(JCYJ20140417172417153); 國家自然科學基金(51675121)

李長林(1991—)，男，博士研究生； 姚英學(1962—)，男，教授，博士生導師

杜建軍， jjdu@hit.edu.cn

TH117

A

0367-6234(2017)01-0046-07