求參數范圍問題中的一類錯因分析

王會銀

（江蘇省揚州大學附屬中學）

求參數范圍問題中的一類錯因分析

王會銀

（江蘇省揚州大學附屬中學）

恒成立問題是數學中的常見問題，此類問題常與求參數范圍結合出現在高考題中，是熱點也是難點和易錯點，本文從邏輯的角度對此類問題的錯誤原因進行探析。

由導數知識可知：h（x）min=h（1）=3 ∴由①得a≤3

而φ（x）在（0，+∞）上是單調增函數且當x→+∞時，φ（x）→+∞

所以滿足條件②的a不存在.

綜合上述研究可得a的取值范圍是a≤3.

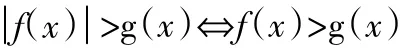
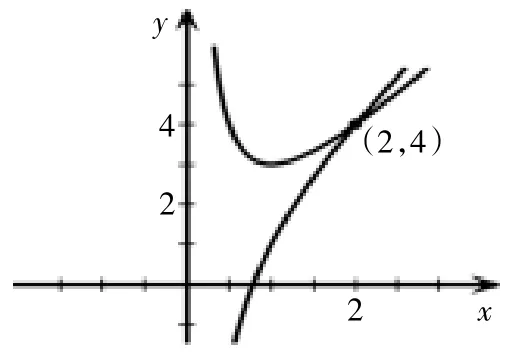
圖1

由（Ⅱ）對?x＞0成立得滿足條件的a不存在，所以a的取值范圍是a≤0

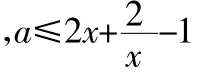
事實上，若將a換成y，我們可以從圖形的角度來分析上述解法的錯誤（線性規劃的思想）得到正確解法。

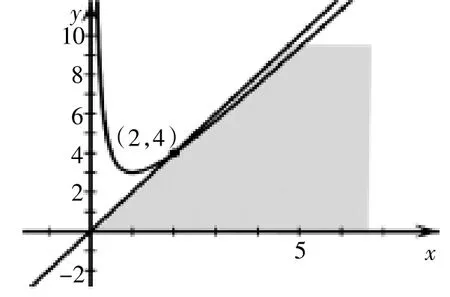
圖2

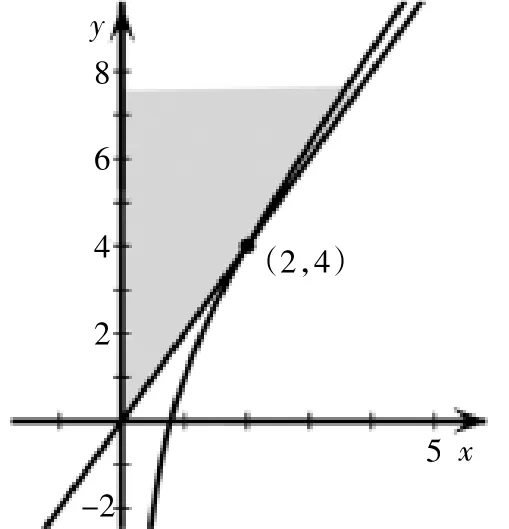
圖3

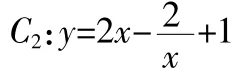
下面再給出例1的兩種正確解法。

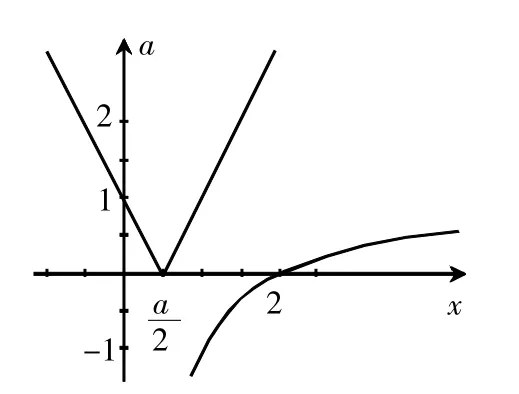
圖4

分情況討論：

所以當a≤0時f（x）≥0恒成立.

只要研究f（x）在（0，+∞）上的最小值，由導數知識可得f2（x）在（0，+∞）上是單調減函數，f1（x）在（0，1）上單調減在（1，+∞）上單調增，所以要分情況討論：

f（1x）在［，+∞）上是增函數，f（2x）在（0，］上是減函數

所以（fx）min=（f）=-1≥0 ∴a≤4又∵a≥2 ∴2≤a≤4

f（1x）在［，1］上單調減在［1，+∞）上單調增

f（2x）在（0，］上是減函數 ∴（fx）min=（f1）=3-a≥0 ∴a≤3

∴0＜a＜2時，f（x）≥0恒成立.

由上述討論可知a的取值范圍是幾種情況的并集（-∞，0］∪（0，2）∪［2，4］=（-∞，4］

總結：解法1和解法2都用到了“分離變量法”，解法4用到“研究含參函數最值法”，這兩種方法都是解決不等式恒成立問題的常用方法，前三種解法都用到“數形結合”的數學思想方法，當問題涉及的函數圖象是學生熟悉的圖像時，“數形結合”顯然是一種簡潔有效的方法。

二、形如f（a，x）g（a，x）＞0恒成立問題中的錯因分析

問題二：（浙江2012理科卷17題）設a∈R，若x＞0時均有［（a-1）x-1］（x2-ax-1）≥0，則a=___________

錯解：等價轉化為［（a-1）x-1］（x2-ax-1）≥0對?x＞0恒成立

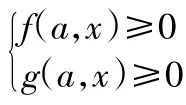
對錯解糾正可以得到下面的正確解法：

即（Ⅰ）對?x∈［2，+∞）恒成立或（Ⅱ）對?x∈（0，2］恒成立.

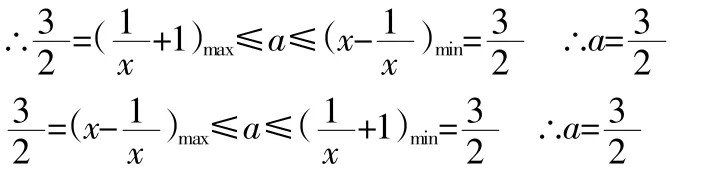
此題還有多種其他解法，下面給出其中的兩種：

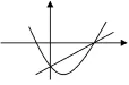
圖5

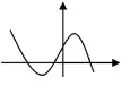
圖6

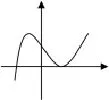
圖7

正解2：（數形結合）設y1=（a-1）x-1（x＞0），y2=x2-ax-1（x＞0）

①當a≤1時，y1＜0，y2的值在x→+∞時y2→+∞，因而不滿足y1y2≥0對?x＞0恒成立

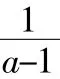
正解3：（函數與方程思想）設f（x）=［（a-1）x-1］（x2-ax-1），研究方程［（a-1）x-1］（x2-ax-1）=0（*）分情況討論：

①當a=1時，f（x）=-x2+x+1，f（2）=-1＜0，所以不符合題意

②當a＜1時，方程x2-ax-1=0有一正一負兩不等實根，方程的根（a-1）x-1=0，所以方程（*）有一正兩負的實根，由三次函數圖像（圖6）知f（x）≥0不恒成立

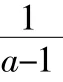
總結：上述兩例的邏輯錯誤實際上都是“或”惹的禍，即（Ⅰ）或（Ⅱ）對?x∈D恒成立不等價于（Ⅰ）對?x∈D恒成立或（Ⅱ）對?x∈D恒成立，對此類問題還是以數形結合或分類討論的方法處理較為穩妥。

羅增儒.一道不等式恒成立高考題的錯解分析［J］.中學數學教學參考，2013（9）.

●編輯 李博寧