求解二次函數幾何變換問題的解析

盧彩霞

（甘肅省蘭州市第八十三中學）

求解二次函數幾何變換問題的解析

盧彩霞

（甘肅省蘭州市第八十三中學）

北師大版對二次函數內容的學習是在一次函數、反比例函數基礎上進行的，對它的討論是從最簡單的二次冪函數開始的，研究它的圖象和性質，明確函數的三種表示形式，便于從不同側面對函數性質的覺察和從不同角度的整合中對二次函數形成整體性認識。縱觀近幾年中考試卷，二次函數的相關知識點經常被作為壓軸題在選擇題、填空題及解答題中頻繁出現，但學生往往容易失分，怎樣能夠有效得分，利用相關實例結合實踐操作多方面解答此題。

二次函數；幾何變換；實踐操作

以二次函數為背景的幾何圖形的變換問題是近年來全國各地數學中考的熱點題型，因此，備受命題者的青睞。這類試題常常需要用到數形結合思想、轉化思想、分類討論思想等，解決這類問題的關鍵就是要熟練應用幾何圖形的變換性質和二次函數的有關知識進行分析、探究，以達到考查學生綜合運用知識解決問題的能力。筆者從2016年蘭州市中考模擬數學試題中選取第15題，加以解析說明，以饗讀者。

A.3 B.3.5 C.4 D.4.5

分析：首先求得平移后的解析式，進而求得頂點A的坐標，通過分析找出滿足題目要求的P點及求得坐標，求得P點直線OA的距離，然后根據三角形面積公式即可求得。

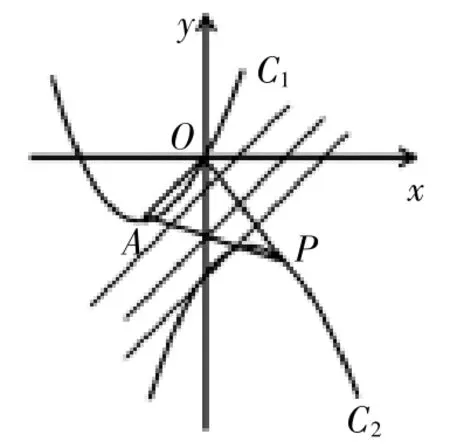
圖1

解答：方法一：

方法二：

《義務教育數學課程標準》明確指出學生學習應當是一個生動活潑的、主動的和富有個性的過程。學生應當有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程。動手實踐也是一種學習數學的重要方式之一。因此，通過實踐操作本題還有如下解法：

分析：方法一是根據平行線間垂線段最短，找到點P的位置從而滿足△POA的面積最小。現在如果換個思路，如果能在拋物線C2上找到一點到線段OA的距離最短，那么問題就迎刃而解了。

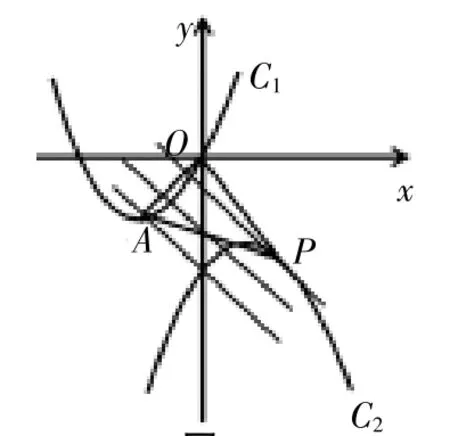
圖2

●編輯 溫雪蓮