教學案例在教學反思中的應用

摘 要課堂教學從“灌輸式”到“引導發現式”的轉變，以教師提出問題、學生探討解決問題為途徑，以相互補充展開教學，筆者從數學教學的教學案例反思中尋找出有利于教學的一種方法，旨在更好地改進教學。

【關鍵詞】教學案例；教學反思；應用

教師的反思案例是教師在對有代表性事件進行詳盡描述的基礎上，進而概括出具有一般性結論的研究方法，通過研究課堂教學中成功或失敗的課例，對成功案例要找到教育理論支撐點，并將其運用到新的課例中去；對失敗的案例找到之所以失敗的原因，避免重蹈覆轍.案例反思是教師運用教育理論，思考自己遇到過的教育事件，它需要教師有很深的理論功底和較強的思維能力.以下是我寫的一則數學教學案例反思——函數的奇偶性.

教學預案稿：學生觀察比較（1）y=2x（2）y=|x|與

（3）（4）y=x的圖象，哪兩個關于y軸對稱？哪兩個關于坐標原點對稱？（事先給出圖象）并歸納出它們之間的數量關系。

教學預案修正稿：同學們，我們生活在一個美麗的世界，大自然中的很多事物都能給我們一種美的享受，看多媒體一組圖片，請你按照一定的標準將它們進行分類。

（學生觀察、思考后，給出的分類情況多種多樣）

師：下面我們首先從軸對稱圖形開始研究。

問題：請同學們作出下列函數的圖象。

（1）y=2x； （2）y=|x| .

（巡視并選取學生畫的圖象，用實物投影進行展示）

師：觀察這兩個函數的圖象，你有何發現？

（生：關于y軸對稱）

師：你能給出驗證嗎？

（提示學生回憶在初中如何判斷一個圖形是軸對稱圖形，學生給出對折方案后，讓學生動手操作確認）

師：好！有沒有其他辦法？

（給出思考： M（x0，y0）是y=x2的圖象上的任意一點，它關于y軸的對稱點M'的坐標是什么？點M'在y=x2的圖象上嗎？學生合作探究后，請學生作簡要的證明）

下面是我和學生一起討論、共同探討研究函數的奇偶性

我們再通過“幾何畫板”展示一下，請看動畫。

（在屏幕上用“幾何畫板”作出函數y=x2圖象（點M與M'關于y軸對稱），度量點M與M'的坐標，選中度量的結果，利用圖表菜單制成表格，并添加10條表中記錄，拖動點M，得到如下數據）

M（2.04，4.14），M'（-2.04，4.14）；M（1.35，1.82），M'（-1.35，1.82）；

M（0.81，0.66），M'（-0.81，0.66）；M（-1.05，1.10），M'（1.05，1.10）；

M（-1.91，3.66），M'（1.91，3.66）；M（-1.78，3.16），M'（1.78，3.16）

M（-0.36，0.13），M'（0.36，0.13）；M（1.39，1.94），M'（-1.39，1.94）

師：觀察上表，點M與M'的坐標之間有何關系？

（學生觀察思考后，請學生予以表述，教師略作補充后得：當自變量x取一對相反數時，相應的函數值相同）

師：請大家對y=|x|進行檢驗，看是否有類似結論？

（學生動手操作并確認）

師：對于一般函數y=f（x），如果它的的圖象關于y軸對稱，那么會有什么樣的結論？

（學生分組探究，陳述各自的想法，教師分析評價，完善后給出偶函數的定義）

板書：

課題：函數的奇偶性

1.偶函數的定義：如果對于函數f（x）的定義域內的任意一個x，都有f（-x）=f（x），那么稱函數y=f（x）是偶函數.

練習1.對于定義在R上的函數f（x），下列判斷是否正確？

（1）若f（-2）=f（2），則函數f（x）是偶函數；

（2）若f（-2）≠f（2），則函數f（x）不是偶函數。

練習2.函數f（x）=x2，x∈（-1，1）是否為偶函數？

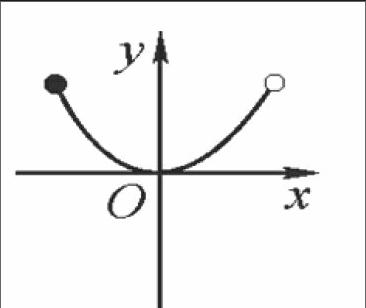
練習3.函數f（x）的圖象如圖所示，f（x）是否為偶函數？

（學生合作探究，互動完成，對偶函數概念中的關鍵之處有了統一認識）

師：我們通過對軸對稱圖形的研究得到了偶函數的定義，你能否舉些圖象關于原點對稱的函數呢？如果能，請你用類比的方法加以研究！

（學生列舉的函數有，y=x等，然后組織學生進行合作探究，通過類比的辦法，歸納出奇函數的定義以及定義中需要注意的關鍵之處）

板書：

2.奇函數的定義：如果對于函數f（x）的定義域內的任意一個x，都有f（-x）=-f（x），那么稱函數y=f（x）是奇函數。

師：圖象關于y軸（原點）對稱的函數是偶（奇）函數，是否存在圖象既關于y軸又關于原點對稱或者既不關于y軸也不關于原點對稱的函數呢？若存在，請舉例說明。

（教師引導，學生分小組討論，合作探究完成，函數按奇偶性可以分為四類：奇函數、偶函數、既奇且偶函數、非奇非偶函數）

反思：教學預案稿有“牽著學生鼻子走”的感覺，學生學習數學是被動的，沒有自己主動建構知識的機會.教學預案修正稿則在實際生活中提煉出對稱性，近而讓學生自己作出熟悉的函數圖象，進一步思考，形成結論，這種從整體到局部的認識過程，符合學生的心理認知規律。

本設計從生活中的數列模型，如建筑實物、雪花、太極圖、蝴蝶等實物引入，進而提出有待探索的問題，這有助于發揮學生學習的主動性.在探索的過程中，通過設置“問題串”，激發學生的思考欲.教師以平等的身份巡回各組中間，與學生一起學習、討論、探究.引導學生發現規律，這樣易于學生理解奇偶性的概念.本課各環節的設計環環相扣、簡潔明了、重點突出，引導分析細致、到位、適度.如：通過對題目的判斷，促進了對概念理解，同時通過類比的數學思想讓學生自己探究出奇函數的定義；還有讓學生動手畫函數圖象，從“形”的角度，感受函數的奇偶性；學生在經歷過程中，加深了對概念的理解和鞏固。

本節課教學體現了課堂教學從“灌輸式”到“引導發現式”的轉變，以教師提出問題、學生探討解決問題為途徑，以相互補充展開教學，總結科學合理的知識體系，形成師生之間的良性互動，提高課堂教學效率.教學手段和教學方法的選擇合理有效，體現了新課程所倡導的“培養學生積極主動，勇于探索的學習方式”。

參考文獻

[1]蘇霍姆林斯基.給老師的一百條建議[M].上海：華東師范大學出版社，2010：163.

[2]周龍影.教師的自我教育與反思[J].河北師范大學學報（教育科學版），2012（01）.

作者簡介

張文（1968-），女，江蘇省徐州市人。現為江蘇省徐州技師學院副教授。研究方向為數學教育。

作者單位

江蘇省徐州技師學院 江蘇省徐州市 221151