最優化方法實踐課程教學的一個案例

陳照輝，唐利明，任澤民

(1.重慶科技學院 數理學院，重慶 401331；2.湖北民族學院 理學院，湖北 恩施 445000)

?

最優化方法實踐課程教學的一個案例

陳照輝1，唐利明2，任澤民1

(1.重慶科技學院 數理學院，重慶 401331；2.湖北民族學院 理學院，湖北 恩施 445000)

最優化方法課程具有較強的實用性，對該課程實踐教學現狀進行了分析，闡述了實踐教學的必要性，提出案例教學的重要性和可行性。通過一個實踐教學實例分析案例教學，說明獨立設置上機實驗，通過老師指導，以學生為主體的案例教學，能有效發揮學生學習的主觀能動性。

最優化方法，案例教學，實踐課程，應用型

最優化方法作為應用數學專業一門核心專業課程，具有較強的理論性和實用性。該課程的實踐教學環節對培養大學生運用數學知識解決實際問題的能力起著十分重要的作用。為全面提高應用型、創新性人才培養質量，本文對最優化方法實踐教學現狀進行分析，闡述實踐教學的重要性和案例教學的可行性，通過一個教學案例的實施過程探索改革實踐教學內容和教學方法。

1 最優化方法實踐課程教學的重要性

最優化方法是一門理論性和實用性很強的專業課程，它研究如何在所有可行方案中搜索出最優方案[1,2]。該課程中所涉及到的優化方法在諸多領域中得到了廣泛的應用[3]。所以，不僅限于數學專業，其它以培養應用型人才為目標的工程技術和管理專業開設該課程，使學生掌握優化思想和對實際工程問題進行優化處理的能力，也是其需要具備的基本素質。

目前國內在最優化方法教學中，較注重一些經典的優化算法學習，在實踐教學中也是算法驗證性實驗。但是，近些年隨著科技的進步，實際工程中遇到的優化問題也越來越復雜，隨之最優化方法也得到了迅速的發展，應用也越發靈活，課本中所列的經典優化方法已不能滿足工程需要。現代優化算法如遺傳算法、模擬退火法、粒子群算法、蟻群算法等發展已較為成熟，也在很多工程領域中得到了廣泛的應用[4]。 但是，大多最優化方法教材并未列寫這些相關內容，在實際教學中也很少涉及，一般在研究生課程中才會有所體現。為了順應應用型人才培養目標，作者認為應在教學過程中適當補充一些現代優化方法的學習，側重在實踐教學中使學生掌握算法的應用方法和軟件的使用。

實踐教學是能夠讓學生從工程的角度理解優化思想的重要環節。實踐教學不但能加深對所學理論知識的理解，而且能提高理論聯系實際，解決工程問題的能力。另外，通過實踐教學，用現代化技術手段將優化理論和問題解決一同展示，對提高學生學習興趣和積極性無疑是有幫助的。實踐教學要求學生熟練掌握一門高級語言，然而，語言是其面臨的一大難題，這也正說明了實踐課程教學的重要性。

面對解決工程中的優化問題，需要首先將現實問題模型化，這一點能夠培養學生自主分析問題和將優化問題轉化為數學模型的能力。所以，篩選合適的案例是實踐教學的首要任務。為了讓實踐教學發揮出更好的效果，案例要突出較強的實戰性，同時，要緊密結合所學優化方法。另外，案例要兼顧難易度適中，并具有挑戰性，還要具有互動性，這樣才能激發學生學習探索的積極性。

2 一個實踐教學案例

車輛路徑問題(Vehicle Routing Problem，VRP)是由Dantzig和 Ramser于1959年首次提出的，屬于完全NP問題，該問題在最優化、物流管理、計算機等領域中得到了廣泛的關注和研究[5]。該問題背景清晰、易懂且具有針對性和實戰性，所以，在最優化方法實踐教學過程中選擇該問題作為一個案例。

2.1 車輛路徑問題描述與模型

一般地，車輛路徑問題可描述為：對一系列發貨點或收貨點，組織適當的行車路線，使車輛有序地通過它們，在滿足一定的約束條件下，達到一定的目標。例如，有一個中心倉庫，擁有K輛車，第k輛車的最大載重量或容量記為qk(k=1,2,…,K)，負責向L個需求點配送貨物，第i個需求點的貨物需求量為gi(i=1,2,…,L)，且maxgi≤maxqk；cij表示車輛從需求點i到需求點j的配送成本(距離、費用或時間)。求滿足需求的成本最小的車輛行駛路徑。

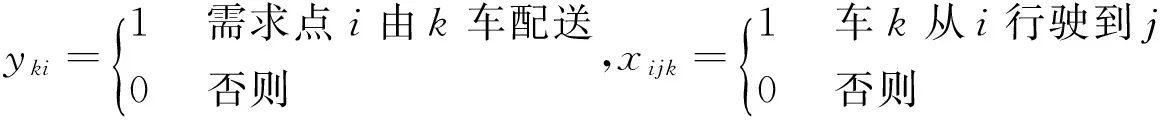
(1)

2.2 有時間窗的車輛路徑問題描述與模型

如果在上述車輛路徑問題中，增加一種約束，即完成需求點i的貨物配送必須在時間窗口[ETi,LTi]需完成，且需要的時間為Ti，其中ETi表示為需求點i配送的最早開始時間，LTi表示為需求點i配送的最遲開始時間。如果車輛到達需求點i的時間早于ETi，則車輛需要等待，增加了時間成本；如果晚于LTi到達，則需支付一定的罰金，增加了配送成本。那么，這種考慮了配送時間約束的車輛路徑問題為具有時間窗的車輛路徑問題(Vehicle Routing Problem with Time Windows，VRPTW)。

以ti表示車輛到達第i個需求點的時間，pE表示提前到達的單位時間等待成本，pL表示延遲到達的單位時間懲罰成本，則具有時間窗約束的車輛路徑問題模型中目標函數為

(2)

約束條件與(1)相同。從模型(1)(2)易知，當ETi=0，LTi→∞時，(2)等價于(1)。

3 教學分析

在最優化方法理論教學內容中，我們補充學習了現代優化算法(粒子群算法，遺傳算法)，并且熟悉了這兩種算法的用于求解無約束優化問題的軟件操作和編程實現。然后，提出車輛路徑問題，作為單獨的上機實驗環節要求用粒子群算法進行解決。具體操作如下：

a. 編碼

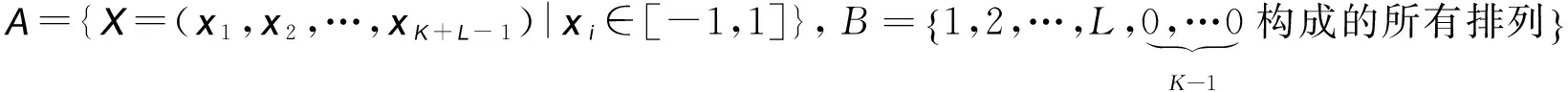
b. 構造適應值函數

(3)

其中M是充分大的數。顯然，(3)中令pE=0,pL=0便是VRP的適應值函數，其完全可用Lingo解決。

c. 算法步驟

第1步：初始化參數K,L,N,w,c1,c2,M，最大迭代次數Nmax，粒子群Xi=(xi1,xi2,…,xi,K+L-1)和初始速度Vi=(vi1,vi2,…,vi,K+L-1)，i=1, 2, …,N，其中-1≤xij≤1；

第2步：按照a中的編碼方法將Xi映射到Yi∈B,i=1, 2, … ,N；

第3步：根據(3)計算Yi點的適應值；

第4步：根據Yi的適應值，修改個體最優Pi和全局最優Pg；

第5步： 根據粒子群算法迭代式更新粒子的位置；

第6步：判斷終止條件是否滿足，是，停止迭代并輸出Pg；否，返回到第2步。

解決該問題具有挑戰性，首先需要編碼，這一步能加深學生了解相應算法；然后需要構造適應值函數，這一步能促使學生深入了解罰函數法處理約束條件；最后需要按照算法的步驟構建解決VRPTW的算法，這一步驟能夠使得學生進一步深入熟悉算法的結構和在組合優化問題中的使用方法。

在教學過程中，有的學生利用Lingo 軟件解決了VRP，在解決VRPTW中遇到了困難。大多數同學能夠在實驗中通過團隊協作，完成基本粒子群算法程序的修改，從而成功解決該問題。

4 結語

最優化方法課程中應用案例進行教學，取得非常好的效果。以學生為主體，通過對問題分析、建模、解決實現的過程，進行了師生間的互動。在老師的引導下，使得學生充分發揮其主觀能動性，不但能提高分析問題，建立模型，解決問題和編程的能力，而且能夠充分發掘學生的創新潛能。本文首先分析最優化方法實踐課程教學現狀，說明實踐教學在提高學生分析問題和解決問題能力中扮演重要角色，列舉一個案例旨在闡述最優化方法實踐課程教學的一個可操作方法。

[1] 袁亞湘，孫文瑜.最優化理論與方法[M].北京：科學出版社，1997.

[2] 郭科，陳聆，魏友華.最優化方法及其應用[M].北京：高等教育出版社，2007.

[3] 何堅勇.最優化方法[M].清華大學出版社，2007.

[4] 張火明，陸萍藍，王強.“講座式”教學方法在最優化方法課程教學中的實踐與效果分析[J].技術監督教育學刊，2009(2):6-9.

[5] 李寧，鄒彤，孫德寶.帶時間窗車輛路徑問題的粒子群算法[J].系統工程理論與實踐，2004(4):130-135.

(責任校對 謝宜辰)

10.13582/j.cnki.1674-5884.2016.11.011

20160628

重慶科技學院教改項目(201245)；湖北民族學院教學研究項目(2015JY008)

陳照輝(1980- )，男，河南周口人，副教授，博士，主要從事智能優化、系統穩定控制研究。

G642.0

A

1674-5884(2016)11-0034-03