可拉伸梁方程一致緊吸引子的存在性
王素萍,邵旭馗
(隴東學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)院,甘肅慶陽745000)
可拉伸梁方程一致緊吸引子的存在性
王素萍,邵旭馗
(隴東學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)院,甘肅慶陽745000)
考慮了當(dāng)外力項h滿足條件C*(而非平移緊時),利用一致條件(C)證明了非自治可拉伸梁方程在強(qiáng)拓?fù)淇臻gD(A)×V中一致緊吸引子的存在性.
可拉伸梁方程;一致條件(C);條件C*;一致吸引子
0 引言
假設(shè)Ω?R2是具有光滑邊界?Ω的有界區(qū)域.本文將討論并詳細(xì)證明下面非自治的非線性梁方程

一致吸引子的存在性.其中α,β,γ,k均為正常數(shù),h(x,t)和g(u)是外力項.若γ=0,g(u)=0且h(x,t)≡0,方程(1)由Woinowsky-Krieger在1950年提出,u(x,t)描述了可拉伸梁的橫向偏斜.1973年,Ball[1]在文中討論了這類問題解的存在性,唯一性,正則性及古典解的存在性,隨后作者在文獻(xiàn)[2]中利用拓?fù)浞椒鞍肴旱娜踹B續(xù)性又獲得了這類方程解的存在性及漸進(jìn)性.而文獻(xiàn)[3]給出了梁方程指數(shù)吸引子的存在性,文獻(xiàn)[4-5]獲得了梁方程在強(qiáng)拓?fù)淇臻g中全局吸引子的存在性,文獻(xiàn)[6]證明了可拉伸梁方程在弱拓?fù)淇臻gE0=V×H中的一致吸引子的存在性.類似問題的研究可參考文獻(xiàn)[7-13].本文利用一致條件(C)證明方程(1)在強(qiáng)拓?fù)淇臻gE1=D(A)×V中一致緊吸引子的存在性.
1 預(yù)備知識
假設(shè)非線性函數(shù)g滿足下面條件:存在常數(shù)C1>0,使得

令H=L2(Ω),,H和V的內(nèi)積和范數(shù)分別用(·,·),,它們的內(nèi)積被分別定義為


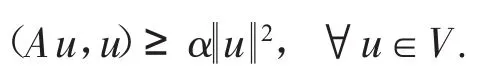
根據(jù)Poincare不等式,我們有

定義1[7]若∑是一參數(shù)集,,σ∈∑稱作Banach空間E上的過程族,如果是一個過程,即就是雙參數(shù)的映射族從E到 E滿足
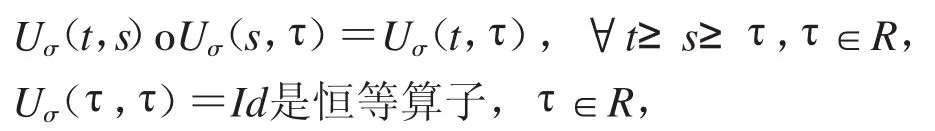
定義2[8]過程族滿足一致(關(guān)于σ∈∑)條件(C),如果對任意固定和ε>0,存在和E的有限維子空間Em,使得

其中dimEm=m和Pm∶E→Em是一有界投影,記B(E)是E的所有有界子集的集合.
i)T(r)∑=∑,?r∈R;
定理1[8]在假設(shè)I下,過程族,σ∈∑有緊一致(關(guān)于σ∈∑)吸引子,它滿足,如果它有
i)一致有界吸收集B0;
ii)滿足一致條件(C).而且,如果E是一致凸的Banach空間,則逆也成立.
引理1[9]如果,則對,則下面的結(jié)論成立
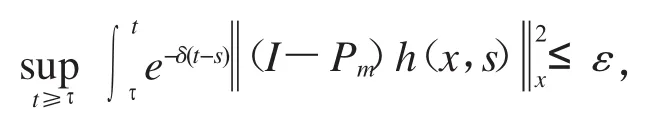
定理2[6](E0中有界一致吸收集的存在性)假設(shè)(F1)—(F3)成立,如果,則(1)式在E0中有一致吸收集.即就是,存在μ0>0,對任何有界集B?E0,存在,使得

為方便起見,我們引進(jìn)符號E0=V×H,E1=D(A)×V.
2 E1中的一致吸引子
2.1 E1中的一致有界吸收集
定理3假設(shè)(F1)—(F3)成立,如果,則(1)式在E1中有一致吸收集.即就是,存在μ2>0,對任何有界集B?E1,存在,使得

用Av=Aut+εAu乘以(1)式在H中作內(nèi)積

由(4)式,定理2,H?lder不等式及Young不等式,得
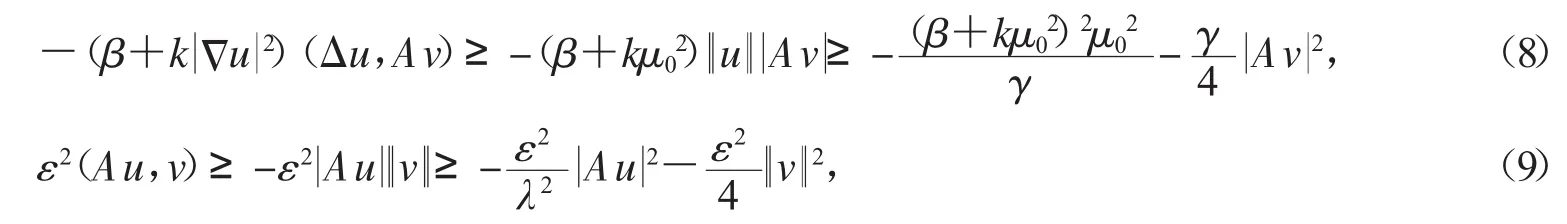
根據(jù)(F2),定理2和Sobolev嵌入定理,有g(shù)(u),g′(u)在L∞上一致有界的,即就是,存在常數(shù)K3>0,使得


結(jié)合(8)-(12),由(7)式得
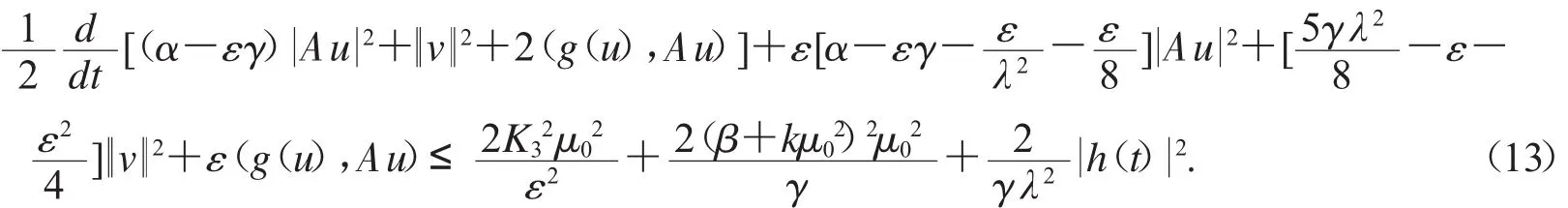
由ε的任意小,取ε>0足夠小,使得
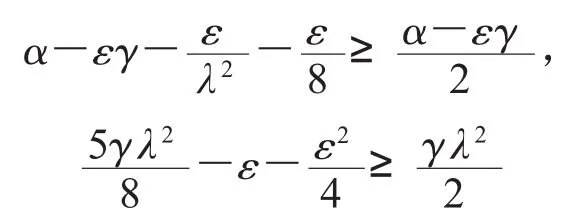
并令α-εγ=δ,則由(13)式可得

根據(jù)(9)可得

即有


因此我們得到E1中的一致吸收集B1.證畢.
2.2 E1中的一致吸引子
引理2[10]設(shè)g∈C2(R,R)且滿足(F2),則g∶D(A)→V是緊連續(xù)的.

其中B1是E1中的一致(關(guān)于h∈H(h0))吸收集.

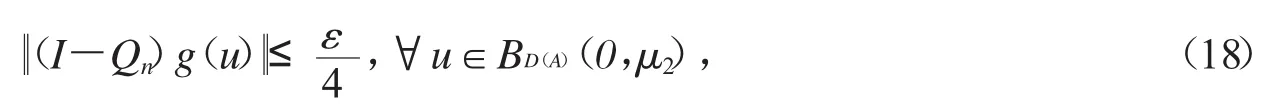
其中Qn∶D(A)→Gn都是正交投影,對任意的(u,ut)∈E1,作如下分解

取0<σ0<1,用Av2=Au2t+σAu2與方程(1)相乘,并在H中作內(nèi)積可得
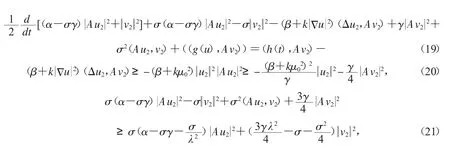

[1]BALL J M.Initial-boundary value problems for an extensible beam[J].J Math Appl,1973,42(1):61-90.
[2]BALL J M.Stability theory for an extensible beam[J].J Differential Equations,1973,14(3):339-418.
[3]王素萍,馬巧珍,邵旭馗.梁方程的指數(shù)吸引子[J].西南大學(xué)學(xué)報(自然科學(xué)版),2011,33(9):29-35.
[4]馬巧珍,孫春友,鐘承奎.非線性梁方程強(qiáng)全局吸引子的存在性[J].數(shù)學(xué)物理學(xué)報(A輯),2007,27(5):941-948.
[5]陳小豹,馬巧珍.非線性可拉伸梁方程強(qiáng)全局吸引子的存在性[J].西北師范大學(xué)學(xué)報(自然科學(xué)學(xué)報),2008,44(6):1-6.
[6]李志宇,馬巧珍.非線性可拉伸梁方程的一致吸引子[J].西南師范大學(xué)學(xué)報(自然科學(xué)版),2012,37(4):34-38.
[7]CHEPYZHOV V V,VISHIK M I.Attractors for equations of mathematical physics[M].Providence RI:Colloquium Publications American Mathematical Society,2002.
[8]ZHONG C,WU H,LU S,et al.Atrractors for non-autonomous 2d navier-stokes equations with normal external forces[J].Discrete Contin Dyn Syst,2005,13(3):701-709.
[9]MAS,ZHONGCK.The attractors for weaklydamped non-autonomous hyperbolic equations with a newclass of external forces[J].Discrete Contin Dyn Syst,2007,18(1):53-70.
[10]MAQZ,ZHONGCK.Existence ofstrongsolutions and global attractors for the suspension bridge equations [J].Nonlinear Anal,2007,67(2):442-454.
[11]MAQZ,WANGSP,CHENXB.Uniformcompact attractors for the coupled suspension bridge equations[J]. Appl Math Comput,2011,217(14):6604-6615.
[12]馬巧珍,鐘承奎.吊橋方程全局吸引子的存在性[J].四川大學(xué)學(xué)報(自然科學(xué)版),2006,42(2):271-276.
[13]ROBINSONJ C.Infinite-dimensional dynamical systems.An introduction todissipative parabolic PDEs and the theory of global attractors[M].Oxford:Cambridge University Press,2001.
Existence of Uniform Compact Attractors for the Tension Beam Equation
WANG Suping,SHAO Xukui
(School of Mathematical and Statistics,LongdongUniversity,Qingyang745000,Gansu,China)
When forcing term h only satisfies condition(C*),the existence of uniform compact attractors for the non-autonomous extensible beam equations is proved in a strong topology space E1=D(A)×V by using the uniform condition(C).
extensible beam equations;uniform condition(C);condition(C*);uniform attractors.
O175.15
A
1001-4217(2016)04-0057-07
2015-12-17
王素萍(1981—),女,甘肅慶陽人,副教授.研究方向:無窮維動力系統(tǒng)及偏微分方程的研究. E-mail:shwangsp@163.com
國家自然科學(xué)基金資助項目(11161402);甘肅省高等學(xué)校科研項目(2015A-147);隴東學(xué)院青年科技創(chuàng)新項目(XYZK1401).

