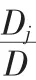啟發式教學法在線性代數教學中的應用研究
——以Cramer法則為例
楊涌 文軍 海昕
(國防科學技術大學理學院)
啟發式教學法在線性代數教學中的應用研究
——以Cramer法則為例
楊涌 文軍 海昕
(國防科學技術大學理學院)
與其他數學公共課程相比,線性代數課程具有內容抽象的突出特點。以Cramer法則教學內容為例,基于教學難點,結合教學實踐和體會,探討了啟發式教學法在線性代數教學中的應用。
線性代數;啟發式教學法;數學課程
線性代數是很多工程技術知識的基礎,因此對非數學專業而言,線性代數課程是最重要的基礎數學課程之一。線性代數課程的學時一般較少,但是概念和方法很多,并且表述抽象,這樣就使一些看似簡單的基本概念和方法對于學生而言在學習時也有難理解、難掌握的感覺,從而導致學習過程中的困惑、失落和畏難情緒。
導致這種難學難懂狀態的基本原因可以從課程的特點和學生的基礎兩個方面進行分析:線性代數課程使用的教材一般注重邏輯的嚴謹性和表述的數學化,重點突出理論知識,用純數學方法和技巧來描述普適性的規律,強調培養學生的抽象思維能力;而大一新生的數學知識與思維能力還局限于中學階段,并未完全具備嚴謹的抽象理解和推理技能。因此當課程中的知識體系與學生已學知識沒有太多聯系,并且內容高度抽象,表面上與后續專業課程結合不緊密時,就會使學生對線性代數課程的認識形成難學并且不實用的直觀印象。
從一般的認知規律而言,人們對于自然現象的分析都遵從由特殊到一般,由具體到抽象的過程。如何在線性代數課程的教學中按照認知規律,以學生為中心對教學方法進行改進和完善,培養學生的學習興趣,使線性代數的教學能夠做到易教易學是近年來線性代數教學工作者關心的重點問題之一。本文結合線性代數課程教學實踐,以Cramer法則的證明為例,探討啟發式方法在實際教學中的應用。
一、對啟發式教學法的認識
啟發式教學法源于中國古代儒家的教育思想。在現代教育中,啟發式教學被認為是一種可以有效開發學生創造性,培養學生主動思考和自主學習能力的教學模式。在具體實施中強調以學生為基本出發點,發揮好老師的主導作用,無論對學生還是老師都提出了更高的要求。
啟發式教學法的實施就是教師從學生已有知識和思維模式出發,通過創設具有啟發性的情境以及適時的思維指導,激活學生的思維,引導學生主動思考并達成教學目標。
線性代數課程旨在培養學生的抽象思維和形象思維能力以及學會把握這兩種思維之間的聯系,讓學生探索對數學問題本質的理解,提高學習的主動性和解決問題的能力。因此能否將抽象的知識理論與學生認知結構中已有的知識建立起自然而內在的聯系,直接決定了教學效果的優劣。
針對啟發式教學法和線性代數課程教學的要求,在線性代數教學中引入啟發式方法,引導學生將思維和情感融入教學過程中,從而生成積極而有效的教與學的有機過程將明顯提高學生的學習積極性,從而改善教學效果。
二、啟發式教學法在Cramer法則證明中的應用及實效分析
本節以Cramer法則的部分教學內容為例,淺談啟發式教學法在線性代數教學中的具體應用。
教學內容:Cramer法則是我校自編教材《線性代數與解析幾何》第一章第五節的內容,具體內容如下:

其中Dj是把D的第j列換成常數列所得到的行列式,

……
(唯一性的證明略)
教學難點分析:Cramer法則的結論簡潔直觀,結論的證明過程具有高度的概括性和抽象性,具有顯著的“數學之美”,但在實際教學過程中發現,對于初學線性代數的大一新生而言要較好地理解上述證明過程具有一定的難度。
學生學情分析:學生在學習該內容之前已經在第一節中利用中學階段學習的線性方程組求解結果得到了關于二階行列式和三階行列式的相關結論;在之后的章節中已經學習過n階行列式的系統理論,已經具備了掌握上述證明過程的基本知識。但對于此時接觸線性代數知識體系只有兩周左右的大一新生,在抽象表述和思維能力方面還具有一定的局限性,要理解好證明過程具有一定的難度,特別是與多維坐標相聯系的求和抽象表示符號上難以很好地掌握。
教學難點破解:結合教學難點和學情分析,考慮到自然規律認知過程,在具體教學實施過程中引入了啟發式教學法,做如下設計: