質點運動的概率題

蔡 明●

浙江省諸暨市浬浦中學(311824)

質點運動的概率題

蔡 明●

浙江省諸暨市浬浦中學(311824)

在解排列組合與概率題時常可遇到質點的運動問題.由于這類問題以考查學生分析問題、解決問題的能力以及邏輯思維能力為主，相對而言基礎薄弱的學生就有一定的難度.本文借用一高考題拋磚引玉.

高考題：設坐標平面內有一個質點從原點出發，沿x軸跳動，每次向正方向或負方向跳1個單位，經過5次跳動質點落在點(3，0)(允許重復過此點)處，則質點不同的運動方法共有____種.(用數字作答)

本題考查了學生分析問題與解決問題的能力，考查計數原理，排列組合的基本意義，分類討論思想、等價轉化思想以及對背景新奇問題的理解中所表現出來的不同思維品質、思維能力.本題可用兩種方法進行求解.

方法一 (分類討論)第一次跳動落在(1,0)回頭跳有1種，第二次跳動落在(-1,0)再回頭有1種，經過(2,0)，(3,0)，(4,0)落在(3,0)有3種，計5種.

而事實上從試題評析報告來看本題的得分不是很理想.我想這也說明我們學生對此類問題還是顯得有點為難.為了能更好地讓我們掌握質點運動問題，筆者借此對此高考題作些演變，與同行一起探討.高考題只是讓我們求出滿足條件的種數，與排列組合問題進行結合，如若加以演變不但可與排列組合結合，而且也可融入概率知識.

演變一 指定向左、向右的概率

分析 求出經過5次跳動質點A落在點(3，0)(允許重復過此點)處的概率，也就是要明確左右的次數問題.根據方法二可知：向右方向跳動4次，向左方向跳動1次.

演變二 質點個數增加為2個

分析 將質點個數增加為兩個，提高了問題的分析難度.可將題目運用分步計數原理進行求解.

根據相互獨立事件同時發生的概率計算公式可得，

演變三 質點運動方向限制

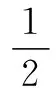
分析 將質點的運動方向加以限制，不能向上述題目一樣可用組合問題進行求解.此類還需有一定的邏輯分析能力，但可轉化為數列問題，即經n秒后質點A在x=1處的概率Pn，可由經n-1秒質點A在x=1處的概率Pn-1與不在x=1處的概率1-Pn-1來表示.

演變四 質點個數與運動方向都增加

(2)結合上圖可知至少經過2秒就可相遇，地點可在C(0,2),O(1,1),E(2,0).

從上面幾個題目的求解中可以看出對于概率類質點運動問題的求解，不但要能正確分析質點的運動過程或運動規律，而且也要能區分基本的計數原理，以及正確選用基本概率計算公式.

G632

B

1008-0333(2016)34-0022-01