ax=by=cz問題的求解

重慶市巫山中學2017級39班 易曉紅

ax=by=cz問題的求解

重慶市巫山中學2017級39班 易曉紅

對數是同學們進入高中數學學習后接觸的一類新的代數運算，就因為其運算符號的特殊性及相關字母的限制條件，使得很多同學總是望而生畏。要將對數運算作為工具運用于解題過程中，還得先了解其運算的優越性。

由于對數的運算性質知，對數運算可將積、商、乘方的運算轉化為和、差、等運算，因此對數運算可以起到降次及降低運算級別的作用，由此聯想到指數間的運算可由對數運算進行轉化。

下面就指數式中的一類題型加以探討：

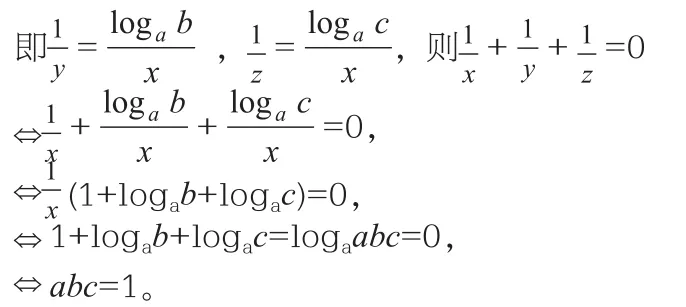
下面來看定理的應用：例1 已知：2x=3y=12z，求x、y、z滿足的一個關系式。

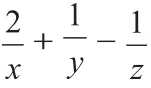
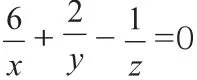
例3 已知，a、b、c為不等于1的正實數，x、y、z為非零實數，ax=by=cz，且xy+2yz-3xz=0，求證2lga-3lgb+lgc=0。

解：∵x、y、z為非零實數，且xy+2yz-3xz=0，

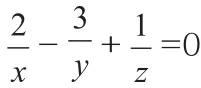
由 推 論 知：a2b-3c=1， 兩 邊 同 取 常 用 對 數 得：2lga-3lgb+lgc=0。

小結：若a、b、c為不等于1的正實數，x、y、z為非零實數，且ax=by=cz，則mxy+nyz+sxz=0的充要條件為nlga+slgb+mlgc=0。