高中數學解題中變式訓練模式的應用

江西省南昌市第二中學高三（4）班 周伊宸

高中數學解題中變式訓練模式的應用

江西省南昌市第二中學高三（4）班 周伊宸

隨著課程改革的深入，高中數學課程中我們高中生的解題要求也面臨著全新的局面。我們要想能夠更好地掌握高中數學的解題技巧，提高解題能力，就需要對訓練方法進行改變和創新。變式訓練模式能夠有效減輕在學習過程中的壓力，實現提高解題效率、優化學習質量的目的。下面我對變式訓練模式在高中數學解題中的應用進行討論。

一、改變條件特殊化

在高中數學解題的學習過程中，對于題目給出的條件往往是我們解題的關鍵。因此我們需要將題目中的條件進行特殊化的改變，使得變式訓練具有特殊性，對幫助我們解決數學問題提供更大的幫助。老師可以幫助我們將課本上的數學習題進行特殊化處理，使得它們更符合我們的學習特點，這樣能夠幫助我們更好地掌握數學知識的運用。例如，原題：根據函數f（x）=5x2+7x+12畫出圖像，并對其單調性進行分析。我們可以將題目進行變式，改為：畫出函數f（x）=5x2+7x+12的圖像，并分析函數的主要單調區間，并說明在各個單調區間上函數的變化性質。這樣雖然只是很小的變動，但是對于激發高中生認真觀察的能力，進行深入思考具有重要的作用。另外，對題目條件的變式還可以通過改變題目的背景將題目進行變式，深化題目的問題，使其具有更好的訓練效果。高中學生在解答數學題目的時候，要爭取每做一道題都有收獲，這樣才可以讓他們在學習數學的過程中越來越順利，同時，變式訓練能夠有效激發學生的發散思維。為了更好地提高應用數學知識解決實際問題的能力，我們一定要靈活掌握變式訓練的技巧。例如，還是分析函數f（x）=5x2+7x+12，如果將函數變為f（x）=ax2+bx+c，那么我們要對其單調性進行分析又該怎么做？這樣能夠訓練學生綜合考慮問題條件的能力，學生通過這樣的變式訓練，能夠有效提高我們在實際解題過程中的應變能力，減小失誤。對于提升高中數學解題質量，提高解決數學問題的能力具有重要的作用。因此，改變特殊化題目的條件在變式訓練模式中是一種有效的方法。

二、訓練思維發散性

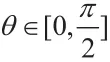
三、問題表達巧處理

在高中數學解題的訓練過程中，除了需要處理題目中各種條件的聯系，還可以通過對題目的表達進行變式，讓變式訓練的形式更豐富，增加我們解題過程中的樂趣，也就是同一道題目我們可以在不同的場景，用不同的方式提出來，從而考查我們的應變能力和適應能力。一般是變化敘述題目的方法，例如，原題：已知存在兩點M（-5，1）和N（3，1），如果還存在一點O（x，y），M，N，O三個點始終能夠形成一個直角MON，求點O的變化路徑。通過觀察題目，我們發現這是一個求動點運動軌跡的題，但是有時候這樣的敘述方式不夠直觀，因此我們可以變換一種敘述方式為：已知定點M（-5，1）和N（3，1），現在有一動點O（x，y），連接OM，ON，則始終有OM⊥ON，求O點運動的軌跡。這樣看來，我們就比較容易一眼看出題目是要求什么了，并且根據條件我們能夠形成更直觀的理解，然后在坐標系中通過畫圖幫助我們解題。這種以原題為基礎的變式訓練是比較基礎的，但是為了更好地利用變式訓練，我們還可以在不同的情景中進行應用。我們的解題思維就是需要我們在面對不同的問題時能夠快速地調整解題思路，然后集中所有可以利用的知識和條件進行解題。因此我們在不同的學習階段都需要對變式訓練的應用進行重視，爭取做到看到一個題目就能夠馬上聯想到在什么時候什么地方做過類似的題，雖然形式不一樣，但是應用的數學知識和解題方法是一樣的。這樣，對于我們的解題能力將會是一個巨大的提升。

總之，高中數學解題的變式訓練模式是一個需要長期堅持的過程。作為高中生，在學習的過程中一定要進行足夠的訓練，熟練掌握變式的應用技巧，這樣才可以在解決數學問題的時候做到從容不迫，切實有效地提高我們的解題能力。