《通過計算探索規律》教學設計

江蘇省淮安外國語學校 管金紅

《通過計算探索規律》教學設計

江蘇省淮安外國語學校 管金紅

【教學目標】

1.知識技能：運用計算器探索、發現一些數字運算結果的規律，感悟數學發現的某些方法。

2.數學思考：培養學生觀察、歸納、概括、推理的數學能力，培養學生學習數學的興趣和探索意識。

3.情感態度：讓學生感受到信息化時代，計算器（或計算機）是探索數學知識的有力工具。

【教學重點】運用規律進行計算。

【教學難點】發現規律。

【教學方法】引導發現法、談話討論法、講練結合法。

【學習方法】自主探索、動手實踐、合作交流、展示辯論。

一、提前完成導學案，視頻助學。

二、借助導學案，引導學生展示預習成果，解決問題，提出質疑。

活動1 ：計算――感悟

1.（1）觀察下列各式：

3×5= 33×35= 333×335= 3333×3335=

（2）計算并寫出（1）中各式的結果。

（3）你能發現（1）中各式的結果有什么規律嗎？

（4）根據你發現的規律嘗試填寫下列空格：

3333333×3333335=____________；

______×_____________ =1111111155555555。

（5）請你驗算（4）中的式子是否正確。

2.（1）下列各式是個位數字為5的整數的平方運算，各等式右邊數的末兩位數字有什么特點？觀察各式中其余數位上的數字，你有什么發現？

（2）根據你發現的規律，寫出下列各式的結果：

752=______，952=______，1152=______，1952=______。

（3）驗算（2）中各式的結果是否正確。

3.（1）計算：利用計算器計算，并將計算結果直接填寫在橫線上：

31=______，32=______，33=______，

34=______，35=______，36=______，

37=______，38=______。

她總是彬彬有禮，說話輕聲細語，我卻是個大老粗；她總是氣質優雅，而我剛從武行變成明星，終于可以享受大把花錢的奢侈生活，恨不得買一堆金鏈子掛在身上；她喜歡一個人出門，享受私人空間，但我總是愛熱鬧，喜歡那種有一群人跟隨的感覺，覺得自己像個老大，走到哪都有人畢恭畢敬地幫我拿衣服、拉椅子。

（2）在上述計算結果中，其個位數字有什么規律？

（3）你發現的規律對于39、310、311、312、…、320都成立嗎？

（4）你能知道32015的個位數字是什么嗎？

活動2：展示――交流

1.小組內同學之間互相交流：①分別說說上述三個問題的特征以及發現的規律；②應用發現的規律解決問題，交流方法。

2.推薦小組優秀代表在全班交流：①上述三個問題的規律是什么？如何發現的？②這三個活動的規律探索有什么共同特征？你積累了什么經驗？③你還能提出什么問題？

活動3：問題解決

1.（1）計算：9×6=_____，99×96=_____，

999×996=_____，9999×9996=_____，

99999×99996=______。

（2）探討計算中的規律 。

2.先請你計算下列各式：

21×29=______，34×36=______，

42×48=______，83×87=______，

75×75=______，85×85=______。

（1）比較上述活動探究中的計算式子，你有什么新的發現？

（2）再多寫些有上述式子特征的算式，驗證你的發現。

3.3100的個位數字是幾？還有其他想法嗎？32013的個位數字呢？

活動4：問題發散

舉例說明數學或生活中，哪些問題的規律可以通過“計算、觀察、猜想”得到，與同伴交流。

活動5：問題拓展

閱讀下面的材料，并完成填空。

你能比較兩個數20132014與20142013的大小嗎？為了解決這個問題，現將問題一般化，即比較nn+1和（n+1）n的大小（n≥1，且n是整數），然后從分析n=1、2、3、4、5…這些簡單情況入手，從中發現規律，經過歸納猜想得出結論。

（1）通過計算比較下列各組兩個數的大小（在橫線上填“＞”“＜”或“=”）。

①12______21； ②23______32；

③34______43；④45______54；

⑤56______65。

（2）通過總結上述算式的規律，猜想結論：nn+1______（n+1）n

活動6 ：總結收獲

在本節課的探究過程中，你有哪些感受與收獲？回顧你的探究心路歷程，請將你的探究經驗、感悟和發現寫成數學小論文。

三、變式練習、小組展示

1.(2014揚州)設a1，a2，…，a2014是從1，0，－1這三個數中取值的一列數，若a1＋a2＋…＋a2014＝69，(a1＋1)2＋(a2＋1)2＋…＋(a2014＋1)2＝4001，則a1，a2，…，a2014中為0的個數是___。

2.觀察下列等式：

9-1=8；

16-4=12；

25-9=16；

36-16=20；

……

這些等式反映了自然數間的某種規律，設n(n≥1)表示自然數，用關于n的等式表示這個規律為 ____________________ 。

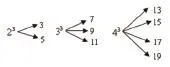
3.（2012菏澤）一個自然數的立方可以分裂成若干個連續奇數的和，例如：23，33，和43分別可以按如圖所示的方式“分裂”成2個、3個和4個連續奇數的和，即23=3+5；33=7+9+11；43=13+15+17+19；……；若63也按照此規律來進行“分裂”，則63“分裂”出的奇數中，最大的那個奇數是_____。

4.觀察下列順序排列的等式：

9×0＋1＝1；9×1＋2＝11；9×2＋3＝21；

9×3＋4＝31；9×4＋5＝41……

猜想：第21個等式應為：___。

四、學生小結

五、板書設計

六、當堂測試