產業關聯網絡演變與影響機制研究
——基于北京市12個年度投入產出表的分析

李 茂

產業關聯網絡演變與影響機制研究
——基于北京市12個年度投入產出表的分析

李 茂

產業關聯網絡的演變是產業經濟研究的前沿問題。以北京市為例，利用該市12個年度的投入產出表構造產業關聯網絡模型，展示產業關聯網絡的演變格局，進而計算和比較產業關聯網絡模型拓撲特征的變化。通過計算與比較發現：產業關聯網絡的整體布局演變呈現稀疏化特征，網絡的平均度和平均路徑長度呈現“W”形變化，聚類系數演變顯示出“M”形變化過程。進一步的機制分析發現，地區經濟總量水平和地區專業化程度負向影響網絡中節點連接強度，經濟發展方式的轉型升級對產業關聯網絡節點距離產生負向影響。地區經濟外向型水平提升使得北京產業關聯網絡中的環向連接數量降低，導致網絡連接的稀疏化問題。針對以上結論，最后給出有關產業經濟發展的政策建議。

產業關聯； 復雜網絡； 拓撲特征； 演變； 影響機制

一 引 言

產業關聯(Industrial Relations)是指經濟活動中各產業之間存在和發生的廣泛、復雜和密切的技術經濟聯系。這種聯系以產業間的投入與產出、供給與需求的數量關系為主，反映著各產業間量的關系。各個產業在中間生產過程中相互影響、相互制約，構成一個動態系統。分析這一動態系統內部的關聯狀況，有助于深入了解各產業的發展水平，為各產業發展決策提供依據。Leontief(1936)[1]提出利用投入產出法分析產業關聯，即通過編制投入產出表，建立相應的線性代數方程體系，綜合分析和確定國民經濟各產業之間錯綜復雜的聯系。此后，產業關聯一直是技術經濟領域的研究熱點(Hayter, 2015[2]; Fang, 2014[3]; Morris, 2011[4]等)。

隨著經濟發展水平提高和國民經濟部類變化，產業之間的關聯變得多樣化和復雜化，傳統的投入產出分析遇到了技術瓶頸：投入產出分析主要采用線性代數等理論，難以描述產業關聯中的整體情況，也難以表述產業關聯內部的集群關系、多元流向關系等。隨著技術經濟研究中跨學科理論的引入，學術界逐漸認識到可以利用復雜網絡理論對產業關聯進行研究，建立產業關聯網絡(Industrial Relations Network)理論。該理論對深入研究產業關聯來說有重要的理論意義與實際價值：首先，有助于詳細分析和闡釋產業關聯的內部結構、發展特征，以及一些重點關系；其次，有助于探究不同生產部類之間的聯系，揭示產業發展過程中的內在規律，并通過可視化的形式展現產業關聯網絡的總體連接情況；最后，有助于拓寬學術界對產業關聯的認識范圍，加深對不同產業生產過程中技術聯系的理解，同時為區域產業升級、產業轉移以及產業集群發展提供理論支撐。

本文借鑒已有研究成果，以北京市為例，采用歷時態的方法對產業關聯網絡進行比較分析，并對產業關聯網絡的演變影響機制進行深入探討。與已有研究成果相比，本文創新點在于：首先，改進了產業關聯網絡模型的建構方法，綜合考慮產業關聯的實際情況，以北京市這一代表性地區為例，構造出產業關聯有向有權網絡模型，同時從實際情況出發提供一個更為準確地描述產業關聯網絡連接情況的方法。其次，采用歷時態分析方法，分析產業網絡的演變情況。全面而有重點地比較12個年度的北京產業關聯網絡的總體布局和拓撲特征，有助于提高對產業關聯網絡的認識水平。再次，利用計量模型研究產業關聯網絡演變的影響機制。最后，本文的研究結論有可能為北京產業升級和京津冀產業協同發展提供決策參考依據，在一定程度上推進其他地區的產業關聯網絡研究。

本文的內容結構安排如下：第一部分是引言；第二部分是文獻綜述；第三部分主要對現有產業關聯的建模方法進行比較，重點探討有關建模方法的改進；第四部分是數據來源與處理；第五部分是模型計算結果與分析，主要是北京產業關聯網絡的總體布局展示和拓撲特征比較；第六部分分析產業關聯網絡演變的影響機制；最后一部分是結論和政策建議。

二 文獻綜述

一般意義上，復雜網絡是指由數量巨大的節點和節點之間復雜關系共同構成的網絡結構*到目前為止，學術界還很難對復雜網絡給出一個嚴格的定義，在這就不贅述不同的定義。但學術界普遍認為復雜網絡具有網絡規模龐大、連接結構復雜、時空演化過程復雜、多重復雜性融合等特征。。復雜網絡理論與數學中的圖論有著深厚聯系，它們都是利用抽象的網絡圖結構來研究復雜系統的性質。20世紀60年代之后，復雜網絡理論又引入了統計物理學、計算機、系統工程等學科的概念、范式和研究方法，逐步成為了一門以復雜系統為研究目標的交叉學科。對于復雜網絡的研究，具有里程碑意義的研究成果如下表所示。

表1 復雜網絡研究的代表性成果

隨著研究的深入，學術界開始利用復雜網絡理論來分析產業間的關聯狀況。Campbell(1972)[10]利用投入產出表構建產業圖，并依據最小分割子圖的數量分析產業集群水平。Slater(1977)[11]改進了Campbell的方法，利用1967年美國的投入產出表數據，以圖論中的流模式方法識別了產業集群。趙炳新(1996)[12]利用圖論模型研究了產業部門中的聚落群類和產業結構的演進規律。方愛麗等(2008)[13]提出了投入產出關聯網絡模型及其統計屬性研究的基本方法與思路，并從復雜網絡的視角出發建立各產業部門之間的投入產出關聯復雜網絡模型，利用國民經濟核算司發布的投入產出數據分析投入產出關聯網絡的邊權分布、強度分布和聚集系數等主要網絡屬性，進而揭示我國國民經濟系統中各產業部門之間復雜的投入產出關聯關系。劉剛和郭敏(2009)[14]在復雜網絡范式下，以部門為節點、部門之間的投入產出直接消耗系數為連接邊，建立中國宏觀經濟多部門網絡，并在此基礎上實證研究宏觀經濟多部門網絡的拓撲性質。邢李志(2012)[15]通過投入產出理論建立反映區域產業結構演化的復雜網絡模型，利用度分布、權分布和網絡路徑長度等概念對產業結構的網絡拓撲特征進行分析。侯明和王茂軍(2013)[16]利用2010年北京42個部門的投入產出數據，建立前向產業關聯模型和后向產業關聯模型，分析北京產業關聯網絡的一些特征性質。李茂(2016)[17]利用2012年北京42個部門的投入產出表，建立有向無權的產業關聯網絡模型，分析2012年北京產業關聯網絡的拓撲特征。

綜上，前人在理論與應用方面的一些創新性研究，既豐富了復雜網絡理論的內涵，也擴展了其實際應用，體現了很好的應用價值。然而，已有研究仍存在以下幾個方面的問題：第一，分析了產業關聯網絡的某些拓撲特征，說明了其所屬的復雜網絡性質，但并沒有揭示這些特征的產業經濟學涵義；第二，有些研究以直接消耗系數矩陣為模型研究基礎，但這種方法還不完善，不能反映出產業關聯的內在特征，存在許多有待改進的地方；第三，已有研究均為對靜態時點產業關聯的考察，沒有進行動態時點的分析，而通過比較不同時間點上的產業關聯網絡特點、拓撲特征與社團結構，可以挖掘產業關聯的內部聯系和動態變化。

三 建模方法與改進

(一)產業關聯網絡建模的基本方法

產業關聯網絡的建模基礎是投入產出表。投入產出表分為價值型投入產出表和實物型投入產出表兩種，價值型投入產出表以國民經濟同類產品的集合為產業進行編制，用統一的貨幣單位反映各產業之間的投入與產出關系的表格。從現有研究成果來看，產業關聯網絡建模所使用的投入產出表均為價值型投入產出表，其一般形式見表2。

表2 價值型投入產出表的一般形式

如表所示，投入產出表的左上部分(也稱為第一象限)Xij為中間產品象限(也稱為基本流量表)，它是投入產出表的基本象限，反映國民經濟各產業之間總體的經濟技術聯系。對于具體的xij，從橫行看表示的是i產品分配給j產業做生產使用的價值量，從縱列看表示的是j產業生產中消耗的i產品的價值量。處于第一象限的Xij是一個n×n的矩陣，如果將不同的產業視為節點的話，那么對Xij矩陣進行一定的處理，可以構建起反映節點間聯系的鄰接矩陣。以鄰接矩陣為基礎，經過一定的改造可建立起一個以不同產業為節點，以它們之間的經濟技術聯系為連邊的產業關聯網絡。

從上可知，產業關聯網絡的建模需要三大基礎：第一，是完成編制的價值型投入產出表，這是搭建模型的基本材料；第二，由投入產出表中的不同部門代表不同節點(Nodes)；第三，利用一定的規則對中間產品象限Xij進行改造，以構造節點之間的連邊(Edges or Arcs)。可以發現，投入產出表和投入產出表中的部門是外生的，是建模前就已經確定的，只有連邊依賴于建模中連接規則。也就是說，不同的連接規則決定不同的連接數量與類型，進而對隨后的分析和比較帶來不同的結果。

(二)已有連接規則的比較

從現有研究成果來看，節點之間連接規則主要有以下幾種方法，詳見表3：

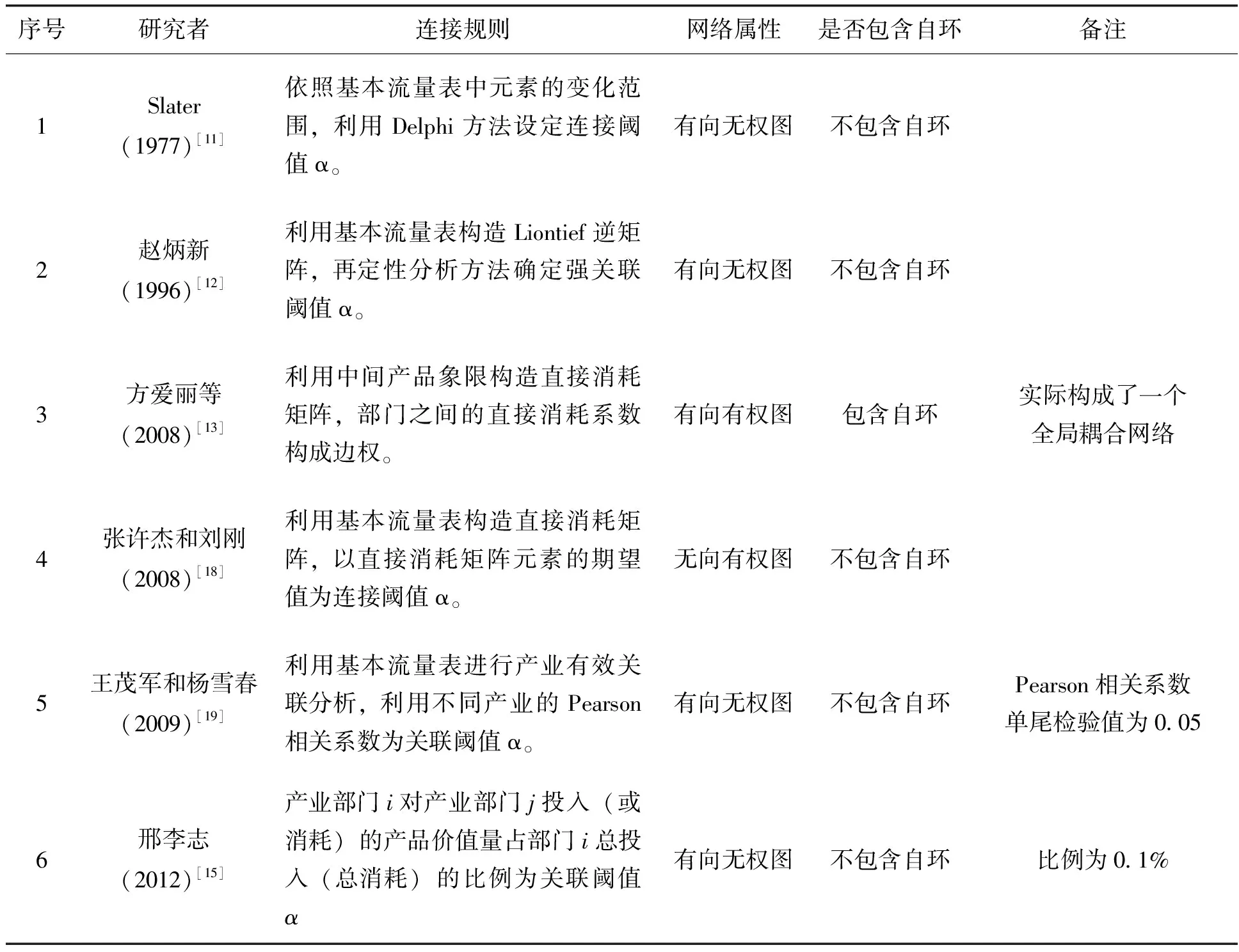
表3 有關連接規則的比較

從已有連接規則來看，可以發現以下經驗：第一，兩個部門之間的連邊需要設定合適的閾值。否則產業關聯網絡就會成為一個全局耦合網絡*全局耦合網絡的拓撲特征為常數值，不具備演化研究意義。，閾值偏小會導致連邊過于冗余，不利于分析產業關聯中的顯著關系，設定過高又會剔除部門之間的顯著聯系。第二，有向有權網絡是較好反映產業關聯中流量方向的模型。由于產業關聯中不僅存在著前向關聯、后向關聯和環向關聯，而且存在連接強度與大小的區別。因此，有向有權網絡模型是比較貼切反映實際情況的模型。第三，產業關聯網絡模型中不應包含自環。產生自環的原因就是中間消耗矩陣或者直接消耗矩陣對角線元素沒有消除。由于產業關聯網絡模型的理論前提就是節點不存在自環關系，因此部門內部的投入產出關系不在產業關聯網絡研究視閾之內。

(三)對連接規則的改進

基于已有研究成果，本研究對連接規則作以下改進：

第一，以完全消耗系數矩陣Bij作為鄰接矩陣構造的基礎。之所以選擇完全消耗系數矩陣，是因為在產業關聯網絡中各種產品在生產過程中除有直接的生產聯系外，還存在間接的聯系；各種產品間的相互消耗除了直接消耗外，還存在間接消耗。完全消耗系數則是對這種直接消耗和間接消耗的全面反映。與直接消耗系數相比，完全消耗系數揭示了部門之間的直接聯系和間接聯系，因而它能更全面、更深刻地反映出部門之間相互依存的數量關系。完全消耗系數矩陣由直接消耗系數矩陣Aij計算得出，而直接消耗系數矩陣由第一象限的Xij計算得出。

第二，剔除對角線元素設定關聯閾值。如前所述，閾值的設定不能偏小，不然會帶來連邊冗余，使得重要關系被繁蕪的聯系所“掩蓋”。一些研究不剔除不顯著的關系，完全利用直接消耗矩陣去構造鄰接矩陣，帶來了模型中節點連接的冗余問題。同樣，閾值的設定又不能偏大，否則就會剔除某些重要關系，導致連邊“失真”。在已有研究中，一些閾值的設定，考慮了中間消耗矩陣或者是直接消耗矩陣對角線元素，卻帶來設定值較高的問題。因此，關聯閾值的選取十分重要。借鑒已有研究，本文采用以下方法選取閾值：

計算得到完全消耗系數矩陣Bij后，設定兩個節點i，j之間的連接閾值Θ為完全消耗系數矩陣中剔除了對角線元素后的剩余元素的平均值①，即：

(1)

第三，為了保留產業關聯中的前向、后向與環向關聯信息，本文采用有向有權網絡模型。這樣就能使得產業關聯中的價值流向在總體布局圖中顯現出來，給研究者以直觀的印象。為了保留兩個不同節點(代表兩個不同的生產部門)的中間投入消耗關系(連邊方向)，Bij不做上三角矩陣化和對稱矩陣化處理*換言之，Bij中的元素bijj來和bji具有不同含義。前者表示，i產品分配給j產業做生產使用所消耗的完全價值量，反映了前向關聯，后者表示是j產業生產中消耗的i產品的完全價值量，反映了后向關聯。一般而言，bijj≠bji。。為了保留兩個不同節點(代表兩個不同的生產部門)之間的連接強度信息(邊權)，以上式的Θ為閾值將Bij轉化為鄰接矩陣Eij，轉化公式如下：

(2)

從式(2)可以看出，大于閾值的節點連接(部門之間的完全消耗系數)被保留下來，并作為連接的權重，小于閾值的連接信息被剔除，從而最大效果地保留了產業關聯中部門聯系的信息。

由以上討論，本文提出的模型建構規則主要有以下幾個：(1)選取投入產出表的中間消耗矩陣作為基礎材料；(2)將投入產出表中n個不同部類視為n個不同的節點；(3)利用中間消耗矩陣去計算Leontief逆矩陣，進而得到完全消耗矩陣Bij；(4)設定兩個節點i，j之間的連接閾值Θ為完全消耗系數矩陣Bij中剔除了對角線元素后的剩余元素的平均值；(5)以Θ為閾值將Bij轉化為鄰接矩陣Eij，構造出產業關聯網絡模型G(n,Eij)。

四 數據來源和模型建構

(一)數據來源

本文所用的北京市投入產出表來自“北京2012年投入產出調查網” (http://www. bjstats.gov.cn/2012trcc/)中的“歷史數據”專欄。北京市投入產出數據最新截止到2012年，該數據于2014年10月公布。采集的投入產出表數據的年份是1985年、1987年、1990年、1992年、1995年、1997年、2000年、2002年、2005年、2007年、2010年、2012年等12個年份。

由于統計口徑的變化，1985年北京投入產出表包含68個部門；1987年、1990年、1992年、1995年北京投入產出表包含33個部門；1997年和2000年北京投入產出表包含40個部門；2002年、2005年、2007年、2010年和2012年北京投入產出表包含42個部門。

(二)數據處理

利用投入產出表中的基本流量表可以計算出Leontief逆矩陣(I-Aij)-1，Leontief逆矩陣減去單位矩陣I可得到完全消耗系數矩陣Bij，計算公式如下：

Bij=(I-Aij)-1-I

(3)

(三)模型建構

按照前面改進的方法，將投入產出表中n個不同部類視為n個不同的節點。利用中間消耗矩陣去計算Leontief逆矩陣，進而得到完全消耗矩陣Bij。設定兩個節點i，j之間的連接閾值Θ為完全消耗系數矩陣Bij中剔除了對角線元素后的剩余元素的平均值。以Θ為閾值將Bij轉化為鄰接矩陣Eij，這樣可以建構12個不同年度的北京產業關聯網絡模型。為了區別，分別命名為G1985(n,Eij)、G1987(n,Eij)、……G2012(n,Eij)。

五 以北京市為例的產業關聯網絡演變

(一)整體布局演變

利用網絡分析軟件Pajek繪制出12個年度的北京產業關聯網絡整體布局情況。為了便于比較，布局方法采用學術界通用的鐮田—河合(Kawada-Kawai)方法。整體布局演變情況如下：

由圖1*由于關聯網絡圖中節點較多且較復雜，如需更清晰的圖片可與作者聯系。可見，除了節點數量有著不同之外，北京市產業關聯網絡的整體布局演變呈現出一個顯著的特征：即在具體布局上經歷了一個“密集—稀疏—密集—稀疏”的演變過程，但在總體布局上呈現出稀疏化趨勢。下面用具體的拓撲特征去表述這種演變過程。

(二)拓撲特征的演變

復雜網絡具有規模龐大、連接結構復雜、時空演化過程多樣、多重網絡復雜性融合的特點，這些特點統稱為復雜網絡的拓撲特征，學術界主要采用指標描述的方式去刻畫這些特征。參照Albert和Barabási(2002)[8]的研究，本文所要計算的拓撲特征主要有以下3類(見表4)。

②需要指出的是，節點i的度Ki定義為與節點i直接相連的邊的數目，網絡中所有節點的度的平均值稱為網絡的平均度。在模型中，每個節點的度是由Pajek 程序計算得出的。

③dij定義為連接i節點與j節點的最短路徑上的邊的數目，而i節點與j節點最短路徑指的是連接這兩個節點的邊數最少的路徑。在模型中，dij是由Pajek 程序計算得出的。

④ 在模型中，節點i 的Fi 是由Pajek 程序計算得出的。

利用復雜網絡分析軟件Pajek軟件對數據進行計算，12個年度的拓撲特征演變情況如表5及圖2、圖3、圖4所示：

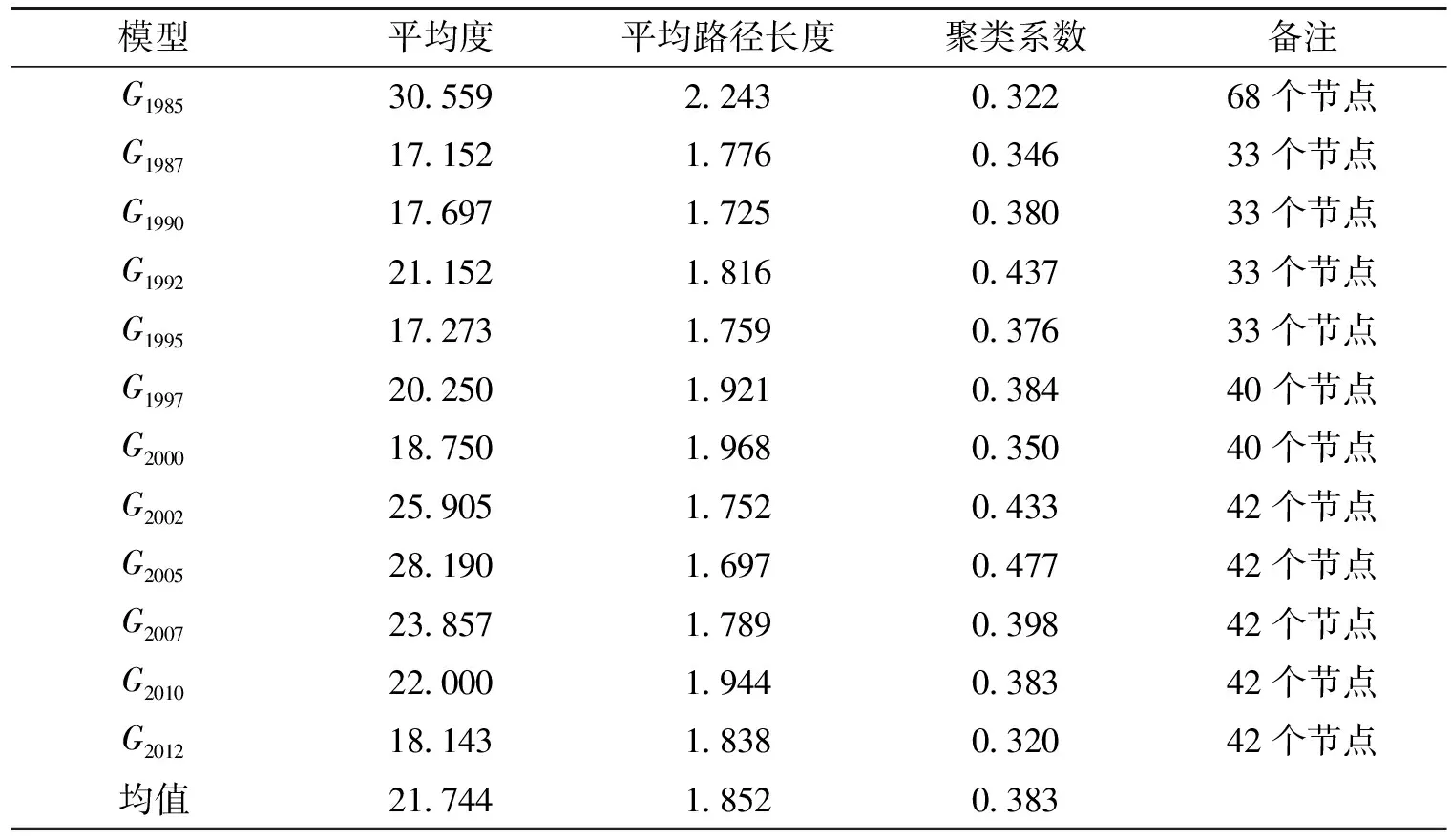
表5 模型拓撲特征演變情況

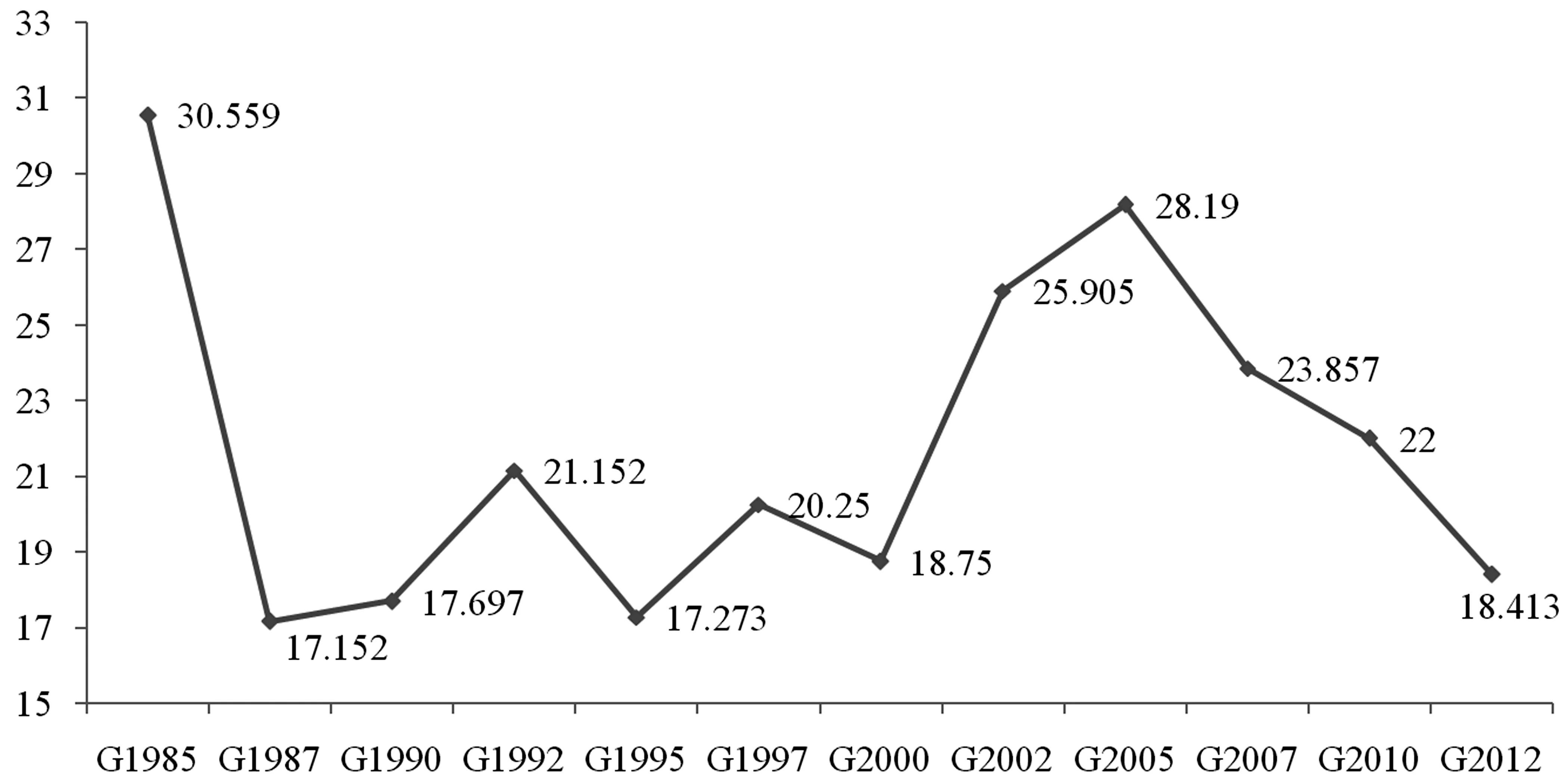
圖2 北京產業關聯網絡平均度演變情況

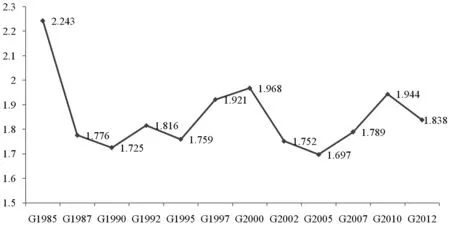
圖3 北京產業關聯網絡平均路徑長度演變情況

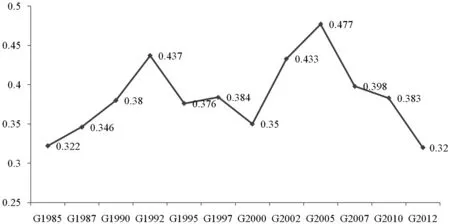
圖4 北京產業關聯網絡聚類系數演變情況

(三)對于拓撲特征演變的解釋

根據定義，平均度反映的是網絡中節點的平均聯系強度。因此，產業關聯網絡的平均度代表了不同產業部類(節點)之間的顯著聯系程度。從圖2可以發現，北京產業關聯網絡的平均度經歷了一個“降低—增高—降低”的“W”形趨勢。1985年，北京產業關聯網絡中每個產業平均與30個產業有著顯著聯系，而1995年降低到17個，隨后經歷了一定幅度的回升再降低的過程，到2012年，每個產業平均與18個產業存在著顯著的聯系，這說明北京市產業關聯整體強度呈現下降趨勢，不同產業在中間生產過程中聯系程度正在降低。

對于這種演變的一個解釋是，隨著產業經濟水平不斷升級，北京地區企業面臨的需求日益多樣化，而生產經營中的分工日益具體化，競爭強度越來越大，企業普遍追求專業化而不是范圍經濟。因此，由企業帶動的產業專業化水平逐漸提高，行業之間的顯著關聯范圍逐漸變小。

平均路徑長度代表了網絡中任意兩個節點之間距離的平均值。在產業關聯網絡中，平均路徑長度就代表任意兩個生產部類之間的間隔距離。平均路徑長度較高，表明生產部類之間的間隔就越大；反之則表示生產部類之間的間隔較小。北京市產業關聯網絡的平均路徑長度為1.851，表明任意兩個產業之間距離不超過2，即任意兩個產業之間通過1個產業就可以產生顯著聯系，具備明顯的“小世界”特性。圖3顯示，北京市產業關聯網絡的平均路徑長度經歷了一個“降低—增加—降低”的“W”形的過程，表明這十年來北京市產業內部關聯呈現出“稀疏—緊湊—稀疏”的態勢。

造成這種演變態勢的主要原因可能是北京經過承辦2008年奧運會等活動之后，城市發展水平上升到了一個新高度，經濟增長方式大幅轉變：科技創新與文化創新成為北京經濟發展的新“引擎”，文化創意產業和生產性服務業成為主導產業，總體經濟實力又得到了進一步增強。在此進程中，許多傳統行業如輕重制造業等轉移、轉型，取而代之的是人力資本含量更高的生產性服務業和文化創意產業，這些產業在生產過程中要素流通更為頻繁，第三產業集群內部的相互供給強度不斷提高，產業間的“集聚—放大—影響”的作用逐步顯現。但北京市新興產業群還處在產業周期的初級階段，產業集群雛形初現，產業帶動能力有限，集聚效應不明顯，產業聯動發展空間還比較大。

聚類系數反映的是與某一個節點連接的其他節點之間的連接程度，是考察節點之間集聚的重要指標。在產業關聯網絡中，聚類系數反映的是不同生產部類之間環向關聯的程度。產業關聯網絡的聚類系數高，表明與某一個生產部類連接的其他部類之間具有較為緊密的聯系。聚類系數低說明與某一個生產部類聯系的其他部類之間不存在緊密聯系關系。也就是說，產業關聯網絡中的環向關聯度較低，產業鏈的技術經濟聯系結構比較簡單，基本上屬于“直線型”；聚類系數高說明環向關聯緊密，產業鏈通過復雜的技術經濟聯系構成一個“環”，結構上趨于“環線型”。圖表顯示，北京市產業關聯網絡中的聚類系數經歷了一個“增加—降低—增加—降低”的“M”形過程，在2005年聚類系數達到了最大值。

究其原因，北京經濟逐步轉為外向型經濟，越來越多的生產要素和中間產品由外地供應，對區域內產業中間產品的依賴度逐漸降低，加上服務貿易和服務外包發展水平不斷提高，基礎設施建設日趨完善，物流產業發展日益加快，流通成本大大降低，這些因素均促使北京區域內的產業逐步通過北京區域外的市場為自身提供中間產品，內部環向關聯程度大大降低。

六 影響機制分析

(一)研究思路與模型選擇

為了揭示推動北京產業關聯網絡演變的核心因素，需要選擇合適的計量工具進行因果判定。從現有研究方法來看，經濟科學經驗研究中的因果判定主要有以下幾種方法：多元線性回歸(MLR)、機器學習(ML)、魯賓因果模型(Rubin’s Casual Models)、結構模型(SM)、充分統計量法(SS)等。盡管它們的具體方法和適用對象不盡相同，但本質上都是在尋找可信的對照組，利用不同控制條件下的對照組數據進行計算，進而做出因果推定。但如果變量之間沒有理論聯系，或者不存在結構支撐，則可用向量自回歸模型(Vector Auto-Regression Modle, VAR)分析數據。向量自回歸模型考慮到了數據的統計學性質，能夠更好地分析數據之間的關系。它把系統中每一個內生變量當作所有內生變量的滯后值的函數，從而將單變量自回歸模型擴展到了由多元時間序列變量組成的“向量”自回歸模型，即擴大了數據之間關系的分析能力。并且VAR模型具有很強的包容性和擴展性，如在一定的條件下，滑動平均模型和自回歸滑動平均模型也可以轉化成向量自回歸模型，因而受到越來越多研究者的青睞。

有學者利用VAR模型特點對影響因素進行了甄別。比如，蘇方林等(2010)[21]利用加權最小二乘法與向量自回歸方法，對比性地建立廣西碳排放量及影響因素間關系的實證模型，并進一步利用脈沖響應函數和方差分解探索影響系數大小和時期變化規律。羅孝玲等(2012)[22]以2001-2010年的季度數據為樣本，定量地描述了各宏觀因素對房地產價格的影響程度,并利用脈沖響應函數和方差分解分析各個因素對房地產價格的影響時滯、持續時間和作用強度。劉海兵和劉麗(2009)[23]在建立向量自回歸模型的基礎上，運用脈沖響應函數和方差分解方法對中國居民消費價格指數的影響因素作實證分析。

選擇向量自回歸模型分析產業關聯網絡演變的影響機制有以下幾點優勢：第一，嘗試深入分析影響產業關聯網絡演變的內在因素，利用VAR模型識別產業關聯網絡演變和諸多解釋變量之間的關系；第二，向量自回歸模型對結構、規模較小的數據具有良好的計量效度。本研究中數據規模有限，向量自回歸模型比較適應實際情況；第三，向量自回歸模型對數據質量的要求不是很高，可以較好地處理序列數據，而且參數的估計比較容易，這種特性保證了模型分析的信度。

(二)變量與數據來源

采用上文分析的平均度、平均路徑長度和聚類系數作為北京產業關聯網絡拓撲特征演變的變量。參考已有研究成果，通過德爾菲法獲取影響因子，選擇以下變量為北京產業關聯網絡演變的影響因素，將地區人均GDP等解釋變量引入。表6列出了各變量及其含義、數據來源與描述性統計情況。

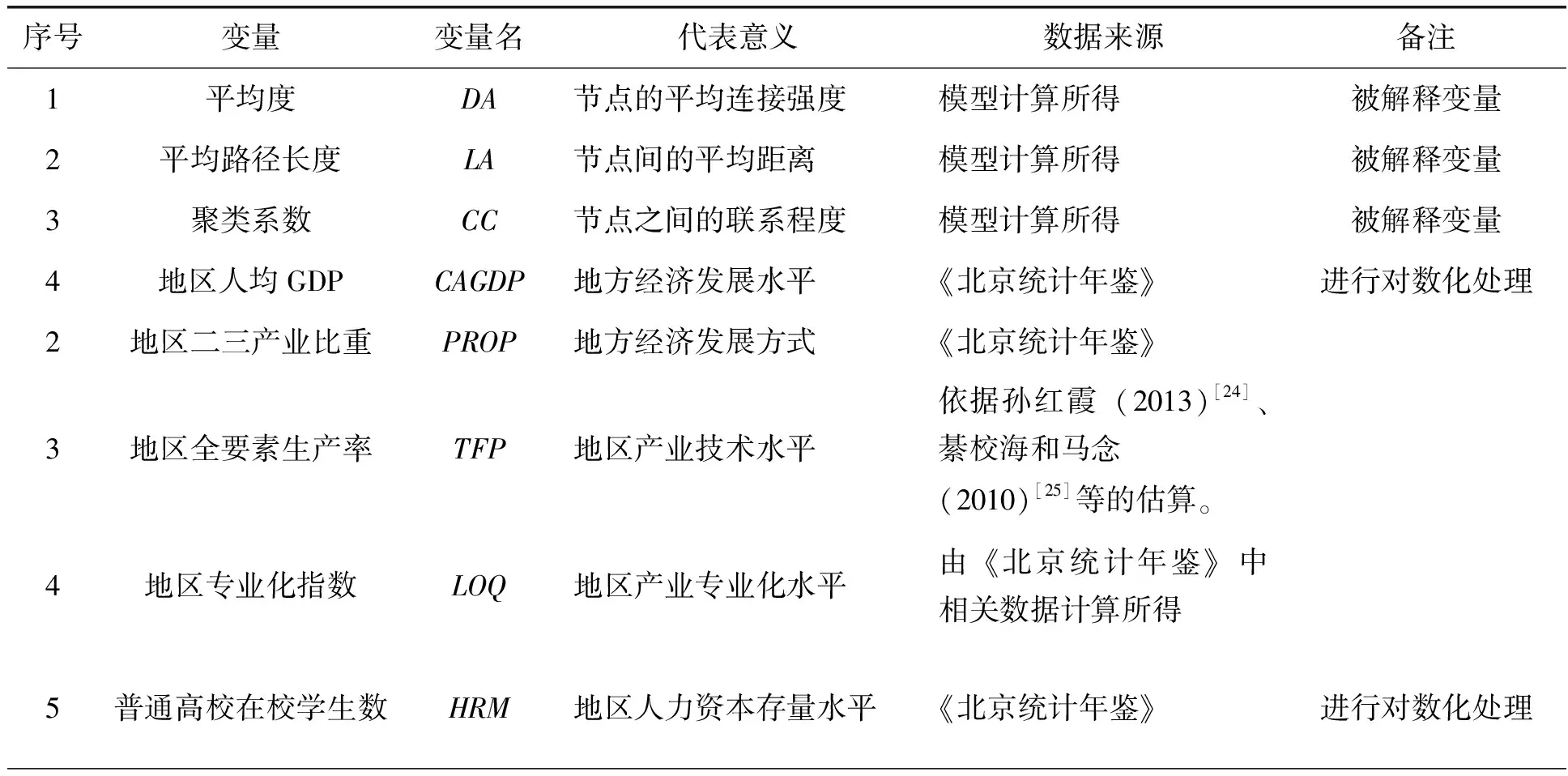
表6 變量含義與數據來源

(續上表)

序號變量變量名代表意義數據來源備注6貨運周轉量TFT反映國內貿易水平《北京統計年鑒》進行對數化處理7外貿貢獻率CRF反映地區經濟開放程度《北京統計年鑒》

注：地區專業化指數是評價地區專業化部門綜合發展程度的指標,其計算方法為:設某地區有幾個專業化部門(或生產部門),每部門占全地區產值的比重為Yi,則專業化指數:X=nY1+(n-1)Y2+(n-2)Y3+…+[n-(i-1)]Yi+…+Yn，式中Y1、Y2、…Yn按由小至大順序排列。

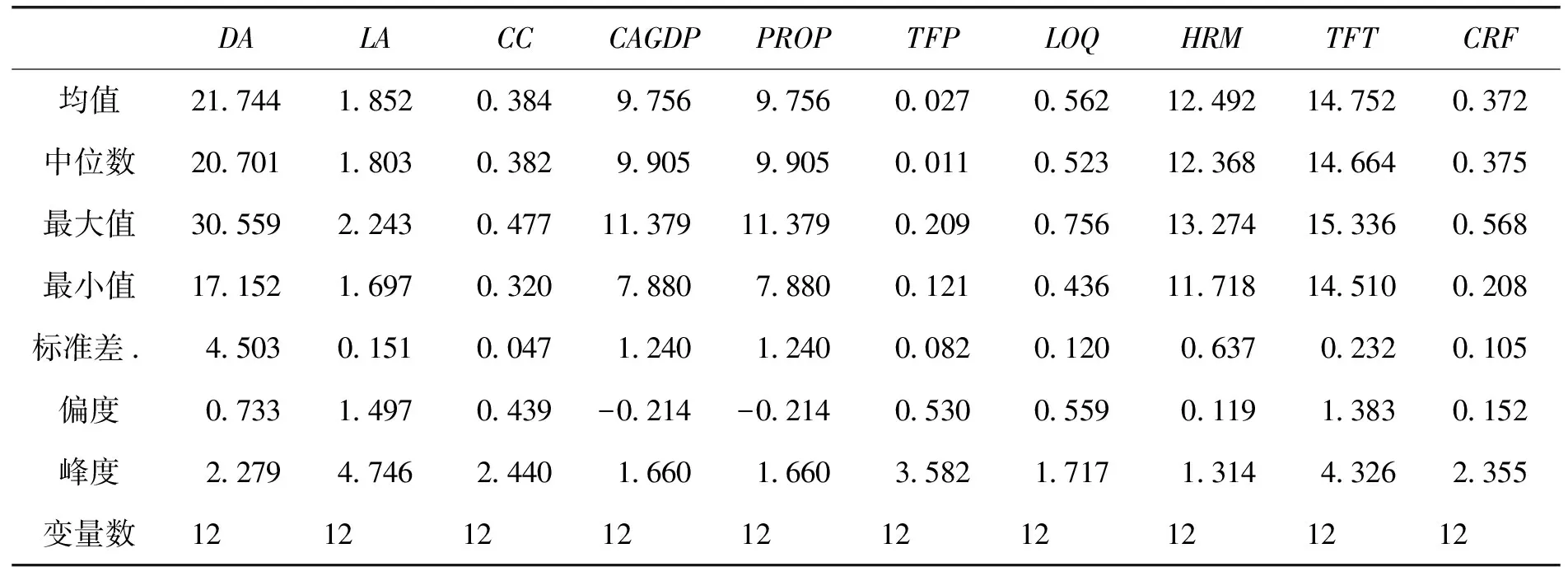
表7 變量的描述性統計情況

(三)運算過程與結果

不考慮變量的性質，先建立初步的向量自回歸模型。本文首先利用滯后階數為2的向量自回歸模型作為初步分析模型。其中，VAR1模型是包含DA、CAGDP和LOQ3個變量的向量自回歸模型；VAR2模型是包含LA、TFP、PROP和HRM4個變量的向量自回歸模型。VAR3模型是包含CC、TFT、CRT3個變量的向量自回歸模型*限于篇幅，三個向量自回歸模型的解釋式不在此列出。。

隨后，利用Eviews軟件對模型的滯后階數進行檢驗，基于AIC和SC最小化原則選擇滯后階數，最終選取滯后階數為2階，并進行格蘭杰因果檢驗。檢驗結果如下：

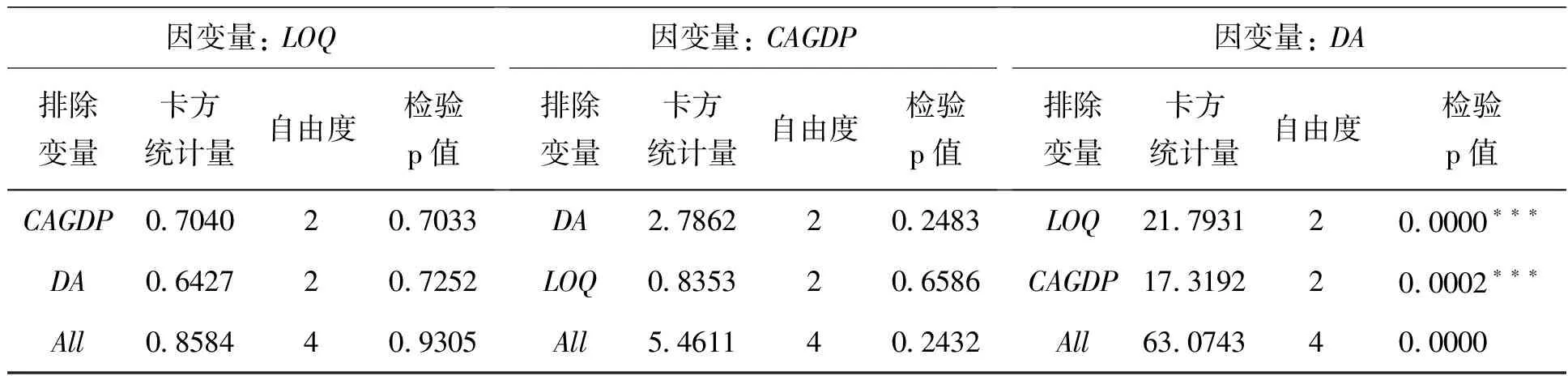
表8 VAR1模型的Granger因果檢驗結果

注：***表示在1%的顯著性水平上顯著。表9、表10同。

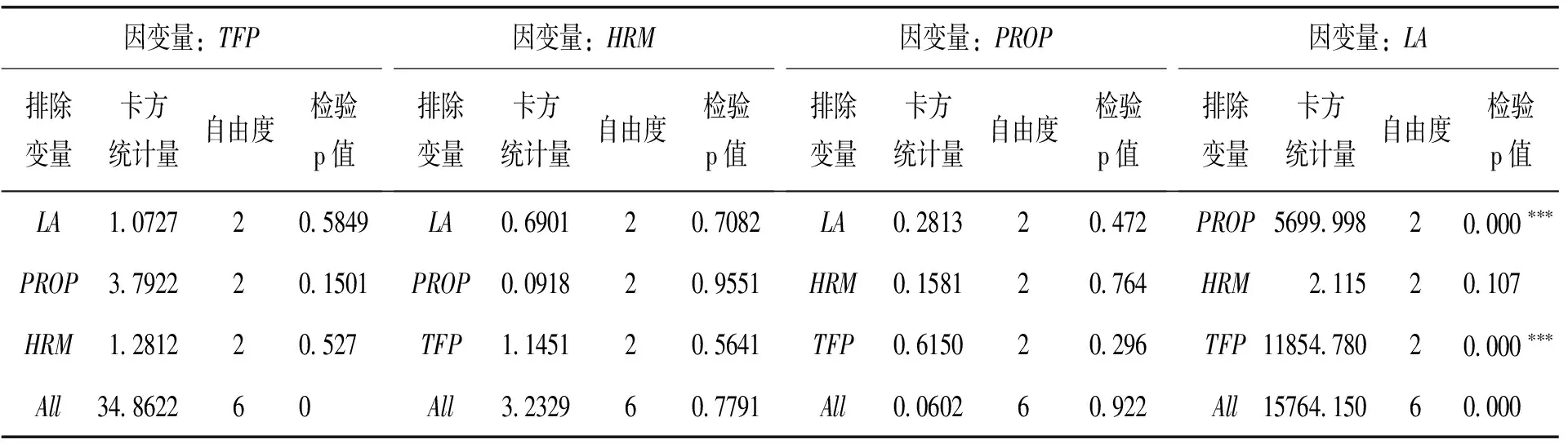
表9 VAR2模型的Granger因果檢驗結果

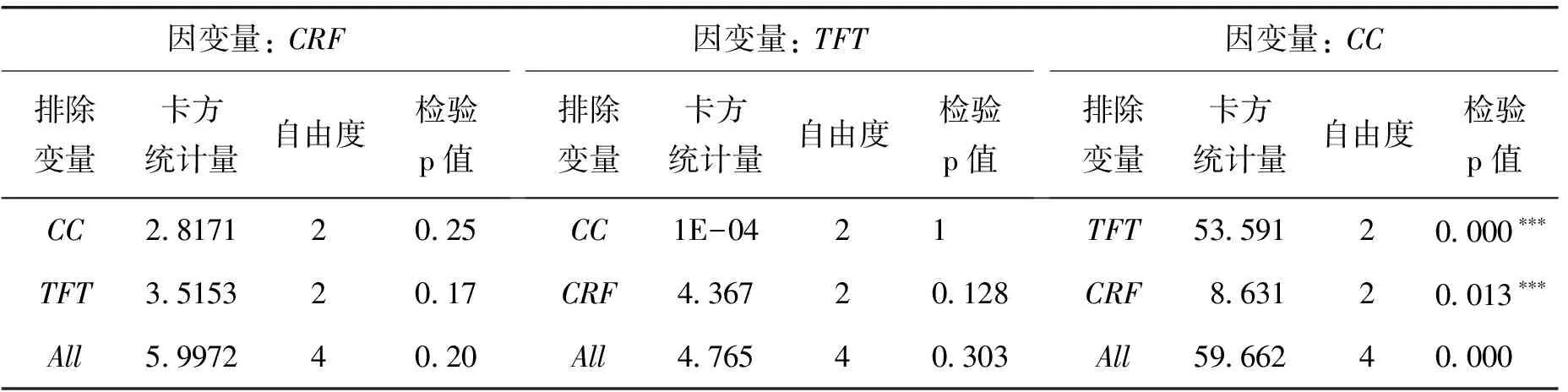
表10 VAR3模型的Granger因果檢驗結果

檢驗結果顯示，在1%的顯著性水平下，CAGDP和PROP是DA的格蘭杰原因，反之不成立；在1%的顯著性水平下，PROP、TFP是變量LA的格蘭杰原因，HRM不是變量LA的格蘭杰原因，反之不成立；在1%的顯著性水平下，TFT和CRF是變量CC的格蘭杰原因，反之不成立。

明確了各變量的滯后階數和因果關系之后，在VAR1模型、VAR2、VAR3模型的基礎上，剔除變量HRM，確立新的滯后階數，重新構建VAR1*、VAR2*和VAR3*模型。對這三個模型進行AR根檢驗發現，所有根模的倒數小于1，處在單位圓之內，說明VAR1*、VAR2*和VAR3*模型是穩定的。

以上是對影響因素的定性研究，下面利用向量自回歸模型的脈沖響應工具對影響因素的定量影響程度進行研究。脈沖響應函數分析法可以測量一個內生變量對由誤差項所帶來的沖擊的反應，即在隨機誤差項上施加一個標準差大小的沖擊后，對內生變量的當期值和未來值所產生的影響程度。本文利用這一分析技術，得到VAR1*、VAR2*和VAR3*模型的脈沖響應結果。

由圖5可以看出，當本期給CAGDP一個正沖擊后，DA在第一期的響應為負值，后在第2期轉為正值達到最高點，但沖擊程度有限(值為0.0543)；當在本期給LOQ一個沖擊后，DA會在第二期達到最高水平(值為0.0371)，然后緩慢下降。當期CAGDP的變化在第一期是反向帶動DA的變化，而在第二期后則可以同向帶動DA的變化。這表明地區經濟發展水平對于產業關聯網絡的平均度演變總體上有著正向影響，經濟發展水平越高，產業部類之間中間投入消耗強度就越大，產業關聯網絡中節點的聯系強度就越大。當期LOQ的變化在第2期后才能對DA產生正向拉動作用，這說明了地區專業化程度越高，國民經濟生產分工就越詳細，產業間聯系強度就越高。但隨著時間的推移，CAGDP和LOQ的推動作用很快轉為負值，造成這方面現象的原因可能是：隨著經濟發展水平的提高和專業化水平的提升，產業關聯網絡內部形成了一些相對獨立“聚落群類”(也就是現實中的產業群)，聚落群類內部聯系越發緊密，但產業關聯網絡整體上聯系強度卻在降低，平均度在降低。

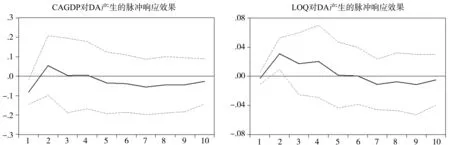
圖5 VAR1*模型的脈沖響應分析圖

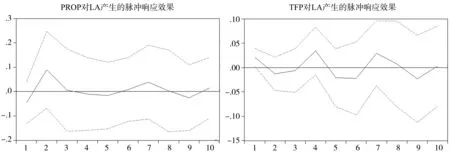
圖6 VAR2*模型的脈沖響應分析圖

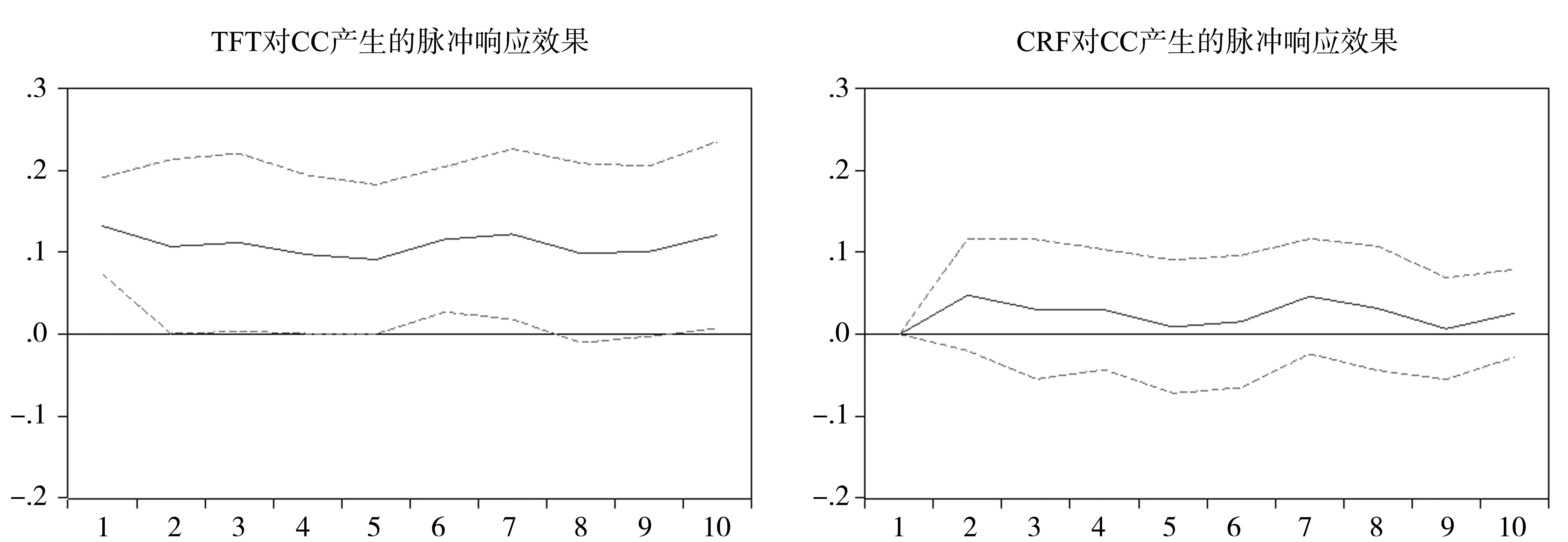
圖7 VAR3*模型的脈沖響應分析圖

由圖6可以看出，當本期給PROP一個正沖擊后，LA在第一期的響應為負值，后在第2期轉為正值并達到最高點，但沖擊程度為0.081。TFP的變化可以帶動當期LA的同向變化。但PROP和TFP在后期中的影響效果卻呈現波浪狀變化。由于PROP和TFP是代表了經濟發展方式的變量，可以嘗試得出這樣的結論：隨著經濟發展方式的轉變，整個產業關聯網絡間節點的距離正在變小，存在顯著聯系的生產部門間的聯系長度正在縮小，即“隔行不再如隔山”，但這種影響程度是隨著時間發展而起伏的。

由圖7可以看出，當本期給TFT一個正沖擊，CC在第一期的響應即為最大值(值為0.136)，而且這種影響將一直持續下去。而CRF對于CC的影響在第二期才能顯現出來，但這種影響幅度較小，平均值只有0.023左右。TFT代表的是地區國內貿易發展程度，CRF代表是地區國際貿易發展程度，可以發現：隨著北京經濟外向型程度的提高，越來越多的生產要素和中間產品由外地供應，而北京主要提供創意產品和生產指導服務，“小而全”的生產加工經濟逐步向“強而精”的總部經濟轉型，對區域內產業中間產品的依賴度逐漸降低。

七 結論與政策建議

(一)研究結論

綜合上述分析，北京市產業關聯網絡演變情況如表11所示：

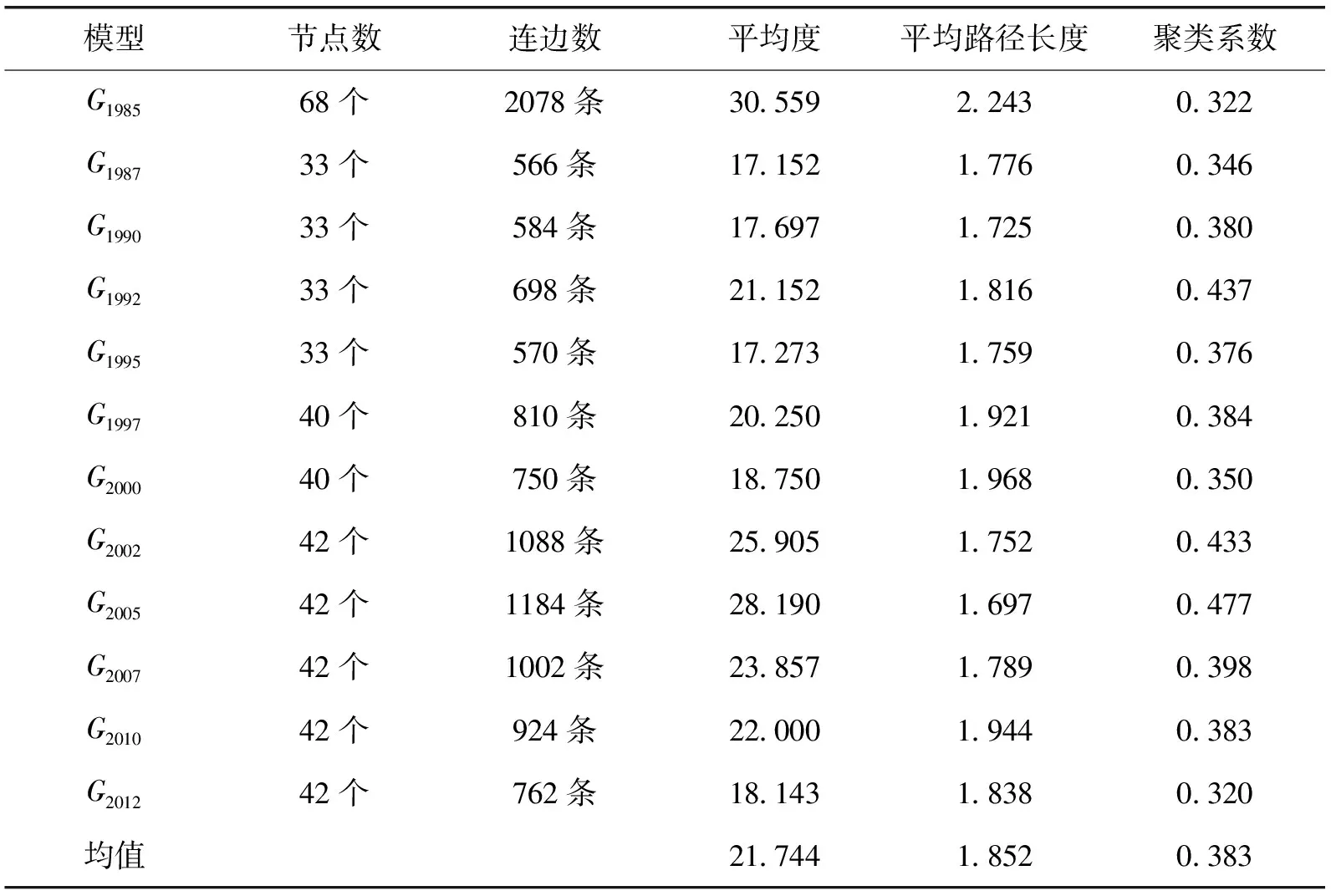
表11 北京產業關聯網絡演變情況

第一，從總體上來看，北京市產業關聯網絡的平均度呈現出“W”形變化。北京市產業關聯網絡呈現出稀疏化的發展態勢，節點之間的連邊數量不斷減少，網絡密度逐步降低。其主要原因是，北京市產業經濟的外向型程度不斷加深，對本地產業生產的中間產品的依賴度越來越低。

第二，北京市產業關聯網絡的平均路徑長度為1.852，且經歷了一個“降低—增加—降低—增加”的過程，經濟發展方式的提升對于網絡平均路徑長度產生負向影響。北京市產業關聯網絡聚類系數經歷了“M”形的變化，說明在北京產業關聯結構中直線型的關聯結構(前向關聯和后向關聯)已成為其主要結構，環向結構越來越稀疏，北京市已經形成了穩定的外向型經濟結構。

第三，進一步的影響機制研究發現，北京地區經濟總量水平和地區專業化程度負向影響網絡中節點連接強度，第三產業占比和TFP(全要素生產率)所代表的北京經濟發展方式的轉變對產業關聯網絡中的節點距離產生負向影響。地區經濟外向型水平提升造成產業關聯網絡中環向連接數量的降低，帶來網絡連接的稀疏化。

(二)政策建議

第一，觀察北京產業關聯網絡近幾年的布局，文化創意產業與生產性服務業(如文化、體育與娛樂業，信息傳輸與信息服務業、科研與技術服務業等)還處在網絡中的邊緣位置，對產業關聯的影響力有限。北京需要加強文化創意產業與生產性服務業在產業關聯網絡中的地位，發揮其價格信號傳導作用，提高北京地區人才、技術、信息的使用效率，形成重點產業群，做大做強“總部經濟”，實現京津冀產業協同發展。

第二，通過研究北京產業關聯網絡布局演變可以發現，對于處在產業關聯網絡邊緣的產業，如冶金、機械制造、服裝加工、食品加工、印刷包裝、木材加工等傳統制造業，應加大產業轉移力度。在產業轉移的過程中，應提高和增強區域產業轉移主體的市場運作能力，加強轉移出去的企業的經營體制改革，培育適應市場經濟要求的企業主體。

第三，在產業關聯網絡布局演變中，電力、熱力的生產和供應業、燃氣生產和供應業和水的生產和供應業一直處在北京產業關聯網絡的拓撲中心位置，價格傳導作用十分明顯。因此，這些行業的能源使用效率和清潔排放水平直接影響整個北京產業的能源使用效率和綠色環保水平。應提高北京市電力、燃氣和水生產供應業的技術水平和管理水平，提升能源利用效率，這是優化北京市產業能源結構的一項重要舉措，對于提高北京產業的整體能源利用效率、建設生態城市有重要意義。

[1] Leontief , W. W.. Quantitative Input and Output Relations in the Economic Systems of the United States[J].TheReviewofEconomicStatistics, 1936, 18(3): 105-125.

[2] Hayter, S.. Introduction: What Future for Industrial Relations?[J].InternationalLabourReview, 2015, 154(1): 1-4.

[3] Fang, L. C.. Chinese Industrial Relations Research: In Search of a Broader Analytical Framework and Representation[J].AsiaPacificJournalofManagement, 2014, 31(3): 875-898.

[4] Morris, H.. What’s the Point of Industrial Relations? In Defence of Critical Social Science[J].BritishJournalofIndustrialRelations, 2011, 49(49): 404-406.

[5] Erd?s, P., Rényi, A.. On Random Graphs I[J].PublicationesMathematicae, 1959, 6: 290-297.

[6] Watts, D. J., Strogatz, S. H.. Collective Dynamics of “Small-world” Networks[J].Nature, 1998, 393(6684): 440-442.

[8] Albert, R., Barabsi, A. L.. Statistical Mechanics of Complex Networks[J].ReviewofModernPhysics, 2002, 74(1): 47-97.

[9] Li, X., Jin, Y. Y., Chen, G.. Complexity and Synchronization of the World Trade Web[J].PhysicaA:StatisticalMechanicsanditsApplications, 2003, 328(1): 287-296.

[10] Campbel, J.. Application of Graph Theoretic Analysis to Inter-industry Relationships: The Example of Washington State[J].RegionalScience&UrbanEconomics, 1975, 5(1): 91-106.

[11] Slater, P. B.. The Determination of Groups of Functionally Integrated Industries in the United States Using a 1967 Inter-industry Flow Table[J].EmpiricalEconomics, 1977, 2(1): 1-9.

[12] 趙炳新. 產業關聯分析中的圖論模型及應用研究[J]. 系統工程理論與實踐, 1996, 16(2): 39-42.

[13] 方愛麗, 高齊圣, 張嗣瀛. 投入產出關聯網絡模型及其統計屬性研究[J]. 數學的實踐與認識, 2008, 38(9): 34-38.

[14] 劉剛, 郭敏. 中國宏觀經濟多部門網絡及其性質的實證研究[J]. 經濟問題， 2009, (2): 31-34.

[15] 邢李志. 基于復雜網絡理論的區域產業結構網絡模型研究[J]. 工業技術經濟, 2012, 31(2): 19-29.

[16] 侯明, 王茂軍. 北京市產業網絡結構的復雜性特征[J]. 世界地理研究, 2014, (2): 123-132.

[17] 李茂. 北京產業關聯網絡的拓撲特征研究[J]. 北京社會科學, 2016, (5): 57-67.

[18] 張許杰, 劉剛. 基于復雜網絡的英國產業結構網絡分析[J]. 商場現代化, 2008, (9): 151-152.

[19] 王茂軍, 楊雪春. 區域產業關聯網絡結構的復雜性分析——以四川省為例[R]. 中國地理學會百年慶典學術論文摘要集, 2009.

[20] Bechter, B., Brandl, B.. Measurement and Analysis of Industrial Relations Aggregates: What is the Relevant Unit of Analysis in Comparative Research?[J].EuropeanPoliticalScience, 2015, 14(4): 422-438.

[21] 蘇方林, 宋幫英, 侯曉博. 廣西碳排放量與影響因素關系的VAR實證分析[J]. 西南民族大學學報(人文社科版), 2010, 31(9): 140-144.

[22] 羅孝玲, 洪波, 馬世昌. 基于VAR模型的房地產價格影響因素研究[J]. 中南大學學報(社會科學版), 2012, 18(4): 1-7.

[23] 劉海兵, 劉麗. 基于VAR模型的CPI影響因素分析[J]. 云南財經大學學報, 2009, 25(1): 119-124.

[24] 孫紅霞. 北京地區三大產業全要素生產率的估算[J]. 現代管理科學, 2013, (10): 64-66.

[25] 綦校海, 馬念. 我國東部發達地區全要素生產率探析——基于北京、 上海1978-2008年的數據[J]. 華東經濟管理, 2010, 24(8): 51-55.

[引用方式]李茂. 產業關聯網絡演變與影響機制研究——基于北京市12個年度投入產出表的分析[J]. 產經評論, 2016, 7(6): 50-66.

The Evolution of Industrial Relations Network and the Influence Mechanism——Based on Beijing 12 Years’ Input-output Table

/2

The evolution of industrial relations network is the frontier of industried economics research. This paper constructs Beijing industrial relations network models using 12 years Beijing Input-Output table, shows the evolution of Beijing industrial relations network, calculates and compares the change in the topological characteristics of network. The paper points that the evolution of Beijing industrial relations network layout is a sparsification process, the change of the network’s average degree and the average path length exhibits a “W” shape process, the change of clustering coefficient of exhibits an “M” type process. Further analysis of the mechanism indicates that, the Beijing total economy and industry specialization negatively influences the average degree, the changes to the upgrade of economic development negatively affects the average path length, the degree of export-oriented of economy positively influences clustering coefficient. With these findings, the paper concludes with some policy suggestions for Beijing industrial economy development.

industrial relations; complex network; topological characteristics; evolution; influence mechanism

2016-08-03

北京市社會科學院2017年青年課題“京津冀地區產業關聯網絡研究”(項目編號：2016B3672，項目主持人：李茂)。

李茂，博士，北京市社會科學院市情調研中心助理研究員，研究方向為產業經濟學與技術經濟學。

F121.3

A

1674-8298(2016)06-0050-17

[責任編輯：鄭筱婷]

10.14007/j.cnki.cjpl.2016.06.005