交錯群與旗傳遞點本原非對稱2-(v,k,3)設計

王貝軍,梁洪雪,周勝林

(華南理工大學數學學院,廣東 廣州 510640)

交錯群與旗傳遞點本原非對稱2-(v,k,3)設計

王貝軍,梁洪雪,周勝林

(華南理工大學數學學院,廣東 廣州 510640)

受旗傳遞2-(v,k,3)對稱設計和非對稱2-(v,k,2)設計有關分類結果的啟發,本論文繼續研究旗傳遞非對稱2-(v,k,3)設計.文章利用置換群的理論和組合設計的數量性質,借助計算機代數軟件Gap和Magma,完全分類了自同構群G旗傳遞點本原,且基柱Soc(G)為交錯群An(n≥5)的非對稱2-(v,k,3)設計,證明了此類設計只能是唯一的2-(5,3,3)設計,且G=A5或S5.

非對稱2-設計;自同構群;旗傳遞;點本原;交錯群

1 引言

一個2-(v,k,λ)設計D為滿足下列條件的一對符號(P,B)：

(1)P是v個元素的集合,P中元素稱為點;

(2)B是P的b個k-子集的集合,B中元素稱為區組;

(3)P中任意給定的2-元子集都恰好包含在B的λ個區中.

這里我們總假定以上所有的參數皆為正整數且v＞k≥3.

若設計D的點集P上的一個置換可以誘導出區組集合B上的一個置換,則稱其為D的一個自同構.D的所有自同構的集合關于映射的合成運算構成一個群,稱為D的全自同構群,記為Aut(D).若G≤Aut(D),則稱G為D的一個自同構群.若對任意α,β∈P,存在g∈G,使得αg=β,則稱G或D是點傳遞的;若G在P上是本原的,則稱G或D點本原的;若G在旗的集合F={(α,B)|α∈B,B∈B}上傳遞,則稱G或D是旗傳遞的.若2＜k＜v-1,則設計D為非平凡的.對于2-(v,k,λ)設計來說,總有b≥v.如果b=v(等價地r=k,這里r表示過一個給定點的區組數目),那么稱D為對稱設計;如果b＞v,那么稱D為非對稱設計.

利用O’Nan-Scott定理[1],Regueiro[2]證明了2-(v,k,3)對稱設計的旗傳遞點本原自同構群是仿射的或是幾乎單的.隨后,董會莉和周勝林在文獻[3-7]中幾乎完全分類了此類設計.特別地,文獻[7]中證明了：如果D是一個非平凡的三平面,G≤Aut(D)是旗傳遞點本原的且Soc(G)=An,那么D=PG2(3,2)且G=A7或A8.

而對于非對稱的2-設計,文獻[8]證明了旗傳遞點本原且Soc(G)=An的非對稱2-(v,k,2)設計只能是2-(6,3,2)或2-(10,4,2)設計.

受到以上文章的啟發,本文對旗傳遞點本原且Soc(G)=An的非對稱2-(v,k,3)設計D進行研究,得出以下主要結論：

定理 1.1設D是一個非平凡非對稱的2-(v,k,3)設計,如果G≤Aut(D)是旗傳遞點本原的,Soc(G)=An(n≥5),則D是一個2-(5,3,3)設計且G=A5或S5.

2 準備知識

下面給出設計及其自同構群的一些基本知識.

引理2.1若D是一個非對稱的2-(v,k,λ)設計,則

(1)vr=bk;

但這并不意味著龍套就不重要，更不是可有可無。將主角與龍套的關系比喻為紅花與綠葉，很有道理。紅花固然鮮艷奪目，如果少了綠葉扶持，赤裸裸的紅花不僅顯得形單影只，甚至給人流水飄零的感覺。陪伴的綠葉如果缺乏精氣神，耷拉著、萎縮著，也給人花期將盡之感；綠葉春意盎然，紅花才能顯示勃勃生機。

(2)λ(v-1)=r(k-1);

(3)b＞v,k＜r.

引理2.2[8]設D是一個非平凡的2-(v,k,λ)設計.若G≤Aut(D)是旗傳遞點本原的,則(1)r2＞λv且|Gx|3＞λ|G|,其中Gx是點x的穩定化子;

(2)r|λ(v-1,|Gx|);

(3)r|λd,其中d為G的任一非平凡次級數.

再給出下述幾個有用的不等式.

引理2.3設s,t均為正整數.

3 定理1.1的證明

在下文中,(G,D)總是滿足下述的假設3.1.

表1 當s=2時d的取值

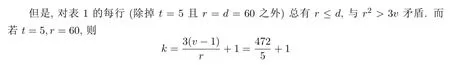
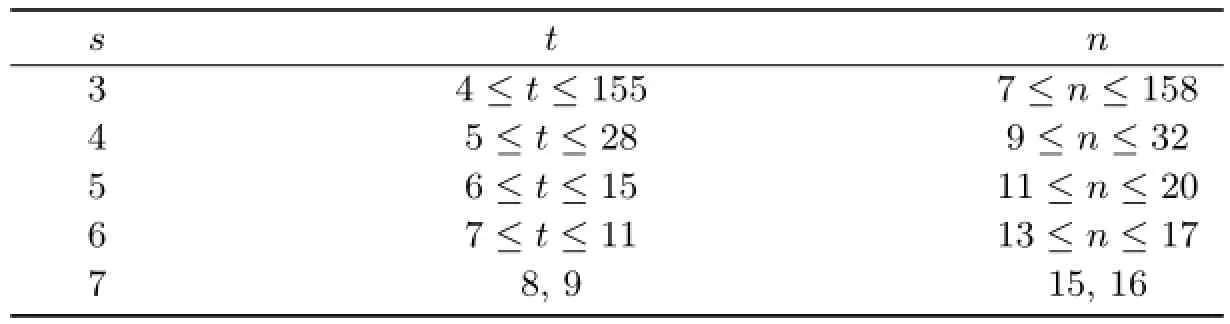
表2 當3≤s≤7時n的取值

[1]Dixon J D,Mortimer B.Permutation Groups[M].New York：Springer-Verlag,1996.

[2]Regueiro E.On primitivity and reduction for flag-transitive symmetric designs[J].J.Combin.Theory Ser.A,2005,109(1)：135-148.

[3]Dong H L,Zhou S L.Affine groups and flag-transitive triplanes[J].Sci.China,2012,55(12)：2557-2578.

[4]Zhou S L,Dong H L.Sporadic groups and flag-transitive triplanes[J].Sci.China Ser.A,2009,52(2)：394-400.

[5]Zhou S L,Dong H L.Exceptional groups of Lie type and flag-transitive triplanes[J].Sci.China Ser.A, 2010,53：447-456.

[6]Zhou S L,Dong H L,Fang W D.Finite classical groups and flag-transitive triplanes[J].Discrete Math., 2009,309(16)：5183-5195.

[7]Zhou S L,Dong H L.Alternating groups and flag-transitive triplanes[J].Des.Codes Cryptogr.,2010,57：117-126.

[8]Liang H X,Zhou S L.Flag-transitive point-primitive non-symmetric 2-(v,k,2)designs with alternating socle[J].Bull.Belg.Math.Soc.Simon Stevin,2016(6)：1-12.

[9]Wielandt H.Finite Permutation Groups[M].New York：Academic Press,1964.

[10]Zhou S L,Wang Y J.Flag-transitive non-symmetric 2-designs with(r,λ)=1 and alternating socle[J].Electronic J.Comb.,2015,22(2)：1-15.

[11]Liebeck M W,Praeger C E,Saxl J.A classification of the maximal subgroups of the finite alternating and symmetric groups[J].J.Algebra,1987,111(2)：365-383.

[12]The GAP Group.GAP-Groups,Algorithms,and Programming,Version 4.4,2006.

[13]Liebeck M W,Saxl J.The primitive permutation groups of odd degree[J].J.London Math.Soc., 1988,31(2)：250-264.

[14]Bosma W,Cannon J,Playoust C.The Magma algebra system I：The user language[J].J.Symb.Comput., 1997,24(3/4)：235-265.

[15]Delandtsheer A.Finite Flag-transitive Linear Spaces with Alternating Socle.In：Algebraic Combinatorics and Applications(G??weinstein,1999)[M].Berlin：Springer,2001：79-88.

Alternating groups and flag-transitive point-primitive non-symmetric 2-(v,k,3)designs

Wang Beijun,Liang Hongxue,Zhou Shenglin
(School of Mathematics,South China University of Technology,Guang′zhou 510640,China)

Motivated by the classification of flag-transitive 2-(v,k,3)symmetric designs and non-symmetric 2-(v,k,2)designs,this paper continue to study flag-transitive non-symmetric 2-(v,k,3)designs.We completely classify all flag-transitive point-primitive non-symmetric 2-(v,k,3)designs with alternating socle An(n≥5)by applying the theory of permutation groups,arithmetic properties of designs and the computer algebraic systems GAP and Magma,and show that there exists a unique 2-(5,3,3)design with G=A5or S5.

nonsymmetric 2-design,flag-transitive,point-primitive,alternating group

O157.1

A

1008-5513(2016)06-0649-12

10.3969/j.issn.1008-5513.2016.06.011

2016-07-31.

國家自然科學基金(11471123)

王貝軍(1990-),碩士生,研究方向：群與組合設計.

2010 MSC:05B05,05B25,20B25