帶有變指數擬線性橢圓方程組的邊界爆破解
朱瑩,馬飛遙
(寧波大學理學院,浙江 寧波 315211)
帶有變指數擬線性橢圓方程組的邊界爆破解
朱瑩,馬飛遙
(寧波大學理學院,浙江 寧波 315211)
研究了在光滑有界域中帶有變指數的擬線性橢圓方程組,且該方程組滿足邊界爆破的條件,在常指數的基礎上進一步深入討論了變指數的情況.主要運用了構造上下解和迭代的方法證明了邊界爆破解在臨界與次臨界條件下,解的存在性,唯一性以及邊界行為.
橢圓方程;擬線性;變指數;邊界爆破
1 引言
本文將研究如下帶有變指數擬線性方程組的邊界爆破問題

其中?是RN中的光滑有界域,?p代表p-Laplacian算子,定義為
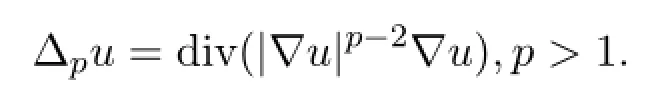
指數a(x),b(x),c(x),e(x)滿足a(x),e(x)>p-1,b(x),c(x)>0.邊界爆破行為是指當d(x)→0+時,u(x),v(x)→+∞,其中d(x)表示?中任意一點x到邊界??的距離,即
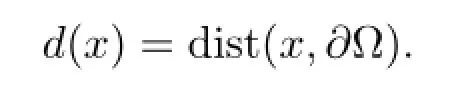
邊界爆破問題已經被大量的國內外研究者研究.他們分別從不同的角度用不同的方法研究了不同問題的邊界爆破,從單個方程到方程組,從線性方程,半線性方程,擬線性方程到完全非線性方程,研究了所謂的次臨界、臨界乃至超臨界時的邊界爆破問題.
文獻[1]在對方程 ?u=eu,x∈?,u=∞,x∈??作了探討,證明該方程具有唯一解u∈C2(?),并且給出了邊界行為.從此拉開了研究橢圓方程邊界爆破問題的序幕.
文獻[2]研究了含一般右端項的擬線性橢圓方程?pu=f(u)在右端項為單調增的正函數和一些其他的條件時的解的情況.與此同時,還研究了徑向對稱情況下的解的邊界行為.
文獻[3]考慮了當指數a(x),b(x),c(x),e(x)為常數時的擬線性橢圓方程組

分別分析了在次臨界(a(x)-p+1)(e(x)-p+1)>b(x)c(x)和臨界(a(x)-p+1)(e(x)-p+1)=b(x)c(x)條件下解的邊界爆破行為,并且給出了滿足一定條件下的解的存在性和唯一性.文獻[4]研究了帶有權函數的擬線性單個方程的邊界爆破解.
本文的主要研究內容是基于前人研究基礎上,對變指數的擬線性方程組次臨界和臨界條件給予新的定義,并得到有類似于文獻[5]中邊界爆破的結果.我們關注的是非負的弱解,即(u,v)滿足方程組(1.1),且然而,根據p-Laplacian的正則性,我們可以觀察到弱解(見文獻[6-8]),又由變指數a(x),e(x)>p-1,再利用比較原則,可以得到在?中u,v>0(見文獻[9]).
2 主要結果
本文利用類似于文獻[3]中迭代的方法,并結合上下解的構造,得到了次臨界和臨界情況下,方程組(1.1)解的邊界行為,即:
定理2.1(次臨界條件下解的存在性)假設(a(x)-p+1)(e(x)-p+1)>b(x)c(x),則方程組(1.1)至少有一個正解當僅當b(x)<e(x)-p+1,c(x)<a(x)-p+1.
定理 2.2(次臨界條件下解的邊界行為)假設 (u,v)是方程組 (1.1)的一組正解,a(x),e(x)>p-1,并且滿足則存在常數C1,C2,使得

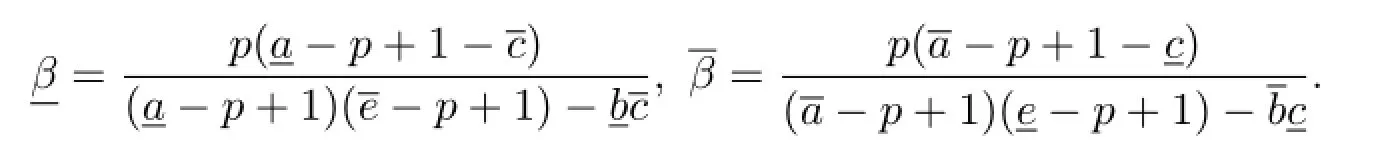
定理2.3(解的唯一性)假設(u1,v1),(u2,v2)都是方程組(1.1)的正解,a(x),e(x)>p-1,并且滿足和當x∈??時,則u1=u2,v1=v2.
定理2.4(臨界條件下解的存在性)假設(a(x)-p+1)(e(x)-p+1)=b(x)c(x),則當且僅當b(x)=e(x)-p+1,c(x)=a(x)-p+1,方程組(1.1)的解存在.
3 預備知識
在該部分,將給予本文要用到的一些新的定義并給出以下與方程組(1.1)相關的一些單個方程以及相關方程組的一系列性質.
對于q(x)>p-1,γ(x)>0,考慮方程
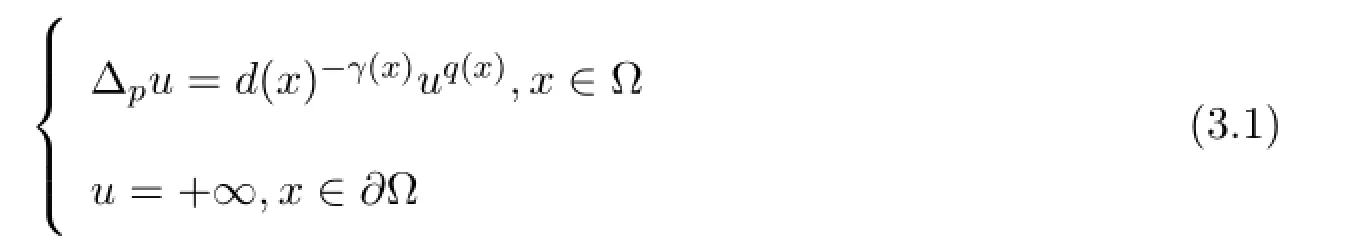
其中d(x)=dist(x,??).
定義3.1定義兩個變量
其中Uq(x),γ(x)為方程(3.1)的解.由文獻[4]可知當q(x)與γ(x)都為常數時,Aq(x),γ(x),Bq(x),γ(x)為正的且有限的變量.
定義3.2如果方程組的指數滿足條件(a(x)-p+1)(e(x)-p+1)>b(x)c(x),稱為次臨界條件;類似地,如果方程組的指數滿足(a(x)-p+1)(e(x)-p+1)=b(x)c(x)則稱為臨界條件.且定義為a(x),b(x),c(x),e(x)的最小值;為a(x),b(x),c(x),e(x)的最大值.
定義3.3如果當使得
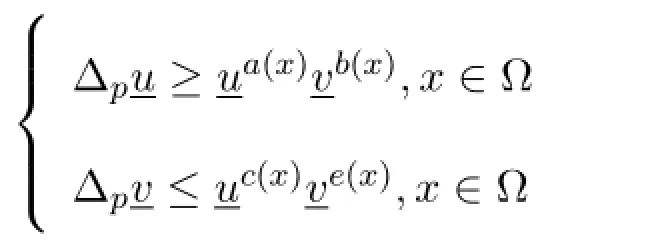
引理 3.1[10]令G:Q×R→R是連續且不增的,u,v∈W1,p(Q)對所有的非負函數分別滿足不等式

且滿足u≤v,x∈??,則u≤v,x∈?.
引理3.2假設和分別是下列方程組的下解和上解,


引理 3.3假設和分別是方程組(3.2)的下解和上解,且當當x∈?,則方程組 (3.2)至少有一個弱解 (u,v),且滿足當當x∈??,u=v=+∞.

引理 3.4令(u1,v1),(u2,v2)是下列方程組的弱解



4 定理的推論與證明
4.1 次臨界條件



4.2 臨界條件

參考文獻
[1]Bieberbach L.?u=euuud die automorphen funktionen[J].Math.Ann.,1916,77:173-212.
[2]Jerk Matero.Quasilinear elliptic equations with boundary blow-up[J].Journal d′Analyse Mathmatique, 1996,69:229-247.
[3]Meli á n J G.Large solutions for an elliptic system of quasilinear equations[J].J.Diff.Eqns.,2008,245:3735-3752.
[4]Chen Y J,Zhu Y P,Hao R Y.Large solutions with a power nonlinearity given by a variable exponent for p-Laplacian equations[J].Nonlinear Analysis,2014,110:130-140.
[5]Meli á n J G,Rossi J D.Boundary blow-up solutions to elliptic systems of competitive type[J].J.Diff.Eqns.,2004,206:156-181.
[6]Di Benedetto E.C1+αlocal regularity of weak solutions of degenerate elliptic equations[J].Nonlinear Anal., 1983,7:827-850.
[7]Lieberman G.Boundary regularity for solutions of degenerate elliptic equations[J].Nonlinear Anal., 1988,12:1203-1219.
[8]Tolksdorf P.Regularity for a more general class of quasilinear elliptic equations[J].J.Diff.Eqns.,1984,51:126-150.
[9]Vazquez J L.A strong maximum principle for some quasilinear elliptic[J].Appl.Math.Optim.,1984,12:191-202.
[10]Tolksdorf P.On the Dirichlet problem for quasilinear equations in domains with boundary points[J].Comm.Partial Differential Equation,1983,8:773-817.
Boundary blow up solution for variable exponent quasilinear elliptic systems
Zhu Ying,Ma Feiyao
(Department of Mathematics,Ningbo University,Ningbo 315211,China)
The semilinear elliptic equations with variable exponents is studied in a smooth domain,and the equation systems verifies the conditions of boundary blow-up.Upon the basis of constant exponents,this paper takes into deep considerations of the case of variable exponents and obtains the existence,uniqueness and boundary behavior of boundary blow-up solutions in the critical and subcritical condition by the construction of super-sub solutions and interation method.
elliptic systems,quasilinear,variable exponent,boundary blow up
O175.25
A
1008-5513(2016)06-0640-09
10.3969/j.issn.1008-5513.2016.06.010
2016-09-12.
國家自然科學基金(11201250).
朱瑩(1992-),碩士生,研究方向:偏微分方程.
2010 MSC:35J55

