新型恒力末端執(zhí)行機構(gòu)力學特性研究

劉海平，孫鵬飛，從 強，史文華，王耀兵

（1.北京空間飛行器總體設(shè)計部，北京 100094；2.空間智能機器人系統(tǒng)技術(shù)與應(yīng)用北京市重點實驗室，北京 100094）

新型恒力末端執(zhí)行機構(gòu)力學特性研究

劉海平1,2，孫鵬飛1,2，從 強1，史文華1，王耀兵1,2

（1.北京空間飛行器總體設(shè)計部，北京 100094；2.空間智能機器人系統(tǒng)技術(shù)與應(yīng)用北京市重點實驗室，北京 100094）

單根縱向受載變形梁與線性螺旋彈簧并聯(lián)使用，提出一種可實現(xiàn)恒力輸出的新型末端執(zhí)行機構(gòu)。分別建立了單根受載變形梁和恒力末端執(zhí)行機構(gòu)的力學模型。利用解析方法參數(shù)化分析了單根受載變形梁設(shè)計參數(shù)和線性螺旋彈簧預(yù)載荷對恒力末端執(zhí)行機構(gòu)輸出力學特性的影響。考慮恒力末端執(zhí)行機構(gòu)在未知環(huán)境精細操作過程中沖擊載荷的影響，假設(shè)受到典型半正弦沖擊載荷作用，利用四階龍格-庫塔法對恒力末端執(zhí)行機構(gòu)動力學方程進行求解。計算結(jié)果表明：單根受載變形梁的縱向預(yù)壓縮量、自由長度和線性螺旋彈簧預(yù)載荷可調(diào)整恒力機構(gòu)的輸出力幅值和有效恒力范圍；沖擊脈沖持續(xù)時間長度和系統(tǒng)阻尼可影響恒力末端執(zhí)行機構(gòu)輸出動態(tài)力的幅值和衰減時間。

振動與波；恒力；末端執(zhí)行機構(gòu)；受載變形梁；力學特性

隨著機器人技術(shù)的發(fā)展，各領(lǐng)域極端環(huán)境工況下機器人被越來越廣泛地應(yīng)用。其中，機器人在復(fù)雜未知環(huán)境中的精細操作技術(shù)始終是重點發(fā)展的關(guān)鍵技術(shù)之一。目前，針對機器人在未知環(huán)境下的精細操作技術(shù)的研究大多是通過力控制技術(shù)實現(xiàn)[1-2]，即在關(guān)節(jié)或末端執(zhí)行器上安裝力/力矩傳感器，實現(xiàn)機器人對操作力的感知，并通過力控制算法進行閉環(huán)控制。對機器人采用力控制方法解決精細操作問題可能帶來的不足，主要有如下兩點：

（1）機器人多為柔性，在其關(guān)節(jié)上布置力/力矩傳感器將進一步降低關(guān)節(jié)輸出軸的扭轉(zhuǎn)剛度和展開基頻；然而，力控制方法則希望機器人的結(jié)構(gòu)基頻越高越好；

（2）在未知環(huán)境下操作，機器人的末端執(zhí)行機構(gòu)可能會瞬時突變過載或受到碰撞沖擊作用，有可能超出力/力矩傳感器的量程，甚至有造成系統(tǒng)破壞的風險。

因此，現(xiàn)有基于力控制的機器人精細操作方式將對系統(tǒng)軟硬件、操作安全和可靠性帶來一系列問題，有必要研制一種可同時滿足精細操作和安全性可靠性要求的恒力末端執(zhí)行機構(gòu)。

近年來，在一定輸入位移條件下，可提供近似恒力/恒力矩輸出的機械式執(zhí)行機構(gòu)成為研究熱點[3-5]。相關(guān)研究主要利用優(yōu)化設(shè)計方法構(gòu)建由無預(yù)載變形薄片梁、連桿和彈簧組合體、柔性鉸鏈等不同方案組成靜態(tài)載荷作用下可實現(xiàn)恒力輸出的機構(gòu)。對于動態(tài)載荷（碰撞沖擊，正弦振動）的響應(yīng)特點研究則較少涉及。

恒力執(zhí)行機構(gòu)在恒力輸出范圍內(nèi)其動態(tài)剛度近似為零，因此又可稱為零剛度或者準零剛度機構(gòu)。根據(jù)力學知識，力-位移關(guān)系曲線的斜率即為剛度值。基于薄片矩形截面梁在縱向受載達到臨界屈曲狀態(tài)時表現(xiàn)為負剛度輸出特征，并聯(lián)線性正剛度彈簧所構(gòu)建的準零剛度機構(gòu)已經(jīng)被應(yīng)用于振動防護和能量吸收等領(lǐng)域[6-13]。但是，這些研究工作主要關(guān)注在環(huán)境擾動影響下，準零剛度機構(gòu)對輸入載荷的振動抑制效果，與恒力末端執(zhí)行機構(gòu)的使用環(huán)境、安裝條件及關(guān)注的靜動態(tài)力學性能指標區(qū)別較大。

使用縱向預(yù)載變形梁作為負剛度調(diào)節(jié)元件，與線性螺旋彈簧并聯(lián)構(gòu)成恒力末端執(zhí)行機構(gòu)，并對其靜動態(tài)力學特性展開研究。首先，對單根縱向受載梁的力學特性進行數(shù)學表征，通過參數(shù)化分析對其力-位移特征展開研究；然后，對并聯(lián)線性螺旋彈簧構(gòu)成恒力末端執(zhí)行機構(gòu)的輸出特征展開研究；最后，假設(shè)恒力機構(gòu)受到半正弦沖擊載荷作用，對其載荷輸出特性進行參數(shù)化分析。相關(guān)研究成果可為后續(xù)恒力末端執(zhí)行機構(gòu)的工程應(yīng)用奠定理論基礎(chǔ)。

1 恒力末端執(zhí)行機構(gòu)

恒力末端執(zhí)行機構(gòu)設(shè)計方案的三維模型如圖1所示。主要由結(jié)構(gòu)外殼、末端接頭、單根梁、預(yù)載調(diào)整機構(gòu)和線性螺旋彈簧等組成。

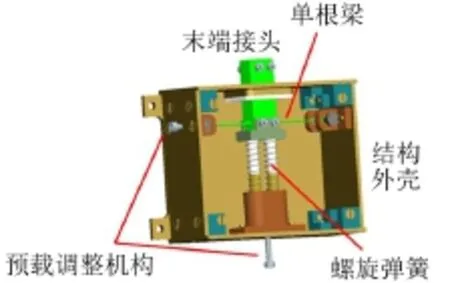
圖1 恒力末端執(zhí)行機構(gòu)三維模型（未施加預(yù)載）

2 單梁模型

單根梁受縱向載荷作用的變形如圖2所示。其中，單梁兩端固支，其縱向壓縮載荷可以由變形勢能得出。

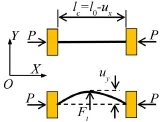
圖2 單根梁變形示意圖

構(gòu)建由無預(yù)載變形薄片梁、連桿和彈簧組合體、柔性鉸鏈等不同方案組成靜態(tài)載荷作用下可實現(xiàn)恒力輸出的機構(gòu)。

由圖2可見，假設(shè)在縱向載荷P作用下，單梁縱向受載變形量為ux。其中，l0為未受載單梁自由長度，lc為縱向受載變形梁的長度。單梁內(nèi)儲存的勢能為

其中A為矩形截面梁的截面面積，E為材料楊氏模量。

兩端固支受載變形梁的橫向變形滿足第1階模態(tài)振型的形函數(shù)

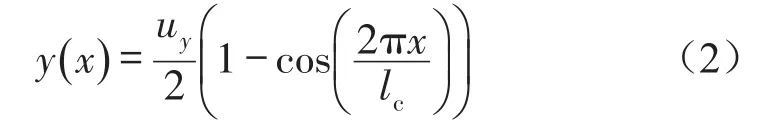
其中uy為單梁中點在橫向載荷Ft作用下的位移，x為單梁長軸方向的坐標。

縱向受載變形梁在橫向載荷作用下的長度減小量等于受載變形梁的弧長變化量。利用弧長公式，得到

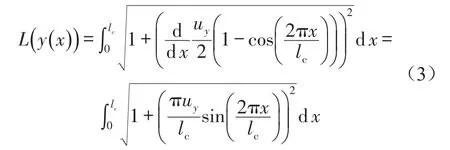
根據(jù)參考文獻[14]給出的近似計算方法，由弧長公式（3）可化簡得到弧長表達式

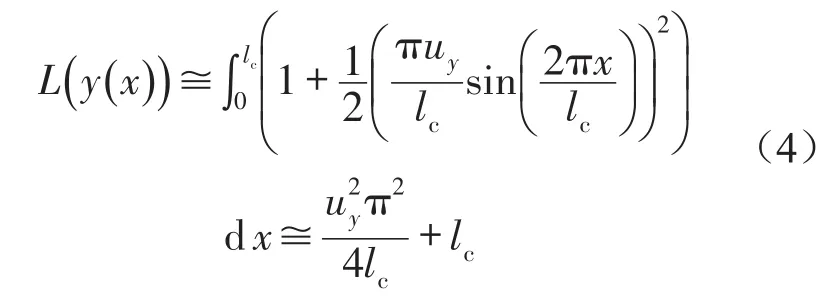
由縱向受載變形梁在橫向載荷作用下的弧長公式（4）減去縱向受載變形梁的長度lc，可以得到單梁的長度變形量。結(jié)合未受橫向載荷Ft作用時縱向受載變形梁的勢能公式（1），得到單梁內(nèi)儲存勢能的變形梁在變形過程中的勢能變化量。

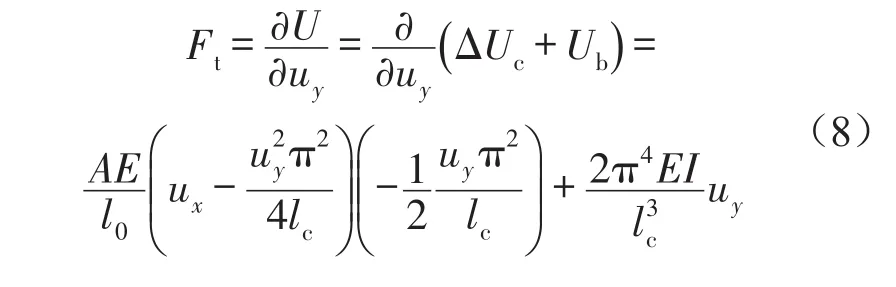
3 恒力機構(gòu)模型

單根受載變形梁在達到臨界屈曲狀態(tài)時表現(xiàn)出不穩(wěn)定的負剛度區(qū)域，為了實現(xiàn)恒力末端執(zhí)行機構(gòu)的恒力輸出特性，與線性螺旋彈簧并聯(lián)，力學模型如圖3所示。其中，F(xiàn)L為施加給末端執(zhí)行機構(gòu)的外部載荷，F(xiàn)r為預(yù)載調(diào)整機構(gòu)給恒力執(zhí)行機構(gòu)施加的預(yù)載荷，ks為線性螺旋彈簧剛度，c為阻尼系數(shù)，m為末端接頭的質(zhì)量。

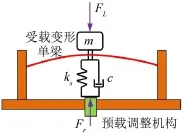
圖3 恒力末端執(zhí)行機構(gòu)示意圖

由圖3得到，縱向受載變形梁和線性螺旋彈簧并聯(lián)后的輸出合力為

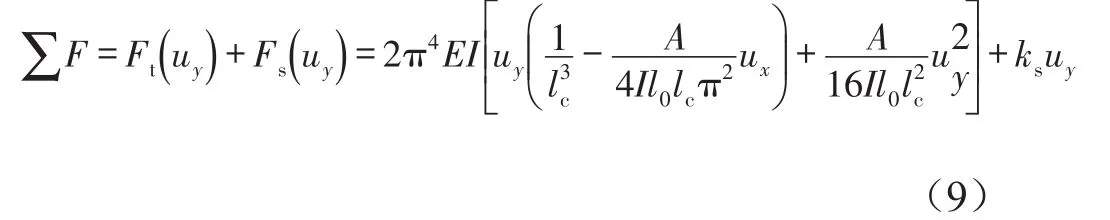
其中Ft為受載變形梁的橫向力，F(xiàn)s為線性螺旋彈簧的回復(fù)力。

根據(jù)圖3所示力學模型，得到系統(tǒng)動力學方程

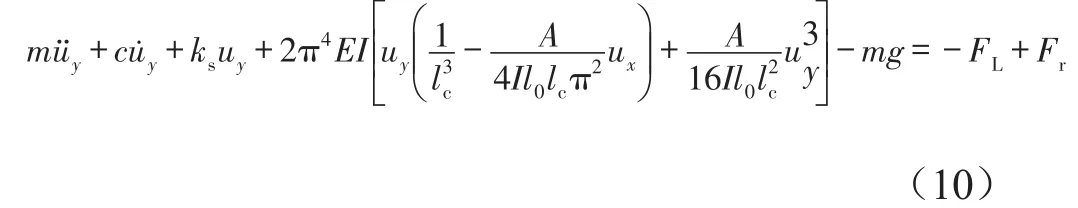
為了便于計算分析，假設(shè)y1=uy，y2=y，式（10）可化簡為常微分方程組

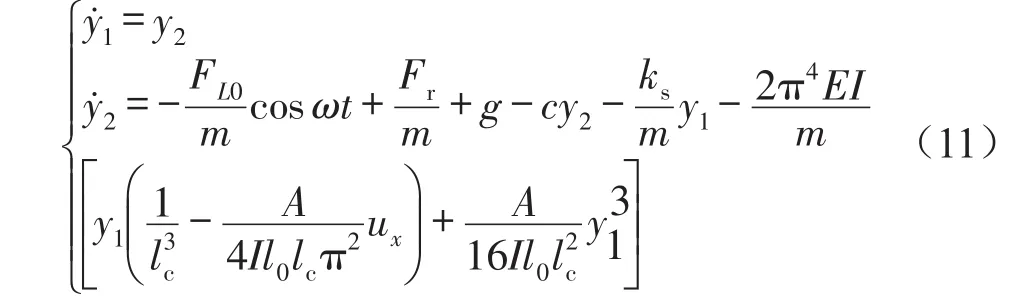
其中FL0為輸入力幅值，ω為輸入激勵圓角頻率，t為時間。

4 算例

利用以上所建靜動態(tài)力學模型，分別采用受載變形梁橫向力-位移關(guān)系的解析表達式和四階龍格-庫塔法對恒力末端執(zhí)行機構(gòu)進行參數(shù)化分析研究和力學性能評價。

為了便于后續(xù)試驗驗證，考慮利用樹脂材料，采用快速成型技術(shù)生產(chǎn)試驗件（本文暫不涉及），各設(shè)計參數(shù)詳見表1。

表1 計算參數(shù)初值

4.1 單梁靜態(tài)力學特性

利用所建立單梁靜態(tài)力-位移關(guān)系式（8），計算不同初始縱向壓縮量ux=0.1 mm、1 mm、3 mm對應(yīng)單梁橫向力-位移關(guān)系，結(jié)果如圖4所示。

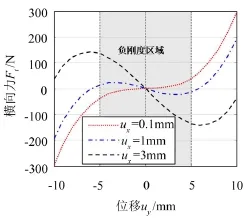
圖4 不同初始壓縮量條件下單梁橫向力-位移曲線

由圖4可見，初始壓縮量增大，受載變形梁負剛度值增大（即曲線斜率增加）；同時負剛度區(qū)域增大，參見圖中陰影區(qū)域。因此，在該陰影區(qū)域需要增加一個正剛度元件才可以使輸出總剛度為零，即實現(xiàn)恒力輸出。

圖5給出單梁自由長度變化分別取值l0=60 mm、100 mm、140 mm，對應(yīng)單梁橫向力-位移曲線。可見，隨著單梁自由長度增大，單梁負剛度值減小，而負剛度區(qū)域增大。

4.2 恒力末端執(zhí)行機構(gòu)靜態(tài)力學特性

將受載變形梁與線性螺旋彈性并聯(lián)通過剛度調(diào)節(jié)可實現(xiàn)恒力輸出，兩部分的合力參見式（9）。將表1中初始設(shè)計參數(shù)代入式（9），得到恒力末端執(zhí)行機構(gòu)的橫向力-位移曲線，如圖6所示。

圖5 不同自由長度條件下單梁橫向力-位移曲線

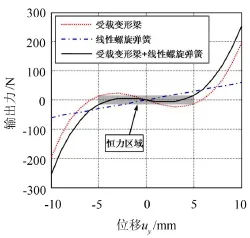
圖6 恒力末端執(zhí)行機構(gòu)橫向力-位移曲線

由圖6可見，并聯(lián)線性螺旋彈簧以后，由于疊加特性使變形梁負剛度區(qū)域變?yōu)闇柿銊偠葏^(qū)域。其中，輸出合力的變化量滿足誤差要求（一般誤差取± 10%）的區(qū)域均可認為實現(xiàn)近似恒力輸出的設(shè)計目標，參見圖6中的陰影部分。近似恒力即為輸出合力為定值，作為機器人的恒力末端機構(gòu)可保證受外部載荷作用傳遞到根部傳感器的力為定值。

實際工程中，未知環(huán)境產(chǎn)生的載荷是隨機變化的。因此，為了提高恒力末端執(zhí)行機構(gòu)的承載能力和環(huán)境適應(yīng)性，可對線性螺旋彈簧施加預(yù)載荷Fr。

假設(shè)對線性螺旋彈簧施加初始預(yù)載荷Fr=100 N，恒力末端執(zhí)行機構(gòu)的輸出力-位移關(guān)系如圖7所示。由圖可見，對線性螺旋彈簧施加預(yù)載荷使恒力末端執(zhí)行機構(gòu)的恒定輸出力區(qū)域由Ft=0附近移動到Ft=100 N附近，提高了承載能力。

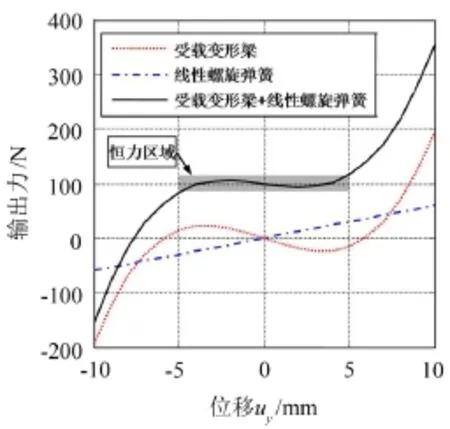
圖7 恒力末端執(zhí)行機構(gòu)橫向力-位移曲線（有預(yù)載荷）

4.3 恒力末端執(zhí)行機構(gòu)動態(tài)力學特性

恒力末端執(zhí)行機構(gòu)主要作為機器人的精細操作末端執(zhí)行單元，在未知環(huán)境下操作時在與目標物體接觸瞬間將發(fā)生碰撞，因此有沖擊載荷作用到末端執(zhí)行機構(gòu)上。為了評估恒力末端執(zhí)行機構(gòu)在瞬時沖擊載荷作用下的動態(tài)力學特性，假設(shè)輸入載荷為典型的半正弦沖擊波。

圖8給出在沖擊載荷作用下，恒力末端執(zhí)行機構(gòu)與常規(guī)線性螺旋彈簧緩沖效果的比較。其中，任取c=3 Ns/m，F(xiàn)r=100 N。由圖可見，恒力末端執(zhí)行機構(gòu)和常規(guī)線性彈簧均可對沖擊載荷產(chǎn)生緩沖效果，加速度響應(yīng)峰值衰減量均在50%以上。對比第1個加速度響應(yīng)峰值，分別為4.7 m/s2和5.1 m/s2；可見，安裝恒力末端執(zhí)行機構(gòu)可比安裝線性彈簧加速度響應(yīng)峰值減小約8%。

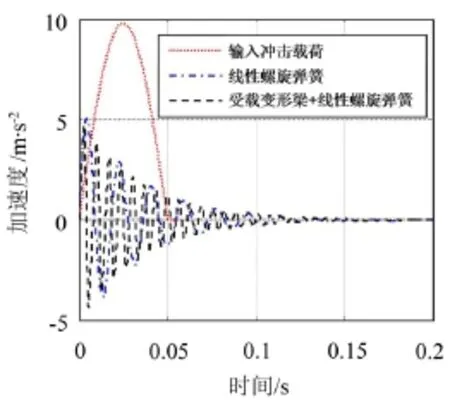
圖8 恒力末端執(zhí)行機構(gòu)抗沖擊效果曲線

圖9給出半正弦沖擊波作用下，恒力末端執(zhí)行機構(gòu)在施加預(yù)載荷Fr前后的加速度響應(yīng)。此時暫不考慮阻尼的影響，即c=0。由圖可見，沖擊載荷傳遞到恒力機構(gòu)后響應(yīng)幅值顯著降低。其中，F(xiàn)r=0 N時，加速度響應(yīng)幅值減小約為輸入加速度幅值的0.1倍；Fr=100 N時，加速度響應(yīng)幅值減小約為輸入加速度幅值的0.5倍。可見，預(yù)載荷施加前后均可以有效抑制沖擊載荷的影響。

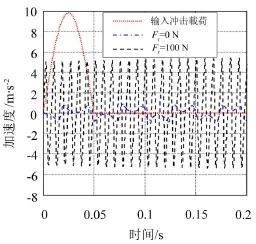
圖9 恒力末端執(zhí)行機構(gòu)加速度-時間曲線（無阻尼）

考慮系統(tǒng)阻尼（c=3 N·s·m-1）對恒力末端執(zhí)行機構(gòu)在沖擊載荷作用下動態(tài)響應(yīng)特性的影響，計算結(jié)果參見圖10。由圖可見，受阻尼影響，施加預(yù)載荷Fr前后恒力末端執(zhí)行機構(gòu)加速度響應(yīng)幅值衰減時間顯著減小，且經(jīng)過0.15 s以后，沖擊載荷引起的加速度響應(yīng)變?yōu)?。

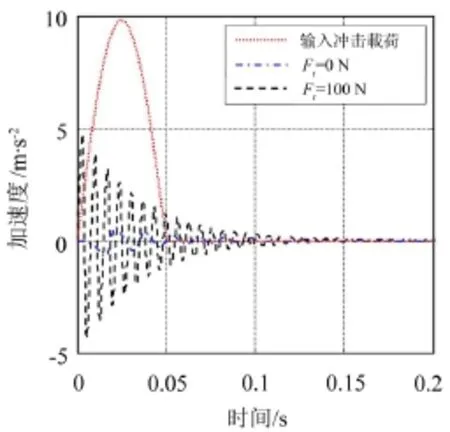
圖10 恒力末端執(zhí)行機構(gòu)加速度-時間曲線（有阻尼）

圖11給出不同沖擊時長對恒力末端執(zhí)行機構(gòu)加速度響應(yīng)的影響。圖中為了便于對比，計算結(jié)果暫不考慮阻尼對系統(tǒng)響應(yīng)的影響。可見，沖擊時長分別取τd=0.001 s、0.05 s、0.5 s時，加速度響應(yīng)幅值和相鄰響應(yīng)峰值時間間隔均減小。

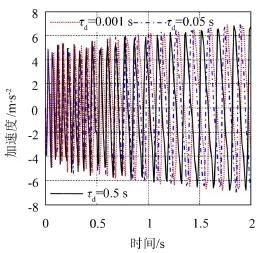
圖11 不同沖擊時長τd條件下恒力末端執(zhí)行機構(gòu)加速度-時間曲線

為了更直觀對比在動態(tài)沖擊載荷作用下恒力末端執(zhí)行機構(gòu)的輸出力特性，假設(shè)初始狀態(tài)施加預(yù)載荷Fr=100 N。利用以上計算得到的位移和加速度響應(yīng)作為輸入，求解得到輸出動態(tài)力-時間曲線參見圖12。由圖可見，不考慮系統(tǒng)阻尼的影響，c=0，受沖擊載荷作用，恒力末端執(zhí)行機構(gòu)輸出動態(tài)力隨時間變化，出現(xiàn)不同峰值的力脈沖響應(yīng)沿著輸出力幅值100 N附近上下振蕩，其中最大值約500 N。導致該現(xiàn)象出現(xiàn)的原因在于受載變形梁在負剛度區(qū)域內(nèi)波峰和波谷兩個狀態(tài)發(fā)生交替變換，參見圖4和文獻[10]。考慮系統(tǒng)阻尼的影響，分別取c=3 N·s·m-1和10 N·s·m-1，恒力末端執(zhí)行機構(gòu)輸出動態(tài)力隨著時間迅速衰減，趨于預(yù)載荷值Fr=100 N；阻尼增大，使輸出動態(tài)力趨于恒定力的時間更短，并且顯著降低了輸出力的幅值。

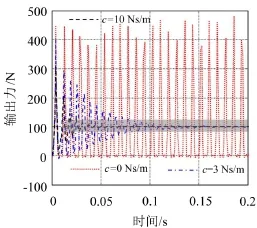
圖12 不同阻尼c條件下恒力末端執(zhí)行機構(gòu)橫向動態(tài)力-時間曲線

綜上所述，當恒力末端執(zhí)行機構(gòu)在未知環(huán)境下開展精細操作時，為了防止沖擊載荷導致的過載影響，可以通過調(diào)整受載變形梁與螺旋彈簧的組合剛度以及阻尼提供緩沖保護。

5 結(jié)語

通過縱向受載梁并聯(lián)線性螺旋彈簧，提出一種可改善現(xiàn)有機器人力控制問題的新型恒力末端執(zhí)行機構(gòu)。根據(jù)機構(gòu)的幾何構(gòu)型，分別建立單根受載變形梁和恒力末端執(zhí)行機構(gòu)的靜動態(tài)力學模型。分別采用受載變形梁橫向力-位移關(guān)系的解析表達式和四階龍格-庫塔法對恒力末端執(zhí)行機構(gòu)進行求解，參數(shù)化研究恒力末端執(zhí)行機構(gòu)在靜載和半正弦沖擊載荷作用下的力學特性。

根據(jù)計算結(jié)果，主要得到如下結(jié)論：

（1）通過調(diào)整縱向受載梁的自由長度和預(yù)壓縮量，可以調(diào)整其輸出的負剛度值和負剛度范圍；同時發(fā)現(xiàn)與線性螺旋彈簧并聯(lián)后輸出的動態(tài)力和恒力范圍也受其影響；

（2）調(diào)整恒力末端執(zhí)行機構(gòu)的動態(tài)輸出力，可通過給線性螺旋彈簧施加預(yù)載荷的方式實現(xiàn)；

（3）恒力末端執(zhí)行機構(gòu)可以抑制輸入沖擊載荷引起的加速度峰值；但是，給線性螺旋彈簧施加預(yù)載荷將使加速度響應(yīng)峰值增大。另外，沖擊載荷持續(xù)時間增加，恒力末端執(zhí)行機構(gòu)的加速度響應(yīng)幅值和相鄰響應(yīng)峰值時間間隔減小；

（4）受沖擊載荷影響，恒力末端執(zhí)行機構(gòu)的輸出動態(tài)力隨著受載變形梁在負剛度區(qū)域內(nèi)波峰和波谷兩個狀態(tài)之間交替變換，呈現(xiàn)脈沖響應(yīng)特征；且相比輸入沖擊載荷，加速度響應(yīng)得到了顯著降低；在此基礎(chǔ)上，可以通過調(diào)整恒力末端執(zhí)行機構(gòu)的系統(tǒng)阻尼進一步降低力脈沖峰值和持續(xù)時間長度；隨著時間增加，力脈沖趨近于線性螺旋彈簧的預(yù)載荷值Fr，即恒力末端執(zhí)行機構(gòu)的額定輸出力值。

研究成果可為機器人恒力末端執(zhí)行機構(gòu)的設(shè)計及工程應(yīng)用提供參考，并指導后續(xù)的試驗驗證工作。

[1]徐文福，周瑞興，孟得山.空間機器人在軌更換ORU的力/位混合控制方法[J].宇航學報，2013，34(10)：1353-1361.

[2]李大明.空間機器人在軌自主裝配動力學與控制[D].哈爾濱：哈爾濱工業(yè)大學，2012.

[3]YI HO CHEN,CHAO CHIEH LAN.An adjustable constant-force mechanism for adaptive end-effector operations[J].Journal of Mechanical Design,2012,134: 031005-1-031005-9.

[4]DHIRAJ R NAHAR,THOMAS SUGAR.Compliant constant-force mechanism with a variable output for micro/ macro applications[C].Proceedings of the 2003 IEEE International Conference on Robotics&Automation, Taipei,Taiwan,September 14-19,2003:318-323.

[5]VOLKAN PARLAKTAS.Spatial compliant constantforce mechanism[J].Mechanism and Machine Theory, 2013,67:152-165.

[6]劉海平，楊建中，羅文波，等.新型歐拉屈曲梁非線性動力吸振器的實現(xiàn)及抑振特性研究[J].振動與沖擊，2016，35(11)：155-160.

[7]劉興天，黃修長，張志誼，等.激勵幅值及載荷對準零剛度隔振器特性的研究[J].機械工程學報，2013，49(6)：89-94.

[8]JINQIU,JEFFERYHLANG,ALEXANDERH SLOCUM.A curved-beam bistable mechanism[J].Journal of Microelectromechanical Systems,2004,13 (2):137-145.

[9]GREGORY L HOIST,GREGORY H TEICHERT,BRIAN D JENSEN.Modeling and experiments of buckling modes and deflection of fixed-guided beams in compliant mechanisms[J].Journal of Mechanical Design,2011, 133:051002-1-051002-10.

[10]BENJAMIN A FULCHER,DAVIDWSHAHAN, MICHAELR HABERMAN,et.al.Analyticaland experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems[J].Journal of Vibration and Acoustics,2014, 136:031009-1-031009-12.

[11]MUSTAFA YALCIN,BIRCAN UZUNOGLU,ELIF ALTINTEPE,et.al.VNSA:variable negative stiffness actuation based on nonlinear deflection characteristics of buckling beams[C]. 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS), Tokyo,Japan,November 3-7,2013.

[12]殷小濤，孟再強，劉興星，等.非規(guī)則彈性片高靜低動的隔振特性[J].噪聲與振動控制，2013，33(6)：45-48.

[13]胡光軍，周生通，李鴻光.一種非線性隔振器的靜力分析與實驗研究[J].噪聲與振動控制，2011，31(6)：69-71.

[14]VANGBO M.An analytical analysis of a compressed bistable buckled beam[J].Sens.Actuators A,1998,69(3): 212-216.

Study on the Mechanical Characteristics of a Novel Constant-force End Effector

LIU Hai-ping1,2,SUN Peng-fei1,2,CONG Qiang1, SHI Wen-hua1,WANG Yao-bing1,2
(1.Beijing Institute of Spacecraft System Engineering,Beijing 100094,China; 2.Beijing Key Laboratory of Intelligent Space Robotic Systems Technology andApplications, Beijing 100094,China)

Using parallel connection of an axially compressed beam and a linear spring,a novel constant-force end effector is presented.First of all,a transverse force-displacement relationship for the axially compressed beam is derived. Then,a combined dynamic model including the axially compressed beam,the linear spring and a damper,is built.Finally, based on the dynamic model,the influence of some key design parameters on the performance of the constant-force end effector is studied.It is assumed that the constant-force end effector is excited by a typical semi-sinusoidal impact load when it operating in an unknown environment.Then the dynamic equations of the constant-force end effector are solved by using fourth-order Runge-Kutta method.The numerical results exhibit that the value of the output amplitude and the available range of the constant force can be adjusted by changing the values of the axial compression load and the free length of the beam.In addition,the compressive force for the linear spring also can exert some effect on the dynamic performance of the constant-force end effector.The duration of impact pulse and the system damping can also influence the amplitude of the dynamic output force and the attenuation time for the responses of the constant-force end effector.

vibration and wave;constant force;end effector;axially compressed beam;mechanical characteristics

TH113.1；O328；V231.92

：A

：10.3969/j.issn.1006-1335.2016.06.006

1006-1355(2016)06-0026-06

2016-05-31

國家自然科學基金資助項目（51405014）；總體設(shè)計部青年創(chuàng)新發(fā)展基金

劉海平（1982-），男，山西省呂梁市人，博士，高級工程師，主要研究方向為機械結(jié)構(gòu)振動噪聲控制。E-mail:lhpvibration@163.com