2PRS-2PSS并聯機構的設計與運動學分析

張彥斌 丁 丁 吳 鑫 王增輝 趙浥夫

河南科技大學，洛陽，471003

?

2PRS-2PSS并聯機構的設計與運動學分析

張彥斌 丁 丁 吳 鑫 王增輝 趙浥夫

河南科技大學，洛陽，471003

設計出一種兩移動兩轉動的四自由度2PRS-2PSS并聯機構。以該機構的4條分支運動鏈的主動移動副軸線與靜平臺的夾角為變量。首先根據方位特征集理論分析了該并聯機構的運動輸出特性；再基于矢量法對其運動學進行分析，推導出機構的位置和姿態的正解、逆解，進而推導出其速度和加速度方程；然后基于機構雅可比矩陣的奇異性，詳細討論了機構可能存在的奇異位形；最后，通過算例仿真驗證了理論分析的正確性。

并聯機構；自由度；運動學分析；奇異性

0 引言

近年來，并聯機構的應用越來越廣泛，但多數情況下不需要全部的6個自由度，因此設計滿足使用要求的少自由度并聯機構成了本領域的研究熱點[1-4]。在實際應用中，往往根據不同的工作需求選擇相應自由度類型的并聯機構，例如具有3個自由度的DELTA[5]機器人已在包裝、醫藥工業上廣泛應用，而五自由度并聯機構多用在數控加工中心[6]。空間四自由度并聯機構是少自由度并聯機構中的一個重要分支，根據動平臺運動輸出特性的不同，四自由度并聯機構可以劃分為3種類型，即三移動一轉動型[7](3T1R)、一移動三轉動型[8](1T3R)、二移動二轉動型(2T2R)。空間2T2R型并聯機構同時具有2個移動自由度和2個轉動自由度，能夠完成較為復雜的動作，已有不少學者對此類機構進行研究[9-10]。馬履中等[11]設計出一種基于2T2R型并聯機構的減振裝置，劉劍敏等[12]提出一種基于2T2R型并聯機構的振動篩，但文獻[11-12]中的機構均含有一個混合運動鏈，增加了機構的裝配難度。Kumar等[13]設計出一種可用于醫用注射的2T2R并聯機構裝置，其機構結構為3-5R，其中的一條鏈中有2個主動副，故必有1個驅動器不能安裝在機架，增加了機構的轉動慣量。范彩霞等[14]根據構型演變和李群理論綜合出一類2T2R型并聯機構。

上述文獻中所提到機構的裝配構型具有單一性，所建立的運動數學模型無法解決某一類機構的問題。因此本文提出一類2T2R型四自由度2PRS-2PSS并聯機構，推導出該并聯機構的運動學方程(位置、姿態、速度和加速度)，詳細討論了機構可能存在的奇異位形，并進行了基于虛擬樣機和理論編程的仿真，驗證了理論分析的正確性。

1 結構設計

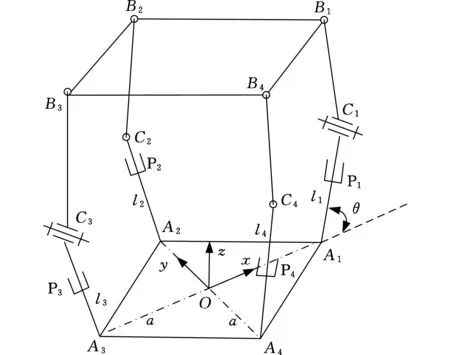
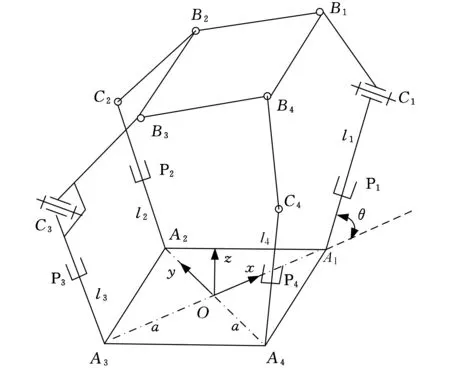
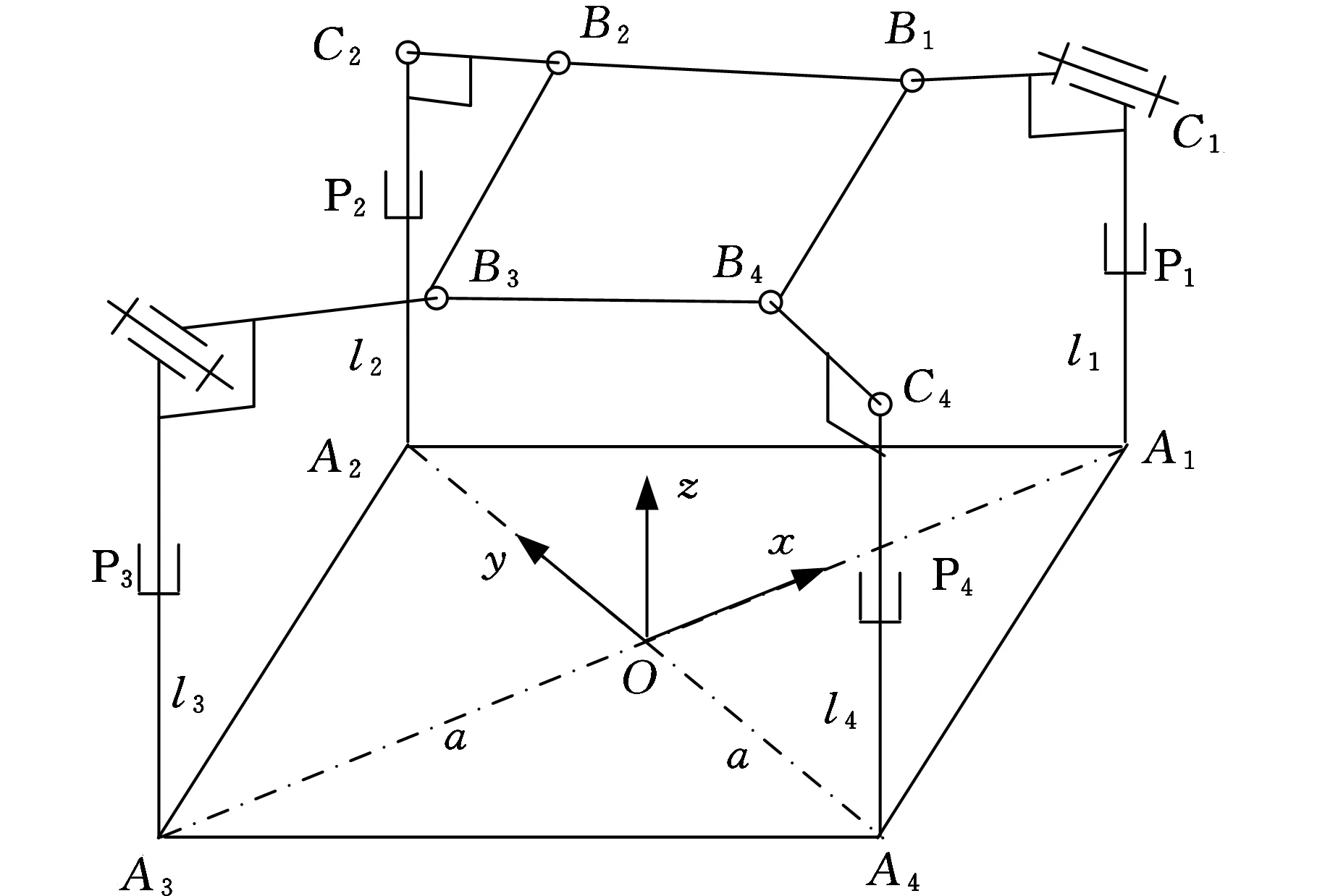
如圖1所示，新型四自由度并聯機構由動平臺、靜平臺，以及連接兩平臺的4條運動支鏈組成，機構的三維CAD模型如圖2所示。支鏈一(A1C1B1)和支鏈三(A3C3B3)的結構相同，均由移動副、轉動副和球副依次連接而成，且同一支鏈內移動副與轉動副的軸線相互垂直，記為{P⊥R-S}，同時，支鏈一和支鏈三中的2個轉動副軸線相互平行。支鏈二(A2C2B2)與支鏈四(A4C4B4)的結構也相同，從靜平臺到動平臺運動副配置依次為移動副、球副和球副，記為{P-S-S}。機構的動平臺為正方形平板B1B2B3B4，4條支鏈末端的球副分別安裝于動平臺上的Bi(i=1，2，3，4)點，4個移動副的軌道與靜平臺相交于Ai點，4個交點的連線構成正方形A1A2A3A4。機構4個主動移動副的軌道中心線與靜平臺夾角(變量)為θ。θ取不同值時，對應2PRS-2PSS并聯機構的特定裝配形式。盡管這些裝配形式下的機構運動特性不盡相同，但它們卻具有統一的運動學方程。因此，該并聯機構的設計和運動學分析適用于一類2PRS-2PSS機構，具有廣義性和普遍意義。

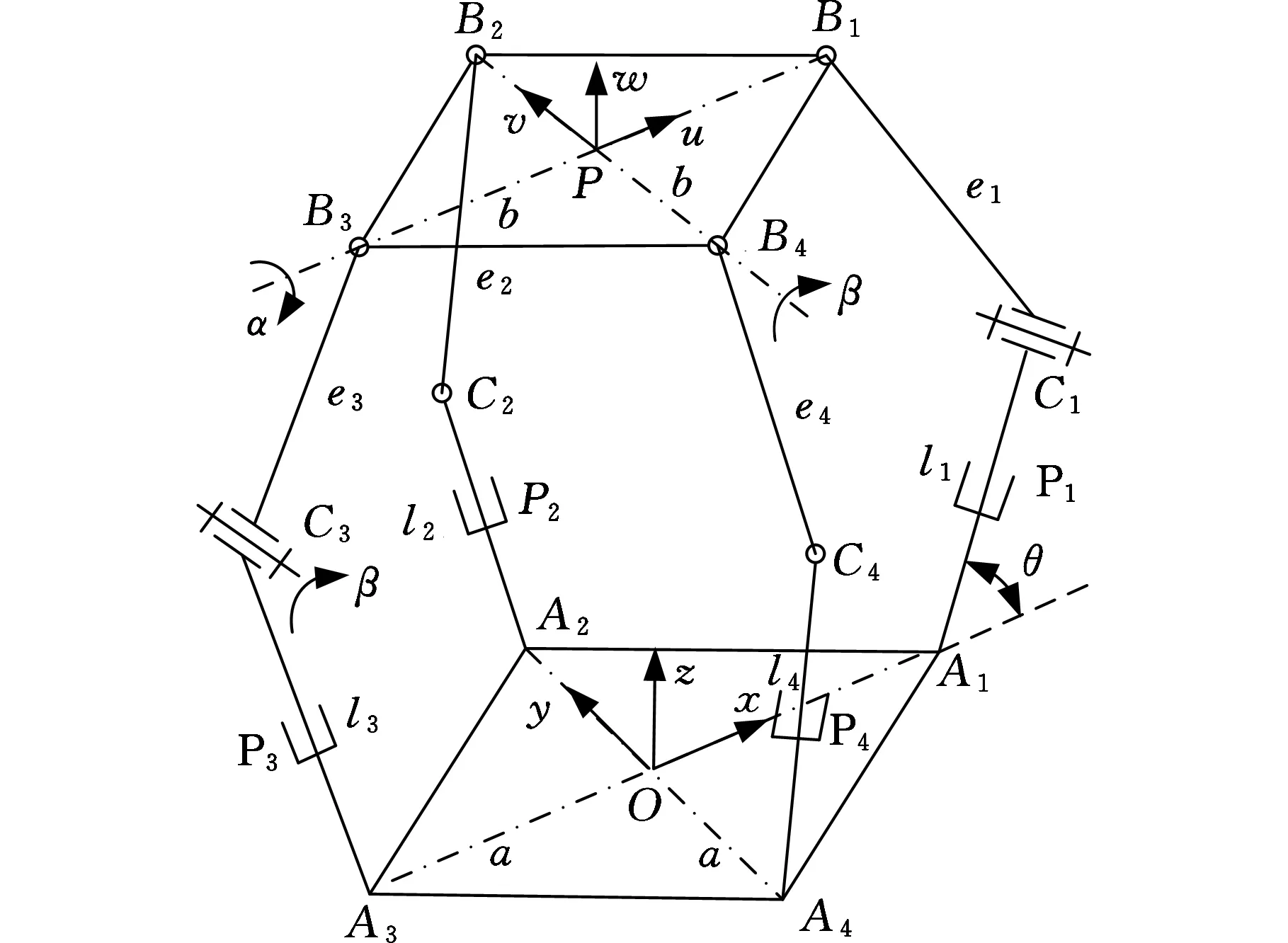
圖1 新型四自由度并聯機構

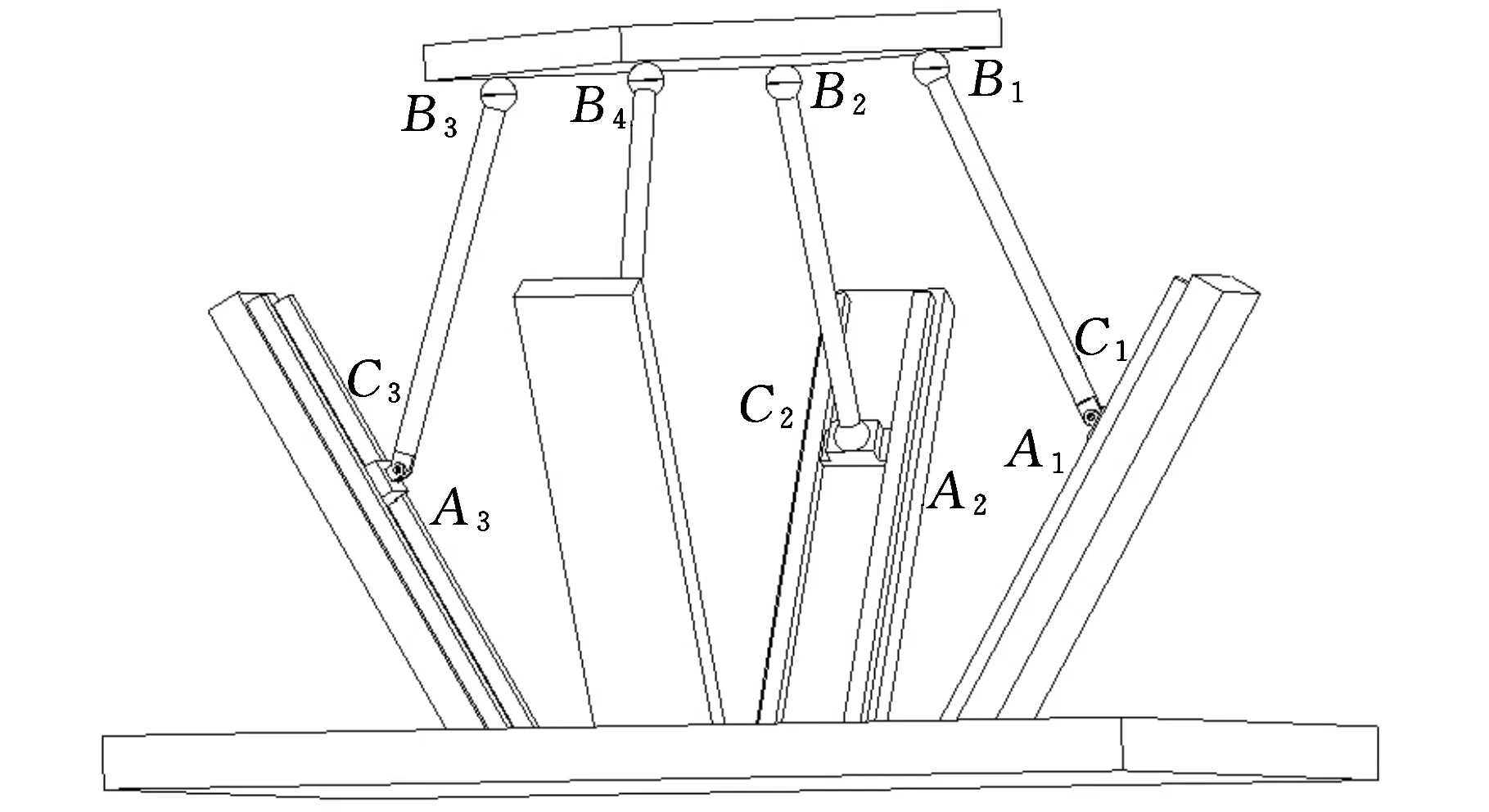
圖2 并聯機構的CAD模型

2 機構運動輸出特性分析

方位特征集法[15]是分析并聯機構的一種簡單而有效的方法，本文采用該方法對機構的運動輸出特性進行分析。

根據圖1所示機構4條支鏈的運動副配置關系，可得支鏈一與支鏈三，支鏈二與支鏈四的拓撲結構：

SOC{-Pj1⊥Rj2-Sj3} (j=1, 3)

(1)

SOC{-Pk1-Rk2-Sk3}(k=2, 4)

(2)

按照機構裝配條件，支鏈一與支鏈三、支鏈二與支鏈四末端的方位特征集分別為

(3)

(4)

其中，左下標數字表示支鏈的特征自由度數；t、r分別表示移動、轉動。如2t(⊥R12)表示垂直于R12軸線方向的2個移動自由度，1r(//Ri2)表示支鏈在平行于Ri2軸線的方向存在1個非獨立的轉動自由度。Oi3表示第i條支鏈與動平臺連接的球副的球心。連接B1B3、A1A3，如果將A1A3看作是固定機架，B1B3看作是連桿，則A1C1B1B3C3A3可視為平面六桿機構，故該六桿機構的輸出桿件B1B3只能做三自由度平面運動。但由于連桿B1B3兩端的B1和B3位置處均為球副，所以連桿B1B3繞其軸線方向存在1個局部轉動自由度。因此支鏈一與支鏈三組成的子并聯機構的方位特征集為

(5)

同理，由支鏈二和支鏈四組成的子并聯機構的方位特征集為

(6)

由于并聯機構動平臺的運動輸出特性是所有支鏈運動輸出特性的交集，所以該并聯機構動平臺的方位特征集為

(7)

式(7)表明動平臺具有2個移動自由度和2個轉動自由度，即該機構為2T2R四自由度并聯機構。

3 運動學分析

如圖1所示，定坐標系Oxyz固結在靜平臺上，坐標原點O與正方形A1A2A3A4的形心重合，x軸、y軸分別與對角線A1A3和A2A4共線，z軸垂直于靜平臺向上。動坐標系Puvw則固結于動平臺上，坐標原點P與正方形B1B2B3B4的形心重合，u軸、v軸分別與對角線B1B3和B2B4重合，w軸垂直于動平臺向上。機構在初始位置時，動平臺處于水平位置，兩坐標系的坐標軸分別對應平行。令OA1=OA2=OA3=OA4=a，PB1=PB2=PB3=PB4=b，連桿CiBi長度為ei，主動移動副位移為li。β、α分別為動平臺相對靜平臺繞定坐標系y軸和繞動坐標系u軸轉動的姿態角。

3.1 位姿分析

3.1.1 位姿逆解

對于圖1所示機構，其位姿逆解就是給定動平臺上點P的位置坐標P=(Px,Py,Pz)及動平臺的姿態角α和β，求其各驅動滑塊的位移li。

由于該機構中的閉回路A1C1B1B3C3A3可視為平面六桿機構，故動系坐標的原點P沿y軸方向的位移始終為零，因此點P在靜坐標系下的位置坐標為(Px, 0,Pz)。令R為動系Puvw相對于靜系Oxyz的姿態變換矩陣，則有

(8)

(9)

(10)

式中，Rx′為動平臺繞u軸旋轉α的變換矩陣；Ry′為動平臺繞y軸旋轉β的變換矩陣。

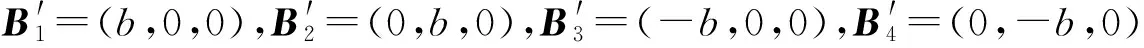
若OBi代表Bi點在靜坐標系下的坐標，則有

(11)

為了便于建立機構的矢量運動方程，可將圖1所示并聯機構的結構形式切割為圖3、圖4所示截面。圖3、圖4中，mi為滑塊移動距離AiCi的單位方向矢量，ni為連桿CiBi的單位方向矢量。根據圖3和圖4所示支鏈間的關系，可以寫出機構的閉環矢量運動方程：

OP+PBi=OAi+ACi+CiBi

(12)

將相關參數代入式(12)，得

OP+PBi=OAi+limi+eini

(13)

故有

eini=OP+PBi-OAi-limi

(14)

其中，單位方向矢量mi僅與方位角θ有關，且有m1=(cosθ，0，sinθ)，m2=(0，cosθ，sinθ)，m3=(-cosθ，0，sinθ)，m4=(0，-cosθ，sinθ)。

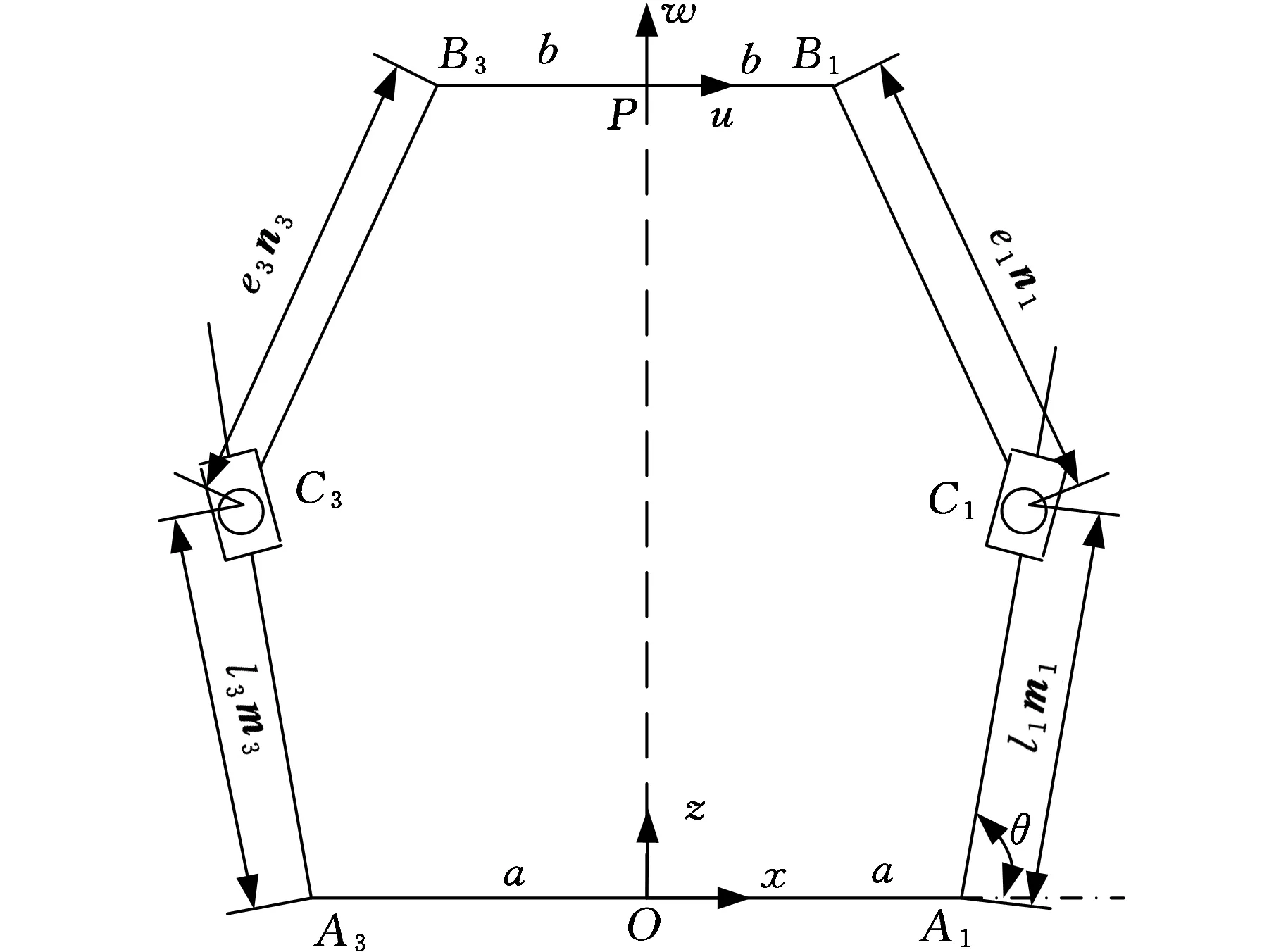
圖3 第一和第三支鏈結構簡圖

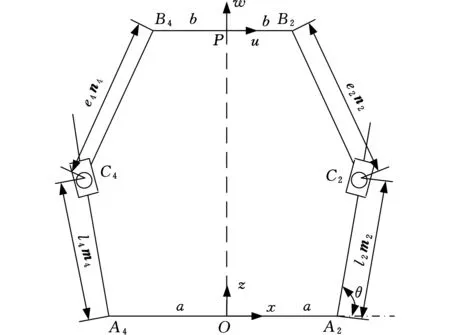
圖4 第二和第四支鏈結構簡圖

對式(14)取內積，得

(15)

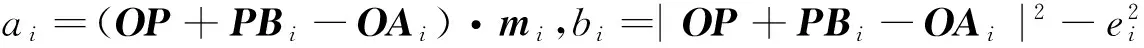
(16)

根據式(16)可求出機構的位姿逆解，即

(17)

式(17)表明機構的位姿逆解有2組，分別對應機構不同的初始裝配形式。對于圖1所示機構的裝配形式，式(17)中的“±”只能取“-”號。當取“+”號時，機構動平臺的位于分支中點Ci的下方。

同時，根據式(14)也可得到桿CiBi的瞬時單位方向矢量：

ni=(OP+PBi-limi-OAi)/ei

(18)

3.1.2 位姿正解

已知機構的4個主動移動副的輸入位移li，求解動平臺的位置坐標(Px，0，Pz)和姿態角α與β。根據圖3、圖4所示的幾何關系和坐標變換矩陣，可建立如下約束方程：

(19)

(20)

(21)

(22)

式(19)～式(22)為機構的位姿方程。這4個方程共同構成了復雜的四元二次非線性方程組，表明該機構具有強運動學耦合性。由于解析法求解普通非線性方程組較為困難，本文采用數值法，通過MATLAB編程和調用solve函數較為簡便地對機構進行運動學求解，詳見第5節。

3.2 速度分析

將式(13)對時間進行一階求導，得

(23)

將式(23)等號兩端同時右乘ni，得

(24)

根據矢量運算法則可知，(ωi×ni)·ni=0，因此可消去式(24)中最后一項，故有

(25)

進一步把式(25)寫成矩陣形式，則有

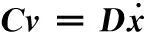
(26)

C=diag(n1·m1,n2·m2,n3·m3,n4·m4)

式(26)為該并聯機構的速度映射方程，其中，ni、PBi×ni、vp、ω均為向量。

將式(23)等號兩端同時點乘單位向量mi，可得

(27)

將式(27)進一步可得出中間變量ωi的表達式

(28)

3.3 加速度分析

將式(23)對時間進行一階求導，得

(29)

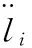
將式(29)等號兩端同時點乘單位矢量ni，則有

(30)

由式(30)可得

(31)

式(31)即為機構的加速度逆解。

4 結構奇異性

奇異性是并聯機構一個重要的內在特性，當并聯機構處于奇異位形時，其可控運動范圍和靜力平衡都會受到影響，因此奇異性分析是并聯機構設計中必不可缺少的一環。根據式(26)中矩陣C和D的欠秩形式，可將奇異類型分為逆運動學奇異、正運動學奇異和混合奇異。

4.1 逆運動學奇異

此類奇異發生在矩陣C不滿秩、矩陣D滿秩的情況下。對于圖1所示機構，根據式(26)可知矩陣C為對角陣，因此其對角線上的任意元素滿足ni·mi=0時，機構處于逆運動學奇異位形，此時方向單位矢量ni與mi正交。所以該并聯機構逆運動學奇異存在的幾何條件為，至少一條支鏈中出現連桿CiBi與移動軌道AiCi相互垂直，如圖5所示。在該位形下，即使主動移動副施加一個驅動力，由于機構的傳動角為零，動平臺也不會產生運動。

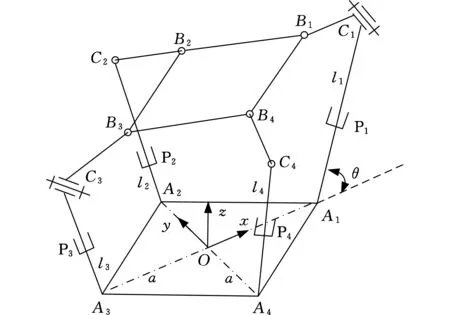
圖5 逆運動學奇異位形

4.2 正運動學奇異

此類奇異發生在矩陣C滿秩，而矩陣D不滿秩的情況下。由于式(26)中D為4×6的矩陣，所以其最大線性無關組數為4。當矩陣D不滿秩時，其行列式的秩rank(D)<4，并且4個行向量必線性相關，具體情況有以下兩種。

(1)當并聯機構的4根連桿C1B1、C2B2、C3B3、C4B4相互平行。該位形下4個單位方向矢量n1、n2、n3、n4相互平行，那么矢量PB1×n1、PB2×n2、PB3×n3、PB4×n4必共面，所以矩陣D降秩，即其行列式的秩rank(D)<4，此時機構處于奇異位形，如圖6a所示。這種奇異位形同時與機構的結構尺寸相關，一旦動平臺的邊長小于經平臺的邊長，即可避免此種奇異位形的產生。

(2)連桿C1B1與連桿C3B3共線，或者連桿C2B2與連桿C4B4共線。這種情況下PBi與ni間的夾角為0°或180°，因此有PBi×ni=0，故矩陣D的第一和第三行線性相關，或者第二和第四行線性相關。這種位形下，矩陣D同樣不滿秩，即rank(D)<4，所以機構處于奇異位形，如圖6b所示。這種奇異位形同樣與機構的結構尺寸和主動移動副的運動范圍有關，在合適的結構尺寸條件下也可避免此類奇異的發生。

(a)第(1)種情況時的奇異位形

(b)第(2)種情況時的奇異位形

當機構處于正運動學奇異位形時，動平臺將“得到”一個或者多個自由度，機構處于不可控狀態。

4.3 混合奇異

當發生此類奇異時，矩陣C和D需同時不滿秩。根據前面分析可知，若要滿足C不滿秩，至少一條支鏈中的連桿CiBi與移動軌道AiCi垂直。D不滿秩有兩種情況，滿足兩種情況對應的條件分別為θ=0°和θ=90°。所以當滿足C不滿秩和D不滿秩的任意一種情況的時候，對應的奇異位形如圖7所示。可以看出，該并聯機構處于一般裝配位形下不存在混合奇異。

(a)θ=0°時的機構奇異位形

(b)θ=90°時的機構奇異位形

5 數值算例仿真

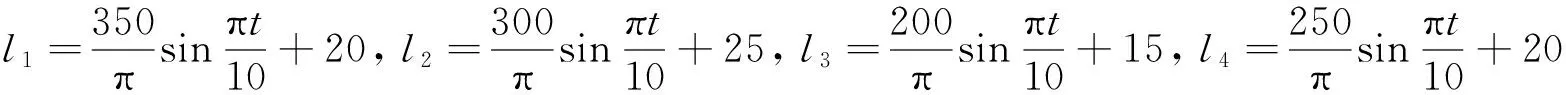
為進一步說明利用MATLAB編程調用solve函數進行非線性方程組求解的過程，以t=9 s時得到的滑塊位移為初始條件，求得動平臺上P點位姿的數值解。此時共得到機構的4組正運動學實數解(表1)，每一組實數解對應其一種裝配構型。在給定結構尺寸條件下，根據移動副的輸入范圍求出機構動平臺上點P在z軸方向的運動范圍為131.45～180.57 mm，因此可以排除第1和第3組解。而第2組解中，動平臺繞y軸的姿態角超β出了球鉸的轉角范圍，也應排除。所以只有第4組解為動平臺在此刻的可行位姿。

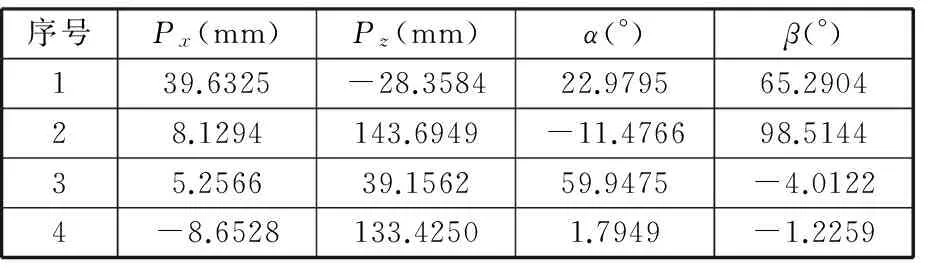
表1 機構運動學正解計算結果

最后基于所推導出的機構運動學方程，利用MATLAB對機構進行數值仿真和基于虛擬樣機的運動學仿真，如圖8所示。對比圖8中數值仿真和虛擬樣機仿真結果可知兩者結果完全一致，驗證了本文所推導理論公式(包括位姿，速度和加速度)的正確性。

6 結語

本文提出一種新型四自由度2PRS-2PSS并聯機構，因其對角分支運動鏈具有相同的拓撲結構形式，因此該機構具有較好的結構對稱性。本文分析了動平臺的運動特性，利用矢量法建立了該機構的一般運動學方程。基于所建立的運動學方程，可快速求出方位角θ取不同值時特定裝配形式下的機構的運動學解。根據機構速度雅可比矩陣，詳細分析了機構的奇異性，并給出了避免奇異位形的相關措施。通過理論編程和虛擬樣機仿真，驗證了理論分析的正確性和有效性。在后續研究中，我們將討論和研究主動關節軌道的方位角θ對該機構的工作空間和性能的影響，以便在滿足運動性能要求條件下選取機構的最佳裝配構型等。同時，在理論分析的基礎上進行實體樣機研制。

(a)位移曲線 (b)速度曲線

(c)加速度曲線 (d)角位移曲線

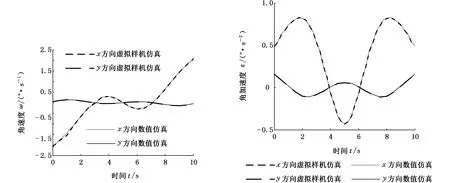
(e)角速度曲線 (f)角加速度曲線

[1] 邊輝, 劉艷輝, 梁志成, 等. 并聯2-RRR/UPRR踝關節康復機器人機構及其運動學[J]. 機器人, 2010(1):6-12. Bian Hui, Liu Yanhui, Liang Zhicheng, et al. A Novel 2-RRR/UPRR Robot Mechanism for Ankle Rehabilitation and Its Kinematics[J]. Robot, 2010 (1): 6-12.

[2] Richard P L, Gosselin C M, Kong X. Kinematic Analysis and Prototyping of a Partially Decoupled 4-DOF 3T1R Parallel Manipulator[J]. Journal of Mechanical Design, 2007, 129(6): 611-616.

[3] 竇玉超, 曾達幸, 李明洋, 等. 一種兩轉一移完全解耦并聯機器人機構及其特性分析[J]. 中國機械工程, 2014, 25(2): 241-245. Dou Yuchao, Zeng Daxing, Li Mingyang, et al. Analysis of a 2T1R Fully Decoupled Parallel Robot Mechanism and Its Characteristics[J]. China Mechanical Engineering, 2014, 25(2): 241-245.

[4] Gan D, Dai J S, Dias J, et al. Singularity-free Workspace Aimed Optimal Design of a 2T2R Parallel Mechanism for Automated Fiber Placement[J]. Journal of Mechanisms and Robotics, 2015, 7(4): 041022.

[5] Clavel R. DELTA, a Fast Robot with Parallel Geometry[C]//Proc. of the 18th International Symposium on Industrial Robots. New York, 1988:91-100.

[6] Gao F, Peng B, Zhao H, et al. A Novel 5-DOF Fully Parallel Kinematic Machine Tool[J]. The International Journal of Advanced Manufacturing Technology, 2006, 31(1/2): 201-207.

[7] Pierrot F, Company O. H4: A New Family of 4-dof Parallel Robots[C]//Proceeding of IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Atlanta, 1999: 508-513.

[8] Song Y, Gao H, Sun T, et al. Kinematic Analysis and Optimal Design of a Novel 1T3R Parallel Manipulator with an Articulated Travelling Plate[J]. Robotics and Computer-Integrated Manufacturing, 2014, 30(5): 508-516.

[9] 李永剛 宋軼民, 馮志友, 等. 4自由度非全對稱并聯機構的完整雅可比矩陣[J]. 機械工程學報, 2007, 43(6): 37-40. Li Yonggang, Song Yimin, Feng Zhiyou, et al. Complete Jacbian Matrix of a Class of Incompletely Symmetrical Parallel Mechanisms with 4-DOF[J]. Journal of Mechanical Engineering, 2007, 43(6): 37-40.

[10] Wang S. The Singularity Research of a Novel 2T2R Parallel Mechanism[C]//The Second International Conference on Mechanic Automation and Control Engineering. Hohhot, 2011: 866-869.

[11] 馬履中, 陳修祥, 楊啟志, 等. 基于并聯機構的具有冗余自由度四自由度彈性阻尼減振裝置研究[J]. 中國機械工程, 2006, 17(17): 1761-1764. Ma Lüzhong, Chen Xiuxiang, Yang Qizhi, et al. Research on 4-DOF Parallel Mechanism-Based Vibration Damping Device with Redundant Freedom[J]. China Mechanical Engineering, 2006, 17(17): 1761-1764.

[12] 劉劍敏, 馬履中, 許子紅, 等. 振動篩兩平移兩轉動并聯機構的運動學分析[J]. 農業機械學報, 2008, 39(2): 14-17. Liu Jianmin, Ma Lüzhong, Xu Zihong, et al. Kinematical Analysis of Vibrating Screen on a Kind of 2T-2R Parallel Mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(2): 14-17.

[13] Kumar N, Piccin O, Bayle B. Dimensional Synthesis of a Novel 2T2R Parallel Manipulator for Medical Applications[C]//ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. New York, 2014: V05AT08A069.

[14] 范彩霞, 劉宏昭, 張彥斌. 基于構型演變和李群理論的2T2R型四自由度并聯機構型綜合[J]. 中國機械工程, 2010, 21(9): 1101-1105. Fan Caixia, Liu Hongzhao, Zhang Yanbin. Type Synthesis of 2T2R 4-DOF Parallel Mechanism Based on Configuration Evolution and Lie Group Theory[J]. China Mechanical Engineering, 2010, 21(9): 1101-1105.

[15] 楊廷力. 機器人機構拓撲結構設計[M]. 北京: 科學出版社, 2012.

(編輯 張 洋)

Design and Kinematics Analysis of a 2PRS-2PSS Parallel Mechanism

Zhang Yanbin Ding Ding Wu Xin Wang Zenghui Zhao Yifu

Henan University of Science and Technology, Luoyang,Henan, 471003

A new two-translational and two-rotational 4-DOF 2PRS-2PSS parallel mechanism was proposed. Orientation angles among axis of all actuated prismatic joints and fixed base of the parallel mechanism were variables. Firstly, the motion output characteristics were analyzed by theory of position and orientation characteristics. The kinematics of the mechanism was analyzed by using vector approach. Forward and inverse solutions of the position and orientation of the mechanism were derived. Then, the equations of velocity and acceleration were obtained. In addition, the singular configurations of the mechanism were discussed in detail based on the singularity of its Jacobian matrices. Finally, simulation results show that the theoretic analysis is correct.

parallel mechanism; degree of freedom(DOF); kinematics analysis; singularity

2016-05-16

國家自然科學基金資助項目(50905055)；河南省高校科技創新團隊支持計劃資助項目(15IRTSTHN008)；河南科技大學重大科技項目培育基金資助項目(2015XTD012)

TH112；TP242

10.3969/j.issn.1004-132X.2016.21.004

張彥斌，男，1974年生。河南科技大學機電工程學院教授。主要研究方向為機構學與并聯機器人理論。發表論文45篇。丁 丁，男，1992年生。河南科技大學機電工程學院碩士研究生。吳 鑫，男，1957年生。河南科技大學機電工程學院教授。王增輝，男，1988年生。河南科技大學機電工程學院碩士研究生。趙浥夫，男，1988年生，河南科技大學機電工程學院碩士研究生。