時鐘數據恢復電路中的線性相位插值器

張瑤,張鴻,李梁,杜鑫,程軍

(1.西安交通大學電子與信息工程學院, 710049, 西安;2.中國電子科技集團公司第二十四研究所模擬集成電路重點實驗室, 400060, 重慶)

?

時鐘數據恢復電路中的線性相位插值器

張瑤1,張鴻1,李梁2,杜鑫1,程軍1

(1.西安交通大學電子與信息工程學院, 710049, 西安;2.中國電子科技集團公司第二十四研究所模擬集成電路重點實驗室, 400060, 重慶)

針對時鐘數據恢復電路(CDR)中相位插值器的非線性使得時鐘抖動增大的問題,提出了一種基于非等值電流源陣列的線性相位插值器。根據插值器輸出時鐘相位與尾電流權重的反函數關系,在傳統相位插值器的基礎上調整尾電流陣列中每個電流源的設計比例,并將控制管用作共柵管來提高電流源的匹配度和穩定性,從而實現了輸出時鐘相位與控制信號的線性關系,提高了CDR的調節精度并降低了恢復時鐘的抖動。采用0.25 μm CMOS工藝設計了一款基于線性相位插值器的CDR。仿真結果表明:傳統結構插值器的最大相位誤差為63.68%,而所提出的線性相位插值器的最大相位誤差僅為9.44%,可有效地降低CDR輸出時鐘的抖動。

時鐘恢復;相位插值;線性度;抖動

近年來,隨著數字系統數據傳輸速率的不斷提高,對誤碼率提出了更高的要求。在串行接口的接收端,恢復時鐘的抖動決定了恢復數據的誤碼率。在各種結構的時鐘數據恢復電路(CDR)[1]中,基于相位插值器的CDR采用數字電路實現對環路的控制和調節,節省了芯片的面積和功耗,應用十分廣泛。相位插值型CDR中,恢復時鐘的相位調節主要由相位插值器來完成。插值器的線性度越高,CDR的調節精度越高,抖動越均勻,相位鎖定時輸出時鐘的抖動越小,恢復數據的誤碼率越低。

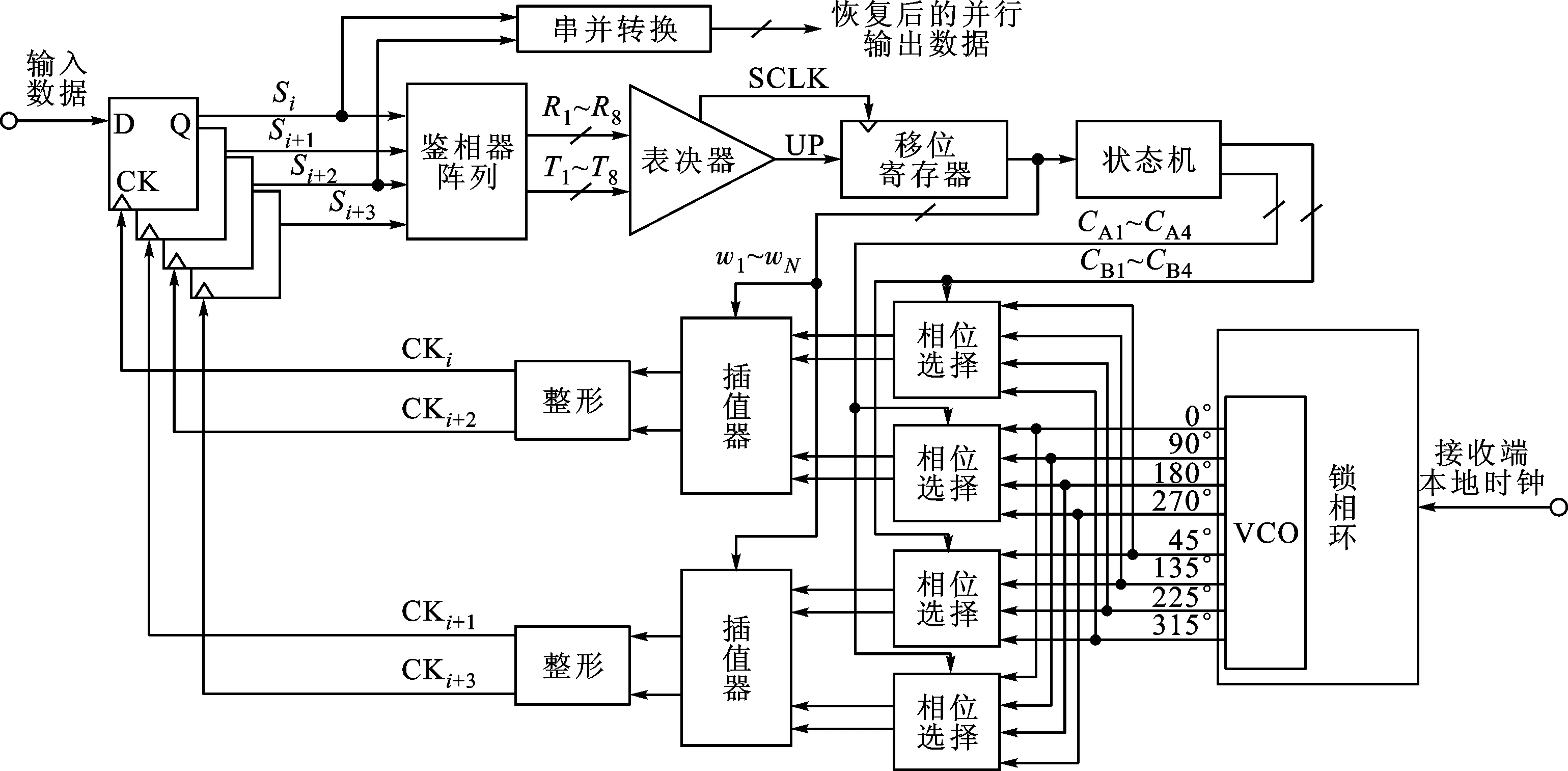
圖1 相位插值型CDR的整體結構

傳統插值器的尾電流源由多個等值電流源陣列組成,權重控制信號控制每個電流源的流通路徑,從而調整2個輸入信號差動對的尾電流的大小,使得輸出信號的相位在2個輸入信號相位之間插值。這種插值方法得到的輸出信號相位與權重控制信號的關系是非線性的,并且插值器的線性度與2個輸入信號的相位差有關,相位差越大,插值器的線性度越低[2]。文獻[3]中的仿真結果表明,對于90°的被插值信號相位差,傳統插值器的最大相位間隔偏離理想值37.6%,導致插值器相位調節的精度較低,恢復時鐘的抖動較大。國內外有很多關于降低相位插值器非線性的研究。文獻[4]通過產生按正弦規律變化的相位控制信號得到線性的相位輸出,但是這種方法只適用于輸入信號相位差為90°的情況而不能應用于45°的相位差。此外,電流源的非理想特性也降低了電流數模轉換器(DAC)的線性度。文獻[5]采用對2個子插值器的輸出進行平均的方法提升輸出相位的線性度,但2個子插值器增加了電路的面積和設計的復雜度。

本文在對傳統相位插值器進行建模分析的基礎上,提出了一種時鐘數據恢復電路中的線性相位插值器,能夠適用于多種相位差的插值,并且通過降低電流源開關驅動器的電壓,在不降低電壓擺幅的情況下實現了共源共柵尾電流源,可有效抑制溝道長度調制效應的影響。在所提出的線性插值器的基礎上,本文采用0.25 μm工藝,設計了一款應用于高速SERDES接口的CDR電路。仿真結果表明,所提出的線性相位插值器可有效降低CDR輸出時鐘的抖動。

1 相位插值型CDR的結構

1.1 系統結構

相位插值型CDR主要由采樣電路、鑒相表決器、移位寄存器、相位選擇電路、相位插值器等模塊組成。鎖相環中的VCO根據接收端的本地時鐘輸出8個相位間隔為45°的時鐘信號送到4個相位選擇電路。由2組控制信號CA1～CA4和CB1～CB4來控制相位選擇電路選擇出4組差動信號,分別送到2個插值器[6]。插值器在權重控制信號w1～w16的控制下,對輸入信號進行插值,微調輸出時鐘的相位。2個插值器輸出4個相位間隔為90°的信號,經過整形[7]后作為4個并行高速D觸發器[8]的輸入時鐘信號,對輸入串行數據進行采樣,并得到相應的采樣結果Si～Si+3。鑒相器陣列中的8個鑒相器對一定數量的連續采樣結果進行鑒相,產生2組指示時鐘超前或滯后信息的鑒相結果信號R1～R8和T1～T8。表決器對鑒相結果進行表決,并輸出UP信號來指示時鐘超前或滯后的判決結果。雙向移位寄存器在時鐘SCLK的控制下,根據UP信號的值移入1或0,改變w1～w16的值,調整采樣時鐘的相位。整個CDR電路系統構成一個負反饋結構,如圖1所示。系統鎖定時,采樣時鐘的上升沿對準輸入數據碼元的中間位置,實現最佳采樣[9]。

這種數字控制的相位調節是離散的。雙向移位寄存器根據表決器的表決結果移位,UP信號為1時,移位寄存器左移一個1,滯后則右移一個0,無跳變則不移位。當移位寄存器中的數據全為1或0時,狀態機切換狀態,相位選擇電路選擇相鄰區間進行插值,同時移位寄存器向相反方向移位。移位寄存器的輸出用來控制相位插值的權重,它的控制位數N決定了恢復時鐘的精度和CDR的頻率跟蹤范圍。理想情況下,每次調節的相位步進即恢復時鐘的精度是φ0/N,其中φ0為插值器輸入信號的相位差,φ0和移位寄存器的位寬N共同決定了相位插值的精度。圖2給出了φ0為45°、N=16時插值器的工作原理示意圖。工作過程中,CDR電路根據鑒相和表決結果不斷地調整采樣時鐘的相位,直到串行接收數據的相位剛好落在恢復時鐘的相鄰2個相位間隔內時,恢復時鐘的相位達到動態鎖定狀態。

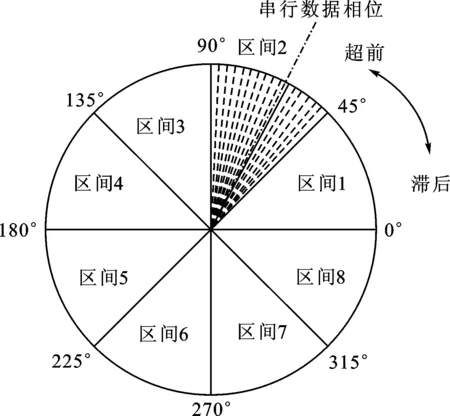
圖2 φ0為45°、N=16時相位插值器的工作原理

一般情況下,串行/解串(SERDES)接口的發送端和接收端的的時鐘并非同源時鐘,因此存在一定的頻率偏差。CDR的頻率跟蹤范圍指的是CDR能容忍的接收時鐘與發送時鐘的頻率偏差,若頻率偏差超出頻率跟蹤范圍,CDR就不能正確地恢復出接收時鐘。設發送時鐘的頻率為f,接收時鐘的頻率為f±Δf,則只要調整一次相位所需的時間即16個時鐘周期內積累的相位誤差小于一次相位調整的步進,這樣的頻率偏差就能容忍,即

(1)

從上面的分析中可以看出,N越大,相位步進越小,恢復時鐘的精度越高,但是CDR的頻率跟蹤范圍也會變小[9],因此移位寄存器的位數需要折中考慮。本文采用的移位寄存器位數為16位。

1.2 鑒相表決算法

鑒相器的作用是判斷時鐘相位超前還是滯后于數據跳變,但不能反映時鐘與數據的具體相位差。在時鐘存在抖動的情況下,單個鑒相器的鑒相結果是不準確的,因此需要多個鑒相器,并對它們的結果進行表決以增加鑒相結果的可靠性[10]。

CDR在接收的每16個串行數據位中,對其中9個連續數據位(Dn+1～Dn+9)進行鑒相和表決。為降低采樣時鐘的頻率并減小功耗,采樣電路采用相位差為90°的4相時鐘進行半速率采樣[3]。在1次鑒相過程中,共需要17個時鐘上升沿。第i(i=1,2,…,17)個時鐘上升沿CKi采樣得到的數據為Si。采用8個鑒相器對17個采樣結果進行鑒相,第k(k=1,2,…,8)個鑒相器對3個采樣結果S2k-1、S2k和S2k+1進行鑒相,得到鑒相結果Rk和Tk,從而判斷時鐘超前還是滯后于數據跳變,如圖3所示。

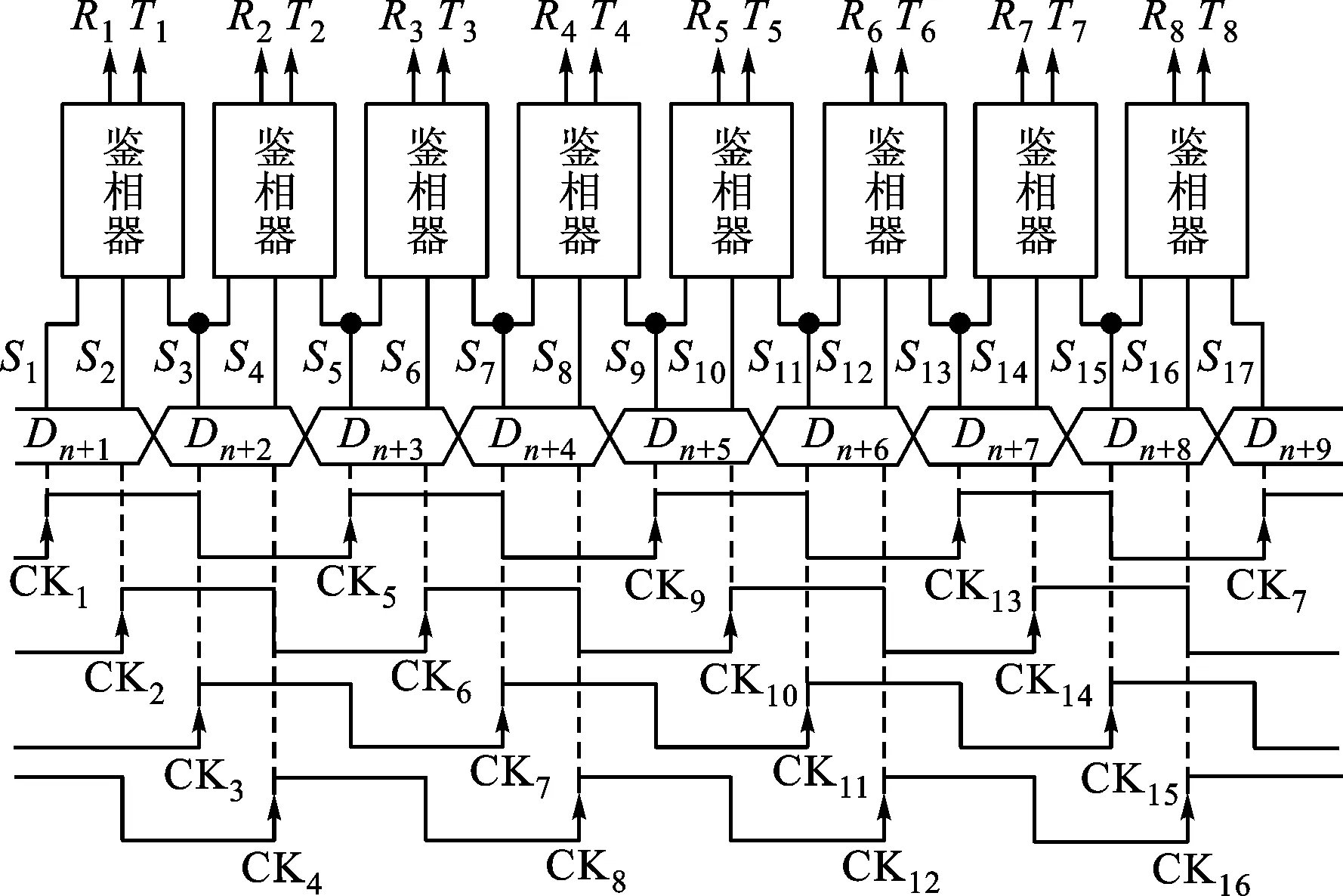
圖3 鑒相器工作原理示意圖

鑒相器的算法如下:

(1)若S2k-1?S2k=0,S2k?S2k+1=1,則時鐘上升沿超前數據跳變沿,Rk=1,Tk=0;

(2)若S2k-1?S2k=1,S2k?S2k+1=0,則時鐘上升沿滯后數據跳變沿,Rk=0,Tk=1;

(3)若S2k-1?S2k=0,S2k?S2k+1=0,則數據沒有跳變,Rk=0,Tk=0。

表決器對8個鑒相器的輸出進行統計,得到表決結果。具體表決算法如下:

(1)若∑Rk>∑Tk,則認為時鐘超前數據,并將UP信號置為1;

(2)若∑Rk<∑Tk,則認為時鐘滯后數據,將UP信號置為0;

(3)若∑Rk=∑Tk,則認為數據沒有跳變,移位時鐘SCLK在這個相位調整周期內不產生上升沿,移位寄存器不移位,插值電路保持不變。

1.3 相位插值電路

相位插值電路如圖4所示。相位插值器對2對具有一定相位差φ0的差動時鐘Vip1、Vin1和Vip2、Vin2進行相位插值,得到相位介于兩者之間的恢復時鐘[11];插值的權重控制信號w1～w16是移位寄存器中的16位數據,它通過改變2個差動對的尾電流來調整恢復時鐘的相位[5],尾電流控制著輸入管M1～M4的跨導。2對時鐘信號分別通過輸入管的跨導轉化為電流ID1～ID4。交叉求和得到的電流Iop和Ion的相位將介于2對時鐘之間,即實現了權重信號控制下的相位插值。

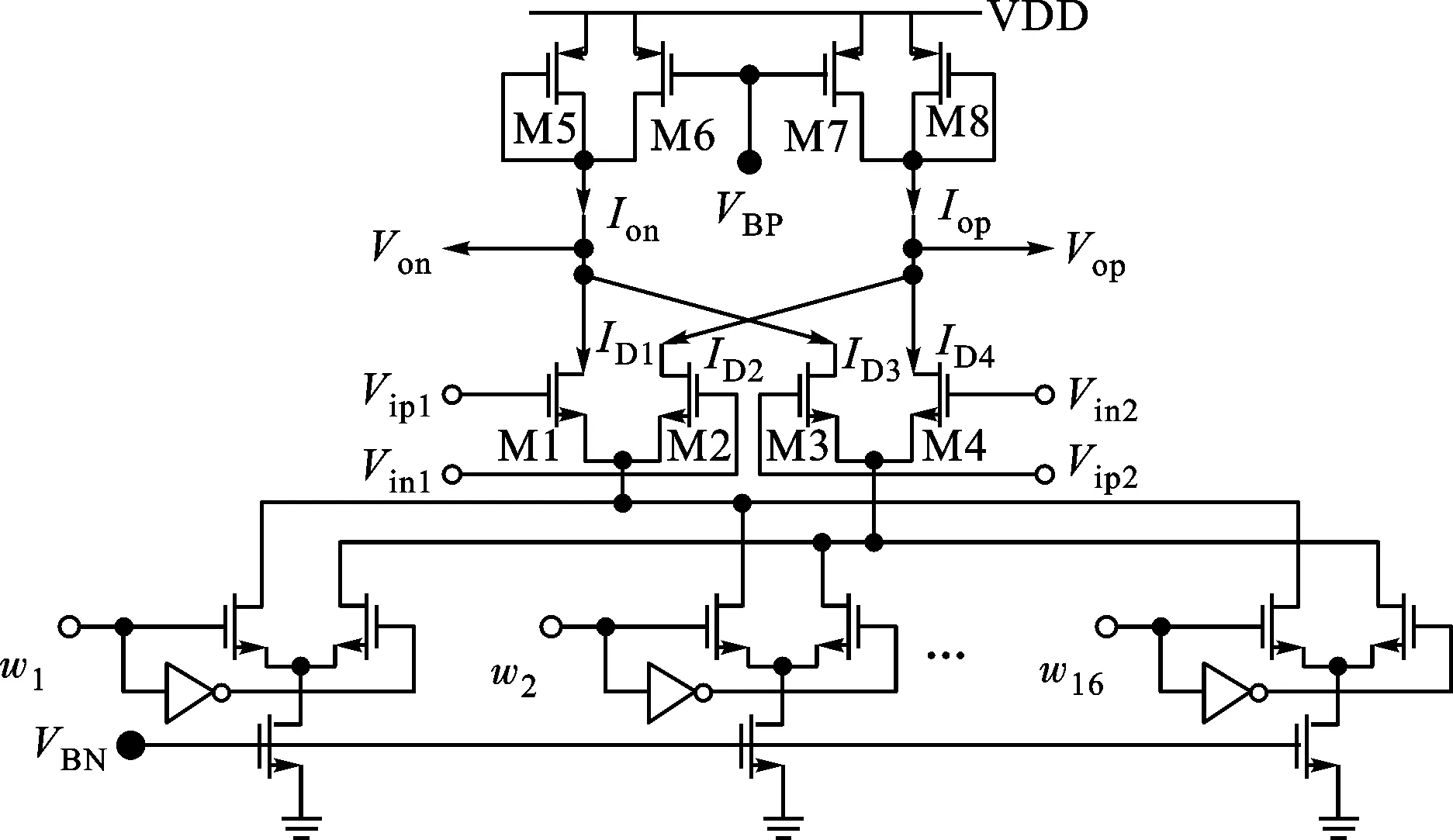
圖4 相位插值電路

2 傳統相位插值器的線性度分析

相位插值電路最重要的指標是它的線性度,即改變權重控制信號時,插值輸出時鐘相位是否線性變化。非線性的相位變化會導致插值輸出時鐘相位不均勻,輸出抖動也不均勻,恢復時鐘精度變低。

在圖4所示的相位插值電路中,假設所有尾電流源之和為I,且尾電流源晶體管尺寸相同,則在理想情況下,每個電流源的大小為(1/16)I。設權重控制信號w1～w16之和為w,那么差動對M1和M2的尾電流為(w/16)I,差動對M3和M4的尾電流為(1-w/16)I。令差動對M1和M2的權重a=w/16,則差動對M3和M4的權重為(1-a)。用半邊電路方法進行計算,則M1、M3的跨導為

(2)

(3)

式中:μn為電子遷移率;Cox為單位面積氧化層電容;(W/L)M1和(W/L)M3分別為M1和M3的寬長比。假定輸入差動信號Vip1、Vin1和Vip2、Vin2近似為正弦信號,振幅為V0/2,且它們的相位差為φ0,即

t)

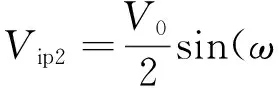
(4)

整個相位插值電路的負載采用對稱性結構,由鎖相環中的自偏置電路復制得到,從而保證2個PMOS管的電流大小相同,總體負載阻抗由M5決定[12],約為1/gM5。流過M5的電流ID5=Ion/2,其中,Ion=ID1+ID3=I/2,則ID5=I/4。那么M5的跨導可以表示為

(5)

式中:μp為空穴遷移率。由此,整個插值器半邊電路的輸出電壓可以表示為

(6)

將式(2)、(3)、(4)、(5)帶入式(6),得到輸出插值時鐘的表達式為

Von=k0sin(ωt+θ)(1+2(a(1-a))1/2cosφ0)1/2

(7)

(8)

(9)

式中:a為電流源權重。從前述可知,傳統相位插值器的尾電流源采用等值電流源陣列,w1～w16對插值器2個差動對尾電流的控制是線性的。然而,由式(9)可以看出,相位插值器輸出時鐘信號的相位與電流源權重a的關系顯然是非線性的。

另外,根據式(9),電流源權重a對輸出信號相位的控制關系還與插值器2個輸入信號的相位差φ0有關。為了更直觀地說明這種關系,圖5給出了φ0為不同值時,輸出信號相位與a之間的關系。可以看出,φ0越大,輸出相位的非線性越嚴重,因此要求減小φ0以降低非線性。然而,減小插值信號的相位差需要增加環形VCO的級數,從而會降低VCO的振蕩頻率,而且還會增加電路的功耗和面積。因此需要在輸出相位的線性度和電路的面積之間折中考慮。本文采用相位差為45°的2對互補時鐘進行插值。

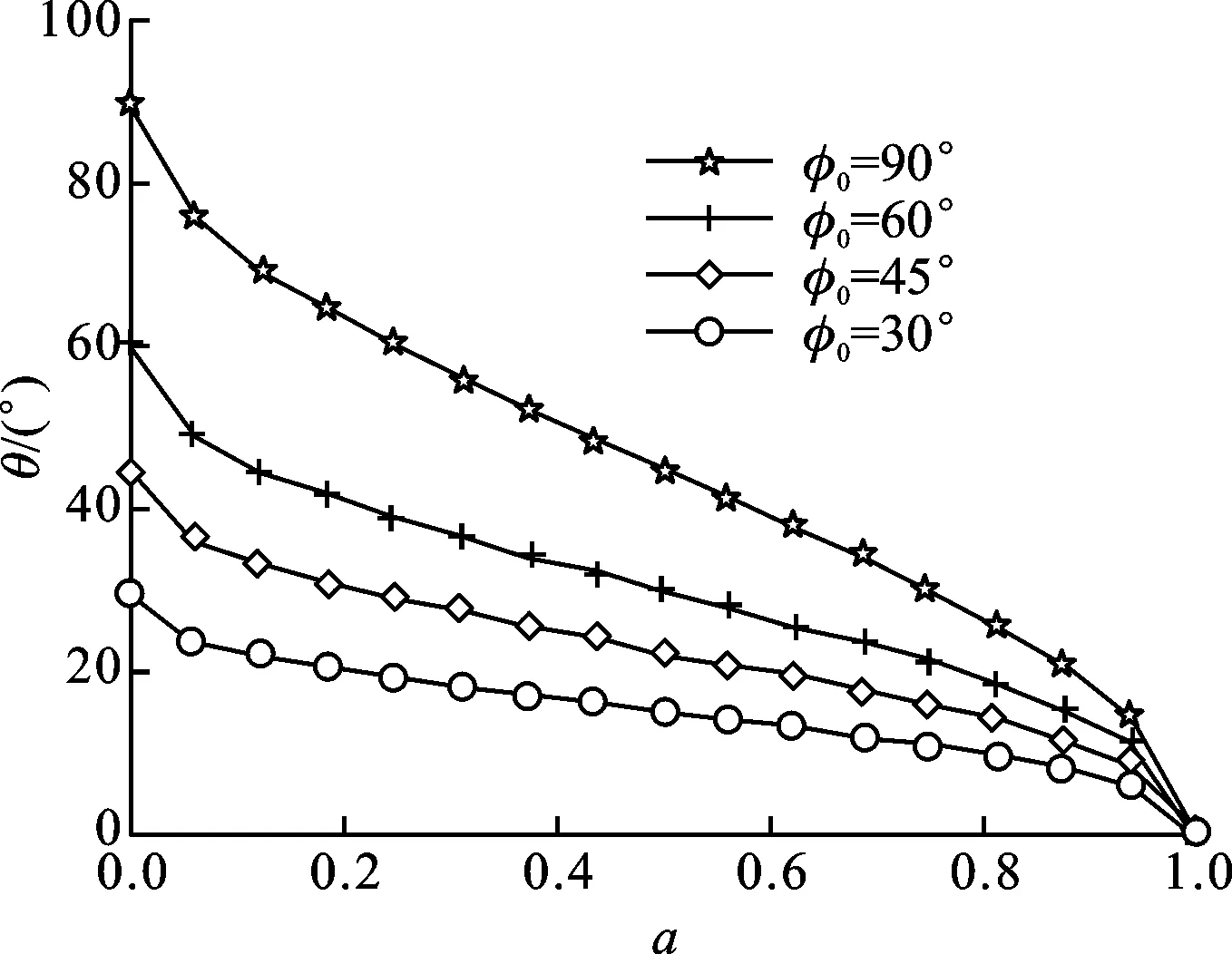
圖5 輸出插值信號相位與尾電流源權重的關系

在φ0為45°的情況下,若插值器的輸出相位具有理想的線性特性,則輸出信號的相位控制精度為45°/16=2.812 5°。在2.5 Gb/s的數據速率下,可以換算出CDR電路鎖定后輸出時鐘的確定性抖動的峰峰值為6.25 ps。實際上,由于相位插值器具有上述非線性特性,恢復時鐘相位的精度和確定性抖動的峰峰值由最大的相位步進決定。按照式(9)可以算出最大的確定性抖動的峰峰值為8.78 ps,因此為了降低抖動,對插值器進行相位線性化是非常必要的。

3 插值器的線性化方法

根據上面的分析,對插值器的輸出相位線性化就是要使權重控制信號之和w對輸出信號相位θ的控制是線性的,而w是通過改變插值器2個差動對尾電流源的權重a來實現相位調節的。若將w與a的函數關系表示為a=g(w),θ與a的函數關系表示為θ=f(a),則θ與w的函數關系為

θ=f[g(w)]

(10)

對于采用等值電流源陣列的傳統結構,a是w的線性函數(a=w/16),根據式(9)可以直接給出θ與a之間的非線性函數關系曲線,如圖6a所示。

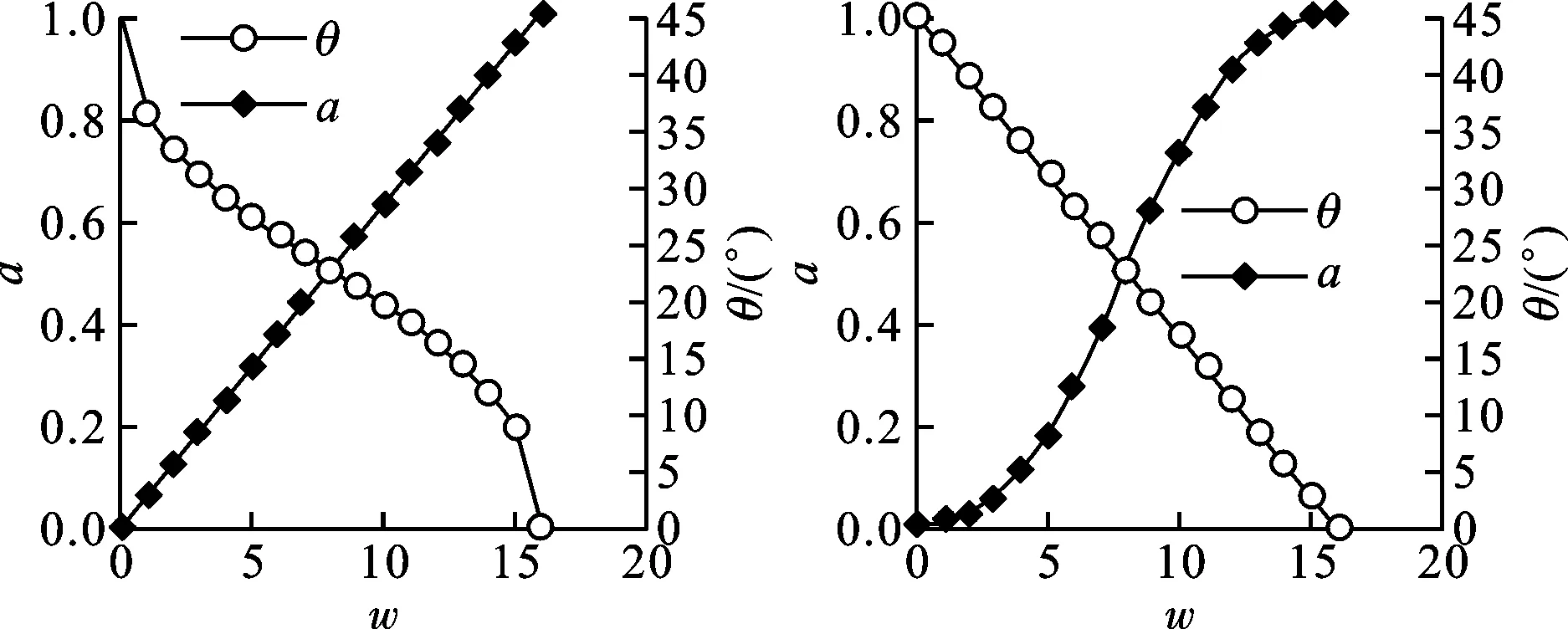
(a)非線性插值 (b)線性插值 圖6 控制權重w、尾電流權重a與輸出相位θ的變化關系

本文線性化方法的關鍵是按照圖6b的曲線,找出使θ=f(w)為線性函數的a=g(w),并在電路中實現。由于w、a和θ都是離散量,只要通過式(9)的反函數a=f-1(θ)計算出在0°～45°內均勻變化的17個θ值對應的a值,就可以反推出所需的非線性函數a=g(w)。實際實現時,保持總的尾電流源值不變,按照得出的a=g(w)確定出16個電流源的具體值,再確定出每只電流源晶體管的尺寸。可見,本文方法的優點是保持傳統電路結構不變,從而簡化電路設計。對于φ0為45°,N=16的情況,傳統結構每個電流源電流的大小占總電流的比例α為6.25%;按照本文提出的上述方法,可以得出16個電流源電流分別占總電流的比例關系如表1所示。

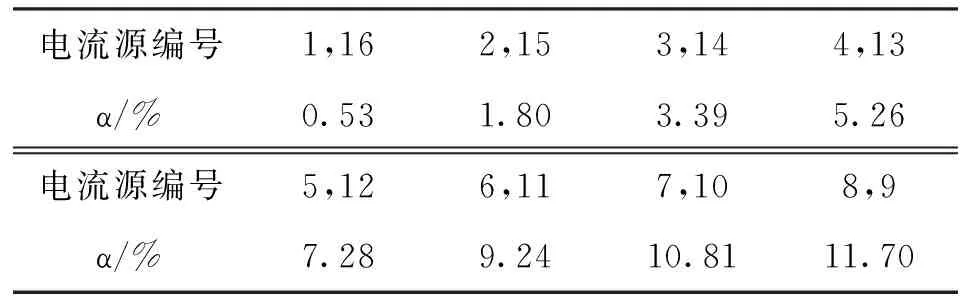
表1 本文提出的非等值電流源陣列的比例關系

按照上述方法,理論上可以實現完全線性的插值器。然而,上述的分析與計算沒有考慮電路的非理想效應。實際上,傳統插值器電路尾電流源陣列中的單個電流源由工作在飽和區的晶體管M1實現,控制信號C1通過開關管T1和T2來控制尾電流的流向,如圖7a所示。由于溝道長度調制效應的影響,陣列中各電流源之間的比例可能會出現較大的失配,從而嚴重降低插值器的線性度。

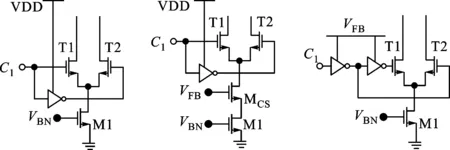
(a)單管電流源 (b)共源共柵電流源 (c)本文電流源圖7 3種電流源

降低溝道長度調制效應的一般方法是采用共源共柵結構,通過增加共柵管(MCS)和額外的偏置電壓VFB實現共源共柵結構,如圖7b所示。這種結構可以大大地降低溝道長度調制效應的影響,但是增加共柵管將會犧牲一定的輸出電壓擺幅,并增加了電路面積。

為了用共源共柵結構抑制溝道長度調制效應,并且不降低輸出電壓擺幅。本論文提出了一種改進的電流源結構,利用導通時的控制開關T1或T2作為共源共柵晶體管,并將驅動T1和T2的反相器的供電電壓降低為VFB,如圖7c所示。改進后,若某個開關管截止,則其柵壓為0,可以有效地關斷。開關導通時,柵壓為VFB,可以確保開關管工作在飽和區,實現共源共柵電流源,抑制了溝道長度調制效應,同時不影響電壓裕度。

4 仿真結果

本文采用TSMC 0.25 μm CMOS工藝設計了一款基于線性相位插值的CDR,電源電壓為2.5 V。

為了對比改進效果,圖8給出了采用等值電流源陣列的傳統相位插值器輸出信號的仿真結果,圖中每條曲線對應移位寄存器逐位變化時輸出結果。這些信號的相位調整步距由它們的過零點的時間間隔反映。仿真結果顯示,相位的變化規律與圖6所示的理論分析結果相同,接近相位調整區間邊界的相位步距較大,而區間中間的相位變化小,造成區間內相位分布很不均勻。最大的過零點時間間隔為10.23 ps,與理想特性的誤差為63.68%。

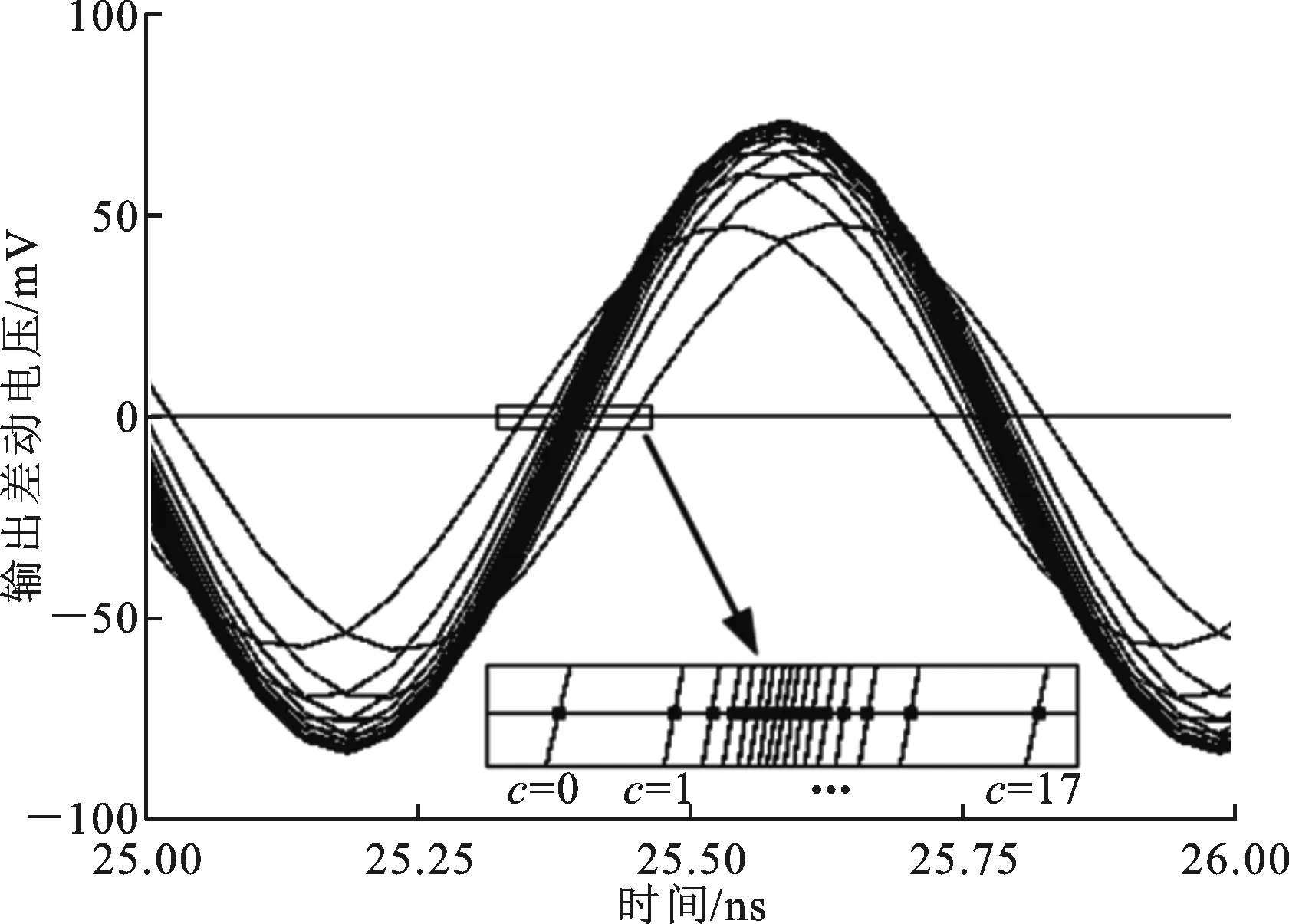
圖8 傳統相位插值器仿真結果

對于本文提出的采用非等值電流源陣列的插值器的仿真結果如圖9所示,可以看出,插值輸出時鐘的相位幾乎是等間隔的。圖中的最大時間間隔為6.84 ps,最小時間間隔為5.92 ps,最大誤差為(6.84-6.25)/6.25=9.44%。

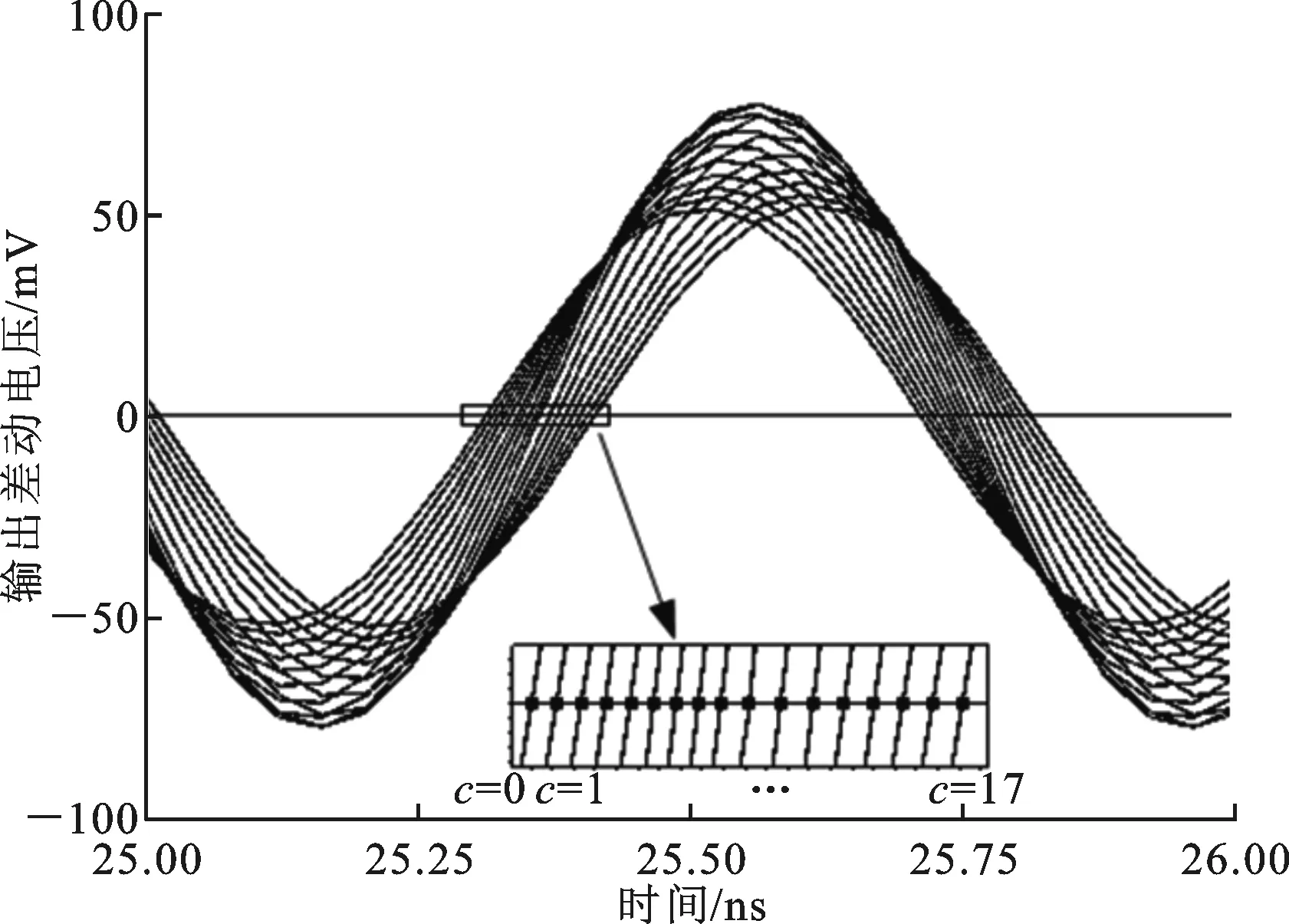
圖9 本文相位插值器仿真結果

考慮到版圖和工藝制造會影響器件的匹配度,對改進插值器進行蒙特卡羅仿真。尾電流管的寬、長、柵氧厚度和閾值電壓的失配度呈均值為0、標準差為1的高斯分布時,仿真結果如圖10所示,100次仿真的均值為6.5123 ps,標準差為0.7 ps。改進后的插值器能很好地抵抗器件不匹配的影響。

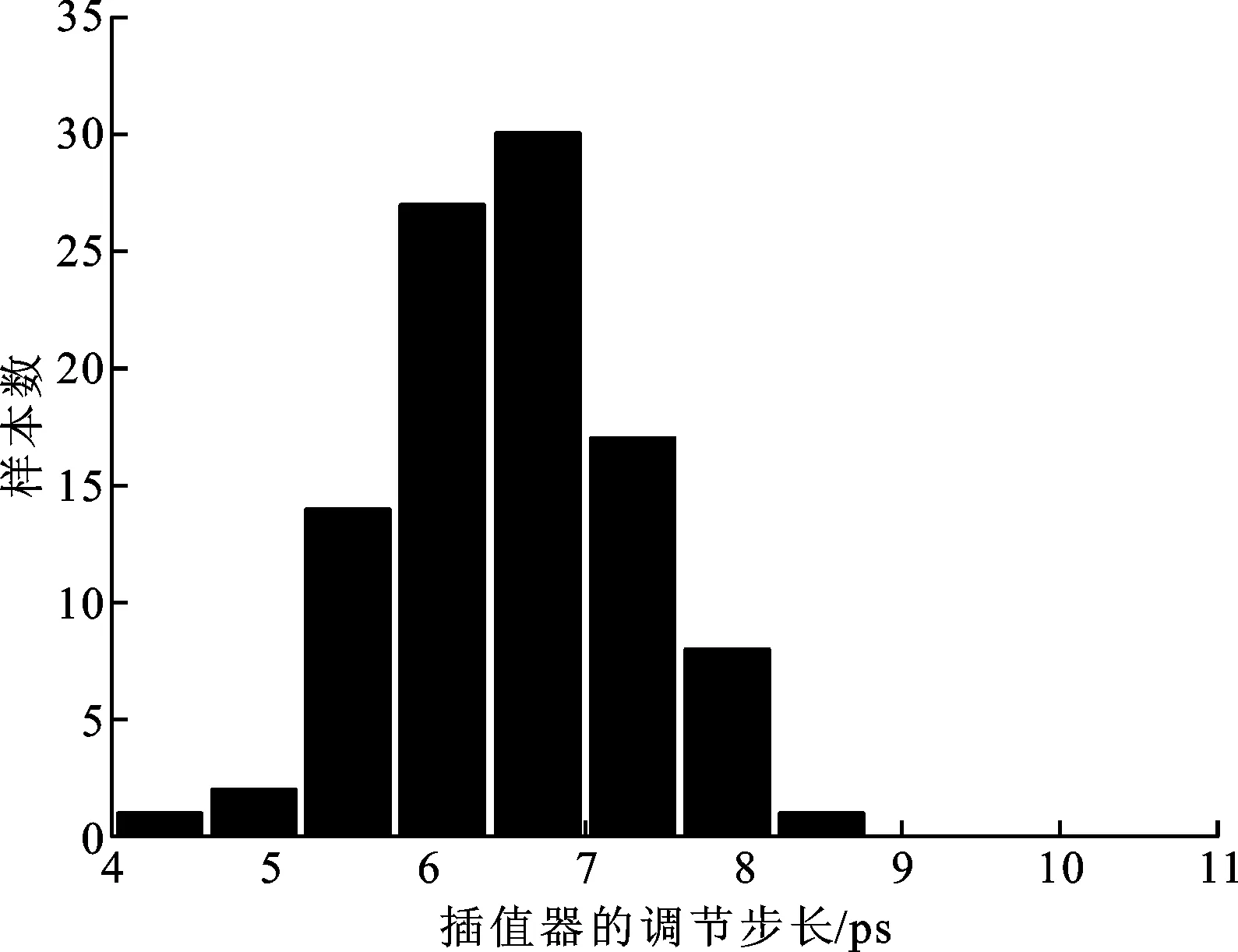
圖10 插值器調節步長的蒙特卡羅仿真結果

本文相位插值器的詳細參數在表2中進行了總結,并與一些相關文獻進行了對比,可見本文相位插值器通過改變權重的方法得到了很高的線性度。

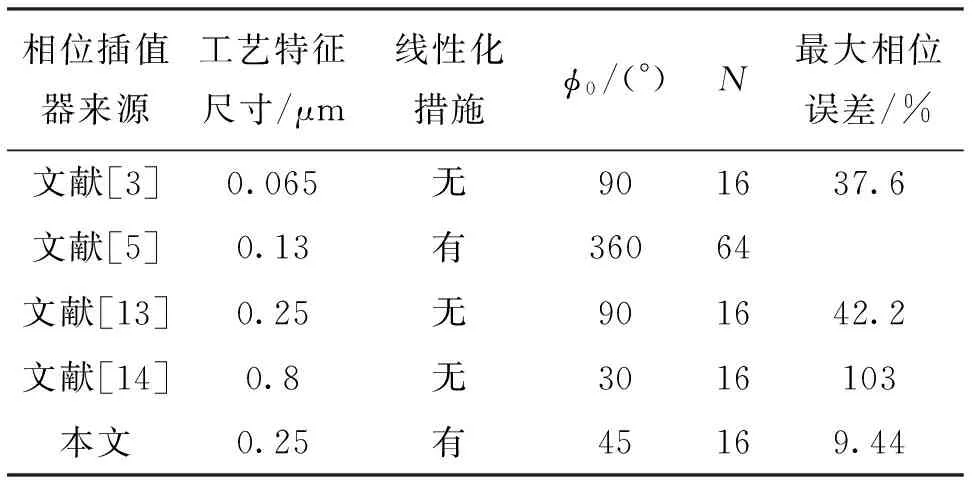
表2 插值器性能對比

在2.5 Gb/s的數據速率下,分別采用傳統的非線性插值器和本文提出的線性插值器對整個CDR的恢復時鐘的眼圖進行了仿真,仿真結果分別在圖11和圖12中給出。仿真中,CDR本地時鐘頻率與接收數據的時鐘頻率偏差設為0.02%。

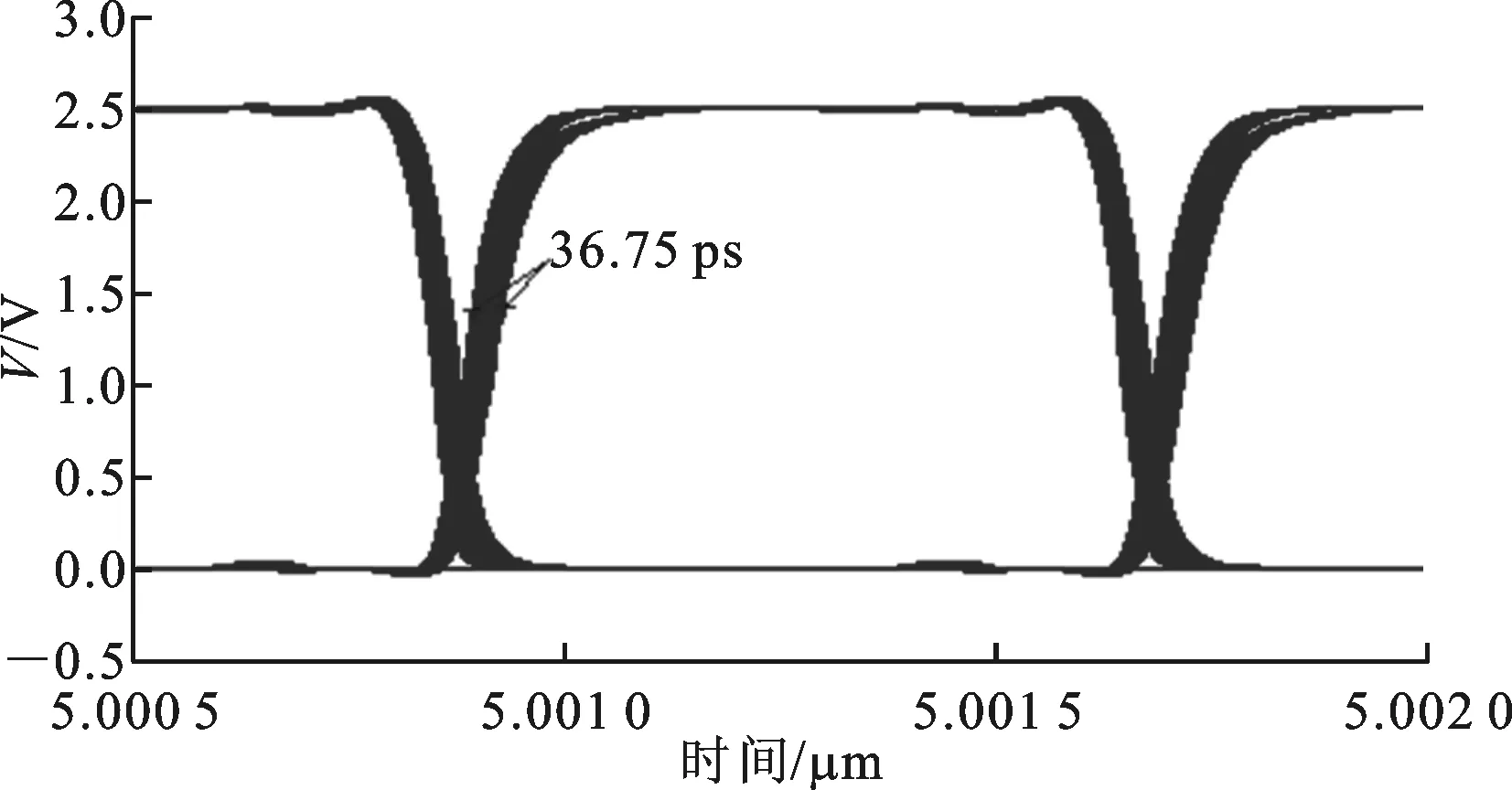
圖11 基于傳統插值器的CDR恢復時鐘的眼圖

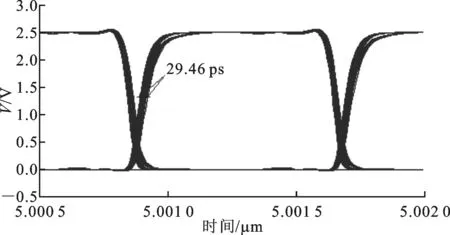
圖12 基于本文線性相位插值器的CDR恢復時鐘的眼圖

一般來說,在2.5 Gb/s的速率下,要達到10-12的誤碼率,時鐘抖動的峰峰值應小于49 ps[15]。對比圖11和圖12可見,采用本文提出的線性相位插值器將CDR輸出時鐘的抖動從36.72 ps降低為29.46 ps。整個CDR電路的功耗為106 mW。

5 總 結

本文提出了一種基于非等值電流源陣列的線性相位插值器。在對傳統相位插值器進行理論分析基礎上,按照電流權重與輸出相位的反函數關系,確定了電流源陣列中每個電流源的設計比例,有效地提高了輸出時鐘相位的線性度。本文采用0.25 μm CMOS工藝設計了一款基于線性相位插值器的CDR電路。仿真結果表明:傳統結構插值器的最大相位誤差為63.68%,而本文所提出的線性相位插值器的最大相位誤差僅為9.44%,可有效地降低CDR輸出時鐘的抖動。

[1] HSIEH M, SOBELMAN G E. Architectures for multi-gigabit wire-linked clock and data recovery [J]. IEEE Circuits and Systems Magazine, 2008, 8(4): 45-57.

[2] 孫燁輝, 江立新. 時鐘數據恢復電路中相位插值器的分析與設計 [J]. 半導體學報, 2008, 29(5): 930-935. SUN Yehui, JIANG Lixin. Analysis and design of a phase interpolator for clock and data recovery [J]. Journal of Semiconductors, 2008, 29(5): 930-935.

[3] HU Shijie, JIA Chen, HUANG Ke, et al. A 10 Gbps CDR based on phase interpolator for source synchronous receiver in 65nm CMOS [C]∥Proceedings of the 2012 IEEE International Symposium on Circuits and System. Piscataway, NJ, USA: IEEE, 2012: 309-312.

[4] CHEN L, SPAGNA F, MARZOLF P, et al. A 90 nm 1-4.25-Gbs multi data rate receiver for high speed serial links [C]∥Proceedings of IEEE Asian Solid-State Circuits Conference. Piscataway, NJ, USA: IEEE, 2006: 391-394.

[5] WEI Longfei, JI Jinyue, LIU Haiqi, et al. A multi-rate SerDes transceiver for IEEE 1394b applications [C]∥Proceedings of the 2012 IEEE Asia Pacific Conference on Circuits and Systems. Piscataway, NJ, USA: IEEE, 2012: 316-319.

[6] 李軒, 張長春, 李衛, 等. 2.5 Gb/s PS/PI型半速率時鐘數據恢復電路設計 [J]. 微電子學, 2014, 44(6): 793-797. LI Xuan, ZHANG Changchun, LI Wei, et al. Design of a 2.5 Gb/s PS/PI based half-rate clock and data recovery circuit [J]. Microelectronics, 2014, 44(6): 793-797.

[7] MANEATIS J G. Low-jitter process-independent DLL and PLL based on self-biased techniques [J]. IEEE Journal of Solid-State Circuits, 2002, 31(11): 1723-1732.

[8] STROLLO A G M, DE CARO D, NAPOLI E, et al. A novel high-speed sense-amplifier-based flip-flop [J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2005, 13(11): 1266-1274.

[9] SOH L K, WONG W T, LEE S W, et al. Programmable low-dithering-jitter interpolator-based CDR [C]∥Proceedings of 13th International Symposium on Integrated Circuits. Piscataway, NJ, USA: IEEE, 2011: 444-447.

[10]HE M Y, POULTON J. A CMOS mixed-signal clock and data recovery circuit for OIF CEI-6G+backplane transceiver [J]. IEEE Journal of Solid-State Circuits, 2006, 41(3): 597-606.

[11]KREIENKAMP R, LANGMANN U, ZIMMERMANN C, et al. A 10-Gb/s CMOS clock and data recovery circuit with an analog phase interpolator [J]. IEEE Journal of Solid-State Circuits, 2005, 40(3): 736-743.

[12]MANEATIS J G, HOROWITZ M A. Precise delay generation using coupled oscillators [J]. IEEE Journal of Solid-State Circuits, 1993, 28(12): 1273-1282.

[13]FUKAISHI M, NAKAMURA K, HEIUCHI H. A 20-Gb/s CMOS multichannel transmitter and receiver chip set for ultra-high-resolution digital displays [J]. IEEE Journal of Solid-State Circuits, 2000, 35(11): 1611-1618.

[14]SIDIROPOULOS S, HOROWITZ M A. A semidigital dual delay-locked loop [J]. IEEE Journal of Solid-State Circuits, 1997, 32(11): 1683-1692.

(編輯 劉楊)

A Linear Phase Interpolator for Clock and Data Recovery Circuits

ZHANG Yao1,ZHANG Hong1,LI Liang2,DU Xin1,CHENG Jun1

(1. School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. Key Laboratory of Analog Integrated Circuit, No.24 Research Institute China Electronic Technology Group Corporation, Chongqing 400060, China)

A linear phase interpolator based on non-equal current source array is presented to solve the problem of increasing clock jitter caused by the non-linearity of phase interpolator in clock and data recovery circuit. According to the inverse function relationship between the phase of the output clock and the weights of the tail current sources, the ratio of each current source in the tail current source array of the interpolator is adjusted elaborately based on the traditional phase interpolator. Moreover, the control transistor is used as a common gate transistor so as to improve the matching degree and the stability of the current source. Thus the linear relation between the phase of the output clock and the control signals is realized. The regulation precision of CDR is improved while the jitter in recovering clock is reduced. A clock and data recovery circuit based on the presented linear phase interpolator is designed using the 0.25 μm CMOS technology. Simulation results show that the maximum phase error of the proposed linear phase interpolator is 9.44%, while the maximum phase error of the traditional interpolator is 63.68%, that is, the presented interpolator significantly reduces the clock jitter of the CDR.

clock recovery; phase interpolation; linearity; jitter

2015-08-17。

張瑤(1991—),女,碩士生;張鴻(通信作者),男,副教授。 基金項目:國家自然科學基金資助項目(61474092);陜西省科技計劃資助項目(2014K05-14);模擬集成電路重點實驗室基金資助項目(140C09044)。

時間:2015-12-02

10.7652/xjtuxb201602009

TN432

A

0253-987X(2016)02-0048-07

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151202.1857.002.html