復雜電磁邊界下基于曲線坐標的保角變換法

張婧思,苗英愷,劉曉波,張安學

(1.西安交通大學電子與信息工程學院, 710049, 西安;2.濮陽職業技術學院, 457000, 河南濮陽)

?

復雜電磁邊界下基于曲線坐標的保角變換法

張婧思1,苗英愷2,劉曉波1,張安學1

(1.西安交通大學電子與信息工程學院, 710049, 西安;2.濮陽職業技術學院, 457000, 河南濮陽)

針對具有復雜幾何邊界條件的二維均勻微波傳輸線中電磁場難以解析求解從而造成其設計困難的問題,提出了一種基于曲線坐標的保角變換法(CMM)。該方法基于二維傳輸線的橫電磁場(TEM)模型。首先利用保角變換將復雜傳輸線的邊界曲線映射為簡單傳輸線的邊界曲線,建立復雜邊界傳輸線的曲線坐標;然后利用曲線坐標把復雜邊界傳輸線所滿足的麥克斯韋方程轉換到簡單邊界傳輸線中,形成兩種傳輸線間的電磁映射;最后論證了兩種傳輸線間電荷、電位分別對應相等,由此得到了與傳輸特性緊密相關的復雜傳輸線的電容,進而用以指導傳輸線的設計。由于以電位為中間量的傳統保角變換計算較為復雜,采用CMM方法直接從場出發,省去了關于電位的中間計算過程,簡化了計算過程。仿真結果表明,不同尺寸下同軸線特征阻抗仿真值與理論值吻合得很好,驗證了CMM方法的正確性。

微波傳輸線;曲線坐標;保角變換;麥克斯韋方程

在微波工程中,二維均勻微波傳輸線是許多微波電路實現的基礎。然而,對于各種邊界復雜、性能迥異的非常規傳輸線,直接求解其電磁場的麥克斯韋方程卻幾乎難以實現。因此,精確分析與綜合設計這些微波傳輸線已成了相關人員面臨的迫切問題。

目前對于此問題的研究主要分為數值法和解析法。數值法是伴隨著近些年計算機技術的發展而活躍起來的,主要有時域有限差分法(FDTD)[1]、矩量法[2]等。FDTD基于麥克斯韋方程的時域差分形式,其優點是適合于寬帶計算,計算時間短,但缺點是難以計算電大尺寸物體,對計算機性能要求比較高;矩量法基于電磁場的變分原理,通過選擇一組基函數去近似真實的場分布,優點是過程簡單,求解步驟統一,應用起來比較方便,但缺點是需要一定的數學技巧,如基函數與權函數的選取,同時為了達到所需要的計算精度,矩量法的計算任務也很繁重。解析法則主要有直接法、變分法[3]等。直接法即是求解電磁場所滿足的麥克斯韋方程,但這種方法由于邊界過于復雜,一般很少采用;變分法是建立某些參量的穩定泛函,從而獲得該參量的解析閉式,其結果對于器件的綜合設計可以提供較好的指導作用,缺點是閉式的精度難以保證,與試探函數的選取有重要關系。此外,部分學者[4]嘗試利用近些年發展起來的變換光學[5]解決此類問題,通過坐標變換將復雜邊界變換為規則邊界,而其他方法則一般需要在變換區域填充復雜介質,最后再利用數值方法進行求解,因此可以算是一種半解析半數值的方法,雖由此降低了計算的難度,但缺點是仍不能獲得解析閉式。因此,問題的關鍵在既能較精確地分析器件場分布,又能獲得一些參量較精確的解析閉式,用以指導器件的綜合設計。

針對以上問題,本文提出了一種基于曲線坐標的保角變換(CMM)方法。首先,對于復雜傳輸線的的幾何邊界,總可以通過直線逼近,建立適當的保角變換,將其變換為簡單傳輸線的幾何邊界;其次,保角變換法可以得到精確的解析結果,這對于器件的綜合設計具有重要意義;此外,對于傳統方法較難解決的性能迥異的非常規傳輸線問題,采用CMM方法可以直接從場出發,省去關于電位的中間計算過程,在保證計算精度的同時,可有效節約計算資源。

1 理論模型

對于微波工程中具有復雜幾何邊界條件的二維傳輸線,分析傳輸線的場分布是傳輸線綜合設計的第一步,之后再利用分析結果指導傳輸線的設計。

首先,利用保角變換法求解復雜幾何邊界條件的二維傳輸線,以最簡單的圓同軸為例進行討論。同軸線截面和平行板截面模型如圖1所示,已知真空中圓同軸內外半徑分別為a、b。該同軸線幾何邊界作保角變換映射為一有限長度平行線(平行板),映射關系如下

(1)

式中:(x,y)為同軸線系統的直角坐標;(u,v)為同軸線系統的曲線坐標,同時也是平行板系統中的直角坐標。

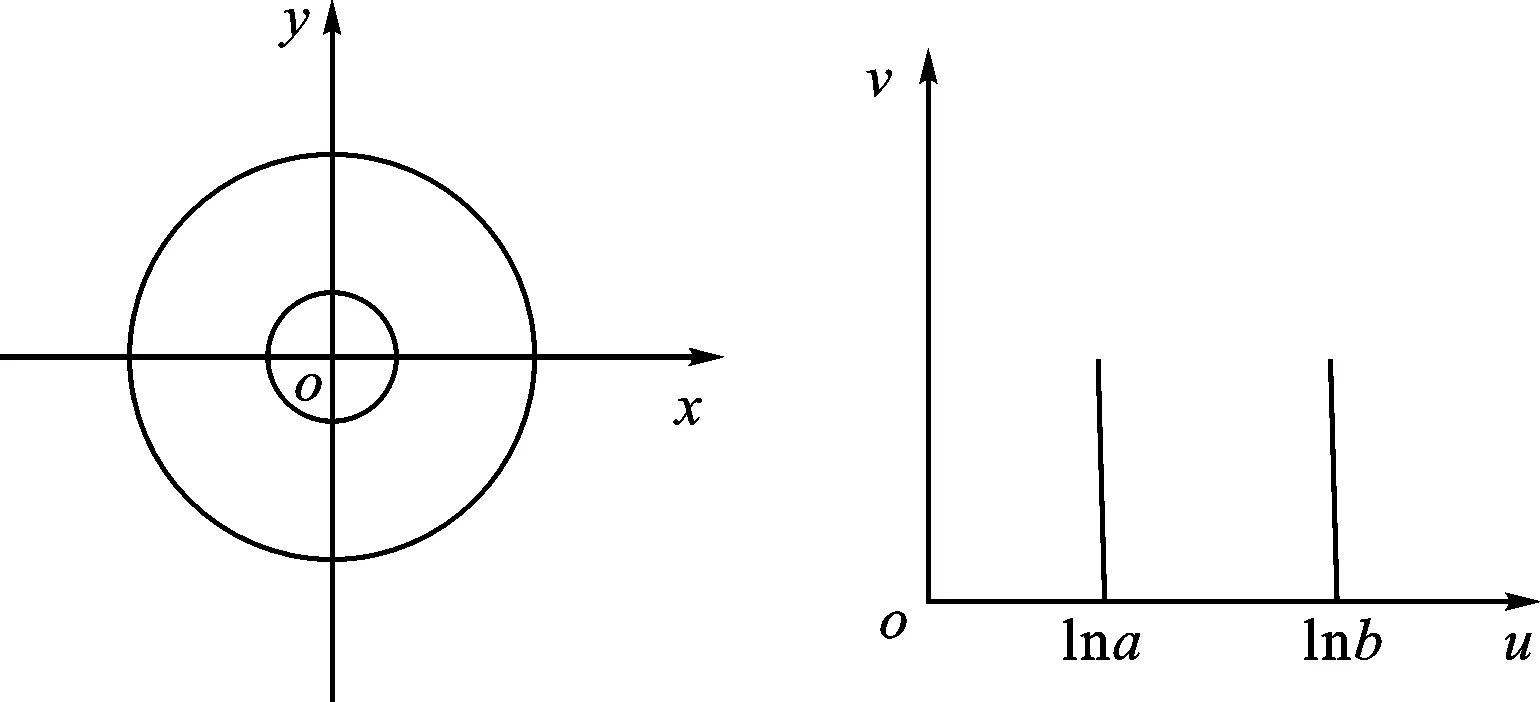
(a)同軸線截面 (b)平行板截面圖1 同軸線截面和平行板截面

為了分析同軸線中的場分布,首先假設同軸線中的場在直角坐標系(x,y)中為如下形式

(2)

公式滿足真空中的麥克斯韋方程,式中Ex、Ey、Bx、By為同軸線中的電場和磁場在直角坐標系(x,y)下的直角分量。

其次,為了建立同軸線與平行板中的場分布的映射關系,將上述同軸線中的場分布式(2)改寫在曲線坐標系(u,v)中,此時有下式成立

(3)

式中:Eu、Ev、Bu、Bv是同軸線中的場分布在曲線坐標系下的逆變分量,與直角分量存在如下關系

(4)

最后,將同軸線中的場分布代入真空中的麥克斯韋方程,并將其表示在曲線坐標系(u,v)中,具體形式如下

(5)

式中:ρ1是電荷密度;j1是電流密度;g1/2是保角變換度規矩陣的行列式;Eu、Ev、Bu、Bv是同軸線中的場分布在曲線坐標系下的協變分量,其中,Eu和場的逆變分量Eu存在關系Eu=g1/2Eu

通過上述分析可以發現,式(5)恰為平行板中直角坐標(u,v)的場分布所滿足的二維麥克斯韋方程組。因此,可以得出平行板中的場源如下

(6)

至此,在保角變換的約束下,利用曲線坐標從麥克斯韋方程出發,建立了變換前后兩種傳輸線間的電磁映射關系,即同軸線中的場源總是可以用平行板中的場源進行表示。

2 電容的計算

對于二維均勻微波傳輸線而言,可以通過場的方法(場模型)進行求解分析。由于二維均勻微波傳輸線一般涉及橫電磁場(TEM),因此可以建立更為簡單有效的電路模型,其中電路參數由場分布決定。對于傳輸線的電路模型而言,與其傳輸特性緊密相關的常數如衰減常數[6]和特征阻抗[7-11]都可以利用電容求得,而電容是與傳輸線的尺寸相關。因此,電容對于傳輸線的指導設計具有重要意義。

考慮到電容定義C=Q/V,其中Q為單位長度傳輸線的電荷,V為傳輸線兩導體間的電壓,因此可以利用CMM方法建立單位長度同軸線與平行板間電荷、電位的數學關系,從而得出兩傳輸線間的電容關系。

2.1 電荷的變換關系

為了求解兩傳輸線間的電荷關系,首先考慮變換前后兩傳輸線對應的微小體積元中電荷的關系,對于兩者間對應的任意微小體積元存在數學關系dxdy=g1/2du1du2,再利用變換前后兩傳輸線電荷密度的關系式(6)求解。可以論證:保角變換導致了傳輸線體積的變化和電荷密度的反比例變化,從而保證了電荷的變換相等。變換關系式如下

(7)

式中:dQ1是同軸線系統單位積元中的電荷;dQ2是平行板系統單位體積元中的電荷。

除此之外,還可以驗證同軸系統中的電流連續性方程映射為平行板系統中的連續性方程,從側面說明了映射后平行板系統中的電荷與電流之間是自洽的,沒有違背基本的電荷守恒定律。在同軸線中,電流連續性方程如下

(8)

如果將式(8)用同軸系統中的曲線坐標系(u,v)表示,則有

(9)

顯然,式(9)恰為平行板系統中的電流連續性方程。至此得到了保角變換前后,單位長度同軸與平行板電荷之間變換相等,同時也驗證了映射后的平行板系統具有自洽性。

2.2 電位的變換關系

對于二維均勻傳輸線,由于其一般涉及TEM場,而此電場是梯度場,因此可以定義任意兩點間的電壓如下

V=∫E·dr

(10)

利用式(10),可以計算同軸線中任意兩點間的電位差V1與平行板中對應兩點間的電位差V2之間的關系。V1與V2的表達式如下

V1=∫Exdx+∫Eydy

(11)

V2=∫Eudu+∫Evdv

(12)

為論證V2與V1的關系,可以把V2表達式中的參量Eu、u等用同軸系統中的直角參量Ex、x等表示,并考慮到保角變換的柯西-黎曼條件,可將上式化簡如下

(13)

最后,只需要利用下述雅可比行列式關系,就可化簡式(13),建立起V2與V1的關系

(14)

計算可得

(15)

將式(15)代入式(13)可得

V2=∫Exdx+∫Eydy

(16)

至此,從上式可以得出結論:同軸系統中任意兩點與平行板系統中對應兩點的電位差保持不變。

從電容的基本定義出發,根據兩傳輸線間的電荷和電位的變換關系可以得出:單位長度的同軸與平行板電容相等,即保角變換具有保電容性。這與之前的研究結論[12]是一致的。

對于工程實際所需要的傳輸線,可以從傳輸線參量如特征阻抗、衰減常數出發,求得傳輸線的電容,最后再利用電容,求得傳輸線相應的尺寸。

2.3 算例驗證

為了驗證本文CMM方法的有效性,具體計算同軸線場分布及電容值。

首先,利用式(4)建立同軸系統場的直角分量與其在(u,v)曲線坐標下的協變分量Eu、Ev之間的關系如下

(17)

其次,由于同軸線關于角度是周期的,因此在(u,v)直角平面可無限延伸,故而在平行板系統中,Eu、Ev作為平行板場的直角分量滿足下式

(18)

然后,在已知平行板電場分布Eu、Ev的前提下,將式(18)代入式(17),即可得出同軸線場的直角分量Ex、Ey

(19)

(20)

則電場矢量可表示為

(21)

至此,即通過曲線坐標法,利用平行板的場分布反演出了同軸線的場分布。從上述過程可清晰看到,在平行板逐漸彎曲為同軸線過程中,平行板中的電場也在逐漸的擴散,以適應邊界。可以驗證,式(21)與參考文獻[13]中的相應公式是一致的。

最后,利用已求得的場分布,計算同軸導體內外的電壓和電荷。單位長度同軸線與平行板上電荷為

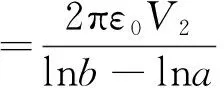
(22)

(23)

同樣,利用電壓定義,可求得同軸內外導體間的電壓如下

(24)

式(22)～式(24)與第2節中關于電荷電壓的結論一致,從而驗證了本文方法的正確性。利用電容定義即可求得單位長度同軸線的電容

(25)

考慮到工程實際需求,由電容即可求得同軸線的關鍵參量特征阻抗

(26)

利用CMM方法計算了同軸線的場分布及電容等參量,結論與之前的理論分析一致。對于工程實際所需要的傳輸線,可以從其傳輸線參量如特征阻抗出發,求得傳輸線的電容,再利用電容求得傳輸線相應的尺寸,完成設計過程。

2.4 仿真驗證

利用商業軟件CST2013可仿真得出不同尺寸下同軸線的特征阻抗。設置工作頻率為3 GHz,內半徑a=1 mm,導體具有理想電邊界,內外導體中間填充空氣。表1給出了在上述仿真條件下,不同外半徑時同軸特征阻抗的仿真結果與理論結果。

從表1中可以看出,在不同尺寸下,同軸特征阻抗理論值與數值仿真結果吻合得很好,從而說明了本文CMM方法的正確性。

表1 不同外半徑下同軸特征阻抗

3 結 論

本文針對復雜邊界條件下的二維均勻傳輸線中電磁場難以解析求解從而造成設計困難的問題,提出了一種基于曲線坐標的保角變換法——CMM方法,并以同軸線為例,展示了這種方法的計算過程。首先通過保角變換,建立同軸線與平行板間的數學聯系;然后,利用曲線坐標建立了場源在同軸線和平行板間的映射關系,得出了同軸線的場源分布;最后,利用同軸線中的場分布建立了同軸線等效電路模型,模型中與電路傳輸特性相關的參量與電容緊密相關,且電容與傳輸線的尺寸相關,這樣就形成了一個完整的分析與設計過程。本文方法相比于以電位為中間量的傳統保角變換,直接從場出發,省去了關于電位的中間計算過程,在保證計算精度的同時,有效節約了計算資源。仿真結果表明,不同尺寸下同軸線特征阻抗仿真值與理論值吻合得很好,說明了CMM方法的正確性。本文方法并不局限于真空環境,也適用于各向同性介質,且有望推廣到三維微波器件。

[1] DEY S, MITTRAA R. Locally conformal finite-difference time-domain (FDTD) algorithm for modeling three-dimensional perfectly conducting objects [J]. IEEE Microwave and Guided Wave Letters, 1997, 9(7): 273-275.

[2] HAMILTON L R, STALZER M A, TURLEY R S. Method of moments scattering computations using high-order basis functions [EB/OL]. [2015-03-05]. http:/ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=385149.

[3] 崔翔, 謝羲. 計算電容值的變分與互補變分法 [J]. 華北電力學院學報, 1990, 17(2): 1-6. CUI Xiang, XIE Xi. Variational and complementary variational method for calculating capacitance [J]. Journal of North China Institute of Electric Power, 1990, 17(2): 1-6.

[4] 倪中非, 黃斌科, 師振盛. 用于非規則波導傳輸特性分析的高效坐標變換法 [J]. 西安交通大學學報, 2014, 48(8): 18-22. NI Zhongfei, HUANG Binke, SHI Zhensheng. An efficient coordinate transformation method for propagation properties analysis of irregular waveguide [J]. Xi’an Jiaotong University, 2014, 48(8): 18-22.

[5] PENDRY J B, SCHURIG D, SMITH D R. Controlling electromagnetic fields [J]. Science, 2006, 312: 1780-1782.

[6] 梁昌洪, 崔鐵軍, 范小平. 采用保角變換求解一類TEM模傳輸線的衰減常數 [J]. 電子科學學刊, 1991, 13(5): 475-481. LIANG Changhong, CUI Tiejun, FAN Xiaoping. Conformal transformation method for attenuation constant of TEM mode transmission line [J]. Journal of Electronics, 1991, 13(5): 475-481.

[7] DUYAR M, AKAN V, YAZGAN E, et al. Analytical attenuation calculation of asymmetrical coplanar waveguide with finite-extent ground planes for coplanar, waveguide mode [J]. Microwave and Optical Technology Letters, 2007, 49(6): 2082-2087.

[8] ZHAO Ji-Xiang. Characteristic parameters for CPWS on a very thin dielectric layer [J]. Microwave and Optical Technology Letters, 2005, 45(3): 240-241.

[9] AKAN V, YAZGAN E. Quasistatic TEM characteristics of multilayer elliptical and cylindrical coplanar waveguides [J]. Microwave and Optical Technology Letters, 2004, 42(4): 317-322.

[10]SHAN Zhiyong, ZHANG Yanhua, ZHOU Xilang, et al. Analytical analysis of a rectangular shielded multilayer coupled coplanar waveguide [J]. Microwave and Optical Technology Letters, 2004, 41(5): 392-395.

[11]AKAN V, YAZGAN E. A simple formulation for quasistatic solutions of elliptical, cylindrical and asymmetrical coplanar strip lines [J]. Microwave and Optical Technology Letters, 2004, 41(1): 18-21.

[12]王福謙. 橢圓柱傳輸線內的TEM波及其特性阻抗 [J]. 光纖與電纜及其應用技術, 2011(5): 1-3, 11. WANG Fuqian. TEM wave and characteristic impedance of the elliptical cylinder transmission line [J]. Optical Fiber & Electric Cable, 2011(5): 1-3, 11.

[13]李宗謙, 佘京兆, 高葆薪. 微波工程基礎 [M]. 北京: 清華大學出版社, 2004: 113-114.

(編輯 劉楊)

A Conformal Mapping Method Based on Curve Coordinates under Complex Electromagnetic Boundaries

ZHANG Jingsi1,MIAO Yingkai2,LIU Xiaobo1,ZHANG Anxue1

(1. School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. Puyang Vocational and Technical College, Puyang, Henan 457000, China)

A conformal mapping method (CMM) based on curve coordinates is proposed to focus on the problem that the electromagnetic field of the two-dimensional uniform microwave transmission lines with complex geometric boundary conditions is hard to be analytically solved and thus its design is difficult. The method is based on a TEM model of the cross-dimensional electromagnetic transmission line. First, the conformal mapping is used to map the complex boundary curve of the transmission line into boundary curves of a simple transmission line, and the curvilinear coordinates of the complex border transmission lines are built; Then the curvilinear coordinates are used to convert the Maxwell’s equations for the complex border transmission lines to the simple border transmission lines, and the electromagnetic mapping between the two kinds of transmission line is formed. Finally, it is verified that both the charge and the potential between two kinds of transmission lines are correspondingly equal, so that the capacitance of complex transmission line that is closely related to the transfer characteristic is obtained and can further be used to guide the design of the transmission line. Simulation results and comparisons with the traditional conformal mapping calculation method with the potential being the intermediate amount show that the CMM method starts directly from the field, eliminates the potential on the intermediate calculations, and its results agree well with theoretical calculation.

microwave transmission lines; curve coordinates; conformal mapping; Maxwell’s equations

2015-04-30。

張婧思(1992—),女,碩士生;張安學(通信作者),男,教授,博士生導師。 基金項目:國家自然科學基金資助項目(61471292,61331005,61471388,41404095)

時間:2015-11-27

10.7652/xjtuxb201602008

TN81

A

0253-987X(2016)02-0043-05

網絡出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151127.2116.006.html