解決電場中運動問題的四種基本思想

安徽省壽縣一中 楊德明

解決電場中運動問題的四種基本思想

安徽省壽縣一中 楊德明

帶電粒子在電場中的運動問題是電場中的重要問題之一，也是高考的熱點。本章中的物理公式、概念和規律很多，用到的物理思想方法也多。為了理順關系，清除學習上的障礙和思維盲點，筆者認為，對于解決這類問題，我們應掌握并靈活運用四種常見的解決問題的思想，即力和運動的思想、分解的思想、功能關系的思想、等效的思想。

一、力和運動的思想

帶電體的運動情況取決于它的受力情況及初始狀態，準確分析帶電體的受力情況是解題的前提。帶電體所受的合力與初速度之間的關系是判斷帶電體的運動性質及運動軌跡的依據。從力和運動的角度進行分析是解決帶電體在電場中運動問題的最基本的方法。

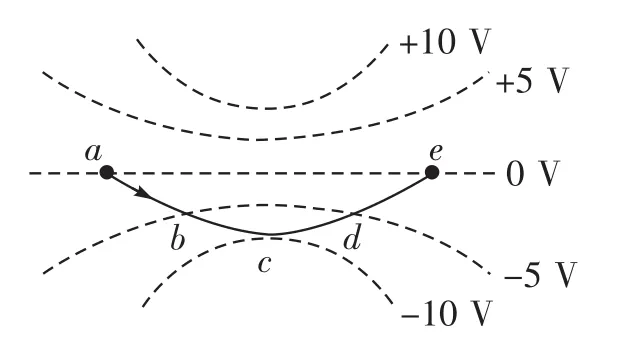
例1 （多選）對于由兩個固定的等量異種點電荷形成的電場，其等勢面如右圖中虛線所示。一帶電粒子以某一速度從圖中a點進入電場，其運動軌跡如圖中實線所示。若粒子只受靜電力作用，則下列關于帶電粒子的判斷正確的是（ ）。

A.帶正電

B.速度先變大后變小

C.電勢能先變大后變小

D.經過b點和d點時的速度大小相同

解析 根據等勢面的分布，我們可以畫出電場中的電場線。已知兩點電荷是等量異種電荷，則上面是正電荷，下面是負電荷，再根據粒子的運動軌跡及帶電粒子的受力指向軌跡凹側可知粒子帶負電，選項A錯誤。粒子從a到c再到e的過程中，電場力先做負功后做正功，粒子速度先減后增，電勢能先增大后減小，選項B錯誤，C正確。因為b、d兩點在同一等勢面上，所以粒子在b、d兩點的電勢能相同，即經過b點和d點時的速度大小相同，選項D正確。

故選CD。

二、分解的思想

帶電體處在電場或電場與重力場的復合場中，若其運動既非類平拋運動，又非圓周運動，而是一般的曲線運動，則在處理這類比較復雜的問題時，巧用運動的分解思想，可使問題得到快捷的解決。

例2 如右圖所示，在電場強度為E的勻強電場中（電場線水平，方向未標出），有一個質量為m、帶電量為-q的微粒（重力不計）。它在A點的瞬時速度為v，方向與電場線垂直，在B點的速度為2v。求：

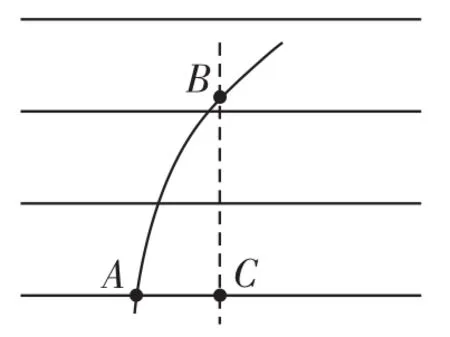
（1）A、B兩點的電勢差。

（2）微粒由A到B所花的時間。

解析 （1）根據微粒的運動軌跡可以判斷，微粒受到的電場力水平向右，電場方向應該是由C指向A。

（2）微粒在豎直方向上做勻速直線運動，在水平方向上做勻加速直線運動。可根據水平方向上的分運動求出時間。

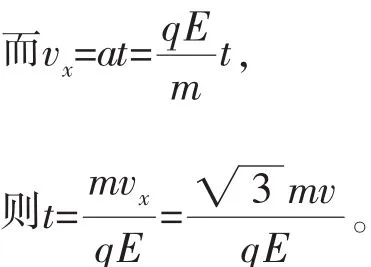
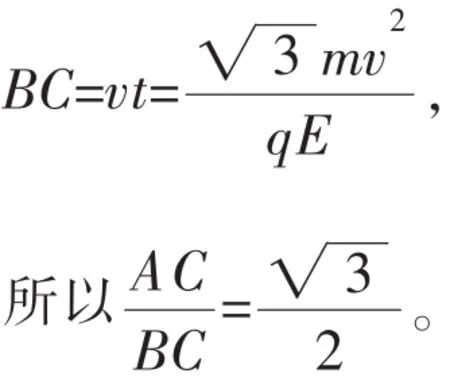
三、功能關系的思想

帶電體在電場中運動的過程中伴隨著做功和各種能量的轉化，由于電場力做功與路徑無關，這給動能定理和能量守恒定律的運用提供了廣闊的舞臺，特別是在曲線（有折返）運動中，更能體現能量觀點的優越性。

例3 如右圖所示，a、b、c三條虛線為電場中的等勢面，等勢面b的電勢為零，且相鄰兩個等勢面間的電勢差相等，一個帶正電的粒子在A點時的動能為10 J，在電場力F作用下從A運動到B后速度變為零。當這個粒子的動能為7.5 J時，其電勢能為（ ）。

A.12.5 J B.2.5 J C.0 D.-2.5 J

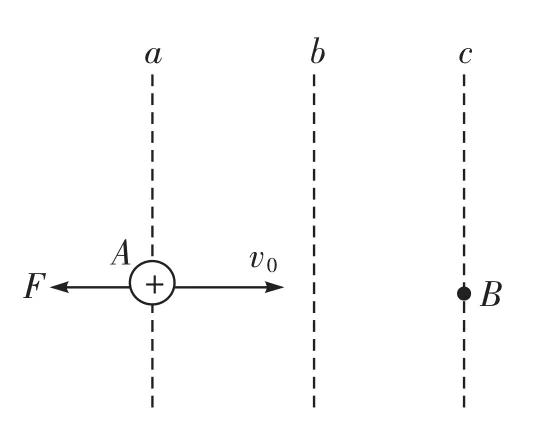
解析 由動能定理可知，帶電粒子到達等勢面b時的動能為5 J，帶電粒子只受電場力作用，動能與電勢能之和保持不變。由于等勢面b的電勢為零，即帶電粒子在等勢面b上時的電勢能為零，可得Ek+Ep=5 J，由此可以推知，當Ek=7.5 J時，Ep=-2.5 J。

故選D。

四、等效的思想

處在勻強電場中的帶電體除了受到電場力外，一般還會受到重力的作用。這類問題運用等效重力法，即將重力和電場力的合力看成一與重力等效的力，然后運用類比法，通常都能較簡捷地解決問題。運用等效的思想對物理過程進行分析，不僅便于我們對物理問題進行解答，而且對于靈活運用知識，促進知識和能力的遷移，都有很大的幫助。

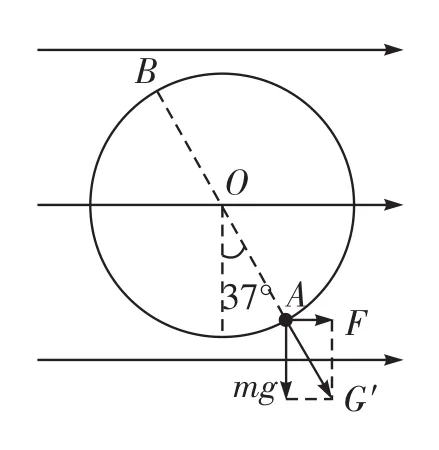
例4 水平向右的勻強電場中，用長為R的輕質細線在O點懸掛一質量為m的帶電小球，小球靜止在A處，A、O的連線與豎直方向夾角為37°。現給小球施加一個沿圓弧切線方向的初速度v0，小球便在豎直面內運動。為使小球能在豎直面內完成圓周運動，這個初速度v0至少應為多大？已知。

從以上幾例可以看出，力和運動的思想、分解的思想、功能關系的思想及等效的思想是解決電場中運動問題的有力武器。可以說解決這類問題的方法是一樣的，“萬變不離其宗”，我們可以融會貫通地理解，舉一反三地應用，養成歸納總結的良好習慣，以提高我們的物理素養。