“數學思想”在高中數學解題中的應用探微

徐春華●

江蘇省鹽城市田家炳中學 (224001)

?

“數學思想”在高中數學解題中的應用探微

徐春華●

江蘇省鹽城市田家炳中學 (224001)

在高中數學中，數學思想是數學知識以及數學方法的一種本質體現.數學方法是依據數學問題有效體現數學思想的一種重要手段和工具，數學思想是學生宏觀把握數學問題的一種能力.不斷加強數學思想方面的鍛煉可以更高效地幫助學生去理解復雜的數學題目，而且數學思維還可以靈活的進行轉變，從而達到事半功倍的效果.因此，主抓數學思想的教學對提高學生綜合解題能力的培養發揮著極其重要的作用.

1.高中數學中數形結合的思想

數形結合是指根據數學題目中給出的條件以及結論之間的關系，通過圖形將其體現，巧妙地得出解題的思路和方法，進而將問題化難為簡.

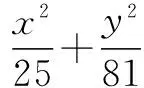
分析 在高中數學中，經常會出現這種類型的題目，將所求的內容限定在一定的條件下求極值問題.如果僅僅只用函數的知識去求解很難得出答案，此時，可以借助數形結合的思想，將該種問題轉變成坐標軸上直線截距的問題.令y-2x=b，則y=2x+b.結合圖形將問題轉化為在該橢圓上求一點P，使得直線過該點，且在y軸上有最大和最小截距.

經分析知：當直線與橢圓相切時，可以得到最大、最小截距.因此，可列方程

y=2x+b(1)；

將方程(1)和(2)聯立得

180x2+100xb+25b2-2025=0

由Δ=0可得

10000b2-4×180×(25b2-2025)=0

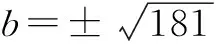
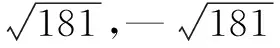
2.分類討論的數學思想

分類討論是指遵照一定的標準將所研究的內容分成幾個部分進行討論.其中最重要的是在分類討論過程中要對其正確劃分，不要漏掉討論的內容.

分析 比較兩者大小，一般是作差或者是作商，但是題中含有字母，可知需要將其分類討論，才能得出結果.

分類討論：

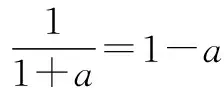
3.高中數學中的轉化思想

化歸思想是指在探究和解決有關數學問題時采用某種方法將問題通過變換使之轉化，進而達到解決的一種方法.

比如，有這樣一道題：A、B、C三個人投籃，每個人投籃成功的概率都是0.4，問至少有一人投籃成功的概率是多少？

分析 單純從這個題面上理解，至少有一人投籃成功包括以下三種情況，一是只有一個人投籃成功；一是有兩人投籃成功；最后一種是三人均投籃成功.但是依照這樣的思路進行解題，不僅復雜，還容易出錯.因此，可以將該問題轉化成“沒有人投籃成功的概率是多少”.

解P=1-(1-0.4)(1-0.4)(1-0.4)=0.784所以，至少有一人投籃成功的概率是0.784.

高中數學中，除以上三種類型外，還有幾大數學思想，在此不一一贅述，這些思想的宗旨在于幫助學生更好的理解和掌握數學精髓，然后更高效的完成解題.此外，通過對數學思想的掌握，還可以加強學生的思維發散、靈活變通的能力，進而不斷優化學生的思維，對提高學生的學習效率發揮著重要的作用.

G632

B

1008-0333(2016)28-0052-01