城市軌道交通網絡脆弱性分析

曲迎春，徐仲之，龔航，黃智仁，王璞

(中南大學 交通運輸工程學院，湖南 長沙 410075)

?

城市軌道交通網絡脆弱性分析

曲迎春，徐仲之，龔航，黃智仁，王璞

(中南大學 交通運輸工程學院，湖南 長沙 410075)

城市軌道交通網絡是城市公交系統的重要組成部分。以北京地鐵和深圳地鐵為研究對象，建立兩個城市的軌道交通網絡模型，利用兩個城市的地鐵乘客刷卡數據，估計城市軌道交通需求OD；基于復雜網絡理論分析兩個城市軌道交通網絡的拓撲結構，提出城市軌道交通網絡脆弱性的評價指標；建立城市公共交通雙層網絡，對城市軌道交通網絡的脆弱性進行更深層次的分析。研究結果表明:北京市與深圳市軌道交通網絡脆弱邊地理分布很相似，深圳市軌道交通網絡平均而言更加脆弱；軌道交通網絡的脆弱性與其網絡復雜度密切相關；城市常規公交網絡可以降低城市軌道交通系統的脆弱性。

地鐵乘客刷卡數據；軌道交通網絡；OD估計；脆弱性

隨著我國小汽車保有量的快速增長，城市交通擁堵日趨嚴重，很多城市的交通管理部門都開始鼓勵市民使用公共交通出行。城市軌道交通速度快、運量大，是公共交通系統的骨架。然而，城市軌道交通系統結構日趨復雜、運載量不斷增大，故障、自然災害等突發情況會對軌道交通系統造成嚴重威脅[1-3]。例如：2011年12月22日北京地鐵1號線突發信號故障，導致列車中斷運營1 h；2014年5月4日南京地鐵4號線九華山基站坑發生滲水事故，造成北京東路九華山段由東向西交通一度中斷；2015年7月28日上海地鐵1號線錦江樂園至徐家匯方向突發供電故障，造成大量乘客滯留。城市軌道交通系統的可靠性是關系人民生活和社會經濟發展的重要問題，受到了科學與工程領域學者的廣泛關注[4-7]。

利用復雜網絡理論與統計學方法，很多學者對城市軌道交通網絡的拓撲結構進行了深入研究。高潔等[8]根據城市軌道交通網絡受到外界攻擊后運營能力的改變，定義了城市軌道交通網絡系統抗毀可靠性，將站點子系統和區間子系統受到破壞后對客流量的影響作為評價依據。王志如等[9]選取最大連通OD數目、路徑長度以及乘客換乘次數作為地鐵網絡脆弱性的評價指標，在仿真模型中分別對地鐵車站和區間線路進行隨機攻擊和蓄意攻擊，發現車站在蓄意攻擊時具有脆弱性，區間線路在蓄意攻擊時具有魯棒性。張建華等[10]對上海市軌道交通網絡的連通性和魯棒性進行了研究，分析了單條地鐵線上的站點受到攻擊時地鐵網絡的連通性，發現介數較大的站點受到攻擊時對網絡的影響較大。孫劍等[11]對上海市軌道交通網絡換乘站點的脆弱性進行分析，建立了基于客流量的換乘站點脆弱性的綜合評價指標模型，定位了10個最脆弱的換乘車站。鄧勇亮等[12]驗證了南京地鐵網絡既具有小世界屬性也具有無標度屬性，并利用全網效率和平均最短路徑來度量網絡的脆弱性，結果顯示南京地鐵網絡在隨機攻擊下表現了較強魯棒性，但在刻意攻擊下卻很脆弱。

本文首先建立北京市和深圳市的軌道交通網絡模型，利用北京市和深圳市的地鐵乘客刷卡數據，估計了早高峰軌道交通需求OD；然后，分析現階段兩個城市軌道交通網絡的拓撲結構，研究了軌道交通站間區間故障對乘客出行可達性及出行時間的影響；最后，基于深圳市地鐵網絡和公交網絡建立了城市公共交通雙層網絡模型，更精確地評價了軌道交通網絡的脆弱性。

1 城市軌道交通網絡拓撲建模及OD估計

北京市和深圳市的軌道交通網絡具有不同的拓撲結構特征。本文提出了兩個脆弱性評價指標，對兩個城市軌道交通網絡的脆弱性進行分析，分析了兩個軌道交通網絡脆弱性的共性規律和異同特征，挖掘軌道交通網絡脆弱性和網絡結構間的關系。表1是北京地鐵和深圳地鐵的一些基本信息。

表1 北京地鐵和深圳地鐵的基本信息表

1.1 城市軌道交通網絡拓撲建模

結合圖論中有向圖模型，將城市交通網絡抽象為由節點和連邊構成的有向圖G=(V,E)，集合V中的元素為圖G的節點集合，集合E中的元素為圖G的邊(線)集合，集合E中的元素由集合V中的任意兩點連接產生。在城市軌道交通網絡中，節點表示城市軌道交通車站，有向邊表示城市軌道交通網絡的站間區間。

本文利用Google Earth軟件采集地鐵站點的經緯度坐標，根據站點間的空間拓撲關系構建了北京市和深圳市的軌道交通網絡(圖1(a) & (b))。北京市軌道交通網絡包含228個節點、507條邊，深圳市軌道交通網絡包含118個節點、252條邊。根據軌道交通運營時刻表，我們計算了各個站間區間的運行時間，用于表示邊的權重。為了更加準確地計算乘客出行時間，我們還收集了不同線路間的換乘時間信息。

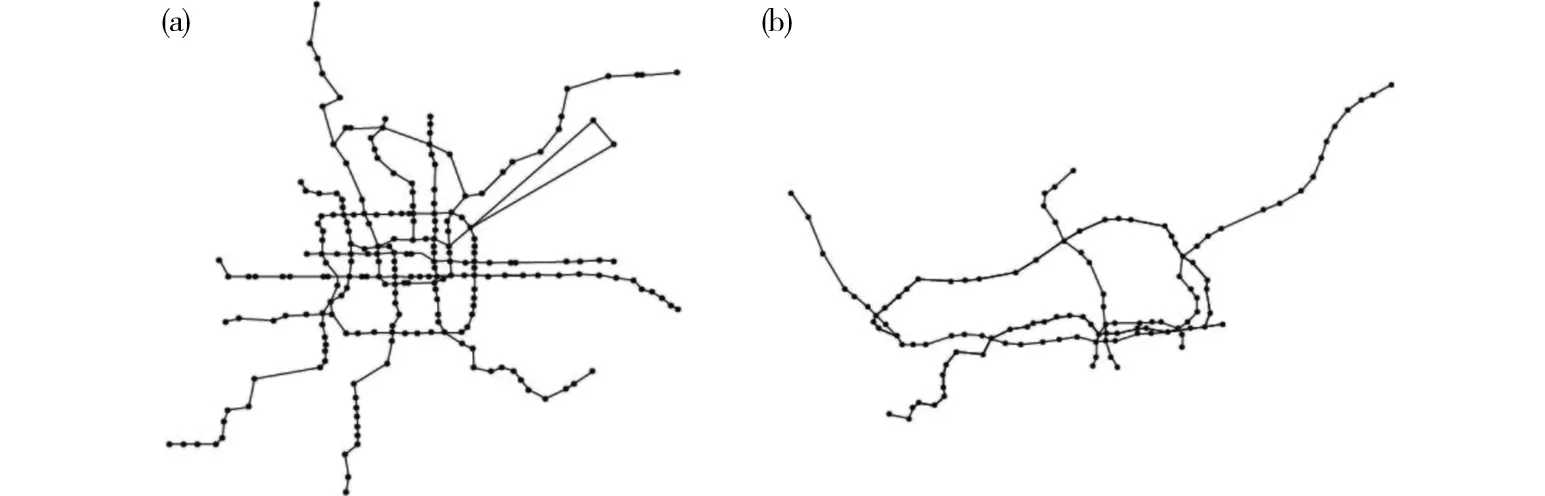
(a)北京市軌道交通網絡;(b)深圳市軌道交通網絡圖1 城市軌道交通網絡Fig.1 Urban rail transit network

1.2 軌道交通出行OD估計

本文使用北京市和深圳市某工作日的地鐵乘客刷卡數據估計軌道交通出行OD，乘客刷卡數據記錄了乘客編號、進站時間與站點、出站時間與站點。北京市和深圳市的乘客刷卡量呈現雙駝峰分布(圖2(a)和(b))，早高峰(8:00～9:00)和晚高峰(18:00～19:00)的出行量明顯高于其他時段的出行量。本文選取早高峰時段為研究時段。

篩選早高峰(8:00～9:00)使用地鐵出行的乘客刷卡記錄，這些出行記錄分為4種類型：1)8:00以后出發，9:00之前到達；2)8:00之前出發，9:00之前到達；3)8:00以后出發，9:00以后到達；4)8:00之前出發，9:00以后到達。類型1出行的進站時間和出站時間均在8:00～9:00之內，出行起點(O)與出行終點(D)不變。對于類型2、3、4，計算乘客起終點之間的最短路徑，選擇在8:00～9:00第一次和最后一次經過的站點作為新的出行起點(O)和出行終點(D)，從而獲得的北京市和深圳市軌道交通網絡在早高峰時段的出行需求OD分布，兩市軌道交通早高峰時段出行總量分別為：2 113 378人次，203 882人次。

(a)北京市時變交通需求;(b)深圳市時變交通需求圖2 時變交通需求Fig.2 Time-varying passenger volume

2 城市軌道交通網絡的拓撲結構分析

2.1 節點度

復雜網絡中節點度ki定義為與節點直接相連的邊的數目，節點度的大小也表征了網絡中各節點的中心性，其平均值在一定程度上反映了整個網絡拓撲結構的連接復雜度，是網絡結構特征最直接的度量[14]，節點度的計算如公式(1)所示：

(1)

式中：aij表示節點i與節點j之間是否存在邊，若存在，則aij=1，否則aij=0；

北京市和深圳市的軌道交通網路站點的度分布如圖3a，兩個城市軌道交通網絡80%以上的站點度為2，大部分站點為非換乘站點，平均節點度分別為2.23和2.13，節點度大于3的站點占比分別為14.9%和11%，最大度分別為5和4。從節點度計算結果來看，北京市軌道交通網絡的復雜度高于深圳市軌道交通網絡的復雜度，度值較大的節點占比較高。

2.2 邊介數中心度

復雜網絡中的邊介數中心度bc定義為網絡中所有最短路徑中經過該邊的路徑的數目占最短路徑總數的比例，反映了邊在整個網絡中的拓撲重要程度[15]。邊介數中心度的計算如式(2)所示：

(2)

式中：σst表示任意兩節點s和t之間的最短路徑總數；σst(v)表示最短路徑中通過邊v的次數。

北京市和深圳市的軌道交通網絡的邊介數中心度都近似服從高斯分布，如圖3(b)所示，北京：P(bc)=0.108 8e-((bc-0.028)/0.029)2，深圳：P(bc)=0.085 2e-((bc-0.047 5)/0.056 2)2。北京地鐵的平均邊介數中心度(0.029)小于深圳地鐵的平均邊介數中心度(0.054)。從邊介數中心度的分布情況來看，北京市軌道交通網絡邊的平均可替代性要高于深圳軌道交通網絡邊的平均可替代性。

2.3 最短路徑及平均最短路徑長度

最短路徑又稱為測地路徑，在加權有向網絡中兩個節點之間的最短路徑指連接這兩個節點的邊的權值之和最小的路徑，最短路徑長度指兩個節點的最短路徑上的邊的權值之和。平均最短路徑長度L定義為任意兩個節點之間的距離的平均值，計算式如(3)所示：

(3)

式中：L表示網絡節點數；dij表示任意節點i與節點j之間的最短路徑長度。

北京市和深圳市軌道交通路網中的邊權重為相鄰站間區間的運行時間，網絡中最短路徑長度即為兩個車站最短路徑間的運行時間之和，單位為分鐘。經測量，北京市與深圳市的軌道交通網絡的最短(時間)路徑長度分布服從高斯分布(圖3c)，北京:P(L)=0.116 6e-((L-34.53)/29.88)2，深圳P(L)=0.128 8e-((L-28.66)/27.19)2，平均最短(時間)路徑長度分別為38.5 min和32 min。盡管北京市軌道交通網絡的覆蓋范圍比深圳市軌道交通網絡大很多，但其平均最短(時間)路徑長度僅增加6.5 min，說明北京市軌道交通網絡的可達性較高。

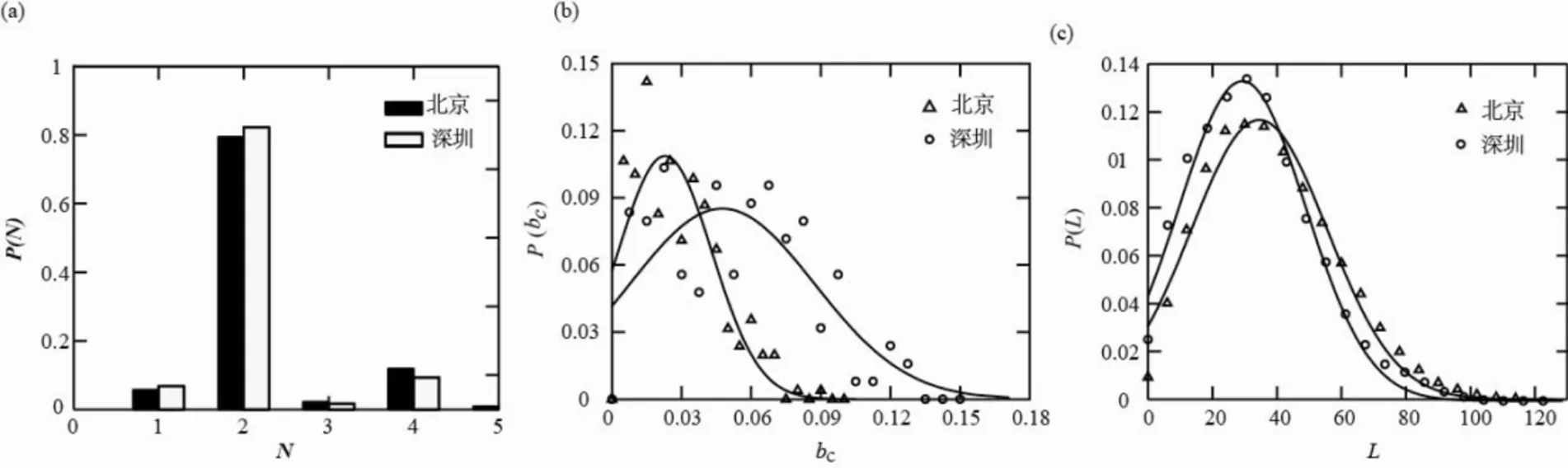
(a)節點度分布；(b)邊介數中心度分布；(c)最短路徑長度分布圖3 軌道交通網絡拓撲結構屬性Fig.3 Topological properties of the urban rail transit networks

基于以上分析可知，北京市軌道交通網絡的網絡復雜度較高，邊可替代性也較高。北京地鐵和深圳地鐵分別代表了軌道交通網絡拓撲結構發展的兩個階段，北京市的軌道交通網絡結構較為成熟，具有更強的網絡可達性和連通性。

3 城市軌道交通網絡的脆弱性分析

脆弱性指受事件影響而導致服務水平下降的敏感系數。在交通網絡科學的相關研究中，城市軌道交通網絡的脆弱性定義為不同站間區間(或站點)失效而影響軌道交通網絡全局效率的大小。本文分析了城市軌道交通網絡站間區間失效對乘客出行可達性及出行時間的影響。

利用Dijkstra算法,將早高峰交通需求OD按最短路徑分配到軌道交通路網，統計了站間區間的客流量[16]。圖4數據顯示網絡中的客流量分布不勻，少部分區間客流量很大，而大部分區間客流量相對較小。

3.1 出行失敗率

首先，我們定義了站間區間故障導致的出行失敗率fr，即軌道交通站間區間故障時，不能到達目的地的出行數占總出行數的比例，用于評估軌道交通站間區間的脆弱性(式4)。

(4)

式中:fr(v)是指站間區間v發生故障時的出行失敗率；N為出行總量；ai(v)為站間區間v故障時，第i個出行是否失敗，如果出行失敗，則ai(v)=1，否則ai(v)=0。

圖5展示了站間區間出行失敗率fr的分布，兩個城市軌道交通網絡站間區間的出行失敗率fr均服從指數分布，北京：P(fr)=0.730 4e-386.7fr(R2=0.991)，深圳：P(fr)=0.690 8e-137.8fr(R2=0.992)。出行失敗率fr較高的區間均分布在地鐵網絡邊緣，而中心環線的站間區間出行失敗率偏低。造成這一現象的原因為分布在地鐵網絡邊緣的線路多為單線路，一旦發生故障很難找到替代線路，必然導致經過此線路的出行不能完成。

雖然兩個城市站間區間出行失敗率分布基本一致(均服從指數分布)，但北京市軌道交通網絡站間區間的平均出行失敗率明顯低于深圳市軌道交通網絡，北京市的最高出行失敗率fr只有0.04，而深圳市的最高出行失敗率fr超過0.1。分析這一現象的原因是兩個軌道交通網絡的結構復雜度不同，北京地鐵站形成的回路較多，多數出行可以找到替代線路。

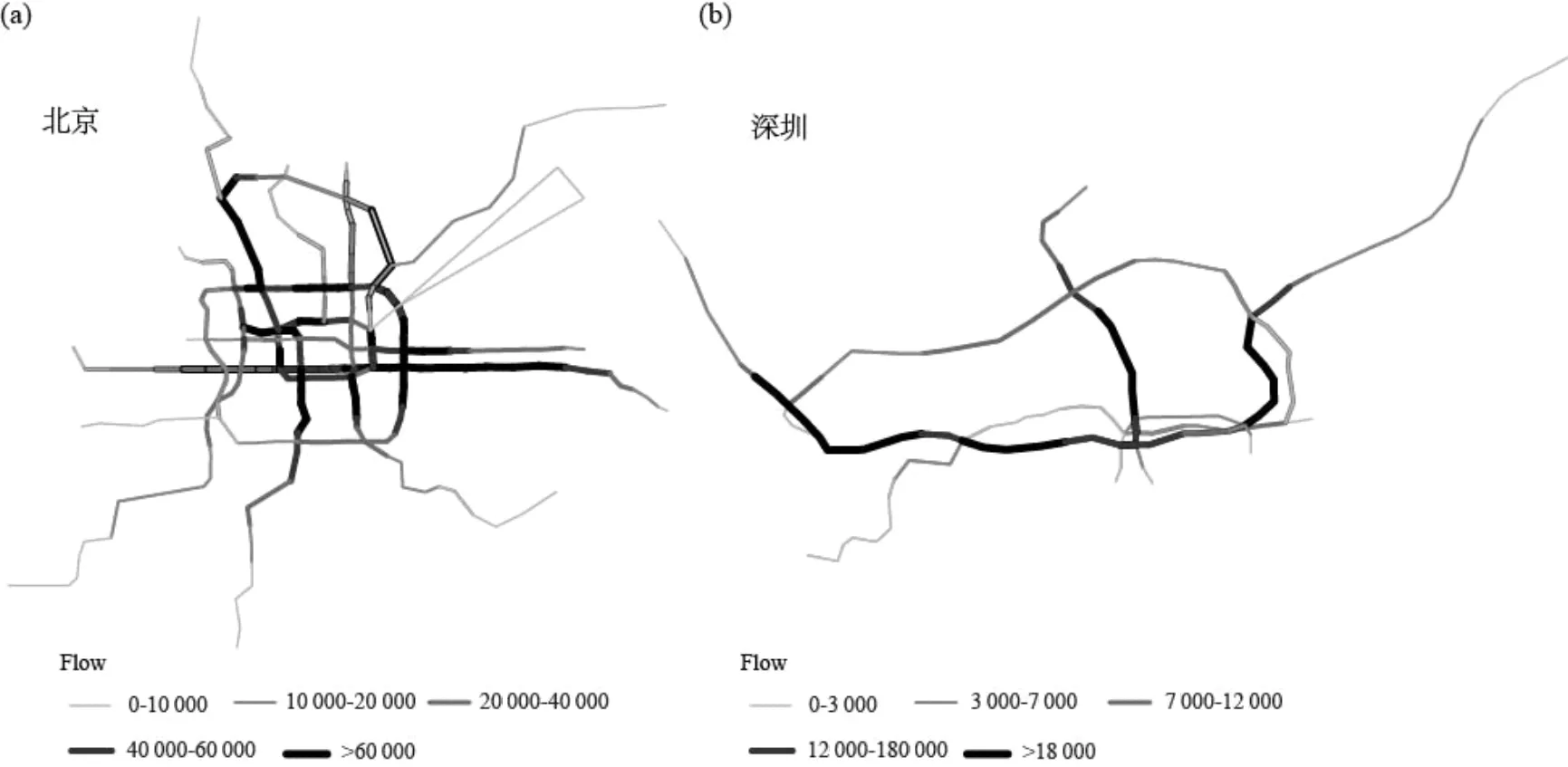
(a)北京市軌道交通客流量分布；(b)深圳市軌道交通客流量分布圖4 軌道交通網絡客流量分布Fig.4 Distribution of passenger flow inurban rail transit networks

3.2 出行時間增加率

擁有替代線路的站間區間一般位于環線上，當此類站間區間出現故障時，因為存在替代路徑，因此出行失敗率較低。但這種情況下，乘客由于需要繞路，出行時間大大增加。為了量化這一影響，我們定義了站間區間故障時造成的總出行時間增加率tr，即軌道交通發生故障時，乘客通過改變出行路徑到達目的地，其增加的出行時間占總出行時間的比例(式5)。

(5)

式中：tr(v)是指站間區間v發生故障時的出行時間增加率；ti為未發生故障時第i個出行所用的出行時間；ti(v)為站間區間v發生故障時，第i個出行的出行時間。

研究發現：兩個城市的軌道交通網絡出行時間增加率tr較大的站間區間在空間上基本分布在環線(圖5(a)和5(b))，兩個城市軌道交通網絡站間區間的出行時間增加率近似服從指數分布(圖5(d))，北京：P(tr)=0.447 5e-214tr(R2=0.979)，深圳：P(tr)=0.512 7e-77.62tr(R2=0.965)。表明城市地鐵網絡站間區間發生故障時，出行時間增加率的概率分布相似。

但是，由于兩個軌道交通網絡的網絡復雜度不同，出行時間增加量存在一定差異，深圳地鐵的出行時間增加率明顯高于北京地鐵，北京市最大tr僅為0.059，而深圳市最大tr達到了0.24(圖5(d))。即當該站間區間發生故障時，總出行時間增加24%，導致軌道交通網絡效率大幅下降。

為了進一步研究城市軌道交通網絡脆弱邊對網絡效率的影響，我們分析了脆弱邊發生故障時，其它站間區間客流量的變化。選取北京市與深圳市出行時間增加率最大的站間區間，分別為北京地鐵13號線知春路到五道口部分、深圳地鐵羅寶線深大到桃園部分(圖6)。研究發現當上述兩個站間區間發生故障時，很多乘客需要選擇最近環線繞行，環線客流量平均增加3倍和5倍，最大客流增加量分別為正常情況的7倍和6.6倍。

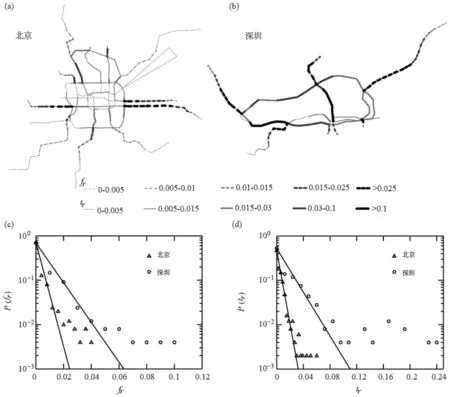
(a)北京出行失敗率；(b)深圳出行失敗率；(c)北京出行時間增長率；(b)深圳出行時間增長率圖5 出行失敗率分布與出行時間增長率分布Fig.5 Distribution of trip failure rate and distribution of trip time increasing rate

(a)北京地鐵客流量增長率分布；(b)深圳地鐵客流量增長率分布圖6 軌道交通區間故障導致其它站間區間客流量增長Fig.6 Passenger volume increasing rate after removing the segment with largest trip time increasing rate

4 公共交通雙層網絡下的軌道交通網絡脆弱性分析

上述研究結果表明，當城市軌道交通線路發生故障時，不僅會導致大量出行失敗、總出行時間增加，還會導致某些站間區間的客流量突增。然而，上述分析結果是建立在城市僅有軌道交通網絡的基礎上的，實際上大城市都有比較完善的常規公交系統。為了更精確地分析軌道交通網絡的脆弱性，我們以深圳為例，建立公共交通雙層網絡分析軌道交通故障對乘客出行帶來的影響。

4.1 城市公共交通雙層網絡的構建

如果常規公交站點與軌道交通站點之間的距離小于500 m，則在它們之間搭建換乘邊，進而構建由常規公交網絡與軌道交通網絡組成的城市公共交通雙層網絡。兩層網絡的換乘時間按步行時間計算，取均值為5 min。深圳市常規公交網絡包含9 114個站點、17 119條邊，與地鐵站點距離在500 m以內的站點數量為1 197。深圳市城市公共

交通雙層網絡如圖7所示，共包括9 232個站點，19 865條邊，其中換乘邊有2 394條。

圖7 深圳市公共交通雙層網路Fig.7 Two-layer public transportation networkof Shenzhen

4.2 城市公共交通雙層網絡中軌道交通路段脆弱性分析

本文依次計算了城市公共交通雙層網絡中每一個軌道交通站間區間發生故障時的出行失敗率fr和出行時間增加率tr。考慮公交網絡層后，出行失敗率fr=0，平均出行時間增加率也大幅度降低，從僅考慮單層軌道交通網絡時的3%降到了1.5%(圖8(d))。

(a)流量分布；(b)、(c)流量減少分布；(d)出行時間增加率分布圖8 城市公共交通雙層網絡流量分布，出行時間增加率分布Fig.8 Distribution of passengers volume and distribution of trip time increasing rate in Two-layer public transportation network

仍以出行時間增加率最大的深大站到桃園站區間為例，分析此站間區間故障時其它站間區間的流量變化(圖8(a)和8(c))，8(a)為該區間故障時，城市公共交通雙層網絡中軌道交通層的客流量變化。8(b)和8(c)為該區間故障時，城市公共交通雙層網絡中軌道交通層比僅考慮軌道交通網絡時的站間區間流量減少率fmi分布。

仿真結果表明軌道交通網絡發生故障時，公交層可以分擔大量流量，緩解軌道交通網絡層客流量突增。軌道交通網絡層的流量分布(圖8(a))與未發生故障時的流量分布(圖4(b))相近，乘客總出行時間僅比未發生故障時增加8.4%。而僅考慮單層城市軌道交通網絡時，總出行時間增加24%。因此，常規公交網絡對于降低城市軌道交通系統脆弱性具有很重要的作用。

5 結論

1)本文利用北京和深圳兩個城市的大規模地鐵刷卡數據，對兩個軌道交通網絡的脆弱性分別從出行失敗率，出行時間增加率和其它站間區間客流增量三個分面做了較深入的測量和分析。研究結果表明：兩城市脆弱性指標既具有相同的概率分布，又在數值上有較大差異。脆弱性的相似特征源于兩城市地鐵客流分布的相似性，而脆弱性的異同特征則可以從軌道交通網絡的復雜度解釋。

2)相比以前僅利用軌道交通網絡本身分析其脆弱性，本文構建城市公共交通雙層網絡,考慮了常規公交對軌道交通故障的緩沖作用。我們發現常規公交網絡可以在軌道交通網絡發生故障時，大幅降低出行失敗率和出行時間增加率，避免了軌道交通客流突增。

[1] Nguyen T P K, Bdugin J, Marais J. Method for evaluating an extended Fault Tree to analyse the dependability of complex systems: Application to a satellite-based railway system[J]. Reliability Engineering & System Safety, 2015, 133: 300-313.

[2] Cadrso L, Marín, Maróti G. Recovery of disruptions in rapid transit networks [J]. Transportation Research Part E: Logistics and Transportation Review, 2013, 53: 15-33.

[3] Vuchic V R. Urban Transit: Operations, Planning, and Economics [J]. Operations, 2005:45(:3).

[4] Derrible S, Kennedy C. The complexity and robustness of metro networks[J]. Physica A 2010, 389, 3678-3691.

[5] 韓豫, 成虎, 趙憲博, 等. 基于脆弱性的城市軌道交通運營安全理論框架[J]. 城市軌道交通研究, 2012(11):15-19. HAN Yu, CHENG Hu, ZhAO Xianbo, et al. Theoretic structure of urban mass transit operation safety based on vulnerability[J]. Urban Mass Transit. 2012(11):15-19.

[6] Angeloudis P, Fisk D. Large subway systems as complex networks [J]. Physica A: Statistical Mechanics and its Applications, 2006(367): 553-558.

[7] 鄧連波, 高偉, 賴天珍, 等. 基于換乘網絡的城市軌道交通關聯公交接駁線網優化[J]. 鐵道科學與工程學報, 2012, 9(6):77-83. DENG Lianbo, GAO Wei, LAI Tianzhen, et al. Optimal design of feeder-bus network related to urban rail transit based on transfer network [J]. Journal of Railway Science and Engineering, 2012, 9(6):77-83.

[8] 高潔, 施其洲. 城市軌道網絡抗毀可靠性定義及評價指標模型研究[J]. 鐵道學報, 2007, 29(3):29-33. GAO Jie, SHI Qizhou. Definition and evaluation modeling of metro network invulnerability [J]. Journal of the China Railway Society, 2007, 29(3): 005.

[9] 王志如, 李啟明, 梁作論. 城市地鐵網絡拓撲結構脆弱性評價[J]. 中國安全科學學報, 2013, 23(8):114-119. WANG Zhiru, LI Qiming, LIANG Zuolun. Evaluation of urban metro network topological structure vulnerability[J]. China Safety Science Journal, 2013, 23(8):114-119.

[10] ZHANG Jianhua, XU Xiaoming, LIU Hong, et al. Networked analysis of the Shanghai subway network, in China [J]. Physica A: Statistical Mechanics and its Applications, 2011, 390(23): 4562-4570.

[11] SUN Jian, ZHAO Yuhan, LU Qingchang. Vulnerability analysis of urban rail transit networks: A case study of Shanghai, China [J]. Sustainability, 2015, 7(6): 6919-6936.

[12] DENG Yongliang, LI Qiming, LU Ying, et al. Topology vulnerability analysis and measure of urban metro network: The case of Nanjing [J]. Journal of Networks, 2013, 8(6): 1350-1356.

[13] HE Kun, XU Zhongzhi, WANG Pu. A hybrid routing model for mitigating congestion in networks [J]. Physica A: Statistical Mechanics and its Applications, 2015(431): 1-17.

[14] WANG Junjie, LI Yishuai, LIU Jingyu, et al. Vulnerability analysis and passenger source prediction in urban rail transit networks[J]. PloS ONE, 2013, 8(11)1-8.

[15] Newman M E J. A measure of betweenness centrality based on random walks[J]. Social Networks, 2005, 27(1): 39-54.

[16] 王俊杰, 譚倩, 王璞. 城市軌道交通客流突增研究[J]. 鐵道科學與工程學報, 2015, 12(1):196-202. WANG Junjie, TAN Qian, WANG Pu. Analysis of surging passenger flow in urban rail transit network[J]. Journal of Railway Science and Engineering, 2015, 12(1):196-202.

Vulnerability analysis of urban rail transit networks

QU Yingchun, XU Zhongzhi, GONG Hang, HUANG Zhiren, WANG Pu

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

The urban rail transit network is an important part of an urban public transportation system. First, we generated the network models of the urban rail networks of Beijing and Shenzhen. We used the subway smart card data to estimate the passenger travel demands in the two urban rail transit networks. Next, we analyzed the topological structures of the two urban rail transit networks based on complex network theory and proposed the indices to evaluate the vulnerability of an urban rail transit network. Finally, we generated a two-layer public transportation network to obtain a deeper understanding of the vulnerability of urban rail transit networks. Our empirical results show that the distribution of vulnerable segments is similar in Beijing and Shenzhen rail transit networks. Averagely, Shenzhen urban rail transit network is more vulnerable. The vulnerability of an urban rail network is highly related with its network complexity. Urban bus transit network can reduce the vulnerability of urban rail transit system.

subway smart card data; urban rail transit network; OD estimation; vulnerability

2016-01-11

國家自然科學基金資助項目(61473320)

王璞(1983-)，男，河北石家莊人，教授，博士，從事交通運輸規劃與管理、復雜網絡和數據挖掘方面的研究；E-mail: wangpu@csu.edu.cn

U231+.2

A

1672-7029(2016)11-2276-08