某大峽谷玻璃橋橋址邊坡穩定性分析

金書濱,胡濤,喬世范

(1．貴州省公路工程集團有限公司，貴州 貴陽 550008；2.中南大學 土木工程學院，湖南 長沙 410075)

?

某大峽谷玻璃橋橋址邊坡穩定性分析

金書濱1,胡濤1,喬世范2

(1．貴州省公路工程集團有限公司，貴州 貴陽 550008；2.中南大學 土木工程學院，湖南 長沙 410075)

為確保某大峽谷玻璃橋及配套工程建設的安全，基于有限元方法對大峽谷兩側陡立岸坡及拉錨處進行穩定性分析，并對最初設計時的橋址位置是否適宜建設該工程進行評價。采用三維有限元軟件，結合現場巖土工程條件，對玻璃橋橋址邊坡在天然狀態下和橋梁荷載條件下的位移、應力狀態進行數值模擬，獲得坡體在玻璃橋荷載作用下塑性區的分布規律。研究結果表明：所計算橋址的位置在外力作用下處于欠穩定—不穩定狀態，建議改變橋址設計位置或對不良地質作用發育區域的巖體進行加固治理，為某大峽谷玻璃橋的進一步設計提供參考。

邊坡穩定性分析；三維有限元；位移狀態；應力狀態；數值模擬

在山區峽谷地帶修建橋梁時，修建橋墩的位置不可避免的要位于峽谷兩岸的岸坡上，為了保證橋梁整體的安全性和穩定性，需要對橋基岸坡的穩定性進行驗算分析。與一般的邊坡不同，峽谷橋梁橋址邊坡往往坡度較陡，坡高較大，此外當岸坡巖體結構復雜且存在如巖性、水文條件等諸多不確定性因素的影響時，對其穩定性進行分析將會變得非常困難。

目前，對于邊坡穩定性的分析計算方法[1-4]有很多，主要有如下2類：一是經典的基于極限平衡理論的分析方法，二是采用數值模擬[5-6]方法(包括有限元法、離散元法等)進行邊坡穩定性分析。

孟慶文等[7]以某高速鐵路高邊坡為例，分別計算不同施工階段滑面為圓弧面和折線面、坡體無水和飽和等各種條件下邊坡的穩定性安全系數并分析了其影響規律。張利國等[8]以某鐵路客運專線橋基高邊坡為例，應用ANSYS有限元分析軟件，對荷載作用下的高邊坡巖體力學行為特征和穩定性進行了三維有限元分析，從安全系數角度分析了大橋邊坡的整體穩定性。彭富強等[9]依托婁新高速K22+200～K22+400段右側邊坡支護工程，應用有限元對邊坡進行了穩定性分析，并與現場監測點數據進行對比，驗證了有限元分析結果的可靠性。盧應發等[10]在現行滑坡穩定分析的基礎上，建立了推移式滑坡漸進破壞穩定性分析法，研究了有限元滑坡穩定計算的特點，分析了引起滑坡有限元法計算不收斂的原因，提出了滑坡有限元計算的滑面邊界法。上述相關學者的研究表明，應用有限元法分析計算邊坡的穩定性是可靠有效的。

本文以某大峽谷玻璃橋橋址邊坡為例，運用有限元分析軟件ABAQUS計算大峽谷兩側陡立岸坡及拉錨處的穩定性，模擬橋址邊坡在天然狀態下和橋梁荷載條件下的位移場、應力場狀態，并基于數值模擬結果對橋址處修建玻璃橋的適宜性進行評價。

1 工程概況

某大峽谷籌建的玻璃橋，位于湖南省某大峽谷景區內，是世界上最高、跨度最長的玻璃橋。大橋建在大峽谷兩側的絕壁峰頂之上，橫跨整個大峽谷，橋拱距谷底的相對高度約250 m，橋寬6 m，橋長約370 m，橋面全部采用透明玻璃鋪設，橋中心設有全球最高蹦極臺。

1.1 場地位置及地形地貌

該玻璃橋東西兩側橋墩分別位于湖南省的某大峽谷陡立岸坡兩側，場地原始地貌單元為巖溶(喀斯特)地貌中的峰林地形，勘察期間，測得場地各鉆孔孔口標高變化于581.38～608.00 m之間。場地內主要以垂直巖溶發育為主，地表出露串狀落水洞，各落水洞之間存在一的聯系，溶洞及節理裂隙以垂直發育為主。

1.2 場地構造

根據工程地質測繪和調查結果，西側橋墩場地西南側巖層局部發育有揉皺及巖層小錯動現象。其具體情況如圖1所示。

圖1 西側橋墩場地西南側巖層小錯動照片Fig.1 Figure of west pier site southwest rock rupture

根據本次工程地質測繪和調查結果，該玻璃橋東西兩側橋墩場地內微風化灰巖節理裂隙發育，在微風化灰巖露頭節理裂隙發育地段進行了節理裂隙統計并繪制了節理玫瑰花圖，見圖2。根據節理玫瑰花圖可見：灰巖產狀為，傾向介于300°～338°，傾角介于12°～35°，傾角由西向東(大峽谷方向)逐漸變緩，場地主要發育兩組節理裂隙，如圖2所示。第一組節理裂隙傾向介于150°～180°，傾角介于78°～87°，第二組節理裂隙傾向介于60°～90°，傾角介于75°～85°，這兩組節理為X節理；某大峽谷玻璃橋東側橋墩場地：灰巖產狀為，傾向介于142°～175°，傾角介于10°～36°，傾角由東向西(大峽谷方向)逐漸變緩，場地主要發育兩組節理裂隙，第一組節理裂隙傾向介于240°～270°，傾角介于79°～86°，第二組節理裂隙傾向介于320°～350°，傾角介于75°～85°，這兩組節理為X節理。

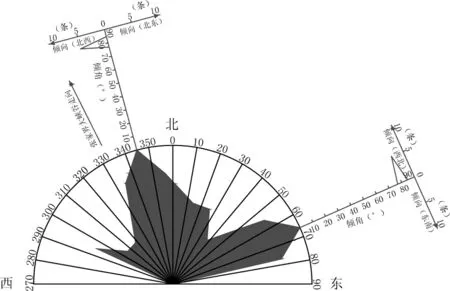
圖2 東側橋墩場地節理玫瑰花圖Fig.2 Joint rose figure of east pier site

1.3 地層巖性

據鉆探揭露，場地地層自上而下依次由植物層、第四系坡積層、三疊系(T)微風化灰巖等組成．各地層的野外特征分述如下：

1)植物層(Q4pd)：褐黃色，主要由粘性土組成，含植物根莖，呈松散狀態。

2)第四系坡積(Qdl)粉質黏土：褐黃色，切面稍有光澤，搖震無反應，韌性、干強度中等，呈可塑狀態。發育有石牙，即微風化灰巖，揭露的視厚度為0.30～2.00 m。

3)三疊系(T)微風化灰巖：灰青色，灰白色，中厚層狀構造，主要礦物成分為方解石，長石等礦物，節理裂隙較發育。在該層中發育有3個亞層，即巖溶充填物、溶蝕裂隙及溶洞。

1.4 場地穩定性及適宜性評價

該玻璃橋及配套工程選擇大峽谷兩側陡立岸坡附近位置，橋梁類型為拉索橋。為確保該玻璃橋及配套工程建設的安全，現對大峽谷兩側陡立岸坡及拉錨處進行穩定性分析，并對最初設計時的橋址位置是否適宜建設該工程進行評價。

2 有限元計算方法與理論

2.1 本構模型的選擇

數值計算采用有限單元法，采用大范圍的三維有限元計算。

采用了大型非線性有限元計算軟件ABAQUS程序進行三維有限元分析計算。

根據工程實際情況，巖土體采用彈塑性材料，選用Mohr-Coulomb準則，見圖3。

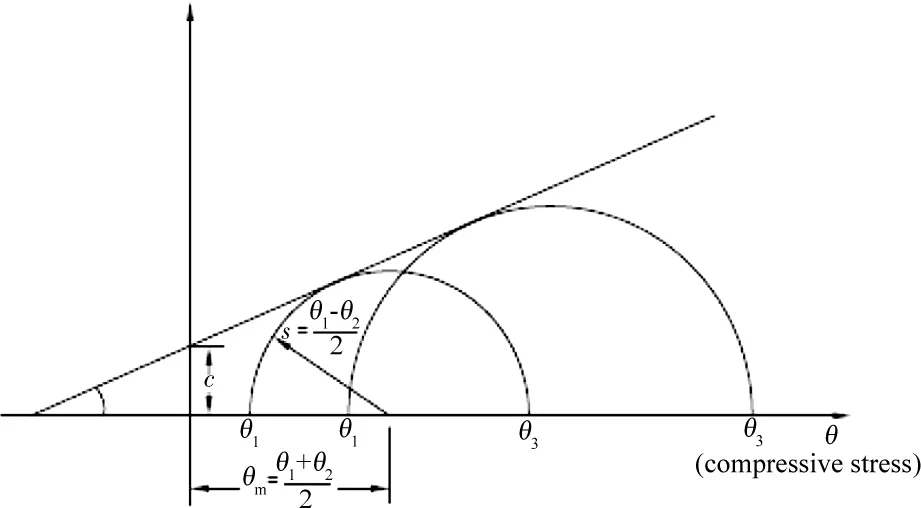
圖3 Mohr-Coulomb屈服模型Fig.3 Mohr-Coulomb yield model

Mohr-Coulomb模型的彈性階段必須是線性、各向同性的，其屈服函數為：

F=Rmcq-ptanφ-c=0

(1)

其中Rmc(θ,φ)為π平面上屈服面形狀的一個度量。

其中φ為巖土材料的摩擦角，0≤φ≤90°；C為巖土材料的黏聚力；θ為極偏角。

在Mohr-Coulomb模型中，實質上假定了由黏聚力系數來確定其硬化。

利用使用Abauqs中所提供的Mohr-Coulomb模型求解巖土工程問題，應注意的問題如下：

1)由于Mohr-Coulomb模型的塑性流動法則是非關聯的，因此必須來用非對稱求解器。

2)由于Mohr-Coulomb模型在使用前必須進行標定，其典型的標定方法是從若干個不相同的三維試驗中獲得極限應力狀態，并把它們定位于子午線平面上來估算摩擦角與黏聚力C。因此，必須慎重確定膨脹系數。

3)由于在ABAQUS中，Mohr-Coulomb模型采用的是光滑塑性流動勢面，它不同于經典的相關聯的Mohr-Coulomb準則的流動勢面(它是由若干個平面形成的折面組成)。因此，ABAQUS中的Mohr-Coulomb模型中的塑性行為與經典的Mohr-Coulomb模型有所不同。

2.2 初始地應力場的計算方法

在進行開挖的模擬計算時，初始地應力場[11]是隨后迭代計算的基礎，只有采用與實際相符的初始地應力場，才可能得出真實的解答。初始地應力場指的是玻璃橋修建前峽谷崖坡的地應力場。初始地應力場是在工程設計中需要考慮的重要因素。初始地應力σz是由土體自重應力和河谷地質演化釋荷引起的。由于本研究山體在沒有超載的情況下，初始應力場通常為巖土體的自重應力場。由于巖土體經歷歷史上長期的固結，一般早已達到穩定狀態，所以初始位移通常假設為零。

如果建立一個穩定的模式，能夠不斷復制是最好的。但問題在于，外部的環境和內部的資源是在不斷變化的，模式不可能一勞永逸，當內外部環境發生變化時，企業的生存會遇到挑戰。另外，如果總是簡單的重復，員工的熱情也會喪失。

當采用有限元計算時，一般可采用兩種方法來施加初始地應力。其一是在部分邊界上施加相應的面力荷載，在內部施加自重荷載，通過求解而得到的地應力場作為初始地應力場；其二是將初始應力按自重應力直接輸入高斯點，形成一個初始地應力場。如果沒有條件獲得初始地應力的分布規律，一般可將初始地應力公式取為如下形式：

σz=yz

(2)

σx=σy=Koσx

(3)

τxy=τyz=τzx=0

(4)

式中：σz為初始地應力；z為應力點的深度；K0為土的靜止土壓力系數；γ為土體的重度。計算出相應點處的初應力后，直接送往各個單元的初始應力場函數從而形成初始地應力。

2.3 土體開挖的計算方法

有限元模擬開挖，關鍵是使開挖面上的應力得到解除，成為自由面。因此對于每級開挖要根據開挖前的應力求出剩余土體V2對即將開挖部分土體V1所作用的結點力{F}，在開挖后將{F}反向作用在開挖面結點上，并將挖去土體從結構中去掉，進行下一步的有限元計算。對開挖掉的土體單元，如果從分析對象的結構中去掉，一般有兩種處理方法：

1)保留原來的土體單元網格，采用空單元置換法，將挖掉的土體單元以空單元代替，及降低土單元的彈性模量，使得無論計算多少個開挖步，總剛度矩陣不變。

2)把挖掉的單元從網格中刪掉，使結構中不再包含這些單元。但這種方法需要重新對結構所劃分的網格進行排列、編號，從而使得結構剛度陣、荷載列陣等均需做一系列調整而使實際應用起來較煩瑣。

對于第一種方法，在處理上較為簡單，但當彈性模量降低較多時，會因單元剛度陣太小使總剛度矩陣成為病態矩陣，增加解方程的難度。根據前人計算經驗，當彈性模量降低兩個數量級時，計算結果是可以滿足工程上的精度要求的，而且求解方程組不會出現困難。

對于挖掉的結點，考慮到其對存在的結點已不起任何作用，因此，可令其各方向的位移為0。這樣就不會對現存結點產生影響。在具體的程序操作中，可令被挖掉的結點的位移相對應總剛中的元素為一大數，這樣，解得的位移將等于一極小值，可近似作為0。

3 玻璃橋橋址邊坡穩定性分析

3.1 有限元三維模型的建立

根據地形等高線圖采用三維建模軟件處理，獲得的三維地質模型如下圖4：

圖4 某玻璃橋大峽谷三維實體圖Fig.4 Three-dimensional entity figure of glass bridge canyon

根據勘察單位所提供的地質剖面圖及地形圖(見圖5和圖6)建立適合有限元計算的模型，取最不利的剖面即橋中線所在的剖面進行拉伸形成，建立三維有限元計算模型見圖7和圖8。

圖5 某玻璃橋大峽谷剖面Fig.5 Profile of glass bridge grand canyon

圖6 某大峽谷玻璃橋場平面圖Fig.6 Floor figure of glass bridge grand canyon

圖7 某玻璃橋大峽谷有限元計算幾何模型Fig.7 Finite element computational geometry model of glass bridge grand canyon

圖8 某大峽谷玻璃橋錨墩荷載作用面Fig.8 Anchor pier loading surface of grand canyon glass bridge

模型的網格劃分見圖9。

圖9 模型的網格劃分Fig.9 Mesh of the model

模型邊界條件為：模型左右、前后分別是水平方面位移約束，底面為固定端約束。

3.2 計算參數的確定

由于實際山體結構過于復雜，大量分布有溶洞，很難探明溶洞的分布范圍，可以對巖體的力學參數采用概化處理，擬對灰巖力學參數折減20%。對于傾向峽谷方面的對山體穩定性有控制作用的兩條節理以內的巖體由于其風化作用力學參數折減30%。節理參數擬采用巖溶充填物的參數，計算所采用的力學參數見下表1。

表1 巖石(體)物理性力學參數

巖體、混凝土錨墩均采用SOLID實體單元模擬。模型上邊界為自由邊，其它邊界為位移約束。荷載值按設計施加，自重應力場采用ABAQUS內部特有的應力平衡法將自重應力在施加過程中所引起的初始位移場取消，荷載根據需要可以一次加載也可以根據實際情況分期加載。

計算荷載左右岸錨墩分別作用豎向荷載為1.5×104kN，水平荷載為5×102kN。

3.3 計算結果分析

3.3.1 初始地應力計算

根據上述方法計算出的初始應力場如圖10和圖11所示。

由圖10可見初始應力場最大值出現山谷的左岸溝谷中間部分，約為2.5×102kN。

由圖11可見右岸溝谷內初始應力場最大值出現右岸溝谷中上部，約為2.1×102kN。

圖11 峽谷右岸邊坡的自重應力場分布Fig.11 Slope gravity stress field distribution of canyon right bank

3.3.2 外荷載作用下的有限元模擬

根據設計資料，計算荷載為玻璃橋作用在左右岸錨墩的豎向荷載均為1.5×104kN，水平荷載為5×102kN。錨墩面積為522 m2，故錨墩表面受正壓力為28.7 kPa，剪切布力為9.5 kPa。

圖12 外荷作用下峽谷左岸邊坡的應力場Fig.12 Slope stress field of canyon left bank under the action of load

圖13 外荷作用下大峽谷右岸邊坡的應力場分布Fig.13 Slope stress field of canyon right bank under the action of load

圖14 沿峽谷模型中線從左向右岸的應力分布Fig.14 Stress distribution along the canyon calculation center line from left to right bank

由圖12～圖14可看出某玻璃橋大峽谷所受應力在外荷作用下由坡頂向溝谷深度應力越來越大，在坡谷的中下部達到極大，然后又逐漸變小，均比修橋前僅在自重應力作用下大，處于不穩定狀態。左岸受力情況要比右岸的更不利。

由圖15～圖17可看出某玻璃橋大峽谷在外荷作用下在左岸谷坡的中下部發生塑性破壞，由位移分布圖可以看出破壞區有部分發生向上的位移，表明該破壞主要是沿節理面發生滑移，推動谷底下部巖土體有拱起的趨勢。

圖15 玻璃橋大峽谷在外荷作用下塑性區分布Fig.15 Plastic zone distribution of glass bridge grand canyon under the action of load

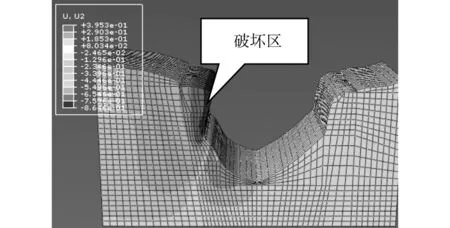
圖16 玻璃橋大峽谷在外荷作用下豎向位移云圖Fig.16 Vertical displacement contours of glass bridge grand canyon under the action of load

圖17 玻璃橋大峽谷在外荷作用下位移失量Fig.17 Displacement vector contours of glass bridge grand canyon under the action of load

由于該大峽谷玻璃橋東西橋墩位置場地(靠近大峽谷附件區域)落水洞、垂直溶蝕裂隙(張裂縫)及溶溝、溶槽發育，尤其是張裂縫的形成說明場地巖體中的破壞已經形成，是場地潛在不穩定的標志。數值分析結果表明，所計算采用的設計橋址位置不宜建設玻璃橋及配套工程。因此，作為西側橋墩位置建議應避開不良地質作用發育的區域。若橋址位置不能移動，則應對不良地質作用發育區域的巖體進行加固治理；作為東側橋墩位置建議宜避開不良地質作用發育的區域。若橋址位置不能移動，則應對不良地質作用發育區域的巖體進行加固治理。

4 結論

1)研究了采用Abaqus軟件解決巖土工程問題，本構模型的選擇及模型應用所注意的問題。

2)建立了某大峽谷三維有限元模型，計算了大峽谷初應力場的分布，并在設計荷載作用下玻璃橋橋址邊坡的附加應力、位移場及破壞區的分布規律。

3)根據數值模擬分析結果，所計算橋址的位置在外力作用下處于欠穩定-不穩定狀態，如不采取加固措施，不適宜建設玻璃橋，建議改變橋址設計位置或對不良地質作用發育區域的巖體進行加固治理。

[1] 郭子儀, 范振華. 邊坡穩定性分析中的有限元極限平衡法[J]. 武漢理工大學學報, 2014, 1(38): 79-84. GUO Ziyi, FAN Zhenhua. Finite element limit equilibrium method for slope stability analysis [J].Journal of Wuhan University of Technology, 2014, 1(38): 79-84.

[2] Liu Y Q, Li H B, Dai H C. Preliminary study on the progressive failure of a layered rock slope under explosions [J]. Key Engineering Materials, 2006, 36(8): 1461-1466.

[3] Kim J, Salgado R, Lee J. Stability analysis of complex soil slopes using limit analysis [J]. Journal of Engineering, ASCE, 2002, 128(7): 546-557.

[4] Manzari M T, Nour M A. Significance of soil dilatancy in slope stability analysis [J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2000, 126(1): 75-80.[5] 沈華章, 郭明偉. 基于離散元的邊坡矢量和穩定性分析方法研究[J]. 巖土力學, 2016, 37(2): 592-600. SHEN Huazhang, GUO Mingwei. Vector sum method for slope stability analysis based on discrete elements [J]. Rock and Soil Mechanics, 2016, 37(2): 592-600.

[6] Stianson J R, Fredlund D G, Chan D. Three—dimensional slope stability based on stresses from a stress—deformation analysis [J]. Canadian Geotechnical Journal, 2011, 48(6): 891-904.

[7] 孟慶文, 冷伍明. 山區高速鐵路高陡邊坡穩定性與變形分析[J]. 鐵道科學與工程學報, 2012, 9(6): 55-59. MENG Qinwen, LENG Wuming. Research of stability and deformation on the high and steep slope of high speed railway in mountainous regions [J]. Journal of Railway Science and Engineering, 2012, 9(6): 55-59.

[8] 張利國, 王春雷. 客運專線橋基高邊坡穩定性三維有限元分析[J]. 鐵道工程學報, 2010, 2(2): 45-58. ZHANG LiGuo,WANG ChunLei. Three-dimensional finite element analysis of stability of high-steep slope under load of bridge of passenger dedicated line [J].Journal of Railway Engineering Society, 2010,2(2): 45-58.

[9] 彭富強, 袁昕. 婁新高速復雜地質邊坡治理研究及穩定性分析[J]. 鐵道科學與工程學報, 2013, 10(4): 106-111. PENG Fuqiang, YUAN Xin. Research on management and stability analysis of Lou-Xin high speed complex geological slope [J]. Journal of Railway Science and Engineering, 2013, 10(4): 106-111.

[10] 盧應發, 黃學斌. 推移式滑坡漸進破壞機制及穩定性分析[J]. 巖石力學與工程學報, 2016, 35(2): 334-345. LU Yingfa, HUANG Xuebin. Mechanism and stability analyses of progressive failure of thrust-type landslides [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(2): 334-345.

[11] 曹杰峰, 曹金鳳.考慮初始地應力的海底斜坡穩定性分析[J]. 青島理工大學學報, 2014, 35(3): 19-22. CAO Jiefeng, CAO Jinfeng. Study on the stability of submarine slopes considering the initial geosttress field [J]. Journal of Qingdao Technological University, 2014, 35(3): 19-22.

The stability analysis of the slope of glass bridge site in a grand canyon

JIN Shubin1, HU Tao1, QIAO Shifan2

(1.Guizhou Highway Engineering Group Co., Ltd, Guiyang 550008, China；2. School of Civil Engineering, Central South University, Changsha 410075, China)

Based on the finite element method, the stability analysis of the steep slopes with anchor bars at both sides of a grand canyon was conducted and the originally designed bridge site was evaluated for the construction and operation safety of the glass bridge. The plastic zone distribution regulation of the slope under the condition of glass bridge loading was obtained by simulating the displacement and stress states of the slope under natural and bridge loading conditions. Three dimensional finite element software was used in combination with the geotechnical engineering conditions for this purpose. The results show that the position of bridge site was between metastable state and unstable state under the action of external forces. It is suggested to change the design position of bridge site or reinforce rock mass in regions susceptible to disastrous geological development. This offers reference for the further design of a canyon glass bridge.

slope stability analysis; three dimensional finite element; displacement state; stress state; numerical simulation

2016-02-25

貴州省交通廳科技資助項目(2015-122-047)

喬世范(1975-)，男，山東莒南人，教授，從事環境巖土工程及巖土信息三維可視化仿真技術等方面的教學和科研工作；E-mail:qiaoshifan@163.com

TU47

A

1672-7029(2016)11-2197-07