基于模型試驗的曲線部分斜拉橋施工過程模擬分析

彭晶蓉，賀拴海，王凌波

(長安大學 公路學院，陜西 西安 710064)

?

基于模型試驗的曲線部分斜拉橋施工過程模擬分析

彭晶蓉，賀拴海，王凌波

(長安大學 公路學院，陜西 西安 710064)

為研究曲線部分斜拉橋采用對稱懸臂施工方法施工的結構受力特點，根據相似理論，對依托工程制作了1/40的全橋縮尺模型。通過模型試驗模擬施工過程中主梁澆筑、斜拉索張拉、主梁合龍、橋面鋪裝等關鍵工序，并測試主梁截面應力及變形、斜拉索索力等關鍵斷面隨施工過程發展的變化規律。結果表明，有索區梁段在施工過程中頂、底板均呈拉壓交替變化，實橋設計中應著重關注；模型橋的懸臂施工對稱點的測試數據基本一致，表明該模型對稱性較好；模型理論計算值與試驗實測值規律吻合，驗證了結構計算理論，且實測值均偏安全，表明模型結構剛度較大、安全性較高；理論模型與模型試驗相結合對研究復雜結構的受力具有可行性。

部分斜拉橋；模型試驗；懸臂施工；施工過程

橋梁結構力學性能和受力特點的研究方法通常假以模型試驗與理論計算相結合的方式進行。模型試驗是對原型橋按原尺寸或一定的比例尺進行縮小，在模型上施加荷載來分析結構的性能，再以相應的比例關系換算到原型橋上，對原型橋的性能進行分析[1-5]。因此，橋梁模型具有經濟性好、影響因素更為可控、針對性強、周期較短、拆卸方便等優點[6-8]。國內結構模型試驗為數不少，張在銘[9]在某斜拉橋有機玻璃模型試驗中，按1/40進行縮尺，塔梁采用有機玻璃，斜拉索采用高強鋼絲，對成橋階段的受力狀況進行試驗驗證，分析了該類新橋型的整體受力性能；高小妮[10]在三塔斜拉-自錨式懸索組合體系橋中按1/20制作全橋縮尺模型，研究了該體系在成橋階段對稱與非對稱荷載作用下加勁梁、吊桿、拉索、主塔與副塔的力學行為等。參考資料顯示，目前對部分斜拉橋的模型試驗鮮見，尤其模擬結構施工過程的研究未見報道。本文通過對部分斜拉橋的懸臂施工過程進行模擬，研究關鍵控制斷面在各個階段的受力特點，以檢驗該結構整個施工過程的安全性與合理性，并結合試驗結果對結構計算理論進行驗證，以對實橋的設計施工提供參考。

1 模型試驗設計

1.1 模型參數

依托工程為曲線部分斜拉橋(108+208+108) m，平面位于曲線R=1 800 m上；主梁采用預應力混凝土箱梁結構，梁從塔根部到跨中截面高度由6 m變至3.6 m，半幅橋寬20.5 m，主橋為墩、塔、梁固結體系，邊墩處設置支座，橋型布置如圖1。

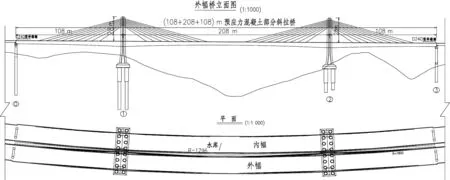
單位：m圖1 某曲線部分斜拉橋總體布置圖Fig.1 General layout of a curved Extra-dosed bridge

本模型試驗的縮尺比取為1/40，主梁采用鋁合金板材，主塔采用Q235B碳素鋼板，斜拉索采用直徑2.5 mm的高強鋼絲，塔梁處先螺栓錨固后焊接以模擬固結方式。邊座支采用鋼架模擬豎向、橫向及縱向的約束。根據相似理論進行換算，縮尺后變截面梁從塔根部到跨中截面高度由15 cm變至9 cm；腹板、頂板及底板模型板厚分段采用與原橋對應節段平均板厚縮尺尺寸，由于混凝土結構中的預應力效應無法換算至模型結構中，因此不與實橋效應值直接對比分析。

1.2 施工階段劃分

橋梁模型的主要施工階段可分為墩塔施工、主梁懸臂施工及拉索張拉、合龍段施工及二期鋪裝。模型各節段主梁按施工順序分節段焊接，以0號塊為中心對稱，邊、中跨方向各分7個對稱主梁節段，8號節段為邊跨合龍段，8’號節段為中跨合龍段，焊接每個節段后施加對應節段的自重補償荷載、張拉該節段拉索(無索區無需張拉)。整個模型建造過程主要階段及對應有限元分析模型如圖2所示。由于全橋結構對稱，模型示意及數據分析僅以1號墩為例。

在模擬施工過程中配重是補償混凝土和鋁合金的材性差異的關鍵因素[11-12]，根據表1中均布荷載的相似關系對各施工節段進行自重補償模擬，配重均在梁底采用吊籃進行加載，具體加載位置及荷載值如圖3與表1所示。

(a)無索最大懸臂階段；(b)拉索懸臂階段；(c)最大懸臂階段；(d)邊跨合龍階段；(e)中跨合龍階段圖2 模型主要建造過程及對應有限元分析模型Fig.2 Main construction process and corresponding finite element analysis model

單位：cm圖3 1號墩模型設計示意圖Fig.3 Model design diagram of 1# pylon

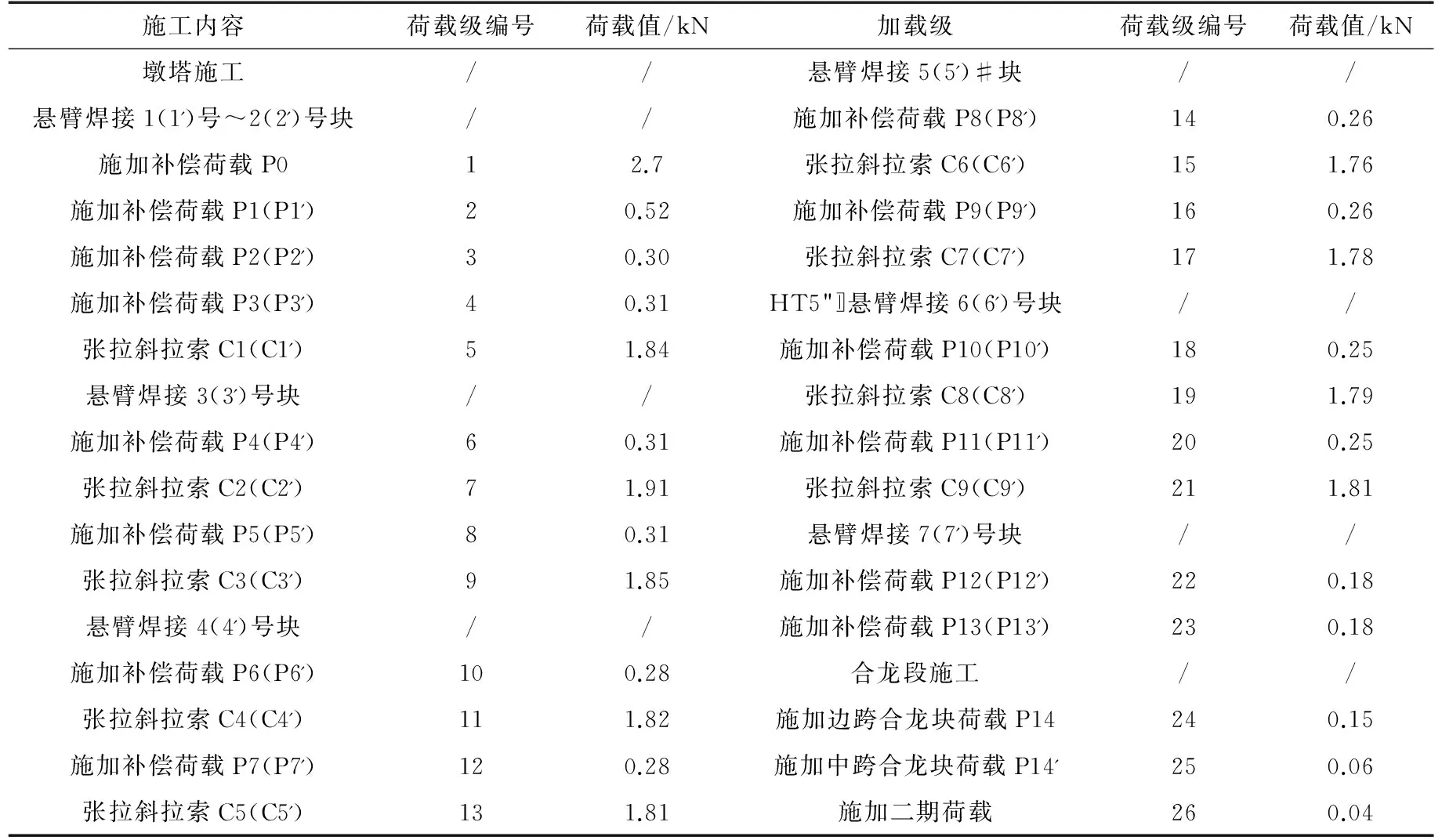
施工內容荷載級編號荷載值/kN加載級荷載級編號荷載值/kN墩塔施工//懸臂焊接5(5')#塊//懸臂焊接1(1')號～2(2')號塊//施加補償荷載P8(P8')140.26施加補償荷載P012.7張拉斜拉索C6(C6')151.76施加補償荷載P1(P1')20.52施加補償荷載P9(P9')160.26施加補償荷載P2(P2')30.30張拉斜拉索C7(C7')171.78施加補償荷載P3(P3')40.31HT5"?懸臂焊接6(6')號塊//張拉斜拉索C1(C1')51.84施加補償荷載P10(P10')180.25懸臂焊接3(3')號塊//張拉斜拉索C8(C8')191.79施加補償荷載P4(P4')60.31施加補償荷載P11(P11')200.25張拉斜拉索C2(C2')71.91張拉斜拉索C9(C9')211.81施加補償荷載P5(P5')80.31懸臂焊接7(7')號塊//張拉斜拉索C3(C3')91.85施加補償荷載P12(P12')220.18懸臂焊接4(4')號塊//施加補償荷載P13(P13')230.18施加補償荷載P6(P6')100.28合龍段施工//張拉斜拉索C4(C4')111.82施加邊跨合龍塊荷載P14240.15施加補償荷載P7(P7')120.28施加中跨合龍塊荷載P14'250.06張拉斜拉索C5(C5')131.81施加二期荷載260.04

1.3 測點布置與測試方法

1)應變測點布置

施工過程中1號墩主梁測試邊跨1/3、2/3斷面，墩頂兩側主梁截面，中跨1/8、2/8及中跨跨中共7個關鍵斷面的應變值。主梁應變測試截面的測點布置如圖4所示，頂板及底板分別等間距布置5個測點。

圖4 主梁截面應變測點布置圖Fig.4 Strain monitoring points of girder

2)撓度測點布置

撓度測試點主要關注施工過程中測試斷面的變位狀態及線形變化，1號墩塔主梁撓度測試截面測點分別是邊跨1/4、2/4、3/4點處，0#塊處，中跨的1/6、2/6及跨中處共7個，每個截面2個測點，如圖5所示。

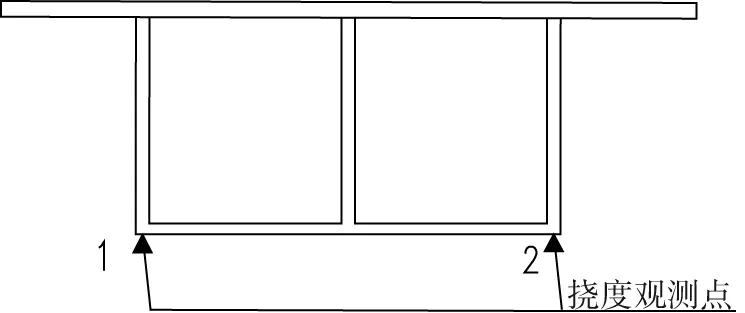
圖5 主梁撓度測點布置示意圖Fig.5 Displacement monitoring points of girder

3)索力測點布置

全橋144根拉索張拉端均布置S型拉力傳感器或鋼筋計。本試驗中針對2.5 mm直徑的斜拉索，專門設計了錨固裝置來控制調節拉索初張拉力并監控施工過程中斜拉索索力變化。

2 主梁施工階段模擬試驗分析

模型模擬實橋由墩塔到主梁懸臂施工至合龍全過程，并將試驗實測值與模型橋有限元計算值進行對比分析，由于篇幅有限，本文分析部分測試斷面應變、撓度和索力數據隨施工過程的變化規律，與模型計算值進行比較。

2.1 應變分析

各截面應變測試點布置如圖5所示，選取墩頂處主梁C-C截面與中跨跨中G-G截面的頂底板中點即2，7，12和17號測試點，分析施工過程中各荷載級下測點應力的變化規律分別如圖6～圖9所示。

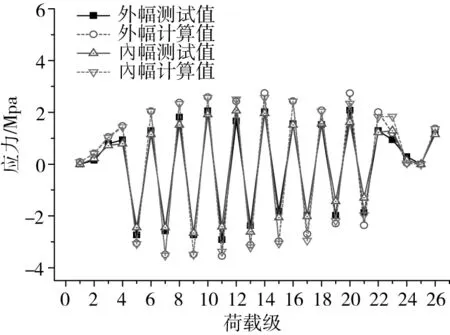
圖6 C-C截面外幅頂板應變變化圖Fig.6 Strain variation diagram of C-C top flange Fig

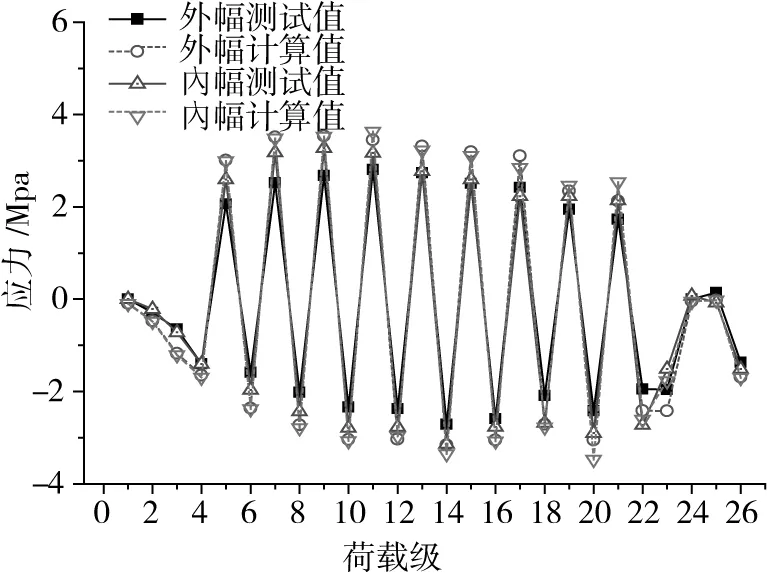
圖7 C-C截面外幅底板應變變化圖Fig.7 Strain variation diagram of C-C bottom slab

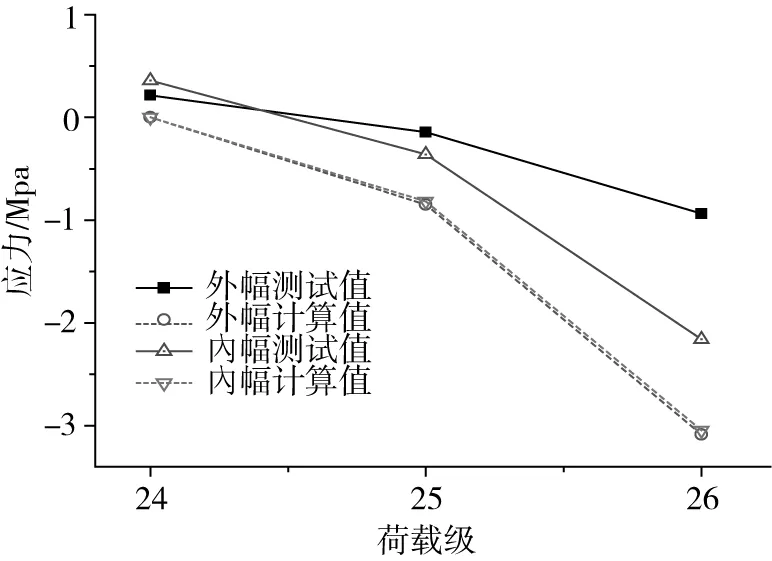
圖8 G-G截面內幅頂板應變圖Fig.8 Strain variation diagram of G-G top flange

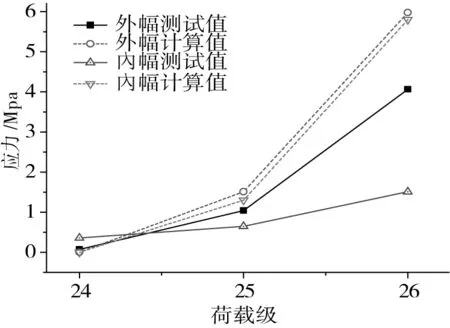
圖9 G-G截面內幅底板應變圖Fig.9 Strain variation diagram of G-G bottom slab

由圖6～圖9可知，C-C截面的頂板在第1～4荷載級作用下，拉應力呈增大趨勢，張拉C1索后，頂板呈受壓狀態；且伴隨懸臂施工過程，配重荷載和斜拉索張拉交替進行，則頂板應力呈拉壓交替變化，合龍節段及二期荷載對應力變化范圍明顯小于拉索張拉。底板應力拉壓狀態與頂板相反。G-G截面為中跨跨中截面，合龍段自重與二期荷載均使得該截面頂板受壓，底板受拉。各截面應力值測試值與計算值變化趨勢一致，各測點實測值均小于計算值，故可認為模型設計安全。

2.2 撓度分析

主梁撓度選取2-2與6-6截面進行分析，撓度在各加載級下的相對變化值與相應的累加值如圖10～圖13所示，其中負值表示主梁下撓。

圖10與圖12為測試截面各荷載級級單次加載的測點變形規律，同一測試點主梁外幅變形值略大于內幅，測試值亦然。在主梁有索區懸臂施工過程中，配重荷載和斜拉索張拉交替進行，測點撓度值也呈現下撓、上拱交替變化的規律，合龍階段即24、25加載級引起的撓度變化值較小，而二期荷載使得主梁下撓。

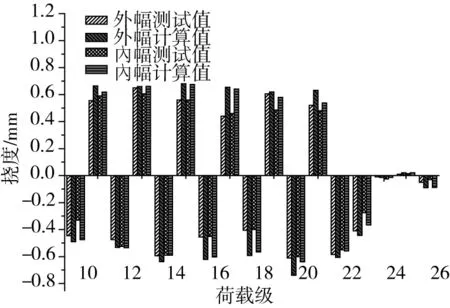
圖10 2-2截面各加載級撓度變化圖Fig.10 Deflection diagram under different loading of 2-2 section

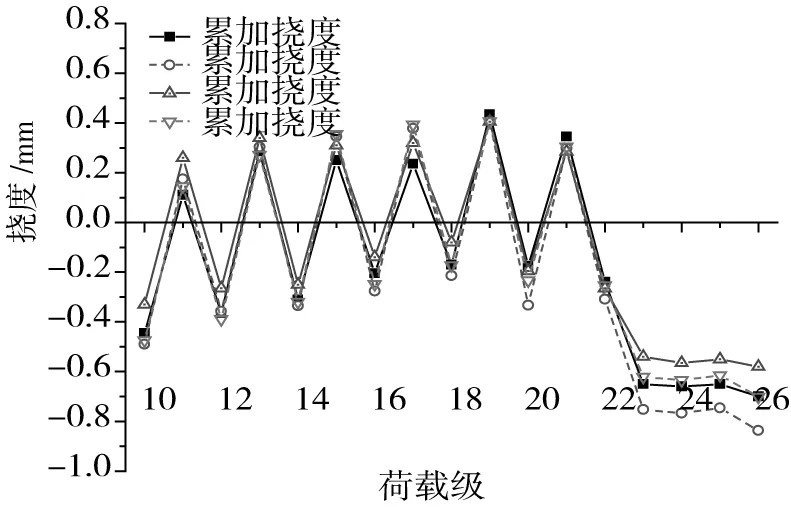
圖11 2-2截面撓度累加變化圖Fig.11 Cumulative variation deflection of 2-2 section

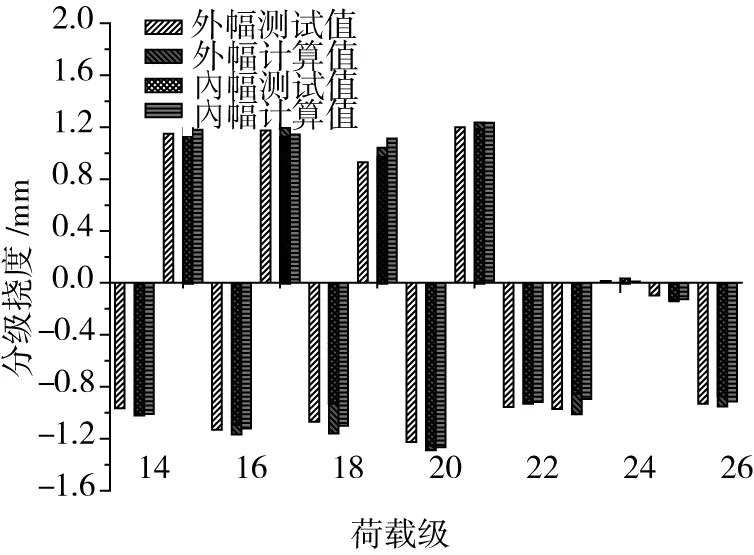
圖12 6-6截面各加載級撓度變化圖Fig.12 Deflection diagram under different loading of 6-6 section

圖13 6-6截面撓度累加變化圖Fig.13 Cumulative variation deflection of 6-6 section

圖11與圖13為測試截面變形的絕對值，測試值與計算值變化規律一致，隨著施工過程的進行，實測值與理論計算值的差值并無累加趨勢，如6-6截面外幅主梁在各荷載級下的最大撓度差為0.12 mm，而累加值成橋誤差僅為0.09 mm。經有限元計算分析及試驗測試可知，主梁最大撓度為中跨跨中(6-6截面)處。因此，將合攏段作為撓度控制截面，合攏段外幅撓度為-2.87 mm，內幅撓度為-2.61 mm，模型橋計算值分別為-2.92 mm與-2.66 mm，試驗值較理論計算值小。分析表明，模型中主梁剛度較大，對成橋后活荷載作用下結構安全性有利。

2.3 索力分析

該曲線部分斜拉橋為“III”塔四索面，斜拉索索力變化值分析選取1號墩邊跨C1索和對應中跨側C1’索的施工過程索力變化值與最外側索面的成橋索力進行分析，其變化規律如圖14～圖17所示。

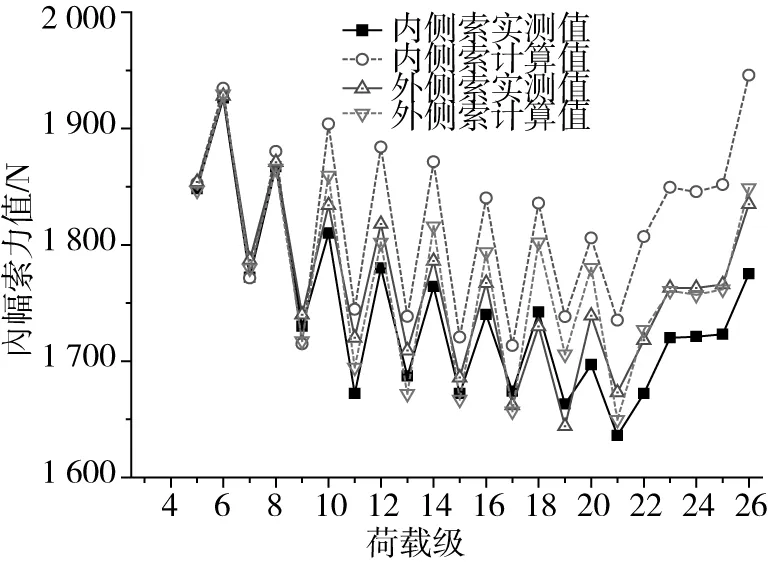
圖14 1號塔邊跨外幅C1索力變化圖Fig.14 Cable force variation diagram of outside C1 in side-span of 1#pylon

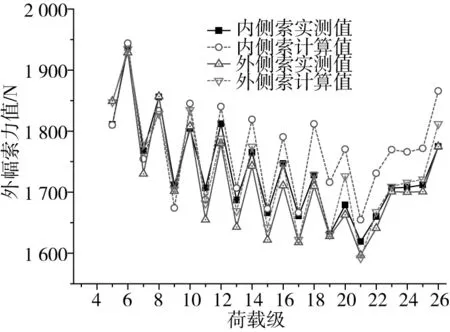
圖15 1號塔邊跨內幅C1索力變化圖Fig.15 Cable force variation diagram of inside C1 in side-span of 1#pylon

有索區實驗過程中，每個加載級均會對已施工拉索的索力值進行測試，由于施工步驟中主梁自重補償與拉索張拉穿插進行，索力基本呈波浪變化。由圖14～17可知，主梁內、外側索面的索力不同，內側索力均略大于外側索力，合龍段施工對索力影響可忽略不計；24荷載級之前C1索與C1’索完全對稱，故索力變化一致，但二期荷載(第26荷載級)使得索力增大，且中跨側索力增加幅度較大。

圖16 1號塔中跨外幅C1’索力變化圖Fig.16 Cable force variation diagram of outside C1 in mid-span of 1#pylon

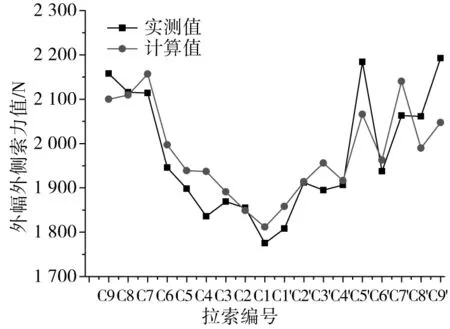
圖17 1號塔外幅索面成橋索力值Fig.17 Cable force variation diagram of inside C1 in mid-span of 1#pylon

由斜拉索受力行為分析可知，部分斜拉橋在計算中斜拉索采用Ernst公式修正后的桁架單元計算值與試驗結果較吻合，模型結構兩側試驗值接近，說明該模型制作對稱性較好，模型設計所用的計算原理與計算軟件能較準確地模擬部分斜拉橋的受力特征。

3 結論

1)根據相似理論確定模型參數、選材、確定荷載補償及加載方式等模擬了原型橋的施工過程受力情況，通過理論計算與測試結果的對比發現，該方法對研究復雜結構的受力具有可行性。

2)部分斜拉橋模型計算中采用梁單元模擬，斜拉索采用Ernst公式修正后的桁架單元模擬能較好的地反映結構的受力特點，也能準確反映索力變化規律。

3)模型橋的對稱懸臂施工對稱性好，剛度較大，結構施工過程及后期運營過程結構安全度較高。模型在相似理論的基礎上進行加工，并模擬實橋的施工工藝進行；

4)本次模型試驗針對2.5 mm斜拉索的錨固與索力調節裝置進行了特殊設計，通過測試結果與理論計算值對比可知，該設計有效且精度滿足試驗要求，可為同類型試驗提供參考。

[1] 趙煜,張鋒,周勇軍，等.多跨斜拉-自錨式懸索組合體系橋全橋靜力模型試驗[J].長安大學學報(自然科學版),2012,32(5):45-51,64. ZHAO Yu, ZHANG Feng, ZHOU Yongjun, et al. Static model test of multi-span cable-stayed and self-anchored suspension composite bridge[J]. Journal of Chang’an University. 2012, 32(5):45-51,64.

[2] Llanos,Fernando Flórez,Aguilar,et al.New bridge over the danube: vidin-calafat[J]. Journal of the International Association for Bridge and Structural Engineering, 2014, 24(3): 414-419.

[3] 葉梅新,李恩良,侯文琦.單索面斜拉橋主梁變寬段模型試驗方法[J].中南大學學報(自然科學版),2011,42(1):199-206. YE Meixin, LI Enliang, HOU Wenqi. Test method on mutative width girder segment of single plane cable-stayed bridge[J].Journal of Central South University (Science and Technology) ,2011,42(1):199-206.

[4] KOU Changhuan,WU Tsungta.Optimization of cable force of extra-dosed bridges[J]. Applied Mechanics and Materials, 2014(587-589):1577-1580.

[5] Stroh S L. Proportioning and design considerations for extra-dosed prestressed bridges [C].//Sustainable Bridge Structures - 8th New York City Bridge Conferences. NewYork, NY, United states: CRC Press/Balkema, 2015:157-170.

[6] Collings, David, Gonzalez,et al. Extra-dosed and cable-stayed bridges, exploring the boundaries [J].2013:166(4): 231-239.

[7] 肖明葵，王肖巍，劉綱.多塔下拉索斜拉橋靜力荷載試驗和計算分析[J].土木建筑與環境工程,2011,33(1):43-49. XIAO Mingkui, WANG Xiaowei, LIU Gang. Static load test and calculation on multi-tower cable-stayed bridge with tie-down cables[J]. Journal of Civil, Architectural& Environmental Engineering,2011,33(1):43-49.

[8] 肖凱.基于剛度相似原理的斜拉橋縮尺模型的設計研究[D].武漢:武漢理工大學,2012. XEAO Kai. Research on design of cable-stayed bridge’s scale model based on stiffness similarity theory.[D].Wuhan: Wuhan University of Technology,2012.

[9] 張在銘.部分斜拉橋有機玻璃模型試驗綜述[J].福建建設科技,2006(3):28-29. ZHANG Zaiming. Review of the experimental model of extra-dosed bridges with organic glass[J]. Fujian Construction Science and Technology. 2006(3):28-29.

[10] 高小妮，賀拴海，趙煜，等.三塔斜拉-自錨式懸索組合體系橋成橋階段活載模型試驗研究[J].武漢理工大學學報,2012,34(1):84-89. GAO Xiaoni, HE Shuanhai, ZHAO Yu, et al. Model test on cable-stayed and self-anchored suspension combination bridge with three towers under live loading in finished stage[J]. Journal of Wuhan University of Technology, 2012,34(1):84-89.

[11] 李忠獻．工程結構試驗理論與技術[M]．天津：天津大學出版社，2004． LI Zhongxian. theory and technology of engineering structure test[M].Tianjin:Tianjin University Press,2004.

[12] 章關永．橋梁結構試驗[M]．北京：人民交通出版社，2002． ZHANG Guanyong. Bridge structure test[M]. Beijing: China Communication Press,2002.

Simulation and analysis of the curved extra-dosed bridge construction based on model test

PENG Jingrong，HE Shuanhai，WANG Linbo

(School of Highway, Chang’an University, Xi’an 710064, China)

In order to study the structure of the curved extra-dosed bridge with cantilever construction method, a full bridge model was made with the ratio 1/40 to the in-situ bridge based on the similarity theory. The variations of the stress and deformation of girder and cable force under different construction loads such as main girder casting, cable tension, closure, deck pavement in different construction process were measured. The results show that the stress of top deck and bottom slab of girder in cable anchored area are in alternating tension-compression cycles which should be laid emphasis on in practical designing. The calculated values of the model are in good agreement with the experimental ones, which verifies the calculation theory. The cantilever construction of the model bridge is symmetrical, with high rigidity and high safety. It is feasible to combine the theoretical model and the model test for the research of the complex structure.

extra-dosed bridge; model test; cantilever construction; construction process

2016-03-15

廣東省交通運輸廳科技資助項目(科技-2014-02-017)

賀拴海(1962-)，男，陜西洛川人，教授，博士，從事橋梁結構理論研究；E-mail:hshai@chd.edu.cn

U44

A

1672-7029(2016)11-2189-08