孔內抽水引起的樁周地表沉降計算方法研究

劉金海，吳霞，王娟

（1.贛州中科工程管理有限公司，江西贛州 341000；2.江西應用技術職業學院，江西贛州 341000；3.陜西鐵路工程職業技術學院，陜西渭南 714000）

孔內抽水引起的樁周地表沉降計算方法研究

劉金海1，吳霞2，王娟3

（1.贛州中科工程管理有限公司，江西贛州 341000；2.江西應用技術職業學院，江西贛州 341000；3.陜西鐵路工程職業技術學院，陜西渭南 714000）

針對富水地區樁基工程施工中樁孔內滲水量較大的特點，考慮樁基孔內抽水導致水位下降而引起樁周地表沉降，分析一種潛水完整井穩定滲流下的樁周地表沉降計算方法。根據滲流理論分析推導了降水滲流下樁基周圍土體單元的有效應力增量；采用二維平面范圍內進行二重積分計算的方法，分析了滲流作用下孔內降水引起的樁周地表沉降計算公式。以具體工程為依托，分別采用現場實測與公式計算的方法對樁周地表沉降進行預測，結果表明實測值與計算值整體上較為接近，但在距離樁孔邊緣3 m范圍內，實測值大于計算值，而5 m范圍外的計算值與實測值較為接近，同時沉降值隨著與樁孔邊緣距離的增大而減小。

橋梁；樁基礎；樁周沉降；滲流；富水地區

在地下水位較豐富的地區，樁基在成孔掘進過程中易受到地下水的影響。樁孔的開挖掘進為孔周土體的側向移動提供了臨空面，并為地下水的滲流提供了新路徑。與大型基坑開挖相比，樁基孔成孔中樁孔開挖面范圍較小，相關研究與大量工程實際表明，由于土體開挖而引起的樁孔周圍土體的側向位移和豎向沉降較小，在實際分析計算時應主要考慮由于地下水的降水滲流所引起的沉降。

樁基孔內抽水導致地下水位下降，一方面使孔隙水壓力得以消散而轉移為有效應力，樁周土體單元的自重有效應力增大，土顆粒的接觸更緊密。另一方面，孔內降水導致孔內外存在水頭差，根據滲流理論，在水頭差作用下降水豎向滲流會給土顆粒施加單位體積上的動水壓力，使土顆粒產生附加沉降。自重有效應力的增加和豎向動水壓力都會導致土顆粒更加密實而固結，在豎向表現為沉降。顯然，土體的沉降與土單元的應力變化有直接聯系，而樁孔內抽水勢必引起地下水位下降，進而引起樁孔周圍土體應力發生變化。該文根據滲流理論和固結理論，分析樁基孔周土體在孔內抽水條件下的地表沉降，推導其沉降計算公式。

1 降水對孔周土有效應力的影響

孔內抽水會導致孔周土體中的地下水位下降，土體單元的自重有效應力和滲流有效應力增長（見圖1）。假設沿地表水平方向為X方向，沿土體深度方向為Y方向；在土體h深度處取任意一土體單元，該單元在X、Y、Z 方向的長度分別為d X、d Y、1；原始地下水位深度為h0，孔深為H；地下水位以下的土體處于飽水狀態，h0深度范圍內土體的重度為γ0，地下水位以下土體的重度為γ′，孔隙水壓力為σw，降水為潛水完整井穩定流。在開挖掘進中，不考慮施工動載對樁孔周圍土體初始應力的影響。

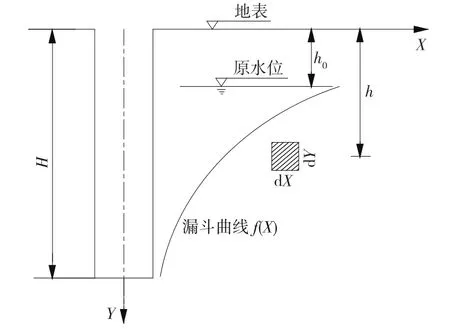
圖1 降水漏斗示意圖

1.1 自重有效應力變化

在地下水位未下降前，對于水位以下的土體單元，其應力由土顆粒和孔隙水壓力共同承擔；在水位下降后，孔隙水壓力得以消散，土顆粒失去上浮力，在自重作用下所承擔的接觸應力將增大，通過土顆粒接觸產生的有效應力得以增長。

水位下降前，水下h深度處土體單元的有效應力σ′=σ-σw，其中總應力σ=h0γ0+（h-h0）γ′，孔

隙水壓力σw=（h-h0）γw。因此，水位下降前土體單元的自重有效應力為：

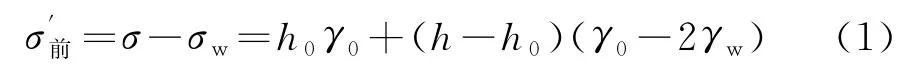
在水位下降超過h深度后，h深度處土體單元的應力僅有自重應力，該土體單元的有效應力為：

水位下降前后h深度處土體單元的有效應力增量為：

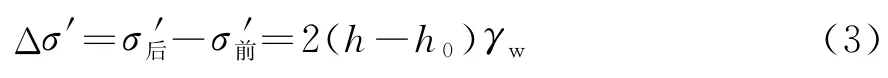
式（3）中的變量均為已知，將其數值代入便可求出水下任意深度處土體單元的有效應力增量。

1.2 滲流有效應力變化

孔內抽水引起水頭差，并為地下水的滲流提供了新路徑。根據滲流理論，地下水在水頭差作用下產生滲流時將給土顆粒施加體積上的動水壓力，當這種動水壓力的方向向下時，土顆粒將在水壓作用下產生下沉而變得更加密實。

土顆粒的下沉產生豎向沉降，而土顆粒的下沉值顯然與動水壓力的大小有關。在動水壓力值的求取方面，苑蓮菊等認為作用在一個單位體積土體單元上的動水壓力值與水力坡降i有關，其表達式為：

動水壓力Dw賦予了土顆粒附加的滲流有效應力。為了求取滲流有效應力，假定滲流僅發生在豎向，此時滲流有效應力可通過計算作用在體積V土體上的動水力與過水面積A的比值來求取，即：式中：體積V等于面積A乘豎向過水路徑h過。

式中：f（X）表示漏斗曲線函數，變量為水平X方向的距離。

將式（4）、式（6）代入式（5），得滲流有效應力：

2 地表沉降計算分析

2.1 地表總沉降分析

樁基孔內抽水，孔周土體地下水水位將下降，土體單元的自重有效應力與滲流有效應力均產生變化增量。自重有效應力與滲流有效應力的作用方向均向下，有效應力增量對土體單元將產生向下的壓縮。錢家歡等認為土體單元在應力增量作用下所產生的微小豎向壓縮可用下式表示：

式中：d s為豎向微小壓縮；Δp為應力增量；e0為土的初始孔隙比；a為壓密系數。

將有效應力增量和滲流應力增量分別代入式（8），得到兩種有效應力下所產生的微小壓縮，分別記為d s1和d s2，其表達式為：

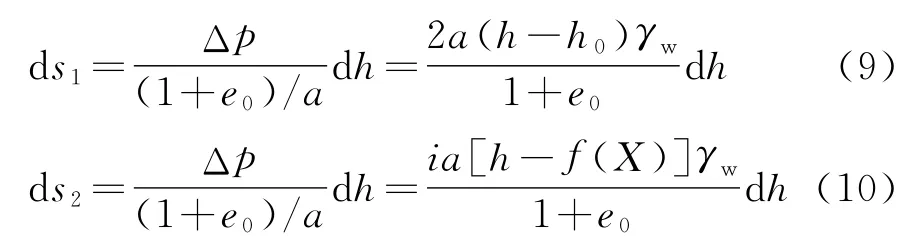
自重有效應力和滲流有效應力均會導致土體產生豎向微小壓縮，故由于降水滲流而產生的土體豎向微小壓縮量d s=d s1+d s2。

假設樁孔周圍土體中的土顆粒在豎向是相互連續接觸的，則當單元土體產生豎向壓縮時，該單元體上部的單元體將同時向下移動，并依次相互影響而最終傳播至地表。根據隨機介質理論，土體中微小豎向壓縮的累加將在地表產生一微小單元凹面，該凹面中心的豎向沉降值Wd按下式計算：

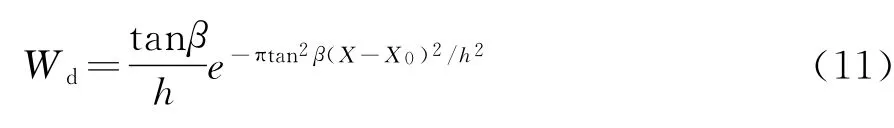
式中：β為樁孔所在地層的影響范圍角，一般可根據前期地質勘察資料獲得；X0為單元體水平方向的邊緣中心點至樁孔邊緣的距離（m）。

顯然，若能對該降水漏斗范圍內的全體微小單元凹面在X和Y軸構成的區域進行二維重積分計算（僅以二維平面計算），便可計算出降水漏斗范圍內的地表沉降，即地表沉降可表示為：

2.2 沉降分類計算分析

樁孔周圍在降水滲流過程中，土體沉降由兩部分貢獻而成：一部分是自重有效應力增量；另一部分是滲流有效應力增量。樁周土體的漏斗曲線隨著降水的不斷進行而產生變化，漏斗曲線以上部分的土體將變為疏干狀態，以下部分的土體則處于滲流狀態。因此，在原水位線至漏斗曲線之間的這部分土體的沉降是由自重應力增量引起的，接觸應力增大，土顆粒變得更加密實；而漏斗曲線以下至孔內水位頂面之間的這部分土體的沉降是由滲流動水壓力引起的（見圖2）。在計算地表沉降時，應以漏斗曲線為分界線，將樁周土體劃分為兩大區域進行二維重積分運算。

圖2 沉降計算示意圖

對于原水位線至漏斗曲線之間的這部分土體，其積分區間，X方向為0～R，Y方向為h0～f（X），則此時沉降值的計算式為：

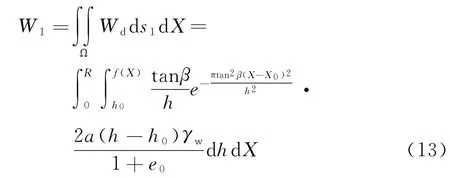
對于漏斗曲線以下至孔內水位頂面之間的這部分土體，其積分區間，X方向為0～R，Y方向為f（X）～（H-h0），則此時沉降值的計算式為：

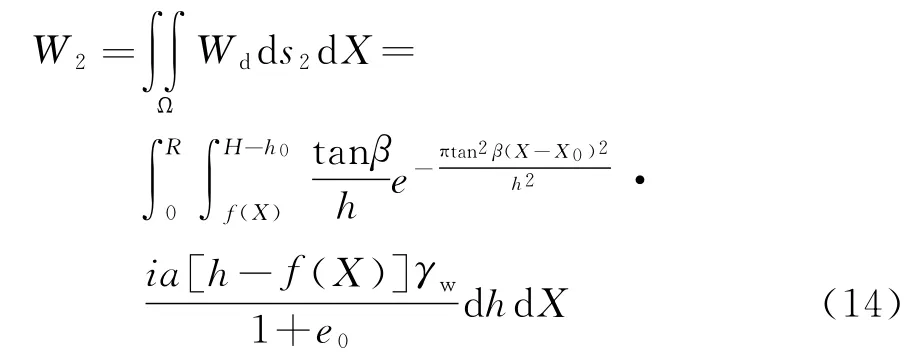
地表總沉降為：

地表總沉降計算的關鍵在于確定漏斗曲線的變化方程f（X）。根據裘布依公式和流量相等性（即相同時間內通過距樁孔軸線不同距離的過水斷面的水流量相等），燕建龍等計算了穩定潛水完整滲流下的漏斗曲線方程，其表達式為：

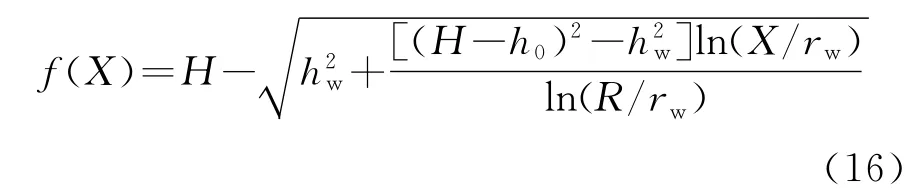
將式（16）代入式（15），即可得到地表沉降值。

3 工程實例

以廣西河池市某樁基工程為依托，采用上述計算公式對孔內抽水條件下的地表沉降進行計算。

該樁孔場地位于農田內，開挖深度為12 m，其地下水以上層滯水和潛水為主。廣西河池地區雨水豐富，屬于巖溶地區，地下水豐富，其上層滯水易受大氣降水影響。實際開挖中，孔內涌水量較大，為保障孔體的穩定，進行孔內抽水減壓處理。地層的主要參數如下：壓密系數a=0.36；初始孔隙比e0= 0.68；地層影響范圍角的正切值為1.12；水力坡降的影響范圍半徑為108 m，水力坡降i=0.06。

同時對地表沉降值進行監測驗證計算結果的有效性。為了防止地表沉降對觀測基準點造成影響，實際監測時將基準點布置在穩定的基巖上，設置3個觀測基準點，以便通過聯測驗證觀測的穩定性。觀測點從樁孔邊緣開始設置，每隔2 m設置一個并逐漸遠離樁孔，共設置11個觀測點。理論上第一個觀測點應設置在樁孔的邊緣，但該設置方式有礙于實際施工作業，故將第一個觀測點設置在距離樁孔邊緣1 m的地方。

圖3為計算結果與實測結果比較。從中可看出：實測值與計算值整體上較為接近，但在距離樁孔邊緣3 m范圍內，計算值與實測值差異較大，實測值大于計算值；而5 m范圍外計算值與實測值較為接近，同時沉降值隨著與樁孔邊緣距離的增大而減小。圖4為由于孔內抽水而導致的農田地表開裂。

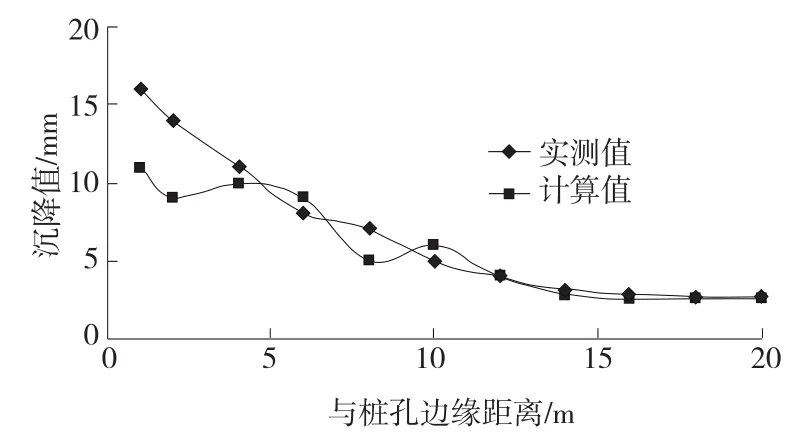
圖3 地表沉降實測與計算結果對比

圖4 樁孔內抽水導致的地表開裂

在距離樁孔邊緣3 m范圍內，實測值大于計算值，這是由孔內抽水導致孔周近距離范圍內土體中的土顆粒流失所致，而該文的計算分析是建立在孔周土體中土顆粒始終保持緊密接觸的假設之上，即存在一定的誤差，但這種誤差會隨著與樁孔邊緣距離的增大而減小。

4 結語

該文根據滲流與固結理論，分析了樁基孔內抽水引起的樁孔周圍地表沉降的計算方法，工程實踐表明該計算方法具有一定的實用性。

在樁孔邊緣近距離范圍內，現場實測結果大于計算結果，推測這與分析計算時沒有考慮樁周土體中土顆粒的流失有關，在這方面有待改進。這也表明在分析樁周地表沉降時不可忽視樁周土體中土顆粒流失對地表沉降的影響。

［1］ 王一新，姚小平，孫榮玲.大跨度上承式拱橋施工監控技術［J］.河南理工大學學報：自然科學版，2014，33（2）.

［2］ 周益軍，高燕希，楊進.隧道開挖時地下滲流場的模擬分析［J］.公路與汽運，2008（4）.

［3］ 溫世儒.基于超前地質預報的隧道施工期風險評估及防控措施研究［D］.西安：長安大學，2012.

［4］ 賈強，張鑫，應惠清.樁基礎托換開發地下空間不均勻沉降的數值分析［J］.巖土力學，2009，30（11）.

［5］ 袁聚云，錢建國，張宏鳴，等.土質學與土力學［M］.北京：人民交通出版社，2010.

［6］ 徐春華，孫建波.樁基融沉附加力三維問題的積分方程解法［J］.施工技術，2012（增刊1）.

［7］ 陳希哲.土力學與地基基礎［M］.北京：清華大學出版社，2004.

［8］ 苑蓮菊，李振栓，武勝忠，等.工程滲流力學及應用［M］.北京：中國建材工業出版社，2001.

［9］ 錢家歡，殷宗澤.土工原理與計算［M］.北京：中國水利水電出版，1996.

［10］ 韓煊，李寧.隧道施工引起地層位移預測模型的對比分析［J］.巖石力學與工程學報，2007，26（3）.

［11］ 燕建龍，趙治海，楊利全，等.基坑降水設計中水文地質參數計算方法分析探討［J］.工程勘察，2011（3）.

U443.1

A

1671-2668（2016）06-0213-04

2016-02-20