基于數值試驗的波浪載荷激勵船舶振動響應研究

唐宇航， 陳志堅， 張佳棟

(海軍工程大學 艦船工程系，武漢 430033)

?

基于數值試驗的波浪載荷激勵船舶振動響應研究

唐宇航， 陳志堅， 張佳棟

(海軍工程大學 艦船工程系，武漢 430033)

即使未發生砰擊振動和顯著非線性波激振動，船體由較低頻波浪誘導產生的振動響應中依然存在高頻振動分量且高頻振動衰減緩慢。從單自由度系統簡諧激勵振動理論入手，指出響應解析解中常被忽略的伴隨自由振動項是導致高頻振動的一個因素，在系統阻尼較小、自振頻率較低時瞬態響應成分短時間內難以衰減，推導了位移、速度、加速度和內力響應中高頻成分的占比規律。分析了波浪載荷作用于船體時 “時變、場變” 的性質，及船舶小阻尼系統的特點，認為伴隨自由振動在波浪載荷激勵振動響應預報領域中有重要地位，對比時域法和頻域法在理論基礎上的差異，發現了時域法在處理該問題時的優越性。通過對雙體船進行數值仿真，結合海浪資料對該船16個航行工況的振動響應進行預報，結果表明各振動響應中均存在穩態高頻分量且占比較高，得出了高頻分量與頻率比關系的規律性結論，為時域中波激振動的進一步研究提供了思路。

伴隨自由振動；動力響應；高頻振動；時域法；非線性；波激振動

如今，關于船舶在波浪載荷作用下的振動描述主要包括砰擊振動和波激振動。砰擊振動是船舶在瞬時波浪沖擊載荷下引起的顫振，是以船舶固有頻率衰減的自由振動現象，持續時間不長；波激振動則是波浪激勵下引起的船體諧和振動現象，持續時間較長。根據北大西洋和西北太平洋的海浪統計資料，常見波浪周期一般不低于3.5 s，即使再考慮船-波的相對運動，那么波浪載荷所對應的遭遇頻率一般也不會高于船體一階總振動頻率。波激振動有線性(船體梁一階總振動頻率等于或接近遭遇頻率)和非線性(船體梁一階總振動頻率等于遭遇頻率的整數倍n)之分[1]。因此，由低頻波浪載荷所激起的船體高頻振動(以遭遇頻率為基準)，往往僅認為是由砰擊振動[2]或其與非線性波激振動的組合導致的。

用于評價船體振動響應水平的振動衡準特征參數一般是位移、速度、加速度和應力[3]。有資料表明，在實船測試、波浪載荷作用下的模型試驗中均發現，在各種不同波浪載荷條件下，均存在船體高頻振動響應比較劇烈的現象，產生嚴重的疲勞問題[4]。結合波浪載荷工況，對這類響應參數的時域信號進行幅頻響應分析時發現一種情況，即使船舶首階固有頻率遠遠大于波浪遭遇頻率，往往在近十倍以上，仍然存在比較顯著的高頻振動分量(以加速度響應最為明顯)，幅頻曲線中的響應峰值位置對應船體一階、甚至多階固有頻率，然而在該工況下的實船測試和模型試驗中卻均未發現船體砰擊現象。直覺上可以認為產生了非線性波激振動，但這種認識與非線性波激振動的當前定義不一致，即n為整數倍且該整數較小時非線性波浪荷載中某階倍頻成分才容易激起船體共振[5]，此外，非線性波激振動往往只是指船體的一階共振。可見，船體在波浪載荷作用下高頻振動響應問題需要進一步研究。

為解釋低頻波浪荷載作用時船體存在高頻振動響應成分的原因，探究不同振動衡準特征參數響應對波浪載荷相對頻率(相對于船體固有頻率)的敏感程度，分析不同波浪遭遇頻率下，船體高頻振動響應在總振動響應中的占比規律。本文從結構動力學基本理論入手，發現伴隨自由振動是引起高頻振動的一個重要因素，人們一般認為該振動會隨時間延長而衰減，常常很少關心它，但對于“既時變又場變”的波浪載荷，這種瞬態響應在理論預報和工程實踐中的作用卻有重要地位，從而為低頻波浪下船體存在穩態高頻振動找到了理論依據。同時結合目前該領域的研究方法，即頻域法和時域法，分析出時域法在處理非線性問題中的優勢，文中以雙體船為背景進行仿真計算并結合其航行、振動特點，將時域法應用在數值試驗中，對所得響應數據進行處理，從而得到了一些有意義的結論。

1 單自由度系統簡諧激勵振動理論

1.1 運動微分方程

波浪載荷對船體的激勵在一個較短的時間內，可認為是簡諧變化的，船體產生特定的振動(兩節點總振動)可認為是單自由度的，因此使用簡諧激勵作用下單自由度系統響應理論進行研究是合適的。

單自由度系統在簡諧激勵下的振動方程[6]：

(1)

式中，M為體系的質量；K為體系的剛度；C為體系的阻尼系數；P(t)為簡諧干擾力；P0為激勵力幅值；ω為激勵力頻率；β為激勵力的相位角。

對于黏性小阻尼系統，上述方程的通解形式為:

(A1cos(ωt+β)+A2sin(ωt+β))

(2)

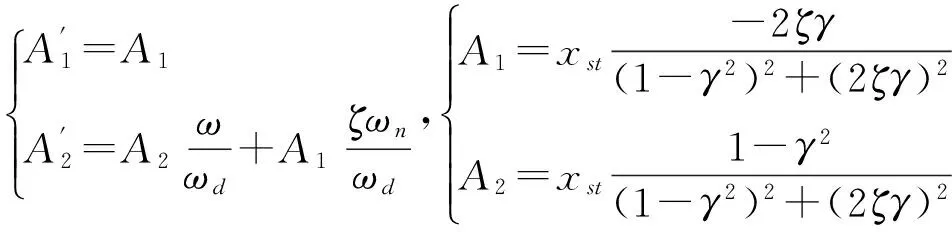
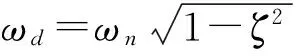
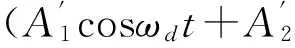
1.2 伴隨自由振動項與強迫振動項的幅值對比

伴隨自由振動響應的衰減項決定衰減速率，非衰減項決定初始振幅的大小。RX、RV、RA和RF分別表示位移、速度、加速度和內力的伴隨自由振動振幅與強迫振動振幅之比[7]，ηX、ηV、ηA和ηF分別表示位移、速度、加速度和內力的伴隨自由振動振幅與總振幅之比。由于船舶是小阻尼系統，模態阻尼一般不超過5%，所以在推導中會用到ζ?1且ζ2≈0的條件，RX、RV、RA和RF的簡要推導如下：

(3)

(4)

則：

(5)

(6)

則：

(7)

[mω2A1cos(ωt+β)+(P0-mω2A2)sin(ωt+β)]-

(8)

則：

(9)

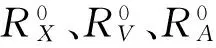
1.3 伴隨自由振動占比的討論

結合已有研究并考慮避免砰擊，重點對5、6級海況中特定波浪所誘導的波浪激勵進行計算，依據GWS的北大西洋 8、9、15及16四海區的海浪長期統計資料NA-1C，查表估算得到最大概率波浪周期[8]，從而決定波浪的基頻范圍，同時考慮船-波相對運動的多普勒效應，并以船舶模態阻尼系數中低阻尼曲線為參考，相關參數范圍選取見表1。

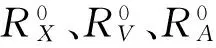
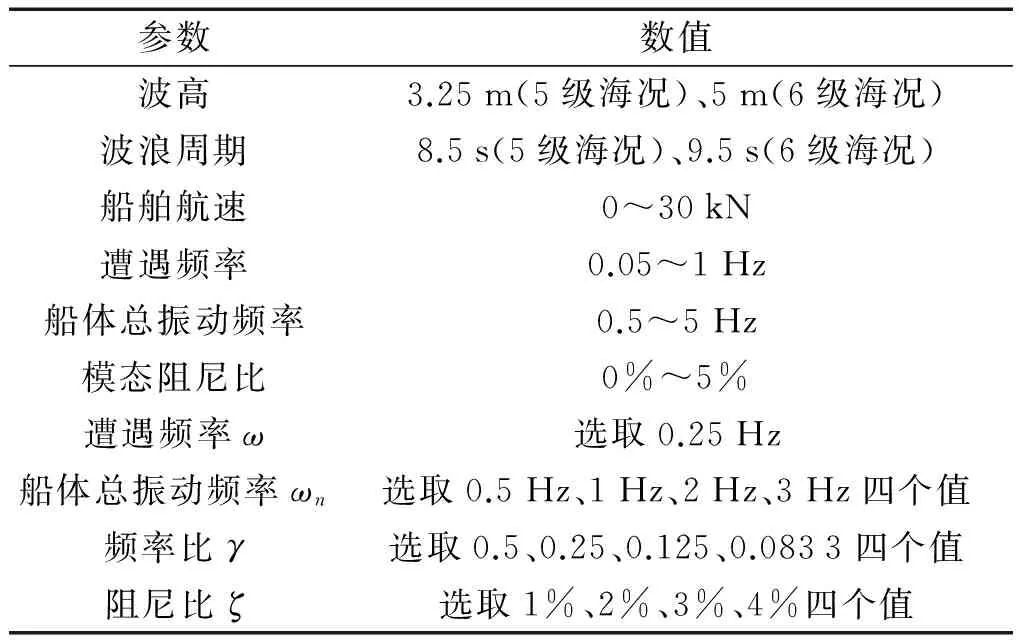
表1 波浪參數及相關參數可行范圍Tab.1 Wave parameters and practicable scope of relevant parameters

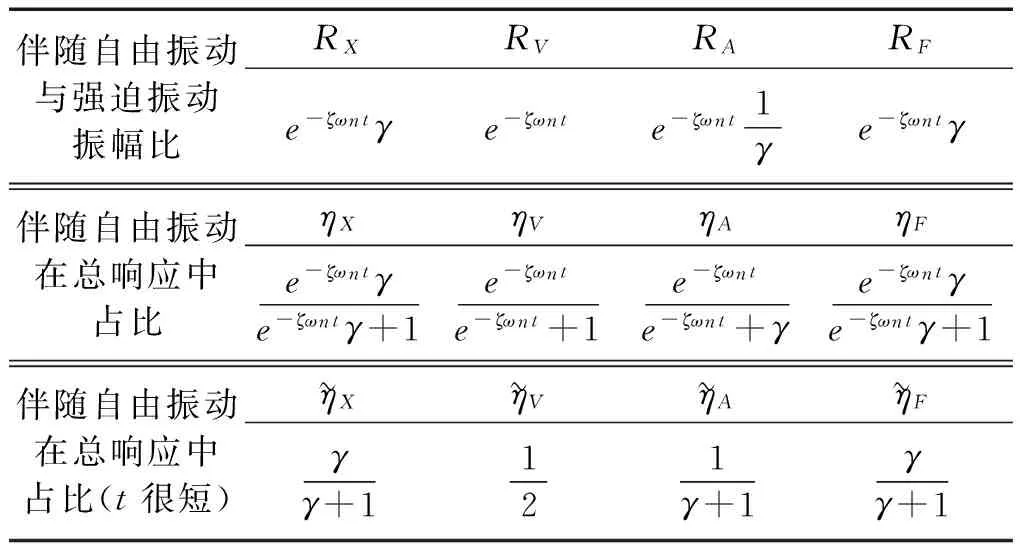
表2 計算公式匯總Tab.2 Summary of formulas

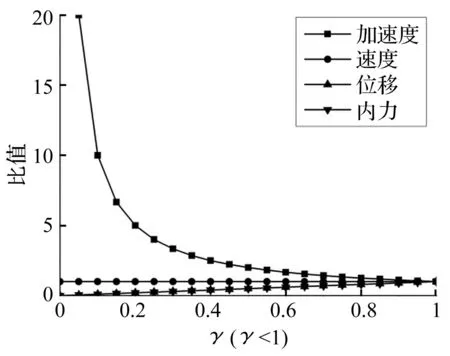
圖和隨γ(γ<1)的變化規律Fig.

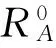
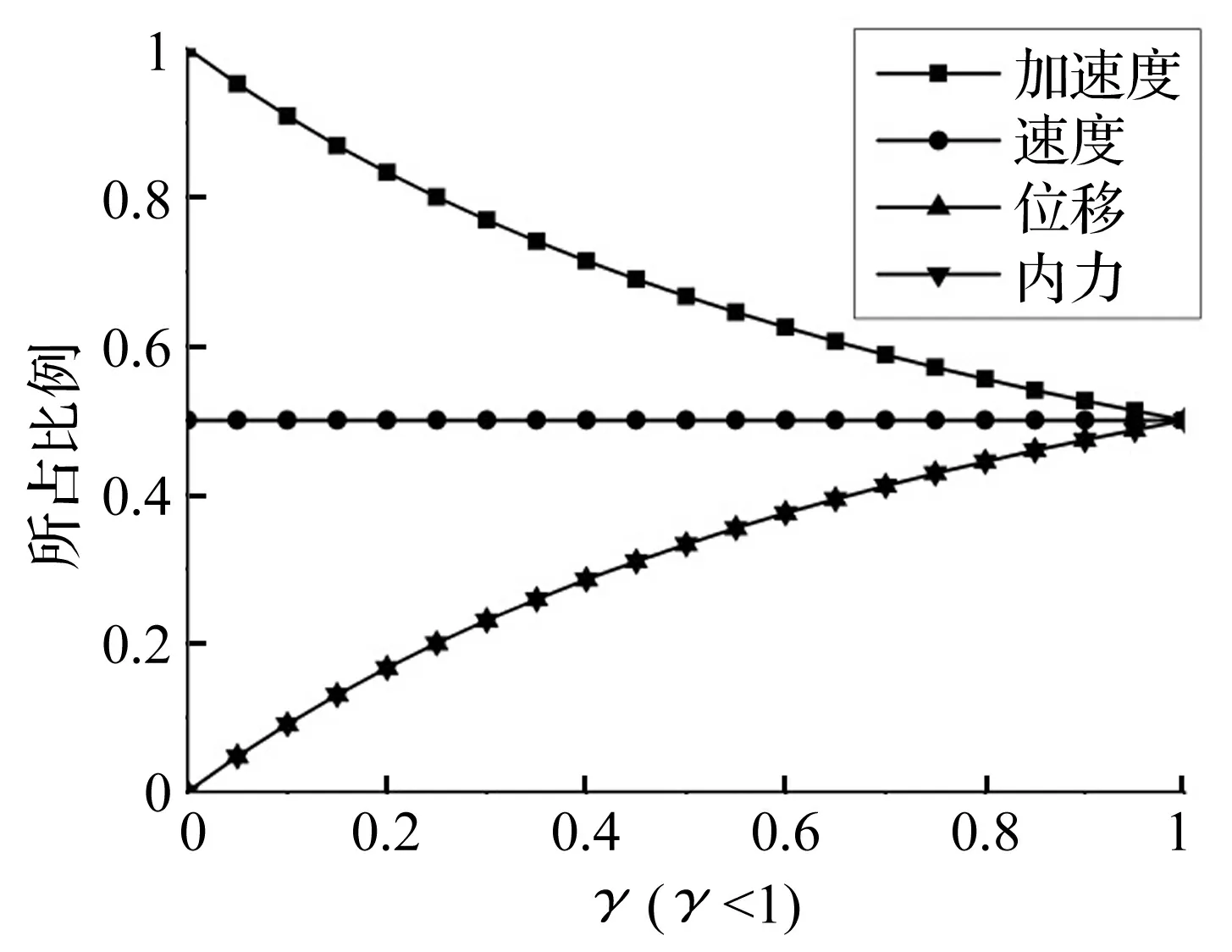
圖和隨γ(γ<1)的變化規律Fig.

γ<1時，加速度響應中伴隨自由振動成分在短時間內一直較大，選擇對加速度響應衰減進行時間歷程分析。依據表1參數，相同荷載頻率、不同阻尼比、不同自振頻率下的ηA隨時間(覆蓋多個波浪周期，取40 s)的變化歷程在圖3中給出。可以看出，阻尼越大衰減速度越快；在頻率比γ<1范圍內，即使存在阻尼的作用，伴隨自由振動成分也沒有衰減到可以忽略的地步，甚至可以認為伴隨自由振動在一定時間范圍內起主導作用。

以上的討論是基于單自由度體系下的理論推導，不能完全一致地適用于多自由度體系的響應預報，但是其規律性方面值得參考，可以推廣至多自由度體系的研究中。

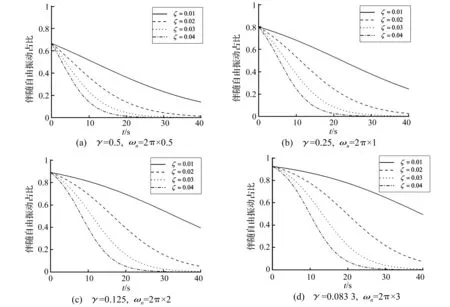
圖3 伴隨自由振動在加速度總響應中占比ηA隨時間的衰減曲線 (每個圖中4條曲線從上到下分別對應于ζ=0.01、0.02、0.03、0.04)Fig.3 Attenuation curve of acceleration response in the proportion of the total response (ηA) with time

2 理論預報研究方法

目前關于波浪激勵下船體振動響應研究，主要采用三維水彈性理論進行預報，但大多數是在頻域上進行[9]，該方法常在線性理論極值和非線性特性不顯著的疲勞損傷預報時采用，計算相對簡單快捷；而時域法可考慮波浪載荷及系統幾何非線性，更適合處理瞬態問題、時歷響應及船體大幅運動的非線性問題，分析精度高[10]，但其在波浪載荷預報領域的發展和應用還不夠成熟[11]。以下對頻域法和時域法的差異進行理論分析。

對多自由度體系進行動力反應分析時常使用模態疊加法，以實現向單自由度體系運算的轉化，該方法既可以在時域上進行，也可以在頻域上進行，但是各自的理論基礎和適用范圍均有差異。以位移疊加法為例，振型疊加法(模態疊加法)將各階振型位移的貢獻疊加起來，即：

x(t)=φ1Y1(t)+φ2Y2(t)+…+φNYN(t)

(10)

式中,Yn(t)為每一階振型的總反應。

(1)在時域中，每一階振型總反應可由Duhamel積分表示，即：

(11)

其中，

(0<ζn<1)

(12)

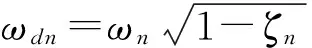
hn(t-τ)可以由單自由度體系下的阻尼單位脈沖反應函數類比獲得。對于低臨界阻尼體系，除了由微分沖量所引起的自由振動反應按指數衰減外，黏滯阻尼體系在一般動力荷載下反應推導與無阻尼情況完全相同。無阻尼體系中，對于任意一般荷載p(t)，在t=τ時作用的載荷強度為p(τ)，短時間dτ內載荷在結構上產生的沖量為p(τ)dτ，該沖擊荷載造成的反應近似分析如下。

短時沖擊荷載作用下，結構在很短時間內達到最大反應，此期間阻尼力來不及從結構中吸收太多能量，因此只需討論沖擊載荷下體系的無阻尼反應。對于質量m的沖量-動量關系可以寫成：

(13)

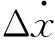
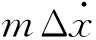
(14)

加載結束后反應為自由振動：

(15)

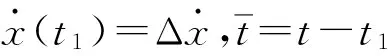
(16)

從時域法的推導過程中可以發現，該方法是對短時間沖量p(τ)dτ進行反應計算，反應是以瞬態自由振動為解，在時域上進行積分，充分考慮了dτ時間內系統的自由振動效應。Msc.nastran中瞬態響應計算正是對應于時域法，通過數值計算將連續積分離散化，計算多個時間步長下的累積響應，可以將伴隨自由振動考慮在內。

(2)在頻域中，每一階振型總反應:

(17)

式中，Pn(iω)為復荷載函數，是Pn(t)的Fourier變換。復荷載函數Pn(iω)和復頻反應函數Hn(iω)如下表達：

(18)

(ζn>0)

(19)

疊加法中多自由度系統的復頻反應函數與單自由度類似，由以下推導求出。

使用指數形式對穩態諧振反應求解，描述諧振荷載一般情況為:

(20)

本研究取相位角β=0，方程的特解為：

x(t)=Geiωt

(21)

解出常復數G為：

(22)

復頻反應函數H(iω)就是由G除以載荷幅值以后給出。

分析中發現，頻域法在求解運動微分方程時，忽略了簡諧荷載作用下式(20)的通解，即伴隨自由振動項，它僅考慮了特解，即強迫振動項。頻域法是一種針對固定幅值、固定位置的諧振響應計算方法，頻率響應分析用于計算結構在簡諧載荷作用下對每一個計算頻率的動響應；而時域法則將有初始條件的自由振動和伴隨自由振動考慮在內，瞬態響應分析可以用于計算時變、場變激勵載荷作用下結構的動力行為，方便地處理非線性運動問題。

一般情況下，認為自由振動部分會隨時間的延長而趨于衰減，常常很少關心它，但這一般是針對系統阻尼和自振頻率較高、初始條件恒定的問題而言[12]。但對受波浪作用的船體，在載荷作用的每個變化周期內，波浪在船體水線附近的作用位置(濕表面)是變化的，即力的作用點是“場變的”，此外，這部分船體濕表面所受的波浪力是隨時間變化的、是非連續的，即力的大小和方向是“時變的”。因此，對于波浪中航行的船舶而言，波浪激勵力既是“時變的”、同時亦是“場變的”，每一時刻都存在一個新的初始條件，對應每一時刻的初始條件，將產生一個新的伴隨自由振動，由于船舶是一個小阻尼系統，瞬態反應不易于衰減，是多個伴隨自由振動相疊加。那么在相當長一段時間中，伴隨自由振動項大小起主要作用，所以在有必要通過時域法探究伴隨自由振動對總振動的影響，以及低頻波浪載荷與船舶高頻振動響應的關系，從而進一步認識高頻振動響應的重要性。

3 數值仿真試驗

3.1 有限元計算模型

雙體船具有與常規單體船不同的結構形式，振型多樣也更為復雜[13]，總振動頻率較為密集，因此研究波浪載荷引起的高頻振動對雙體船而言意義更為重要。雙體船模型相關尺度見表3，依據模型資料按照《小水線面雙體船指南》要求構造全船有限元模型，各層甲板、艙壁板和舷側板等都采用板單元來模擬，橫梁、縱桁和肋骨等采用梁單元模擬，有限元模型的網格尺度按一個縱骨或一個肋位間距的小者劃分[14]。為確保準確地模擬船體結構，精確地計算船體整體和局部瞬態響應，所有對船體強度及振動有影響的因素都加以考慮。全船有限元模型如圖3所示，共有95 760個節點，212 518個單元。

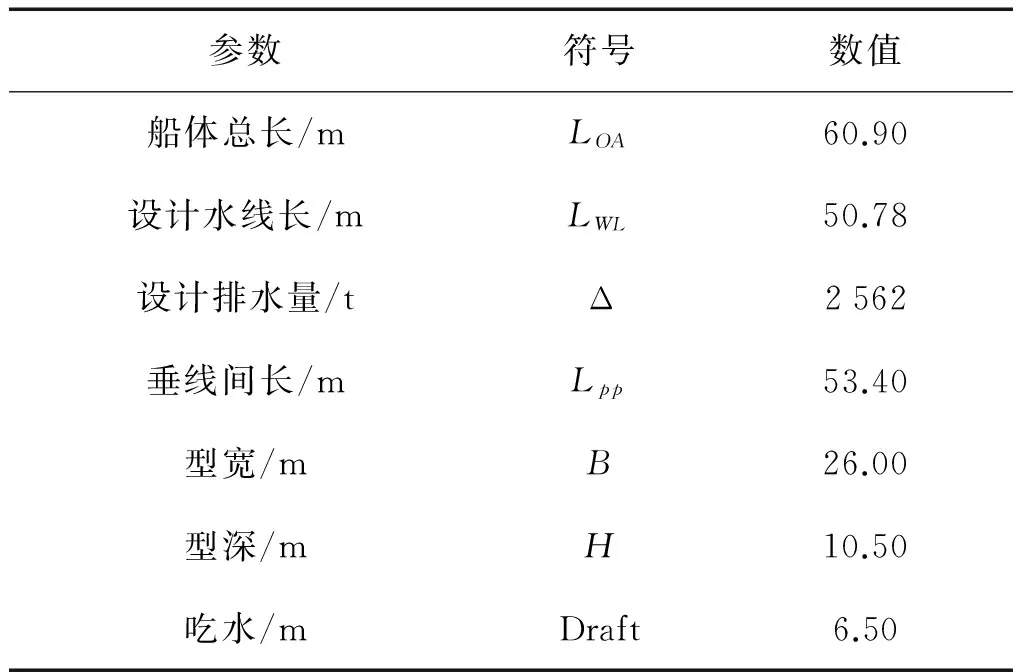
表3 計算模型的參數Tab.3 Parameters of calculate model

圖4 有限元整船模型Fig.4 Whole ship finite element model

3.2 計算波浪載荷和試驗工況設計

波動壓力以面壓力的方式直接作用在整船有限元模型的濕表面上，將波浪載荷函數轉換成Nastran中用PCL語言描述的Field場函數進行加載，同時采用虛質量法考慮流固耦合效應，即實現了整船有限元模型計算的工況構建[15]。僅考慮單項或線性波浪激勵，船舶的高頻響應可能會被嚴重低估[16-17]，因此本文采用基于有限幅波理論的波面函數的3階顯式表達式[18]：

(23)

設雙體船表面在有限幅波中航行時所受到的脈動壓力為p(x,y,t)，根據伯努利方程得：

pS(x,y,z,t)+pR(x,y,z,t)+pW(x,y,z,t)+

pD(x,y,z,t)

(24)

式中，a為波幅；k為波數；ΦW為入射波勢；ΦR為輻射波勢；ΦD為繞射波勢；ps(x,y,z,t)為船體運動而引起的流體靜水壓力的變化，pR(x,y,z,t)為船體運動而引起的輻射壓力；pW(x,y,z,t)為入射波引起的波浪壓力，即波浪主干擾力；pD(x,y,z,t)為因船體對入射波的限制而引起的繞射壓力。

在1.3節中提到，本文按實際海浪觀測資料決定波浪激勵力的基頻和波高參數，重點對5級、6級海況進行分析，波高由各級海況波高的上下限均值來決定，分別為3.25 m和5m。NA-1C海浪長期統計資料的有義波高為三參數的Weibull分布、跨零波浪周期為log-normal分布。其有義波高的Weibull分布為：

(25)

式中，H1=3.041，j=1.484，H0=0.66。跨零波浪周期的log-normal分布為：

(26)

計算波浪取最大概率波浪，即在本級海況有義波高條件下，波浪周期有最大發生概率p(tz/hs)的規則波，p(tz/hs)按式(26)進行計算，這是在平穩海況中最易遭到的波浪，表4中列出了5級、6級海情下波浪參數和概率。表5中給出了16個計算工況，其中包括5級海情下0 kN、6 kN和12 kN航速，180° 、135°、90°和0°浪向角的12個組合工況，6級海情下12 kN航速，180° 、135°、90°和0°浪向角的4個組合工況。

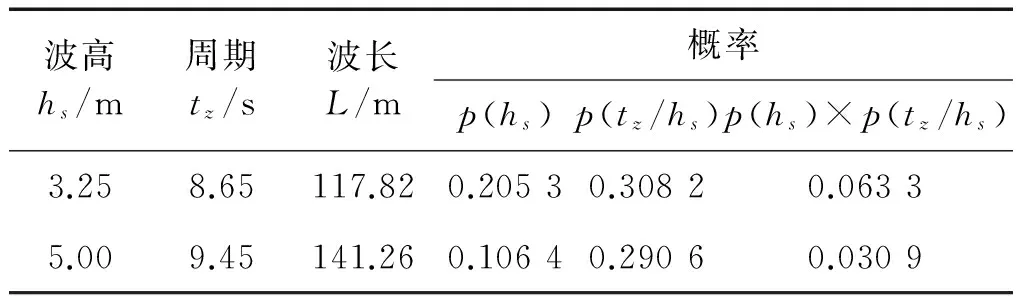
表4 波浪參數及發生概率計算表Tab.4 Wave parameters and occurrence probability calculation table

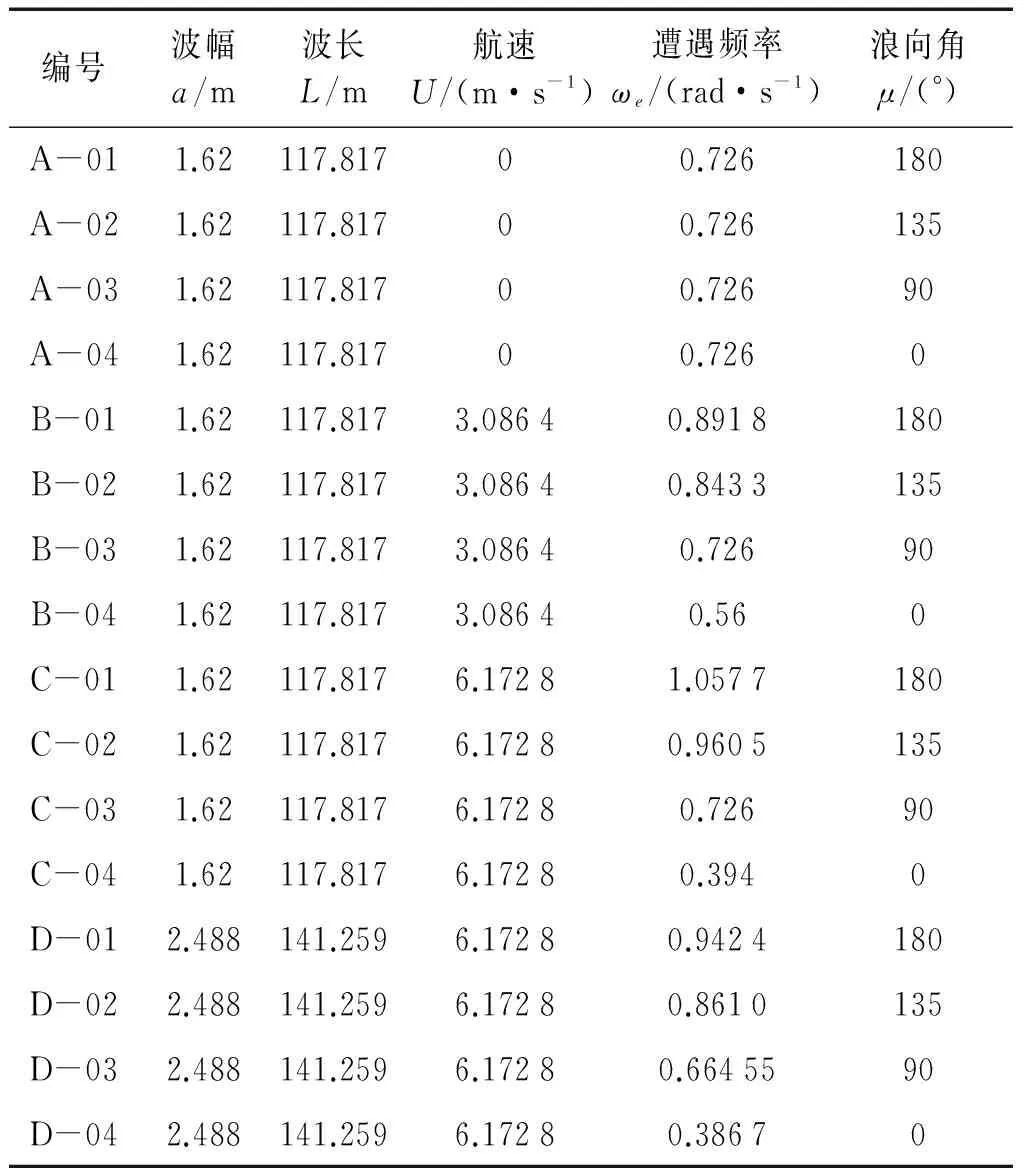
表5 數值仿真試驗計算工況Tab.5 Calculation conditions of numerical simulation experiment

3.3 仿真試驗結果分析

應用Msc.Nastran對整船有限元模型進行模態分析，得出干模態固有頻域和濕模態固有頻率，其中計算濕模態時通過虛擬質量法考慮船體濕表面與靜水的耦合作用，計算結果見表6。采用瞬態響應分析對船體動響應進行預報，參考《水面艦艇振動評價基準》中關于評價區域的要求，選取1甲板艉端左舷邊位置(node 32 346)分析，計算總時長42 s。

圖5為D-03工況下1甲板艉端左舷邊(node 32 346)位移響應合成、高頻和低頻時間歷程曲線，其中存在重要的高頻分量。黑色為合成成分，藍色為高階成分，紅色為波頻成分。D-03工況下1～3倍遭遇波頻分別為0.105 8 Hz(即0.664 55 rad/s)、0.211 6 Hz和0.317 5 Hz，對node 32 346的位移響應時域信號進行低通濾波，得到0.4 Hz以下的波頻信號成分，為穩定的有限幅波3階波頻合成成分。該船總振動首階頻率為2.576 3 Hz，再對node 32 346的位移響應時域信號進行高通濾波，得到2 Hz以上的高頻信號成分，包含了該船總振動頻率下高階成分。圖6為D-03工況下node 32 346的位移響應頻譜分析圖，圖中低頻波浪荷載導致的0.4 Hz以下的低頻分量，同伴隨自由振動導致的按固有頻率振動的高頻分量在量值上相當。從圖5中可以看出在計算的40 s內高頻分量沒有顯著的衰減，而此時的1～3倍波浪遭遇頻率和該船首階總振動頻率之比分別為γ=0.041、0.082和0.123，說明在船舶首階固有頻率遠大于波浪遭遇頻率(近十倍以上時)、不會發生非線性波激振動的情況下，仍存在高頻振動響應比較顯著的現象，換句話說即使有阻尼的存在，其伴隨自由振動響應導致的高階振動也難以在短時間衰減，從而不能被測試和分析所忽略。

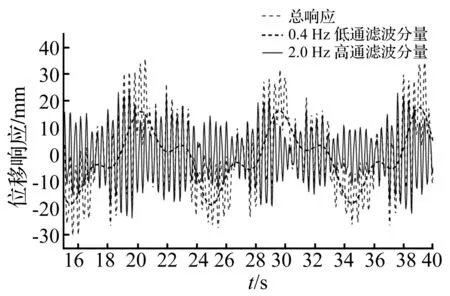
圖5 D-03工況1甲板艉端左舷邊位移響應合成、 高頻和低頻時間歷程曲線(15～40 s)Fig.5 Tine series of total, high and low frequency displacement on the port side of the 1st deck trailing edge for case D-03 (15～40 s)

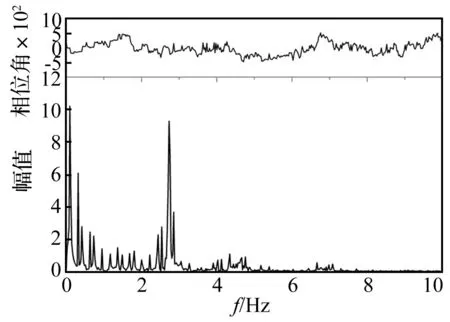
圖6 D-03工況1甲板艉端左舷邊位移響應的頻譜分析圖Fig.6 Spectrum of time-displacement waveform on the port side of the 1st deck trailing edge for case D-03

圖7～圖10 為C-02工況node 32 346位置處位移、速度、加速度和應力響應的頻譜分析圖。C-02工況中波浪遭遇頻率為0.152 9 Hz，頻率比γ=0.059，即使是3倍波浪遭遇頻率，該船首階自振頻率也是其五倍以上。圖7～圖9給出了位移、速度和加速度響應頻譜圖，波頻(低頻)成分響應分量占比依次減小，反之，伴隨自由振動(高頻)成分響應分量占比依次增大，圖8中可見低頻分量幾乎為零，說明在頻率比比較小(γ<1)時，高頻成分在加速度總響應中占比最大，其次是速度響應，再次是位移響應。由于在施加波浪壓力時存在常數項，因此圖10中在0 Hz處存在一個非零初始值，若僅考慮波動部分，可得應力低頻響應與高頻響應的占比規律與位移響應規律一致。對C-02工況下node 32 346處各響應衡準參數的時域信號進行濾波，可得到低頻波浪誘導的低頻振動分量(0.5 Hz以下)和伴隨自由振動誘導的高頻振動分量(0.5 Hz以上)，表7給出了各響應參數的低、高頻成分占比結果，可見伴隨自由振動誘導的高頻振動成分占比很大，尤其是加速度響應。結合1.3節對單自由度系統中伴隨自由振動占比的討論，結果表明與多自由度的船舶系統相比，各自的伴隨自由振動分量占比在量值上存在差異，但總體規律一致。此外，在該船舶系統中，伴隨自由振動分量在總響應中占比整體較大，存在“放大”效應。

表6 仿真試驗計算的雙體船整船總振動頻率和振型結果Tab.6 Simulation calculation results of catamaran total vibration frequencies and mode shapes

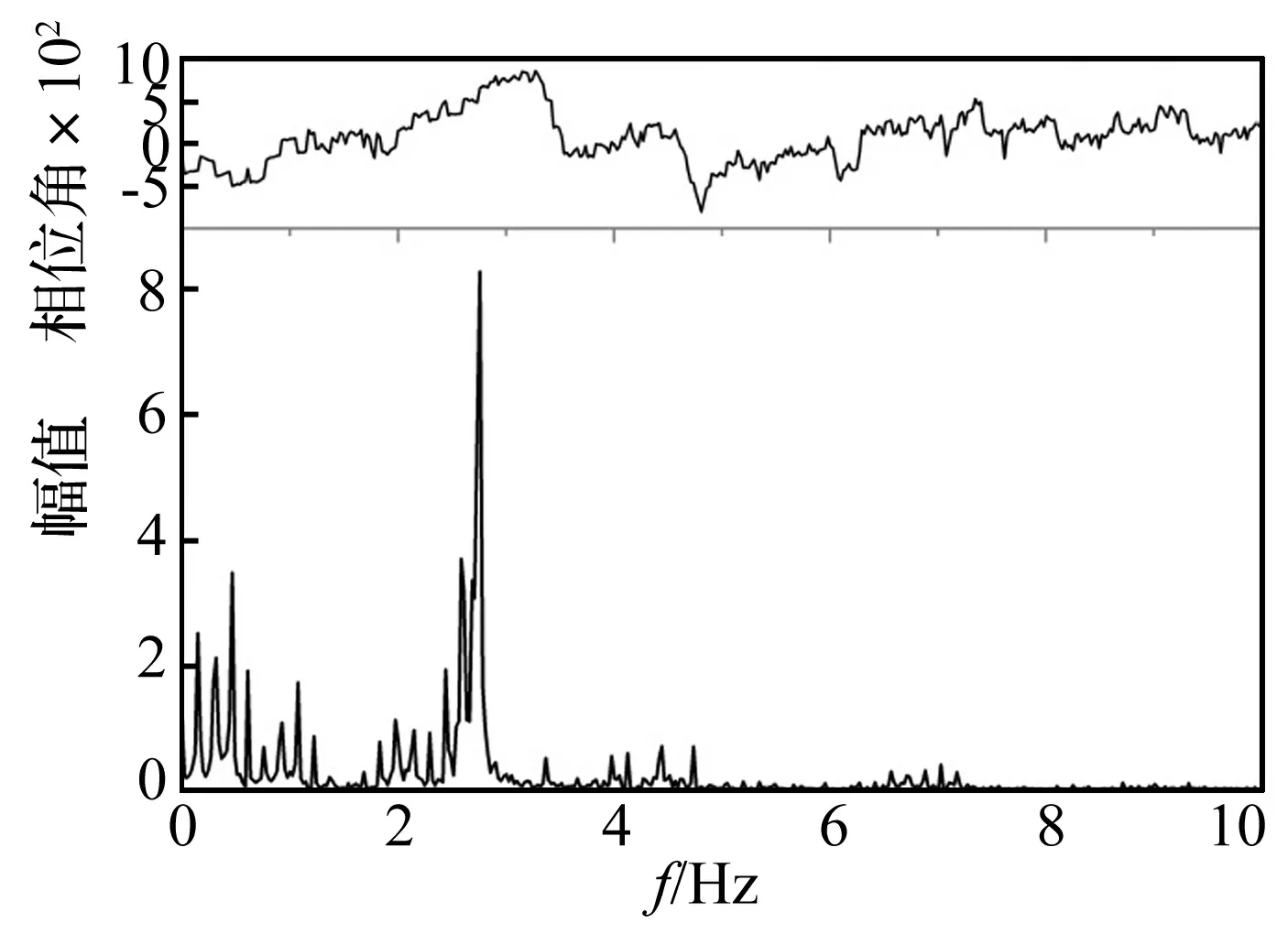
圖7 C-02工況node 32 346位置處位移響應的頻譜分析圖Fig.7 Spectrum of time-displacement waveform of node 32 346 for case C-02

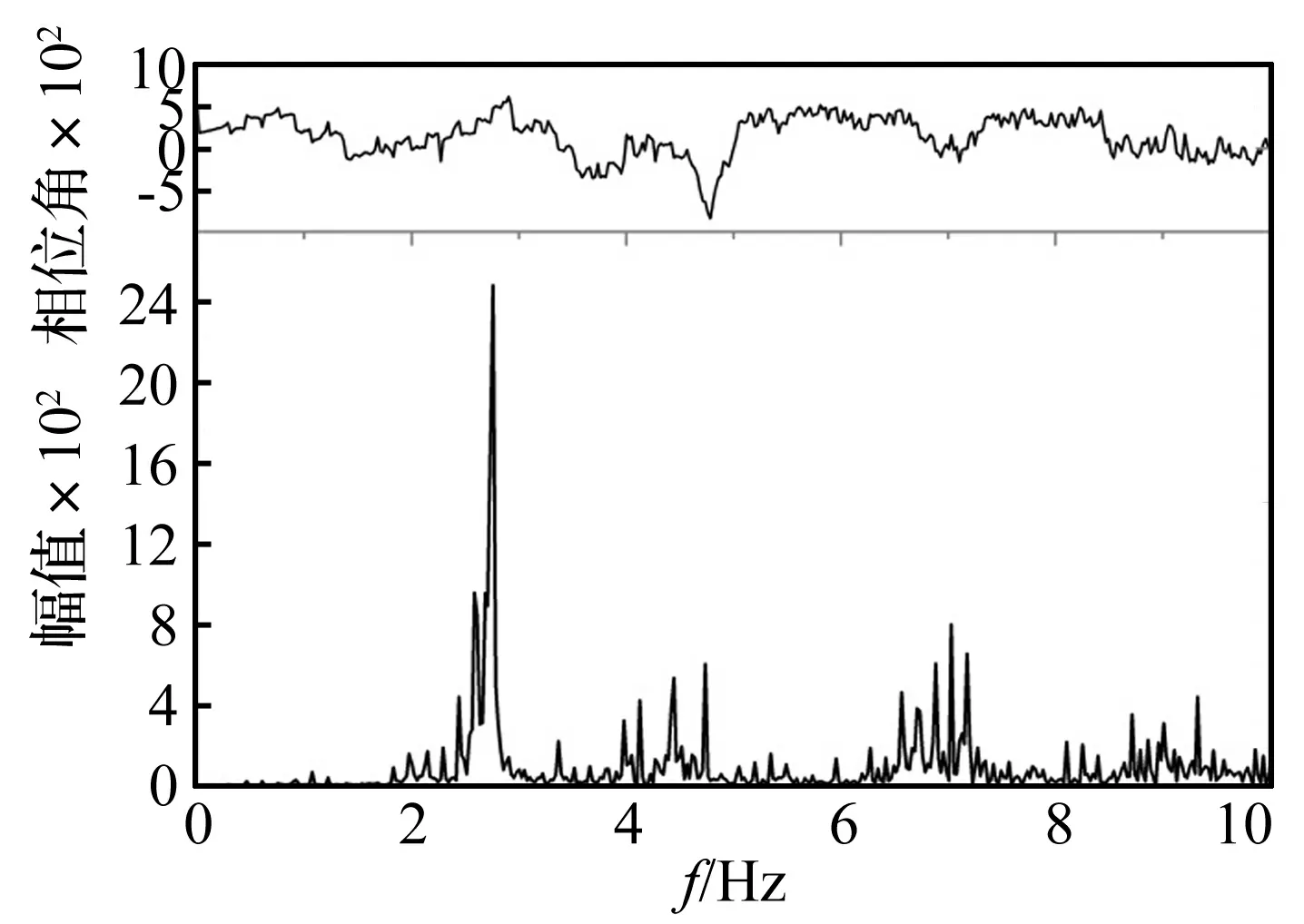
圖9 C-02工況node 32 346位置處加速度響應的頻譜分析圖Fig.9 Spectrum of time-acceleration waveform of node 32 346 for case C-02

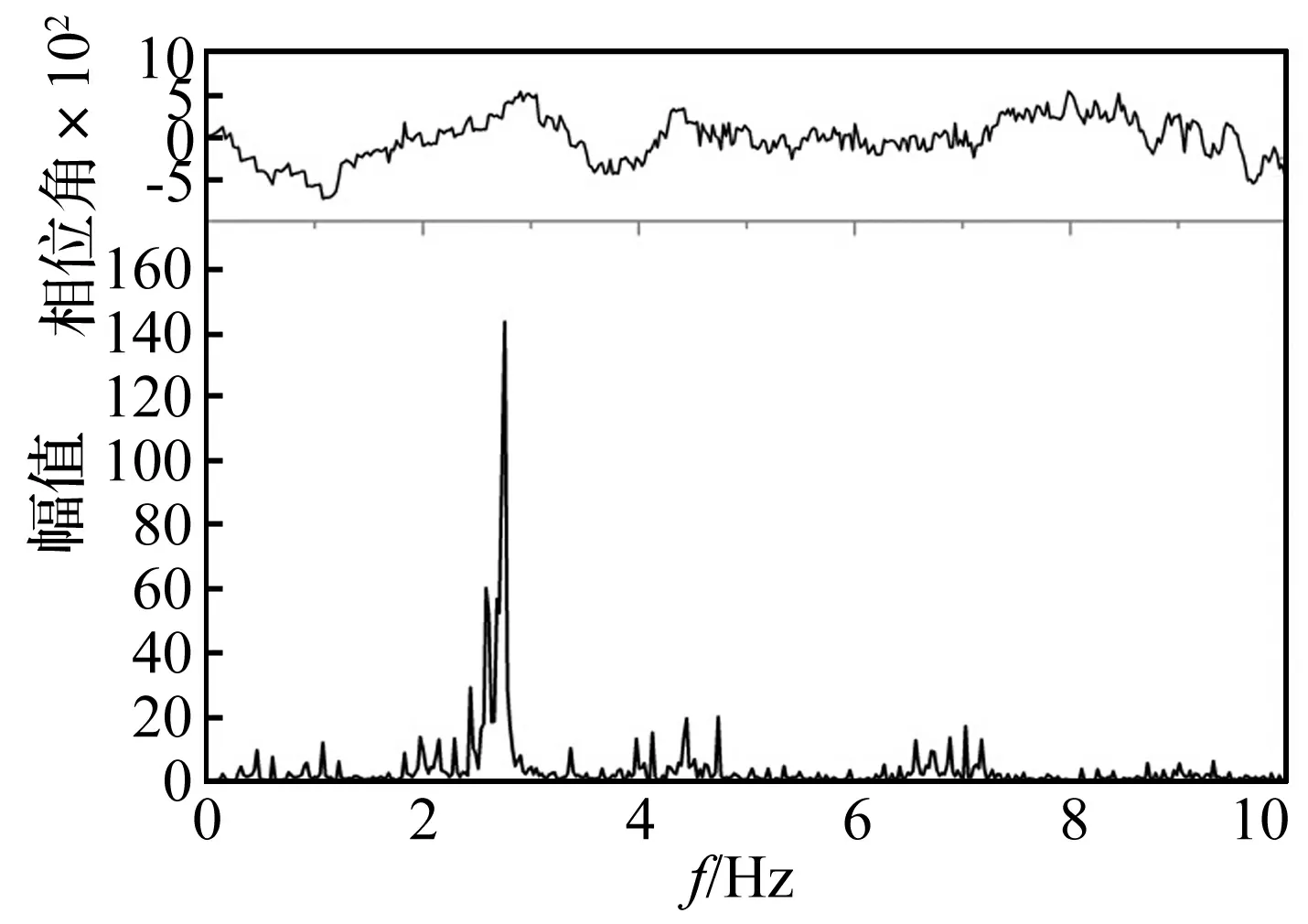
圖8 C-02工況node 32 346位置處速度響應的頻譜分析圖Fig.8 Spectrum of time-velocity waveform of node 32 346 for case C-02

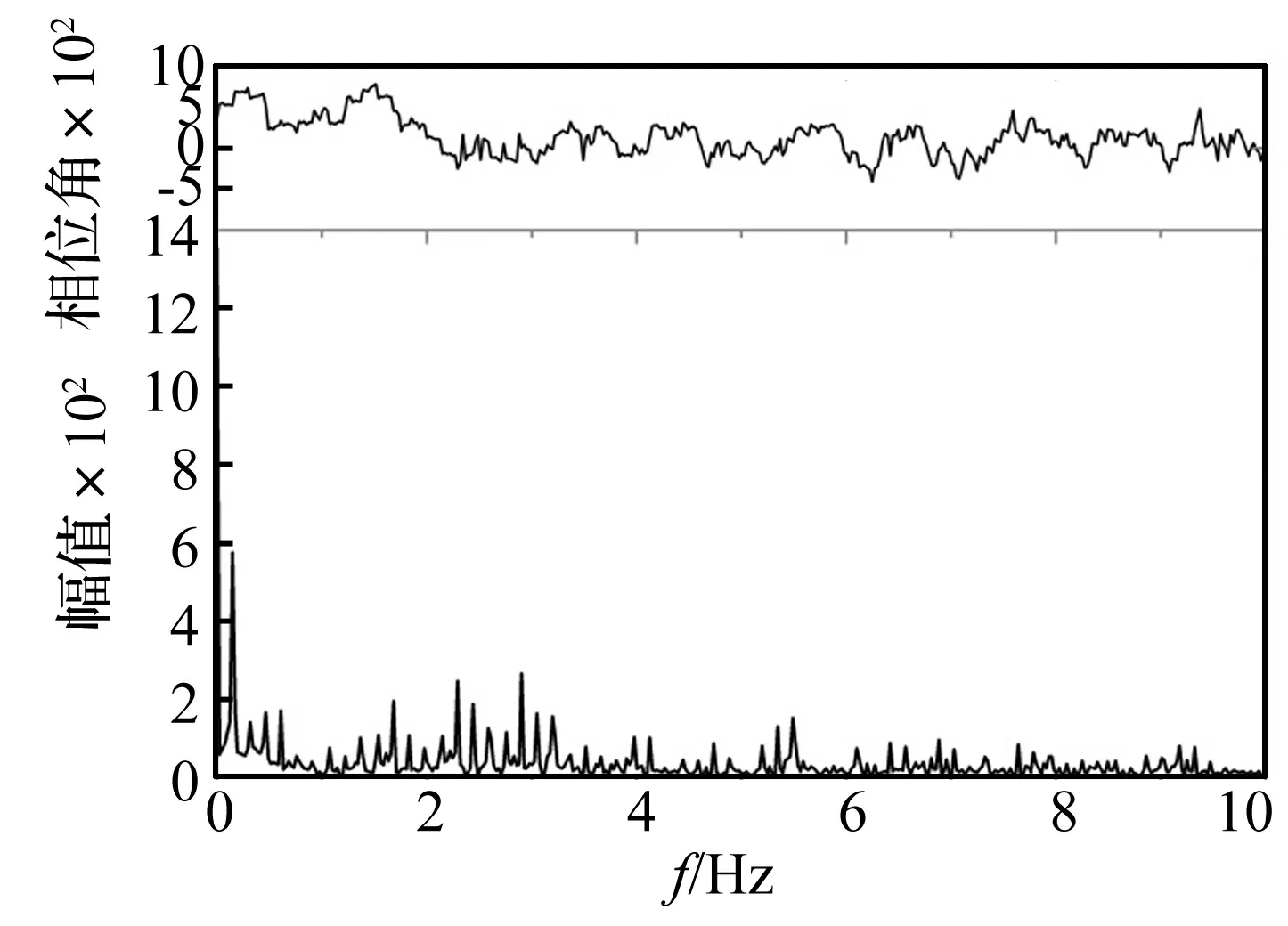
圖10 C-02工況node 32 346位置處應力響應的頻譜分析圖Fig.10 Spectrum of time-stress waveform of node 32 346 for case C-02表7 C-02工況各振動衡準參數中低頻、高頻成分占比分析(node 32 346)Tab.7 Analysis of the proportion of low and high frequency in each vibration criteria parameters for case C-02(node 32 346)

響應時域最大值0～0.5Hz內的低頻成分低頻成分占比/%0.5Hz以上的高頻成分高頻成分占比/%高頻成分低頻成分位移響應/mm27.499.3934.1618.1065.841.93速度響應/(mm·s-1)325.2917.485.37307.8194.6317.61加速度響應/(mm·s-2)965318.260.199634.7499.81527.64應力響應/kPa2466.61764.2330.981702.3869.022.23

注：分析應力響應低、高頻成分占比時僅考慮波動部分。

圖11～圖13給出了相同波浪參數、不同航速下node 32 346處位移響應，計算工況為A-01、B-01和C-01，遭遇頻率分別為0.726 rad/s、0.891 8 rad/s和1.057 7 rad/s，該船頂浪航行的01工況易于激起“兩潛體垂向彎曲”模態(模態頻率為4.72 Hz)，則頻率比依次為γA-01=0.024、γB-01=0.03和γC-01=0.071，從圖中可以看出，隨著頻率比γ的增大高頻振動響應所占比重也增大。對時域計算結果進行濾波處理后計算數據見表8。應力響應與位移響應有同樣的規律。

表8 A-01、B-01和C-01工況位移響應中低頻、高頻成分占比分析(node 32 346)Tab.8 Analysis of the proportion of low and high frequency in displacement response for case A-01,B-01 and C-01(node 32 346)

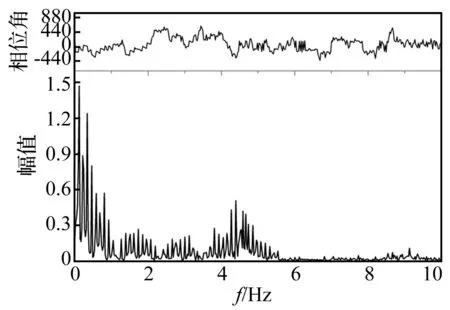
圖11 A-01工況node 32 346位置處位移響應的頻譜分析圖Fig.11 Spectrum of time-displacement waveform of node 32 346 for case A-01

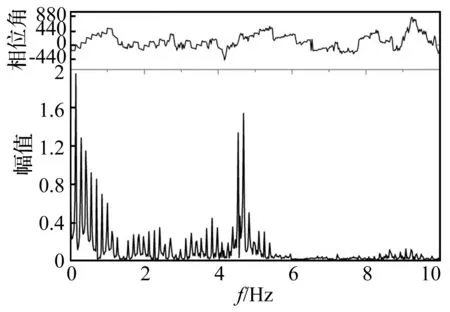
圖12 B-01工況node 32 346 位置處位移響應的頻譜分析圖Fig.12 Spectrum of time-displacement waveform of node 32 346 for case B-01

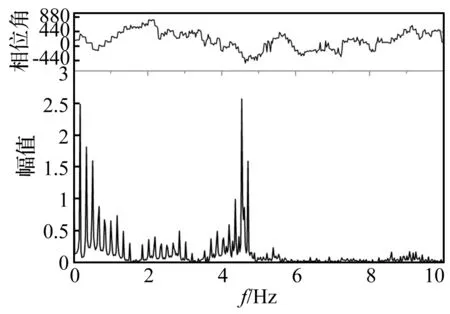
圖13 C-01工況node 32 346 位置處位移響應的頻譜分析圖Fig.13 Spectrum of time-displacement waveform of node 32 346 for case C-01

4 結 論

目前關于波浪激勵下的船舶動響應研究主要集中在砰擊振動和波激振動上，然而由低頻波浪誘導產生的船體穩態高頻振動問題卻難以解釋。本文從單自由度理論體系出發，對上述高頻振動的形成機理進行研究，明確了伴隨自由振動在小阻尼體系中短時間內難以衰減的事實。另外，考慮波浪載荷作用于船體時“時變、場變”的特殊性，采用可以將伴隨自由振動考慮在內的瞬態響應分析方法，結合NA-1C海浪長期統計資料，對該船在5、6級海況下16個航行工況的振動響應進行預報，分析各振動衡準參數中高頻成分占比的相關規律。得到如下結論：

(1)低頻波浪所誘導的船體高頻振動不易于衰減，是因波浪荷載作用時“時變、場變”的性質所致，加之以船舶是個小阻尼系統，簡諧載荷激勵所產生的伴隨自由振動難以在短時間內衰減，形成相對穩態的高頻振動。

(2)在頻率比比較低(γ<1)時，由低頻波浪載荷激勵產生的船體振動響應中，位移、速度、加速度和應力響應均存在顯著的高頻成分，該成分在各響應中的占比不同，占比最大的是加速度響應的高頻成分，其次是速度響應，再次是位移和應力響應。但是，雖然不同振動衡準特征參數響應中的高頻成分在比例上有所差別，其量值均沒有小到可以忽略的程度。

(3)在相同海況下，波浪遭遇頻率的大小線性決定頻率比γ的大小，從位移響應計算結果中發現，其振動總響應中的高頻成分占比隨γ的增大而增大，愈加成為振動的主要成分。進一步分析，隨頻率比增加，當遭遇頻率(或者其較低幾階的倍頻)接近船舶自振頻率時，船舶可能發生一般意義的非線性波激振動，同時考慮到伴隨自由振動不可忽略，那么此時由波浪誘導的高頻振動分量則應該認為是伴隨自由振動與非線性波激振動的疊加，該結論在理論預報中值得考慮。

因此，這種從伴隨自由振動的角度考慮高頻振動的方法，為低頻波浪激勵下的高頻波激振動響應研究開發了新思路。

[1] 汪雪良,顧學康,胡嘉駿.船舶波激振動研究進展[J].船舶力學,2013,17(7):830-844. WANG Xueliang, GU Xuekang, HU Jiajun. A state-of-the-art review on ship’s springing investigation [J]. Journal of Ship Mechanics, 2013,17(7):830-844.

[2] 夏齊強，陳志堅，李科技. SWATH船在砰擊載荷作用下動態響應研究[J].振動與沖擊，2011，30(6)：208-212. XIA Qiqiang, CHEN Zhijian, LI Keji. Dynamic response of SWATH under slamming loads [J].Journal of Vibration and Shock, 2011，30(6)：208-212.

[3] 陳志堅.艦艇振動學[M].北京:國防工業出版社,2010,4: 229-230.

[4] GU X K, SHEN J W, MOAN T. Experimental and theoretical investigation of higher order harmonical components of nonlinear bending moments of ships[J].Journal of Ship Technology Research, Schiffstechnik, 2000, (4): 143-154.

[5] 顧雪康,胡嘉駿.超大型油船模型波浪載荷試驗報告[R].無錫：中國船舶科學研究中心科技報告,2004.

[6] 克拉夫 R, 彭津 J. 結構動力學[M]. 北京:高等教育出版社,2006,11:27-34.

[7] 祁皚，范宏偉，陳永祥. 簡諧荷載作用下伴生自由振動的研究[J].地震工程與工程振動, 2002,22(6):156-161. QI Ai, FAN Hongwei, CHEN Yongxiang. Research on transient vibration under input of harmonic loading [J]. Earthquake Engineering and Engineering Vibration, 2002, 22(6):156-161.

[8] 戴仰山,沈進威,宋競正. 船舶波浪載荷[M]. 北京:國防工業出版社,2007,1:11-21.

[9] JENSEN J J. Stochastic procedures for extreme wave load predictions-wave bending moment in ships[J]. Marine Structures, 2009, 22: 194-208.

[10] 劉秀全,陳國明,暢元江,等. 基于頻域法的深水鉆井隔水管波激疲勞分析[J].振動與沖擊,2013,32(11):7-11. LIU Xiuquan, CHEN Guoming, CHANG Yuanjiang, et al. Wave-loading fatigue analysis for deep water drilling risers in frequency domain [J]. Journal of Vibration and Shock, 2013, 32(11):7-11.

[11] 葛菲. 非線性波浪載荷作用下多種應力成份組合的船體結構疲勞強度分析[D].哈爾濱:哈爾濱工程大學,2004.

[12] 繆紅燕,高金吉,徐鴻. 轉子系統瞬態響應不平衡的有限元分析[J].振動與沖擊,2004,23(3):1-4. MIAO Hongyan, GAO Jinji, XU Hong. Transient response of unbalanced rotor system through its critical speed [J]. Journal of Vibration and Shock,2004,23(3):1-4.

[13] 葉永林,席亦農,尤國紅,等. 小水線面雙體船總振動計算與試驗研究[J].中國造船,2011,52(4):56-65. YE Yonglin, XI Yinong, YOU Guohong, et al. Overall vibration calculation and test for swath ship [J]. Shipbuilding of China, 2011,52(4):56-65.

[14] 中國船級社. 小水線面雙體船指南(2005)[M].北京：人民交通出版社，2007,2:40-41.

[15] 夏齊強,陳志堅,孫春生. 鋁合金穿浪雙體船波激振動響應計算研究[J].艦船科學技術,2010,32(2):11-16. XIA Qiqiang, CHEN Zhijian, SUN Chunsheng. A study on wave-induced vibration for aluminum alloy wave piercing catamarans [J]. Ship Science and Technology, 2010, 32(2):11-16.

[16] VIDIC-PERUNOVIC J, JENSEN J J. Non-linear springing excitation due to a bidirectional wave field [J]. Marine Structures,2005, 18: 332-358.

[17] VIDIC-PERUNOVIC J. Springing response due to bidirectional wave excitation[D]. Technical University of Denmark, 2005.

[18] 文圣常,于宙文. 海浪理論與計算原理[M].北京:科學出版社,1985,11:96-101.

Vibration response analysis of ships under wave load based on numerical experiment

TANG Yuhang, CHEN Zhijian, ZHANG Jiadong

(Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China)

Even if the slamming vibration and significantly nonlinear wave-induced vibration do not occur, in the vibration response of the hull induced by low-frequency wave load, there still exist high-frequency vibration components, which decay slowly. Based on the harmonic vibration analysis of single-degree of freedom system, it is indicated that the associated free vibration which is often overlooked in the analytical response solution is one of the high-frequency vibration factors. The transient response component is difficult to decay when the system damping is small and natural frequency is low. The occupied proportions of high-frequency components in the responses of displacement, velocity, acceleration and internal force were derived. The “time-changing and field-changing” characteristics of wave loads acting on ships were revealed. It is also shown that the associated free vibration plays an important role in the prediction of vibration responses excited by wave loads. The differences between the results by time domain and frequency domain methods were discussed and the advantages of time-domain methods in dealing with this issue are more prominent. The vibration responses in 16 sailing conditions were forecasted by the numerical simulation of a catamaran, using the wave data. The results show the high-frequency components in the vibration responses are both of steady-state and high-proportion. The relationship between high-frequency components and frequency ratio was obtained, which provides a guideline for the further study on wave-induced vibration in time domain.

associated free vibration; dynamic response; high-frequency vibration;time domain method; nonlinear; wave-induced vibration

國家自然科學基金(51479205)

2015-12-14 修改稿收到日期：2016-03-16

唐宇航 男，博士，1991年生

陳志堅 男，教授，博士生導師，1957年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2016.22.018