水下復雜應力結構的固有頻率研究

楊 念， 陳爐云， 易 宏， 劉 勇

(1.上海交通大學 船建學院海洋工程重點實驗室，上海 200240； 2. 中船重工第七〇二研究所上海分部，上海 200011)

?

水下復雜應力結構的固有頻率研究

楊 念1， 陳爐云1， 易 宏1， 劉 勇2

(1.上海交通大學 船建學院海洋工程重點實驗室，上海 200240； 2. 中船重工第七〇二研究所上海分部，上海 200011)

研究水下結構物的復雜應力狀態對結構固有頻率的影響，克服以往研究中只考慮整體均勻分布應力的局限性。水下結構因外部環境特殊常常處于復雜應力狀態，復雜應力與流固耦合的共同作用使結構的固有頻率求解變為一個耦合非線性特征值問題，以往求解流固耦合的方法不再適用于此類問題。有限元方法也能處理此類問題，但存在處理過程復雜、計算量大、不能明確說明結構應力與動力特性之間的本質物理聯系等缺點。針對該問題用理論方法進行了分析，首先基于Flügge殼體理論、考慮流固耦合作用、利用特定模態之間的正交性建立復雜應力結構自由運動方程，然后采用多項式近似結合二次型矩陣線性化的方法對此類結構的固有頻率進行求解。在數值算例中，計算了某水下圓柱殼的固有頻率，并對比和分析了不同類型的復雜應力對于水下結構固有頻率的影響特點。

復雜應力；流固耦合；結構振動；固有頻率

隨著水下工程結構的復雜化及工作環境的特殊性，在承受工況載荷之前，結構中往往已經存在著一定的應力。這些應力中有些是人為施加的，如橋梁、土木結構中施加的預應力；有些是在實際加工過程中不可避免的，如焊接殘余應力、結構制造缺陷、熱效應等；有些是結構因外部工作環境而產生的，如潛艇殼體中因外部水壓力而產生的殼體應力、立管因復雜深海環境而產生的管體應力等。這些應力雖然產生原因和性質特點各有不同：前兩類應力是結構在不受外力情況下產生，其應力狀態是自平衡的；第三類應力則是因外力作用產生的，其應力狀態非自平衡，而是與外力平衡。但這些應力有一個共同點：均在結構承受工況載荷之前便已存在于結構之中，屬于廣義上的預應力。研究廣義預應力對結構固有頻率的影響是結構設計中的一個重要內容。

在廣義預應力結構的固有頻率研究方面，DOONG[1]采用根據高階剪切變形理論推導了含預應力矩形厚板的控制方程，并將計算得到的屈曲載荷和固有頻率與BRUNELLE等[2]進行了比較。高永毅等[3]對有、無殘余應力的平板的固有頻率進行了對比實驗，經實驗驗證殘余應力使構件固有頻率發生變化。FUNG等[4]采用對振動位移在時間和空間上進行級數展開的方法，分析得到了含預應力薄壁圓柱殼的固有頻率和振型。PENZES等[5]對于任意邊界條件的各向同向圓柱殼，推導了含初始扭矩、壓力、軸力以及轉動效應的自由振動精確解，并與實驗數據進行了比較。劉志忠等[6]研究了流體靜壓對圓柱殼頻散特性和功率流的影響。FULLER等[7]建立了充液圓柱殼的自由振動方程，研究了充液圓柱殼的頻散特性。張小銘等[8-9]利用波傳播方法分析了水下圓柱殼結構和充液圓柱殼結構的自由振動特性。朱大同[10]以兩端簡支、端頭有剛性平面限制的圓柱殼為例，計算了空殼和充液殼的頻率，討論了各階頻率與周波數的關系。

但目前在含廣義預應力結構動力學研究領域主要關注應力呈整體均勻分布的情況，對于局部復雜應力問題(應力幅值隨位置變化而變)的研究比較少。陳爐云等[11]和劉勇[12]分別運用變分原理和模態正交性開展了局部預應力對結構動力特性影響研究。盡管他們考慮了結構因復雜應力而產生的模態耦合，但并未考慮流固耦合的影響，因此結構自由振動方程仍是一個線性方程，求解相對容易。

但是，實際水下工程結構不僅應力狀態復雜，同時還要考慮流固耦合對固有頻率的影響，當同時考慮兩個影響因素時問題變得非常復雜：當結構應力非均布時，各個結構模態之間會發生耦合，導致不能對單個模態進行單獨的自由振動分析，而必須對整個耦合矩陣方程進行求解，得到耦合模態，張小銘等解決流固耦合結構振動的方法不再適用；如果再考慮流固耦合作用，又增加了非線性的問題，陳爐云等未考慮流固耦合的影響，其方法無法運用在水下結構物上。有限元方法[13]雖然能處理此類問題，但其不能明確說復雜應力與動力特性之間的本質物理關系、不便于我們對復雜應力的影響特點和規律進行研究。同時有限元施加指定分布應力的過程較為復雜、計算量大。

本文針對此問題，用理論方法進行了分析。考慮流固耦合作用，利用特定模態之間的正交特性，建立水下復雜應力結構自由振動方程，通過多項式近似結合二次型矩陣線性化的方法解決耦合矩陣的非線性特征值問題，計算并分析了不同類型的局部復雜應力對水下結構物固有頻率的影響特點。

1 理論分析

1.1 基本方程

本文以圓柱殼為例，推導水下復雜應力結構動力學方程，其結構如圖1所示。

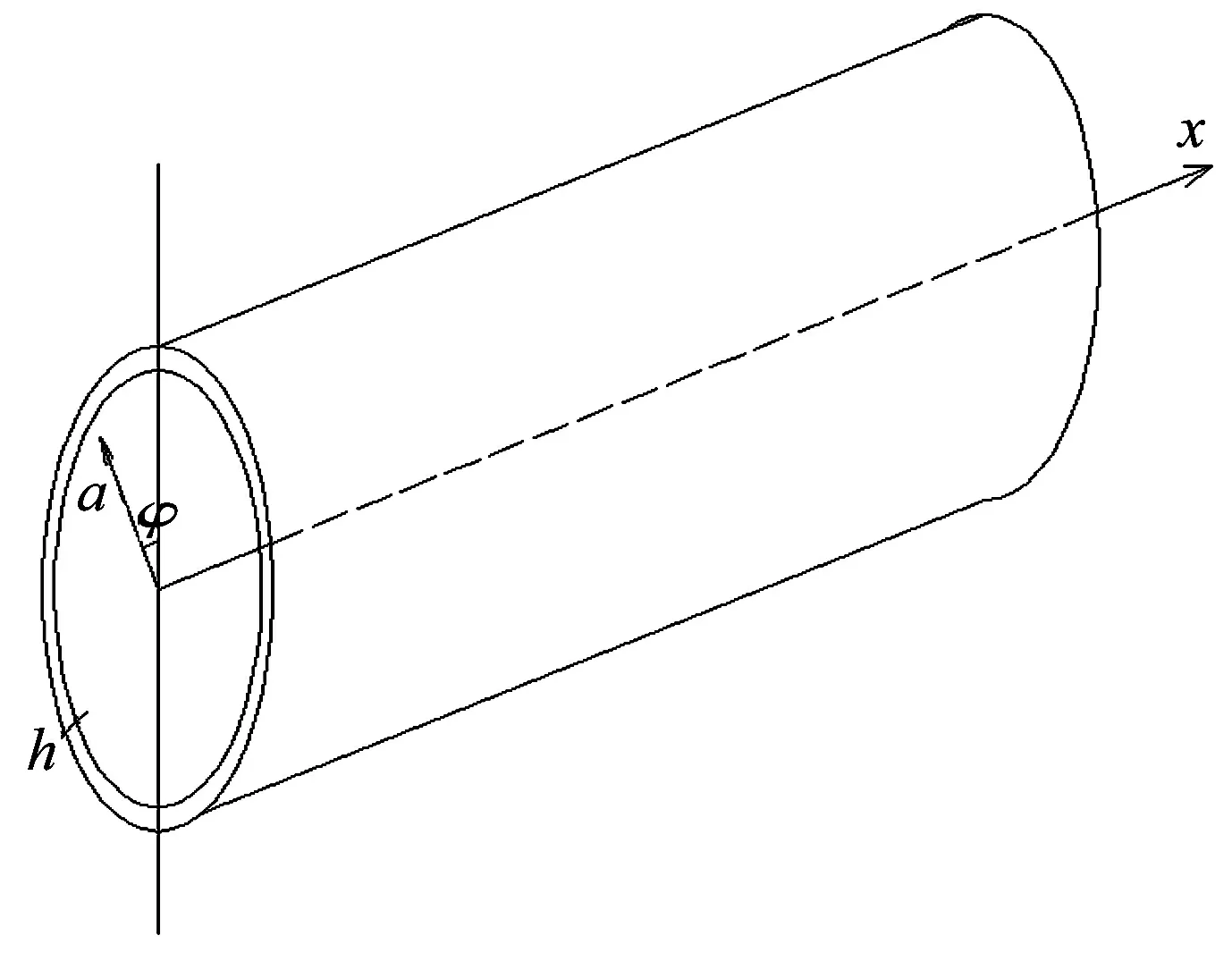
圖1 圓柱殼幾何模型Fig.1 Cylindrical shell

不考慮流固耦合時，復雜應力殼體自由振動控制方程為:

(1a)

(1b)

(1c)

假設圓柱殼長度為l，邊界條件為兩端簡支，滿足邊界條件的位移可以表示成如下級數形式[14]：

(2)

式中:λ=π/l。

將式(2)代入式(1)，然后將式(1a)等號兩邊同時乘以cos(mλx)和cos(nφ)，式(1b)等號兩邊同時乘以sin(mλx)和sin(nφ)，式(1c)等號兩邊同時乘以sin(mλx)和cos(nφ)，利用三角函數正交性得：

(3a)

(3c)

式中:a為圓柱殼半徑。式(3)即為不考慮流固耦合時復雜應力結構動力學控制方程。如果結構無應力，則通過正交性可實現全部解耦。但如果結構含應力，那應力項C1、C2和C3是不能解耦的，所以他們在式(3)中以積分形式存在，將這些積分項分別設為K1、K2和K3，它們即表征復雜應力對控制方程的影響。積分項K1、K2和K3的存在，表明各階結構模態之間出現了耦合，不能再單獨計算某一階結構模態，只能對整個耦合方程進行求解，以得到耦合模態。

1.2 考慮流固耦合影響

本文考慮結構浸沒在流體中的情況。考慮流固耦合作用后，需在式(1c)中加入流體對結構表面的壓力項Pf，式(1c)變為:

(1c’)

壓力項的表達式設為[15]:

(4)

由流體、固體在結構表面速度連續，即邊界條件為:

(5)

把位移、壓力項表達式帶入邊界條件得：

(6)

因此可用位移系數表示流體對結構表面的壓力項：

Pf=

則(3c)變為:

(3c’)

本文不考慮切應力，只考慮正應力。將復雜應力表達式設為:

(8)

將式(8)代入K1、K2和K3，利用正交性對K1、K2和K3進行處理(具體處理過程見附錄B)，處理后單階模態只和指定階模態發生耦合，和其他階模態之間可以實現解耦。最后將處理后的K1、K2和K3代入式(3)建立3M×N個方程，將其聯立為方程組并表示成矩陣形式:

(Λ+Rgj)X=0

(9)

式中:X={U1…U(m-1)×N+n…UM×N}T，U(m-1)×N+n=

當結構中應力形式更加復雜時，復雜應力可用級數形式表示：

(10)

按照上述相同的方法，可以建立3M×N個方程，將其聯立成方程組并表示為矩陣形式：

(Λ+R)X=0

(11)

復雜應力的級數項是線性相加關系，R可以表示為:

(12)

需要注意的是，大部分的分布函數(無論是自平衡還是非自平衡復雜應力的分布形式)都可以用本文提供的級數去擬合。因此對于實際結構中的自平衡和非自平衡復雜應力，本文方法均可適用。

1.3 自由振動

自由振動求解，令式(11)的系數矩陣行列式為零：

(13)

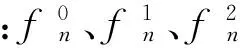
Λ+R=B0+B1·ω+B2·ω2

(15)

式中:B0包含泰勒展開中的常數項和復雜應力矩陣R；B1為泰勒展開中的ω的一次項系數矩陣；B2包含泰勒展開中的ω的二次項系數矩陣和未考慮流固耦合時的ω系數矩陣。這樣，原非線性特征值問題變為二次型特征值問題，用第一類伴隨矩陣對式(15)進行線性化處理[16-17]：

(16)

式中:I為單位矩陣。經過線性化處理后得到一般特征值問題(Generalized Eigenvalue Problem，GEP)，最后對此一般特征值問題進行求解得到固有頻率和耦合模態陣型。

2 算例分析

2.1 方法正確性驗證

表1 解析方法與有限元方法計算結果Tab.1 The result form analytical method and finite element method

圖2 圓柱殼模型圖Fig.2 Cylinder model

圖3 圓柱殼軸向預應力分布形式Fig.3 Cylindrical shell axial initial stress distribution

通過表1可以發現，有限元計算結果和解析方法計算結果基本吻合，從而驗證了本文方法的正確性。

2.2 算例模型

本節用本文方法計算某水下復雜應力結構的固有頻率，并分析不同分布的復雜應力對固有頻率的影響特點。需要說明的是，本文所有應力分布均屬于結構整體分布。所選用模型與2.1節相同。另外考慮流體影響，水的密度ρf=1 000 kg/m3；水中聲速c=1 500 m/s。

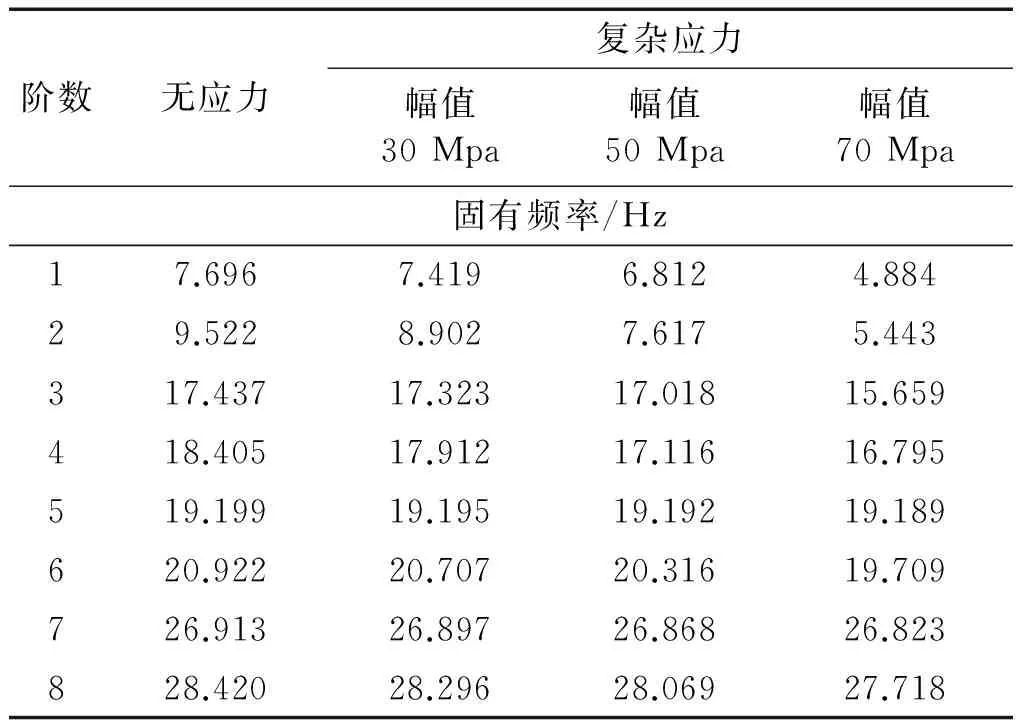
表2 固有頻率對比Tab.2 Natural frequency comparison

圖4 復雜應力分布圖Fig.4 Complex stress distribution

從表2可以看出復雜應力對水下圓柱殼自然頻率影響明顯，影響程度隨著應力幅值的增加而增大，因此當水下結構中的復雜應力幅值達到一定程度時，其對結構固有頻率的影響將不能忽視。以下各節將從不同方面研究不同類型的復雜應力對結構固有頻率的影響特點。為使問題研究更具針對性，2.3～2.5節均只考慮單向變化應力，并且都選用2.1節中的模型。

2.3 應力方向對固有頻率的影響規律研究

本節研究軸向與周向復雜應力對于結構固有頻率的影響規律。計算工況如表3所示，分別比較這幾種工況下結構的前八階固有頻率計算結果如表4所示。

表3 工況表Tab.3 Case table

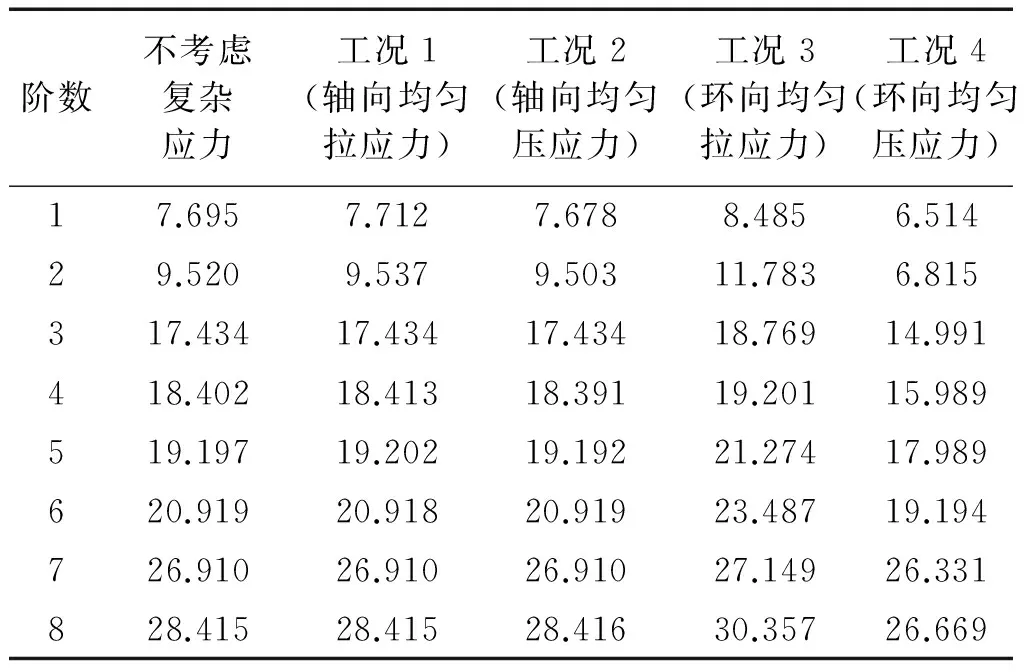
表4 固有頻率對比Tab.4 Natural frequency comparison

從表4可以看出，軸、環向拉應力使結構固有頻率上升，壓應力使結構固有頻率下降，這與相關文獻中得到的影響規律是一致的[18-21]。其中環向應力對固有頻率的影響更大，因此在實際水下工程中對圓柱殼結構應特別注意環向應力的控制。這一點容易解釋，結構在環向剛度更低，臨界應力更低，因而結構固有頻率對于環向應力的改變更為敏感。

2.4 復雜應力狀態與均勻應力狀態的結構固有頻率對比研究

本節研究復雜應力狀態與均勻應力狀態對結構固有頻率的影響。計算工況如表5所示，本節分別計算了結構在非自平衡復雜應力(模擬受外力結構應力狀態)及自平衡復雜應力下(模擬含預應力結構應力狀態)的固有頻率，并與2.3節中的代表均勻應力狀態的工況3、4進行比較。這幾種復雜應力分布形式均為三角函數，具體分布如圖5所示。比較這幾種工況下結構的前八階固有頻率，計算結果如表6所示。

表5 工況表Tab.5 Case table

表6 固有頻率對比Tab.6 Natural frequency comparison

圖5 應力分布圖Fig.5 Stress distribution

從表6可以看出，本節所選的復雜應力類型對結構固有頻率的影響程度相對于均勻應力略小，可能是因為所選復雜應力在作用區域積分后總的數值小于均勻應力的總值造成的。而總值相等、分布類型不同的復雜應力對結構的影響情況將在2.5節中進行詳細研究。此外，自平衡應力狀態下結構的固有頻率幾乎沒有變化，該現象同樣可用前面積分總值的理論進行解釋。可見，相較于均勻應力，接近實際結構應力狀態的復雜應力對結構固有頻率的影響特點更為復雜，有必要進行深入研究。

2.5 復雜應力分布形式對固有頻率的影響研究

本節研究不同分布形式的復雜應力對于結構固有頻率的影響。選用模型同前面一樣，計算工況如表7所示，復雜應力分布如圖6、7所示，工況13、14、15比較了幾種幅值相同、周期不同的復雜應力對固有頻率的影響；把工況16、17、18和2.4節中的工況5放在一起，比較了幾種應力集中度不同的復雜應力對固有頻率的影響，這三種工況的應力在結構區域內積分的數值相等。計算結果如表8所示。

圖6 應力分布圖1Fig.6 Stress distribution 1

圖7 應力分布圖2Fig.7 Stress distribution 2表7 工況表Tab.7 Case table

工況應力方向分布特征細化特征應力幅值/Mpa工況13環向自平衡復雜應力4個半波10工況14環向自平衡復雜應力8個半波10工況15環向自平衡復雜應力12個半波10工況5環向復雜拉應力應力集中度低10工況16環向復雜拉應力應力集中度中10工況17環向復雜拉應力應力集中度高10工況18環向均勻拉應力應力集中度最低20/π

表8 固有頻率對比Tab.8 Natural frequency comparison

從本節計算結果可以看出，在復雜應力幅值相同時，周期應力的周期大小對于結構固有頻率的影響不大。此外，當復雜應力在結構區域內積分總值相等時，應力集中度不同會在一定程度上影響：應力集中度越高，對固有頻率的影響越小。但總的說來，應力集中度對固有頻率的影響并不顯著。另外值得注意的是，應力集中度對固有頻率的影響雖不明顯，但對結構的其他性能(比如管壁應力極值、強度、穩定性)卻可能產生較大影響，實際結構中應當注意這方面的影響。

3 結 論

文章基于Flügge殼體理論，運用特定模態之間的正交關系，實現模態的部分解耦。并考慮流固耦合作用，推導了水下復雜應力結構自由振動方程，采用多項式近似結合二次型矩陣線性化的方法求解該非線性特征值問題。運用本文方法對不同類型復雜應力的影響情況進行了計算與分析，計算發現：環向應力對圓柱殼固有頻率影響更大，在實際水下工程中對圓柱殼結構應特別注意環向應力的控制；在作用區域內積分總值更大的復雜應力對結構固有頻率的影響更大；當應力積分總值一定時，應力分布周期及應力集中度對結構的影響不大；此外，自平衡復雜應力對結構影響較小，但這一點還不能完全確定，如3.1節中的復雜應力在作用區域內也是自平衡的，但其對結構的固有頻率仍有較大影響，因此復雜應力對結構的影響特點還需進行更加深入的研究。

通過本文研究表明，結構中存在的復雜應力會影響其固有頻率，不同類型的復雜應力其對于結構固有頻率的影響程度和特點不同，與均勻應力的情況相比更為復雜，需深入研究各類復雜應力所帶來的影響。實際工程結構物中的應力一般都為非均勻分布，以往只研究均勻分布應力對結構的影響遠遠不夠。在今后研究中應結合水下工程結構物的實際應力分布特點開展復雜應力結構動力學特性的研究。

[1] DOONG J L. Vibration and stability of an initially stressed thick plate according to a high-order deformation theory[J]. Journal of Sound and Vibration, 1987, 113(3): 425-440.

[2] BRUNELLE E J, ROBERTSON S R. Vibrations of an initially stressed thick plate[J]. Journal of Sound and Vibration, 1976, 45(3): 405-416.

[3] 高永毅，劉德順. 利用試驗模態分析進行殘余應力評估的研究[J]. 振動與沖擊, 2005, 24(5)：111-114. GAO Yongyi, LIU Deshun. Studies on estimation of residual stress using modal analysis[J]. Journal of Vibration and Shock,2005, 24(5)：111-114.

[4] FUNG Y C, SEEHLER E E, KAPLAN A. On the vibration of thin cylindrieal shells under intemal pressure[J]. Journal of the Aeronautical Science, 1957, 24(9): 650-660.

[5] PENZES L E, KRAUS H. Free vibration of initial stressed cylindrical shells having arbitrary homogeneous boundary conditions[J]. AIAA Journal, 1972, 10(10): 1309-1341.

[6] LIU Z, LI T, ZHU X, et al. The effect of hydrostatic pressure fields on the dispersion characteristics of fluid-shell coupled system[J]. Journal of Marine Science and Application, 2010, 9(2): 129-136.

[7] FULLER C R. The effects of wall diseontinuities on the propagation of flexural waves in cylindrieal shells[J]. Joumal of Sound and Vibration, 1981, 75(2): 207-228.

[8] ZHANG X M, LIU G R, LAM K Y. Vibration analysis of thin cylindrical shells using wave propagation approach[J]. Journal of Sound and Vibration, 2001, 239(3): 397-403.

[9] ZHANG X M, LIU G R, LAM K Y. Frequency analysis of cylindrical panels using a wave propagation approach[J]. Applied Acoustics, 2001, 62(5): 527-543.

[10] 朱大同. 充液圓柱殼的自振特性[J]. 力學學報, 1984, 16(2): 141-150. ZHU Datong. On the free vibration of a circular cylindrical shell filled with liquied[J].Theoretical & Applied Mechanics,1984, 16(2): 141-150.

[11] 陳爐云, 李磊鑫, 張裕芳. 含局部預應力的圓柱殼結構聲輻射特性分析[J]. 上海交通大學學報, 2014, 48(8): 78-64. CHEN Luyun, LI Leixing, ZHANG Yufang. Characteristics anylysis of structural-acoustic of cylinder shell with prestress in local areas[J]. Journal of Shanghai Jiao Tong University,2014, 48(8) : 78-64.

[12] 劉勇. 復雜預應力對圓柱殼結構動力特性影響研究[D]. 上海：上海交通大學, 2014.

[13] 熊健民，周俊榮，周金枝. 基于 ANSYS 預應力簡支梁固有頻率的研究[J]. 固體力學學報, 2008, 29: 158-161. XIONG Jianmin, ZHOU Junrong, ZHOU Jinzhi. Research of pre-stress simple-supported beam’s natural frequency based on ansys[J]. Chinese Journal of Solid Mechanics, 2008, 29: 158-161.

[14] 何祚鏞. 結構振動與聲輻射[M]. 哈爾濱：哈爾濱工程大學出版社, 2001.

[15] ZHANG X M. Frequency analysis of submerged cylindrical shells with the wave propagation approach[J]. Mechanical Science, 2002, 44(7): 1259-1273.

[16] KIRKUP S M, AMINI S. Solution of the Helmholtz eigenvalue problem via the boundary element method[J]. International Journal for Numerical Methods in Engineering, 1993, 36(2): 321-330.

[17] GIORDANO J A, KOOPMANN G H. State space boundary element-finite element coupling for fluid-structure interaction analysis[J]. The Journal of the Acoustical Society of America, 1995, 98(1): 363-372.

[18] 曹志遠. 板殼振動理論[M]. 北京: 中國鐵道出版社, 1989.

[19] 張耀庭，汪霞麗，李瑞鴿. 預應力梁固有頻率的試驗研究[J]. 華中科技大學學報, 2007, 35(2): 12-15. ZHANG Yaoting, WANG Xiali, LI Ruige. Experimental research on nature frequency of prestressed concrete beams [J]. Journal of Huazhong University of Science & Technology,2007, 35(2): 12-15.

[20] 張耀庭，汪霞麗，李瑞鴿. 全預應力梁振動頻率的理論分析與試驗研究[J]. 工程力學, 2007, 24(8): 116-120. ZHANG Yaoting, WANG Xiali, LI Ruige. Experimental and theoretical research on vibration frequency of full-prestressed concrete beam[J].Engineering Mechanics, 2007, 24(8): 116-120.

[21] 姜勁楓，王柏生. 預應力梁、板彎曲振動固有頻率的研究[C]// 第五屆全國結構工程學術會議論文集(第二卷),1996.

附錄A

L1,L2,L3,C1,C2,C3的具體表達式如下：

附錄B

附錄C

A(m-1)×N+n中的元素為：

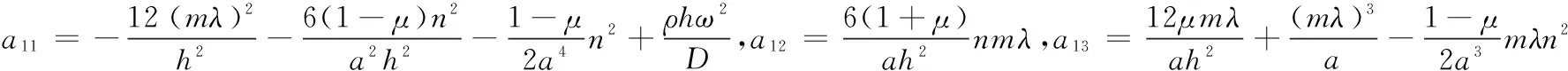
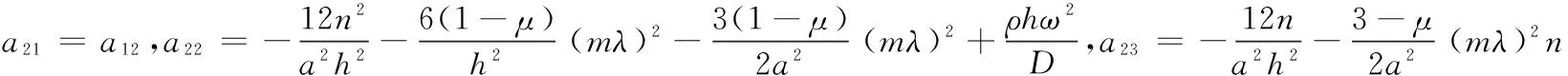
附錄D

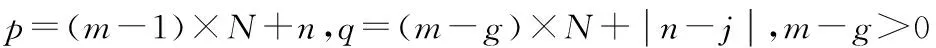
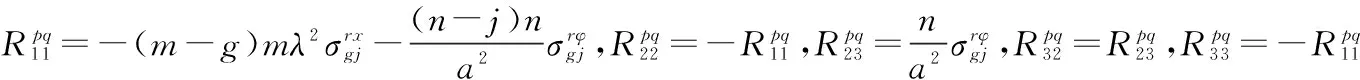
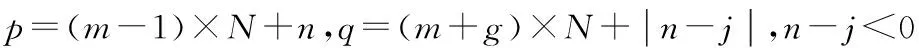
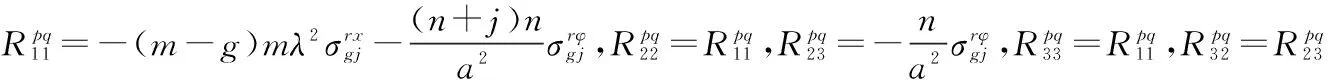
Natural frequencies of underwater complex stress structures

YANG Nian1, CHEN Luyun1, YI Hong1, LIU Yong2

(1. State Key Laboratory of Ocean Engineering, Shanghai JiaoTong University, Shanghai 200240, China;2. Ship Scientific Research Center of China, Shanghai Branch, Shanghai 200011, China)

The influence of the complex stress in underwater structure on its natural frequency was discussed and the limitation of the assumption of overall uniform stress distribution in former studies was revealed: the stresses in underwater structures are often very complex because of their working environment. The coaction of complex stress and fluid-structure coupling offers a nonlinear eigenvalue problem which is difficult to solve. An underwater cylindrical shell was taken as an example and based on the Flügge shell theory, considering the fluid-structure interaction and making use of the orthogonality of specific order modes, the dynamic equation of the structure was derived. The stress-caused coupled fluid structure modes were calculated by means of the polynomial approximation and quadratic matrix linearization. In the case study, the natural frequencies of structures with different types of stresses were calculated and the influence characteristics of different types of stresses were analysed and compared.

complex stress; fluid-structure interaction; structure vibration; natural frequency

2015-05-07 修改稿收到日期：2015-10-26

楊念 男，博士生，1989年3月生

易宏 男，教授,博士生導師，1962年5月生

TB535

A

10.13465/j.cnki.jvs.2016.22.015