基于Newmark-β法的載荷識別研究

蘇文獻,范正煉，鄧 蕾,陳 功

(1.上海理工大學能源與動力工程學院,上海 200093; 2.上海市質量監督檢驗技術研究院,上海 201114)

?

基于Newmark-β法的載荷識別研究

蘇文獻1,范正煉1，鄧 蕾1,陳 功2

(1.上海理工大學能源與動力工程學院,上海 200093; 2.上海市質量監督檢驗技術研究院,上海 201114)

基于已有的Newmark-β法正反分析原理,研究了單根換熱管振動的載荷識別,并且在對單根換熱管進行識別時探討了響應選取、時間步長、響應測量點等參數對識別結果的影響.

Newmark-β; 反分析原理; 載荷識別

動載荷識別技術在很多工程領域已經得到了較為廣泛的研究和應用[1-2],尤其它對減震、隔震、抗震的設計以及機械結構的故障診斷等方面可以提供不錯的服務,是這些領域優化設計中的非常重要的參考因素.在換熱管束的振動方面,國內外一些學者利用振動試驗以及理論方法對折流板與換熱器管束之間的沖擊載荷進行了識別,提出了諸如盲解卷積法[3]、橫向波技術[4-6]等方法.本文將采用時域內Newmark-β法對換熱器的單根換熱管進行載荷識別的研究,并分別討論動力響應、時間步長以及響應測量點的選取對載荷識別結果的影響.

1 Newmark-β法反分析原理

由Newmark-β法正分析原理可知,第(t+Δt)時刻的位移響應可以通過已知的載荷由式(1)求解得到

(1)

(2)

(3)

根據動載荷識別的線性假設,我們可以將式(1)改寫為

(4)

(5)

式中:u′t+Δt和u″t+Δt是ut+Δt的兩個分量,有以下的關系:

(6)

(7)

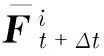
(8)

將式(8)代入式(4),可得:

(9)

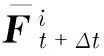
(10)

當我們經過測量已經知曉了m個測點的振動響應,可以是位移值、速度值以及加速度值中的一種或者多種,下面對不同的響應作分別的探討.

(11)

(12)

式(12)又可以改寫成:

(13)

其中:

(14)

以上的是在已知測點的位移響應時來計算結構載荷的方法,依照上面的方法,同理也可以通過速度或者加速度響應來計算結構載荷.

(2) 若已測得的響應為速度響應時,則設:

(15)

整理后可得到:

(16)

(3) 同理,若以加速度為振動的已測響應來識別振動載荷時,則可設:

(17)

與速度響應識別的情況類似,最后整理可得:

(18)

2 單根換熱管的載荷識別

計算模型如圖1所示,長為4 m的換熱管,兩端為固支約束,在MATLAB軟件中建立其有限元計算模型,共分為29個單元,30個節點,60個自由度,分別在第7,15,23號點上施加簡諧激勵.

具體參數如表1所示.

圖1 計算模型Fig.1 Computational model表1 設計參數Tab.1 Design parameters

換熱管長度l/m換熱管外徑Do/m換熱管內徑Di/m彈性模量E/Pa泊松比μ密度ρ/(kg·m-3)40.0250.0212×10110.37800

通過計算得到的模型的各個節點的位移響應、速度響應、加速度響應分別如圖2—4所示.

圖2 各個節點位移響應圖Fig.2 Displacement response of each node

圖3 各個節點的速度響應圖Fig.3 Velocity response of each node

2.1 不同的響應選取對載荷識別結果的影響

選取時間步長Δt = 0.01 s,激勵作用時間為1 s,選取正分析計算而得的第10,18,25節點的位移響應以及速度響應進行載荷識別,并分別對其添加5%,10%的高斯白噪聲,討論兩種響應識別方法的抗干擾性能.為了能夠更直觀地表現出兩種響應進行識別時結果的區別,選用文獻[7]中的誤差水平估計方法對結果進行誤差統計,結果如圖5所示.

圖4 各個節點的加速度響應圖Fig.4 Accelerate response of each node

圖5 兩種不同響應識別方法識別結果 的誤差水平估計圖Fig.5 Estimation of error level of identification result under two different response identification method

從圖5中,可以發現以速度響應對載荷進行識別時的結果要優于以位移響應進行載荷識別的結果,并且以速度響應進行識別時的結果對于外界的干擾的影響也小于位移響應.

2.2 識別位置對載荷識別結果的影響

分別選取第7,9節點,第14,16節點,第21,22節點3組的速度響應作為測量響應,對第15,23節點的載荷進行識別,其誤差水平估計如表2所示.

為了更直觀,將不同測量點組的誤差水平估計繪于一圖,如圖6所示,在眾多的測量點組當中,第15節點在以第14,16點為測量點時的識別結果較其他兩組要好,而第23節點則以第21,22節點為測量點時的識別結果最好.另外可以發現的是,選取靠近待識別點的點為測量點的識別結果要好于遠離待識別點的測量點的識別結果.這一結果與文獻[8],[9]的結果相類似,表明了越接近載荷施加點位置處的響應越能夠反應出施加載荷的信息,識別結果要更加的理想.

表2 不同測量點組的識別結果誤差評估水平%

圖6 不同測量點組的識別結果誤差水平估計Fig.6 Estimation of error level of identification result underf different measurement points

2.3 時間步長對載荷識別結果的影響

以第14,16節點的速度響應作為一組測量點,對第15節點處的載荷進行識別,分別選取不同的時間步長,其誤差水平估計如圖7所示.

圖7 不同時間步長下識別結果的誤差水平估計Fif.7 Estimation of error lecel of identificaiton result under different time steps

可以發現,由于Newmark-β法為逐步積分的方法一種,會因為不斷地迭代而產生一定的累積誤差.當時間步長選取過大時,會造成載荷識別信息的不完整,而當時間步長選得過小時,則會造成識別的載荷結果出現較大的誤差,該現象與文獻[10]中使用Wilson法進行識別時得到的結論相類似,所以對于每一種載荷識別的工況,都應該選取一個最佳的時間步長,以得到最精確的識別結果.

3 分析與討論

通過幾個算例的分析,首先比較了Newmark-β反分析原理識別載荷時選取不同的響應,即位移響應和速度響應進行載荷識別時的區別,結果表明以速度響應作為已測的響應進行識別時的結果無論是在有無外界干擾的情況下都要優于以位移響應進行識別的結果,但是對于較高的高斯白噪聲干擾,其識別的結果并不很理想.

此外,分別選取了3組不同的響應測量點進行載荷識別,結果表明:測量點的選取應該要靠近待識別的載荷點處,可以更多地體現所加載荷的信息.

最后,Newmark-β法是一種逐步積分的數值方法,所以就識別的時間步長對識別結果的影響作了探討,結果表明:過大的時間步長會造成載荷識別結果信息的缺失,并不能夠得到理想的曲線,然而當時間步長選得過小時,也可發現識別的結果開始出現較大誤差,并且這一誤差隨著時間步長的進一步減小會變得更大,所以在用Newmark-β法進行識別時,應當就每一種工況的載荷識別的時間步長進行選取.

[1] 張玉娥,白寶鴻.地鐵列車振動對隧道結構激振荷載的模擬[J].振動與沖擊,2000,19(3):68-71.

ZHANG Yue,BAI Baohong.The method of identifying train vibration load action on subway tunnel structure [J].Journal of Vibration and Shock,2000,19(3):68-71.

[2] 蓋曉男.高速飛行器動載荷識別研究[D].哈爾濱:哈爾濱工業大學,2013.

GAI Xiaonan.Research on identification of dynamic load of high speed vehicle[D].Harbin:Harbin Institute of Technology,2013.

[3] ANTUNES J,PAULINO M,IZQUIERDO P.Blind identification of impact forces from multiple remote vibratory measure ments[J].International Journal of Nonlinear Sciences and Numerical Simulation,2001,2(1):1-20.

[4] DEARAUJO M,ANTUNES J,PITEAUITEAU P.Remote identification of impact forces on loosely supported tubes:Part 1:basic theory and experiments[J].Journal of Sound and Vibration,1998,215(5):1015-1041.

[5] ANTUNES J,PAULINO M,PITEAU P.Remote identification of impact forces on loosely supported tubes:Part 2—Complex vibro-impact motions[J].Journal of sound and vibration,1998,215(5):1043-1064.

[6] PAULINO M,ANTUNES J,IZQUIERDO P.Remote identification of impact forces on loosely supported tubes:Analysis of multi-supported systems[J].Journal of Pressure Vessel Technology,1999,121(1):61-70.

[7] 金輝,徐菁,張方,等.Wilson-θ 反分析法的動載荷識別精度的若干問題[J].振動.測試與診斷,2013,33(5):782-788.

JIANG Jinhui,XU Jing,ZHANG Fang,et al.Wilson-θ dynamic load identification accuracy problems of inverse analysis method [J].Journal of Vibration,Measurement & Diagnosis,2013,33(5):782-788.

[8] 毛玉明.動載荷反演問題時域分析理論方法和實驗研究[D].大連:大連理工大學,2010.

MAO Yuming.The theoretical approach and experimental study on the inverse problem of dynamic force identificat-ion in time domain[D].Dalian:Dalian University of Tech-nology,2010.

[9] GUO X L,LI D S.Experiment study of structural random loading identification by the inverse pseudo excitation method[J].Structural Engineering and Mechanics,2004,18(6):791-806.

[10] 陳英華.動載荷時域 Wilson-θ 識別方法和 PATRAN 二次開發[D].南京:南京航空航天大學,2010.

CHEN Yinghua.Dynamic load identification Wilson-θ method in time domain and PATRAN secondary development [D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010.

Newmark-β-based loading identification

SU Wen-xian1,FAN Zheng-lian1,DENG Lei1,CHEN Gong2

(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;2.Shanghai Institute of Quality Inspection and Technical Research,Shanghai 201114,China)

Based on the forward and inverse Newmark-β analysis principles,the loading identification on the single heat exchange tube is conducted.Accordingly,the impacts of response selection,time step and response measurement point on identification results are investigated.

Newmark-β; inverse analysis principle; loading identification

蘇文獻(1967-),男,博士,副教授.E-mail:775463083@qq.com

TH 49

A

1672-5581(2016)02-0142-05