基于Matlab的三種圖像去噪方法的比較研究*

賽地瓦爾地·買買提，艾尼瓦爾·肉孜

（喀什大學 物理與電氣工程學院，新疆 喀什 844006）

基于Matlab的三種圖像去噪方法的比較研究*

賽地瓦爾地·買買提，艾尼瓦爾·肉孜

（喀什大學 物理與電氣工程學院，新疆 喀什 844006）

為了研究各種去噪算法的優劣，在介紹圖像去噪的基本原理和方法的基礎上，采用傳統的線性、非線性以及頻域的方法，對數字圖像進行去噪效果的分析比較和仿真實現。運用Matlab仿真平臺的驗證結果表明：中值濾波對椒鹽噪聲的去噪效果很好；維納濾波對高斯噪聲有一定的降噪效果，且較好地保護了圖像的邊緣細節信息和高頻細節信息；三維塊匹配（BM3D）方法相對于以上幾種方式來說，對圖像降噪效果最好，對圖像有著明顯的平滑效果，且由于充分使用了各模塊之間的關系，使得信噪比較高。

圖像去噪；中值濾波；維納濾波；三維塊匹配法（BM3D）；平均結構相似度

0 引 言

在傳播過程中，圖像一般都會被各種各樣的噪聲污染。因為噪聲是一個隨機變化的信號，所以通常利用概率統計方法來進行分析。圖像中的噪聲可以看作是圖像的顏色及亮度信息在傳輸過程中隨機變化的結果，通常是電子噪聲的一個方面。此外，圖像的捕捉也會引入許多雜散的外部信息，從而增加圖像受噪聲污染的程度。所以，為使圖像在后續處理時的準確度和清晰度能達到一個好的效果，必須在處理即圖像分割、特征提取、邊緣檢測、模式識別等之前，對現有的圖像進行去噪[1]。它不僅是一切圖像處理的前提，也是圖像處理中極為重要的步驟，極具意義。

1 中值濾波及仿真分析

中值濾波是一種非線性濾波方式。該方式的優點是不需要利用圖像的統計特性，因此較為簡便。該濾波的主要思維是，在一個領域中，使用一個像素點臨近鄰域內的所有像素值的中值，代替這個像素點的像素值[2-3]。

一個一維序列f1,…,fn，取窗口長度為奇數m，從該序列中相繼抽出m個數，依次排列為fi-v,…,fi-1,…,f1,…fi+1,…,fi+v，其中i為所用窗口序列的中心位置。然后，再將上述序列按照數值從小到大的順序進行排列。最后，在排好大小的序列中取出中心的數，即：

例如，對于一個序列{1，5，9，2，7}，通過中值濾波器重新排列后得到的新序列為：{1，2，5，7，9}，中間值為5。

基于上述的中值濾波方法，選取如圖1所示的圖像作為實驗的原始圖像，并依次給圖像加入均值為0，方差為0.03的高斯噪聲和噪聲密度為0.03的椒鹽噪聲，相關的仿真結果分別如圖1～圖8所示。

圖1 原始圖像(313×330)

圖2 含椒鹽噪聲圖像(SSIM=0.73)

圖3 中值濾波降噪(SSIM=0.98)

圖4 中值濾波降噪(SSIM=0.96)

圖5 原始圖像(313×330)

圖6 含高斯噪聲圖像(SSIM=0.34)

圖7 中值濾波降噪(SSIM=0.74)

圖8 中值濾波降噪(SSIM=0.87)

由上述仿真結果可知，被椒鹽噪聲污染的圖像（見圖2）經過中值濾波后，圖像中的噪聲幾乎全部被濾除（見圖3、圖4），但對高斯噪聲幾乎沒有效果（見圖7、圖8）；平均結構相似度SSIM的變化越大，表明降噪效果越好，如圖3、圖4所示；中值濾波的去噪效果與采用窗口成正比（對高斯噪聲來說）。窗口尺寸越大，圖像降噪效果越好，但代價是圖像的模糊程度越大，如圖7、圖8所示。

2 維納經驗濾波及仿真分析

使用維納濾波方法的目的是得到信號以及噪聲的譜密度信息，以及能夠通過一個線性時不變系統使輸出信號與原始信號盡量相似[4-5]。假設原始信號以及噪聲信號是加性關系，則令s(t)是原始信號，

n(t)是噪聲信號，?( t)作為輸出信號，g(t)作為濾波器的系統函數，則四者的關系可以描述如下：

令誤差函數為：

式中，α是濾波器的延遲。

由式（2）可以推出：

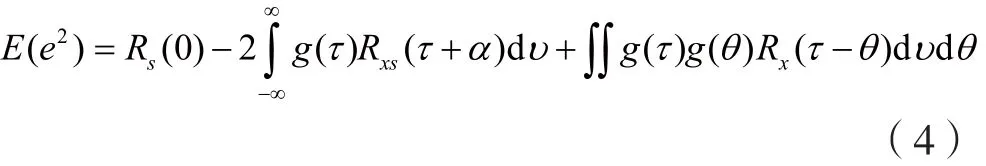
式中，x(t)=s(t)+n(t)，Rs是s(t)的自相關函數，Rxs是x(t)與s(t)的互相關函數。如果x(t)與s(t)不相關，則有Rs=Rxs且Rx=Rs+Rn。

濾波器的目的是使E(e2)得到最小值，故應先求得E(e2)的一階增量：

要想取得最小值，只要使

式（5）即為維納濾波器的基本理論等式。

離散序列的有限沖擊響應維納濾波器，其框圖如圖9所示。

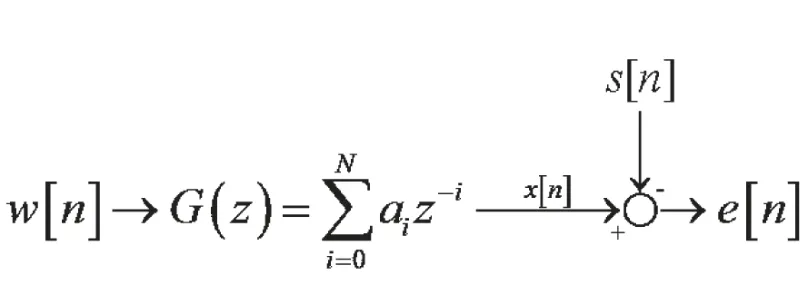
圖9 維納濾波器

對于這個FIR維納濾波器，可以得到x[n]的表達式為：

根據框圖，又可以定義出e[n]=x[n]-s[n]。由于濾波器的目的是使E(e2)得到最小值，所以有：

由e[n]=x[n]-s[n]可以得出：

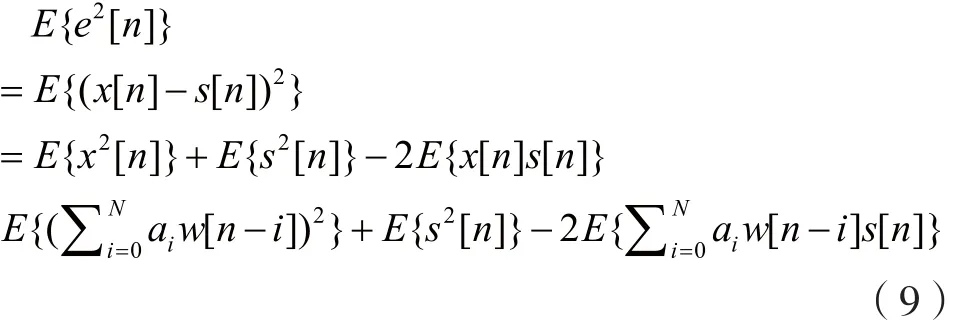
為了得出向量[a0,…,aN]，必然使E{e2[n]}取得最小值，即：

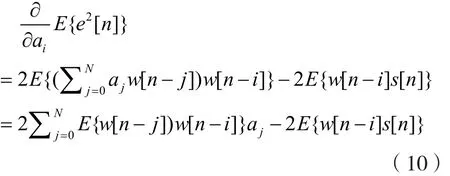
式中，i=0,…N。

假定s[n]與w[n]是不變化的，則由自相關函數Rw[m]與互相關函數Rws[m]的定義出發，可以將式（10）改寫為：

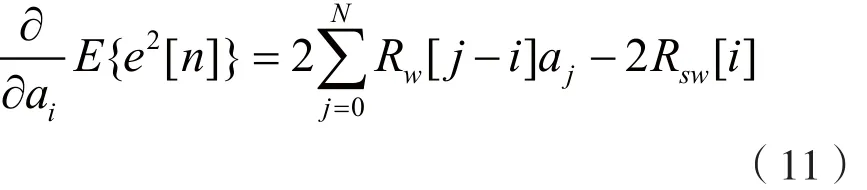
式中，i=0,…N。

為取得最小值，令：

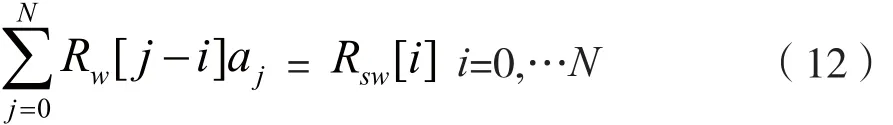
將式（12）寫成矩陣形式，可以得到：

這個矩陣又被稱為維納-霍夫等式。

基于上述的維納濾波方法，選取如圖10所示的圖像作為實驗的原始圖像，并依次給圖像加入均值為0，方差為0.03的高斯噪聲和噪聲密度為0.03的椒鹽噪聲，相關的仿真結果分別如圖11～圖15所示。

圖10 原始圖像(313×330)

圖11 含高斯噪聲(SSIM=0.35)

圖12 維納濾波降噪結果(SSIM=0.76)

圖13 原始圖像 (313×330)

圖14 含椒鹽噪聲(SSIM=0.75)

圖15 維納濾波降噪結果(SSIM=0.79)

由圖11、圖12對比可知，維納濾波對高斯噪聲有一定的降噪效果，且較好地保護了圖像的邊緣細節信息和高頻細節信息。相比實驗前后的SSIM值可以看出（見圖14、圖15），維納濾波器對椒鹽噪聲幾乎沒有降噪效果。

3 BM3D及仿真分析

三維塊匹配方法是一種常用的非局部估計方法。在這個算法中，圖像像素點值通過一個與以該像素點為中心的區域相似的另外一個區域來進行估計。主要步驟：首次，將目標圖像分成一定大小的小塊圖片；其次，按照圖像塊之間的相似性，把互相相似的二維圖像塊合并成一個三維數組；再次，使用聯合濾波方法對這些三維數組進行處理；最后，對這些三維數組進行逆變換，返回到原始圖像，從而得到降噪后圖像。該方法的降噪效果較好，不僅可以得到一個理想的較高信噪比，而且視覺效果也很不錯[6-7]。

3.1 基于小波收縮變換的初步三維塊匹配算法

對基于小波收縮變換的三維塊匹配算法理論作簡單推導。

首先，仍然給出與上文形式一樣的帶噪圖像模型：z(x)=y(x)+η(x)。這里說明，噪聲η(x)為方差σ2的高斯噪聲，即η(x)～N(0,σ2)。定義Zx為從圖像z中選取的大小為N1×N1的板塊，y?為最終得到的處理后的圖像。為了能夠給后續工程提供模版，將當前正在處理的板塊稱作ZxR，即為一個參考模塊。

塊匹配方法是要尋找到一個與參考模塊ZxR極為相似的模塊。因為這種尋找方式的精確度受噪聲影響，因此這里將利用板塊相似的手段，從而在二維變換域中進行粗糙降噪。

定義板塊距離（與相似度成反比例）：

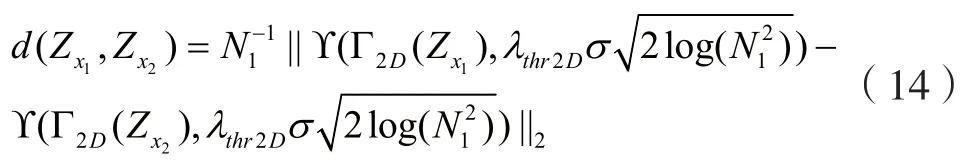
式中，x1，x2∈X，Γ2D是一個二維的線性變換方法（如DCT、DFT等），Υ是硬閾值處理方法，λthr2D指固定的閾值參數，‖·‖2指平方模。通常情況下，Υ定義為：

塊匹配的結果是一個集合SxR，集合中的板塊坐標由式（15)可以與相似。因此，定義SxR：

式中，τmatch是兩塊板塊能夠被認為相似的最大距離。

對于已經得到相似板塊的集合SxR，將其與原來的板塊堆積成一個形式為N1×N1×|SxR|的三維數組，然后對使用三維聯合變換Γ3D，以得到無噪聲信號的稀疏表示。隨后，再用逆變換重建估計：

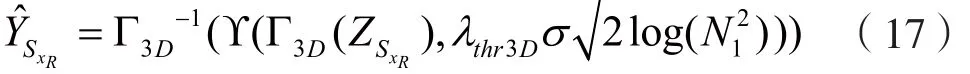
式中，λthr3D是固定閾值參數。數組包含了以及圖像板塊的正確的估計板塊

定義這些局部估計量的權重為：

式中，Nhar是經過硬閾值后非零變換系數的個數。

觀察可以得出，σ2Nhar的值與的方差值相等。因此，的稀疏分解可以得到噪聲最小的估計圖像。

3.2 BM3D濾波器最終估計法

可以構建一個維納經驗濾波器作為上述閾值算法的最終估計法。令Ex為x上的一個大小為N1×N1的板塊。為了提高塊匹配方式的準確性，用兩個板塊間相減的方式替代上一小節式（17）來定義SxR：

接下來，使用線性維納濾波器來代替硬閾值算法。作為三維變換域的算法，維納濾波器的衰減系數為：

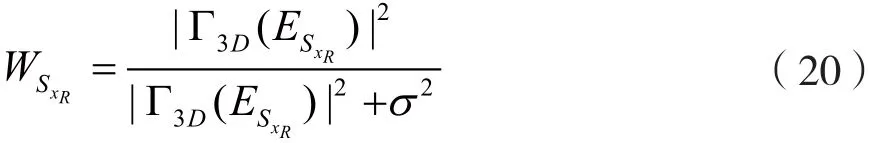
通過衰減系數給出的圖像估計為：

最后，對于有重疊的板塊，通過加權求和取平均的方式得到真實的圖像估計。其中，加權系數ωxR為：

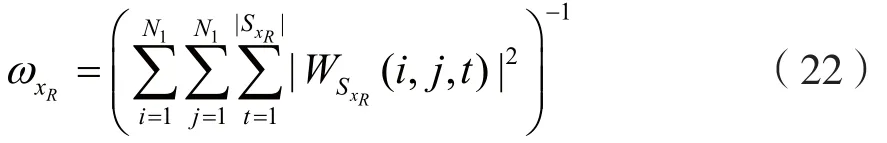
3.3 BM3D算法法則總結

令將要處理的帶噪聲的圖像大小為M×N，即|X|=MN。利用兩個同等大小的緩沖區：ebuff（估計值緩沖區）以及wbuff（權重值緩沖區）來表示算式中的分子和分母。ebuff(x)表示坐標x處的像素值，而ebuffx則表示x處的一個板塊。

于是，BM3D算法可以大致分為如下幾步：

（1）初始化：對于所有的x∈X，令ebuff(x)=0且wbuff(x)=0。

（2）局部硬閾值估計：

對于每個xR：

①塊匹配：由式（16）計算SxR的值，并限制搜索范圍為以xR為中心的Ns×Ns的區域。如果|SxR|＞N2（N2為SxR內所允許的最大板塊個數），那么保留距離值較小的板塊，其他的則舍棄。

得出估計緩沖區的值：

相應地，有：

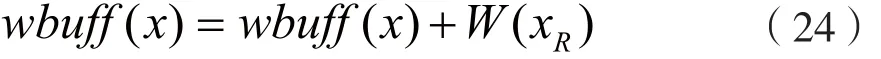
（4）局部維納估計：將上述的e(x)作為初始估計量，并重置ebuff(x)=0、wbuff(x)=0。

對于每個xR：

①塊匹配：由式（19）計算SxR的值，并限制搜索范圍為以xR為中心的Ns×Ns的區域。如果|SxR|＞N2（N2為SxR內所允許的最大模塊個數），那么保留與ExR距離值較小的板塊，其他的則舍棄。

相應的，wbuff( x)=wbuff( x)+W( xR)。

仿真結果及結論，如圖16～圖18所示。

由仿真結果可知，峰值信號信噪比PSNR越大，表明降噪效果越好（對比圖16和圖18所得）。

圖16 原始圖像

圖17 含高斯噪聲(PSNR=19.45,σ=30)

圖18 BM3D降噪結果 (PSNR=30.64,σ=30)

綜上，BM3D方法相對于以上幾種方式來說，是圖像降噪效果最好的方法。它使用塊匹配的方式對圖像平滑效果明顯，且由于充分使用了各個模塊間的關系，使得信噪比較高。總的來說，BM3D圖像降噪方法是一種較為優秀的圖像降噪方法。

4 結 語

基于圖像去噪的基本原理和方法，運用Matlab仿真平臺，對數字圖像進行去噪效果的分析比較和仿真實現。仿真結果表明：中值濾波對圖像的椒鹽噪聲非常有效，但對高斯噪聲幾乎沒有效果；維納濾波對高斯噪聲有一定的降噪效果，且較好地保護了圖像的邊緣細節信息和高頻細節信息；BM3D方法相對于以上幾種方式來說，噪聲圖像的峰值信號的信噪比PSNR相比去噪后圖像的峰值信號的信噪比PSNR明顯變高，是圖像降噪效果最好的方法。同時，它使用塊匹配的方式對平滑效果明顯，且由于充分使用了各個模塊間的關系，使得信噪比較高。總的來說，BM3D圖像降噪方法是一種較為優秀的圖像降噪方法。

[1] 岡薩雷斯.數字圖像處理[M].第2版.北京:電子工業出版社,2003. Gonzales.Digital Image Processing[M].Second Edition.Beijing:Publishing House of Electronics Industry,2003.

[2] Hwang H,Haddad R.A.Adaptive Median Filters:New Algorithms and Results[J].IEEE Transactions on Image Processing,1995,4(04):499-502.

[3] 楊卓東,張欣,張濤等.改進自適應中值濾波的圖像去噪[J].通信技術,2015,48(11):1257-1260. YANG Zhuo-dong,ZHANG Xin,ZHANG Tao,et al.An Improved Adaptive Median Filter for Image Denoising[J]. Communication Technology,2015,48(11):1257-1260.

[4] Wiener N.Extrapolation,Interpolation,and Smoothing of Stationary Time Series[M].New York:Technology Press of the Massachusetts Institute,1949.

[5] Portilla J,Strela V,Wainwright M,Simoncelli EP.Image Denoising Using Scale Mixtures of Gaussians in the Wavelet Domain[J].IEEE Transactions on Image Process ing,2003,12(11):1338-1351.

[6] Zhou D,Cheng W.Image Denoising With An Optimal Threshold and Neighboring Window[J].Pattern Recognition Letters,2008,29(11):1694-1697.

[7] Malfait M,Roose D.Wavelet-based Image Denoising Using A Markov Random Field A Priori Model[J].IEEE Transactions on Image Processing,1997,6(04):549-565.

賽地瓦爾地·買買提（1985—），男，碩士，助教，主要研究方向為信號與信息處理、圖像處理；

艾尼瓦爾·肉孜（1960—），男，本科，教授，碩士生導師，主要研究方向為信號中的噪聲效應研究。

Comparison of Three Image De-Noising Methods based on Matlab

SAIDIWAERDI·Maimaiti, AINIWAER·Ruozi
(College of Physics and Electrical Engineering, Ka Shi University, Kashi Xinjiang 844006,China)

In order to evaluate the quality of de-noising algorithms, the principles and methods for eliminating image noise are described.Traditional methods such as inlinear，nonlinear and frequency domains, are used to eliminate image noise, and their results eliminating image are analyzed and compared. Simulation with Matlab indicates that the median filtering is very good in denoising of salt and pepper noise, and Wiener filtering fairly good in denoising of Gaussian noise and better protection of Edge details and high-frequency details for image. Three-dimensional block matching (BM3D)method, as compared with the above methods, is much better for image noise reduction, has more Significant smoothing effect on the image and for its full use of the relationship of between various modules, even higher SNR for noisy image.

image denosing; median filtering; wiener filtering; BM3D;SSIM

National Natural Science Foundation of China(No.21363010)

TP308

A

1002-0802(2016)-07-0856-06

10.3969/j.issn.1002-0802.2016.07.012

2016-03-23;

2016-06-20 Received date:2016-03-23;Revised date:2016-06-20

國家自然科學基金（No.21363010）