基于代數(shù)和的Gold序列相關(guān)性分析及擴頻同步應(yīng)用*

張 野

（92124部隊，遼寧 大連 116023）

基于代數(shù)和的Gold序列相關(guān)性分析及擴頻同步應(yīng)用*

張 野

（92124部隊，遼寧 大連 116023）

并行組合擴頻系統(tǒng)相比直接擴頻通信傳輸效率更高，能更好地應(yīng)用于海上復(fù)雜環(huán)境無線通信。應(yīng)用序列代數(shù)和的概念，對零相位差處Gold序列良好的代數(shù)和相關(guān)性進行分析，進一步討論非零相位差處Gold序列代數(shù)和相關(guān)的多值特性。針對Gold序列良好的代數(shù)和相關(guān)特性，并行組合擴頻系統(tǒng)在序列非同步情況下建立仿真模型，結(jié)果表明Gold序列集可實現(xiàn)并行組合擴頻系統(tǒng)的序列自同步。

Gold序列；相關(guān)性；并行組合擴頻系統(tǒng)；序列同步

0 引 言

擴頻通信具有很強的抗窄帶干擾和多徑干擾能力，同時能夠有效抵御截獲，加強無線通信中的保密性，在軍民海上衛(wèi)星及微波通信系統(tǒng)中得到了廣泛應(yīng)用。但是，直接擴頻系統(tǒng)與并行組合擴頻技術(shù)相比，傳輸效率較低。因此，并行組合擴頻技術(shù)受到很多學(xué)者專家的關(guān)注。研究主要集中在并行組合擴頻和其他技術(shù)的結(jié)合[1]、并行組合擴頻技術(shù)的調(diào)制[2]、并行組合擴頻在不同通信環(huán)境中的應(yīng)用[3]等方面。區(qū)別于直接序列擴頻系統(tǒng)傳輸?shù)膯我粩U頻序列，并行組合擴頻系統(tǒng)傳輸?shù)氖遣⑿薪M合序列。組合偽隨機序列是并行組合擴頻技術(shù)的核心組成，尋找和構(gòu)造滿足需求的偽隨機序列是工程應(yīng)用中的關(guān)鍵問題。Gold序列以其數(shù)量大、統(tǒng)計特性良好等優(yōu)點，在各種擴頻技術(shù)中被廣泛研究及應(yīng)用[4]。作為經(jīng)典偽隨機序列，組合Gold序列相關(guān)性的研究對其在并行組合擴頻技術(shù)中的應(yīng)用有著重要的意義。本文采用序列代數(shù)和的概念對Gold序列進行分析，為并行組合擴頻技x術(shù)中序列同步提供了良好的理論基礎(chǔ)，并將其在系統(tǒng)中進行了同步仿真，驗證了Gold序列在非同步并行組合擴頻系統(tǒng)中具有良好的可靠性。

1 Gold序列的相關(guān)特性

Gold序列是m序列優(yōu)選對相加取模2值得出[5]。Gold序列在零時延處的自相關(guān)和互相關(guān)值分別為N和-1。其中，N為偽隨機序列周期長度。非零相位差處Gold序列的互相關(guān)系數(shù)和自相關(guān)系數(shù)均取三個值，為[6-7]：

由此可知，當(dāng)在非零相位差處Gold序列的互相關(guān)系數(shù)n取值較大時，其自相關(guān)系數(shù)和互相關(guān)系數(shù)取值較小，且其值隨著n的增大而減小。

2 代數(shù)和相關(guān)性的概念

文獻[8]針對并行組合擴頻系統(tǒng)中組合序列并行傳輸?shù)奶攸c，提出了代數(shù)和序列相關(guān)性的概念。在并行組合擴頻系統(tǒng)中應(yīng)用代數(shù)和序列相關(guān)性分析序列相關(guān)性更準確，可以為接收端序列解擴、序列間互干擾以及序列自同步提供良好的理論基礎(chǔ)。

擴頻序列集由序列{A1}、{A2}…{Al}…{AM}組成。設(shè)序列周期長度為N，{Al}中的第i個碼元為ail（其中1≤i≤N,1≤l≤M），則從序列集中取r條序列，并乘以權(quán)系數(shù)ql后疊加生成序列{B}。序列{B}中第i個碼元為bi：

式中，權(quán)系數(shù)ql∈{+1,0,-1}用于控制序列的極性。若{B}中序列由{Al}和其他序列疊加生成，則{Al}和{B}兩序列的代數(shù)和自相關(guān)函數(shù)為：

序列{Al}和{B}的代數(shù)和自相關(guān)系數(shù)定義為：

若{B}中序列不是由{Al}序列參與疊加生成，則{Al}和{B}兩序列的代數(shù)和互相關(guān)函數(shù)及互相關(guān)系數(shù)也由式(4)和式(5)表示。

組合序列{B}和序列{Al}的代數(shù)和自相關(guān)函數(shù)實際上是{Al}的自相關(guān)函數(shù)以及{Al}與其他參與構(gòu)成{B}的序列互相關(guān)函數(shù)的加權(quán)和，權(quán)系數(shù)由參與構(gòu)成{B}的序列的r個極性選取因子確定。

由偽隨機序列的相關(guān)性可以推知以下組合序列的代數(shù)和相關(guān)性：

（1）若序列集中各序列自相關(guān)特性良好，且彼此正交，則代數(shù)和自相關(guān)系數(shù)在零相位差處為1。

（2）若序列集中序列彼此正交，則組合序列與集內(nèi)不參與構(gòu)成組合序列的其他序列的代數(shù)和互相關(guān)系數(shù)在零延時處必為0，而與組合序列的構(gòu)成序列個數(shù)r無關(guān)。即若在并行組合擴頻系統(tǒng)中使用正交序列集進行擴頻，則發(fā)送端映射后得到的組合序列和其他序列仍存在正交性。

組合序列的代數(shù)和相關(guān)特性是依據(jù)參與構(gòu)成的序列加權(quán)系數(shù)及其序列自有相關(guān)特性求得的，所以在一定程度上，組合序列的代數(shù)和相關(guān)特性繼承了各參與構(gòu)成序列的相關(guān)特性。但是，單一序列的相關(guān)性僅能定性分析組合序列的相關(guān)性，而組合序列的相關(guān)性可由代數(shù)和相關(guān)性來進行定量計算。所以，關(guān)于代數(shù)和相關(guān)特性在并行組合擴頻系統(tǒng)中的研究十分必要。

3 Gold序列的代數(shù)和相關(guān)性

若組合序列{B}由r條Gold序列加權(quán)求和后得到，其中m條序列的權(quán)系數(shù)qm取值為1，(r-m)條序列的權(quán)系數(shù)qm取值為-1。零時延處，Gold序列代數(shù)和自相關(guān)函數(shù)為：

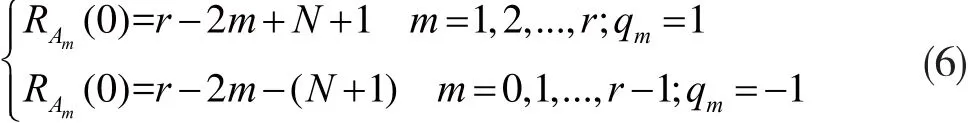
而序列{B}與序列集內(nèi)其余Gold序列的代數(shù)和互相關(guān)函數(shù)可表示為：

式中，m=0,1,…,r。

可求(6)的極值，并取其絕對值，則其代數(shù)和自相關(guān)系數(shù)最大值取值范圍為：

Gold序列自相關(guān)和互相關(guān)系數(shù)取三種不同值，故其代數(shù)和相關(guān)系數(shù)應(yīng)取多值，則其自相關(guān)旁瓣峰值可表示為：

對組合序列而言，若某時延處參與組成的r條序列的自相關(guān)系數(shù)同時出現(xiàn)旁瓣峰值，則序列{B}的代數(shù)和自相關(guān)旁瓣系數(shù)取峰值應(yīng)為但此種情況并不確定出現(xiàn)。

取7條Gold序列{A1}、{A2}、…、{A7}定量分析。設(shè)N=127，r=3的組合序列{B}由{A1}、{A2}、{A3}疊加得到，3條序列極性權(quán)系數(shù)設(shè)為1，則B(j)=A1(j)+A2(j)+A3(j)，(j=0,1,…,N-1)。圖1為序列{A1}、{A2}、{A3}與序列{B}的代數(shù)和自相關(guān)系數(shù)。這里，采用時延相位差點數(shù)n作為橫坐標(biāo)，組合序列代數(shù)和相關(guān)系數(shù)ρ作為縱坐標(biāo)。

圖1 序列{A1}、{A2}、{A3}與{B}的代數(shù)和自相關(guān)系數(shù)

由圖1可以看出，零相位差處{A1}、{A2}、{A3}的代數(shù)和系數(shù)一致，均為滿足式(6)的推導(dǎo)；而非零時延處有較多旁瓣，且旁瓣呈多值特性，最大自相關(guān)旁瓣絕對值約為0.4。可見，組合序列代數(shù)和自相關(guān)性相對單一序列自相關(guān)性明顯下降。

圖2（a）、圖2（b）、圖2（c）和圖2（d）是序列{A4}、{A5}、…、{A7}與序列{B}的代數(shù)和互相關(guān)系數(shù)。

圖2 序列{A4}、{A5}、…、{A7}與{B}的代數(shù)和自相關(guān)系數(shù)

由圖2可見，零相位差處序列{A4}、{A5}、…、{A7}和序列{B}的4個代數(shù)和互相關(guān)系數(shù)取值是相同的，符合式(9)，可知零相位差處代數(shù)和互相關(guān)系數(shù)為則{A4}、{A5}、…、{A7}可近似認為和{B}正交。因Gold序列的自相關(guān)旁瓣與互相關(guān)最大取值相同，由式（10）得出可能的最大代數(shù)和互相關(guān)系數(shù)峰值這與圖2仿真中4個代數(shù)和互相關(guān)系數(shù)峰值絕對值均約為0.4相吻合。

可見，Gold序列代數(shù)和互相關(guān)系數(shù)也呈多值特性，存在多旁瓣峰值，組合序列代數(shù)和互自相關(guān)性較單一序列互自相關(guān)性下降，但相比其他種類序列，它的代數(shù)和相關(guān)性性能仍然具有優(yōu)越性。

4 Gold序列在并行組合擴頻系統(tǒng)中的應(yīng)用

在并行組合擴頻系統(tǒng)發(fā)射端將k比特信息進行串并轉(zhuǎn)換，并行送入數(shù)據(jù)-序列組合映射器。根據(jù)序列組合-數(shù)據(jù)映射算法，將r條不同序列從M條序列{PNi}(i=1,2,…,M)中選出，同時考慮序列的極性。取qi∈(1,-1,+1)，(i=1,2,…,M)，相應(yīng)碼片等幅度疊加形成多值組合序列：

式中，qi為序列極性，表示序列選取的控制因子。在映射時，若qi=±1，則與qi對應(yīng)的序列{PNi}可以被選取，且它的符號表示序列在選取時的正負極性；而qi=0時，與qi對應(yīng)的序列{PNi}則不會被選取。

在并擴系統(tǒng)中，每次發(fā)送的信息量k為：

在并行組合擴頻系統(tǒng)中，本地擴頻序列在接收端與接收序列進行相關(guān)解擴后，按照序列組合-數(shù)據(jù)逆映射算法，在M個相關(guān)器輸出值里面選出絕對值最大的r個，并結(jié)合其極性信息，最后經(jīng)過并串轉(zhuǎn)換還原發(fā)送的信息。

在并擴系統(tǒng)接收端，將組合序列與所有本地序列分別進行相關(guān)運算才能實現(xiàn)組合序列的捕獲，而正確捕獲要求序列組代數(shù)和相關(guān)系數(shù)具有零時延處尖銳的自相關(guān)值。根據(jù)Gold序列良好的代數(shù)和相關(guān)性，可將其應(yīng)用在并擴系統(tǒng)無噪情況中。圖3為擴頻序列總數(shù)M=16，r=2以及r=3時系統(tǒng)序列的捕獲概率；圖4為擴頻序列總數(shù)r=3，M=16以及M=32時的捕獲概率。其中，每個擴頻碼元采樣點為TC/2，TC為采樣周期。可以發(fā)現(xiàn)，在不同的信噪比Eb/N0條件下，無論r取何值，M越大則捕獲概率Pd越高；無論M取何值，r越大則捕獲概率Pd越高。

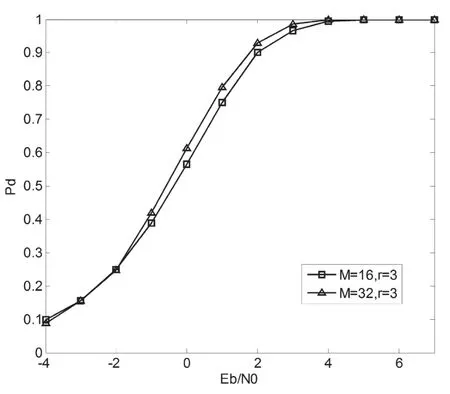
圖3 同r下選取發(fā)射的序列數(shù)M對捕獲概率的影響

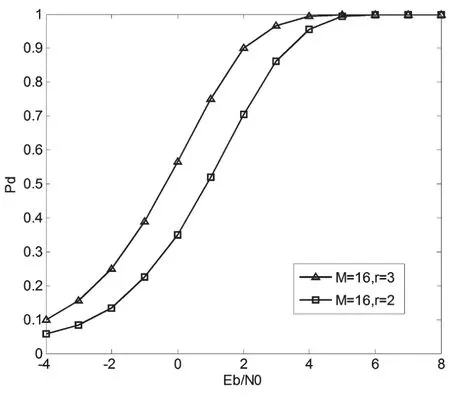
圖4 同M下選取發(fā)射的序列數(shù)r對捕獲概率的影響

5 結(jié) 語

本文對Gold序列的相關(guān)性以及代數(shù)和相關(guān)性進行了分析，針對Gold序列非零相位差處擁有良好相關(guān)性的特點，將Gold序列用于并行組合擴頻系統(tǒng)組合序列同步中，并在無噪聲情況下對序列同步的捕獲概率進行了仿真，驗證了Gold序列在非同步并行組合擴頻系統(tǒng)中應(yīng)用的可行性，同時得到結(jié)論：（1）組合序列捕獲概率和選取的擴頻序列數(shù)r成正比；（2）組合序列捕獲概率和系統(tǒng)擴頻序列總數(shù)M成正比。

[1] QI Lin,GUO Li-li,JIANG Xiao-fei.Performance Studies of UWB Communication System Based on Parallel Combinatory Spread Spectrum[C].International Conference on Wireless Communications,2009:1760-1763.

[2] 王 玫.短波并行組合擴頻通信系統(tǒng)關(guān)鍵技術(shù)的研究[D].哈爾濱:哈爾濱工程大學(xué),2009. WANG Mei.Study of Key Techniques for Shortwave PCSS Communication System[D].Harbin:Harbin Engineering University,2009.

[3] 殷敬偉,王蕾,張曉.并行組合擴頻技術(shù)在水聲通信中的應(yīng)用[J].哈爾濱工程大學(xué)學(xué)報,2010,31(07):958-962. YIN Jing-wei,WANG Lei,ZHANG Xiao.The Application of Parallel Combinatory Spread Spectrum in Underwater Acoustic Communication[J].Journal of Harbin Engineering University,2010,31(07):958-962.

[4] Yates K W,Beach M A,Copping A J.Binary Sequence With a High Crosscorrelation With Each Member of a Subset of Gold Codes[J].Electronics Letters,1986,22(18):930-932.

[5] 王玉東,劉春雷.Gold序列相關(guān)性的新證明及非最大Gold序列性質(zhì)研究[J].通信技術(shù),2014,47(03):241-246. WANG Yu-dong,LIU Chun-lei.A New Proof of Cross-Correlation Property of Gold Sequence and Non-Maximal Gold Sequence[J].Communications Technology,2014,47(03):241-246.

[6] 辛肖明,陳瓊.m序列優(yōu)選對及平衡Gold碼序列[J].北京理工大學(xué)學(xué)報,1990(S3):106-113. XIN Xiao-ming,Chen Qiong.Optimum m-Sequence Pairs and Blanced Gold Group[J].Journal of Beijing Institute of Technology,1990(S3):106-113.

[7] 黃劍明,施志勇,保錚.截短平衡Gold碼的統(tǒng)計特性分析[J].系統(tǒng)工程與電子技術(shù),2006(05):646-649. HUANG Jian-ming,SHI Zhi-yong,BAO Zheng. Analysis of the Statistic Characteristics of the Truncated Balance Gold Code[J].Systems Engineering and Electronics,2006(05):646-649.

[8] 姜曉斐.并行組合擴頻超寬帶通信系統(tǒng)的關(guān)鍵技術(shù)研究[D].哈爾濱:哈爾濱工程大學(xué),2012. JIANG Xiao-fei.Research on Key Technologies of UWB Communication Systems based on Parallel Combinatory Spread Spectrum[D].Harbin:Harbin Engineering University,2012.

Correlation and Application of Combinatory Gold Sequences in Spread Spectrum Synchronization

ZHANG Ye
(Troops 92124,Dalian Liaoning 116023,China)

As compared with direct sequence spread-spectrum communication,parallel combinatory spread spectrum system with high-efficient transmission , has a better application in marine wireless communication. According to the correlation properties of combinatory sequences, the correlation function at zero time delay of combinatory Gold sequences is analyzed, and the muti-peak value of correlation function at non-zero time delay is discussed. Aiming at the good correlation properties of combinatory Gold sequences, simulation is established in asynchronous parallel combinatory spread spectrum system. The results show that Gold sequences self-synchronization of parallel combinatory spread spectrum system can be realized.

Gold sequence; correlation properties; parallel combinatory spread spectrum system; sequence synchronization

TN914.42

A

1002-0802(2016)-07-0826-05

10.3969/j.issn.1002-0802.2016.07.006

2016-03-21;

2016-06-22 Received date:2016-03-21;Revised date:2016-06-22

張 野（1980—），男，碩士，工程師，主要研究方向為通信與信息系統(tǒng)、擴頻通信。