基于前饋補償的直升機控制律設計與仿真

劉宇亮+張琳+朱亞芬

摘要： 以某型運輸直升機為研究對象， 根據飛行品質規范ADS-33E的要求， 在增穩控制的基礎上， 設計前饋補償控制律， 以改善系統的操縱性。 通過擬合不同設計節點的前饋控制參數， 實現包線內的調參控制律。 對所設計的系統進行仿真試驗驗證， 結果表明采用上述控制方案可取得良好的控制效果， 證明了該方法的可行性和有效性。

關鍵詞： 直升機； 飛行品質規范； 前饋補償； 控制律； 系統仿真

中圖分類號： V249.122+.4 文獻標識碼： A 文章編號： 1673-5048（2016）04-0030-06

Abstract： Taking a transport helicopter as the research subject， based on stability augmentation control， feedforward compensation control law is designed to improve the control system according to the flying qualities specification of ADS-33E. By fitting the feedforward control parameters of different flight nodes， parameter adjusting control law in the full scale flight envelop can be realized. The designed system is simulated and tested， and the results indicate that satisfied control effect is obtained by adopting the proposed control method， which proves the feasibility and effectiveness of the method.

Key words： helicopter； flying qualities specification； feedforward compensation； control law； system simulation

0引言

由于直升機的穩定性較差， 只靠飛行員操縱來完成復雜、 精確的飛行是非常困難的， 故需要通過加入飛行控制系統來改善其飛行品質[1]。 基于三軸穩定控制的增穩控制系統雖然能夠有效提高飛機的穩定性， 但是會導致系統響應的速度變慢、 幅值變小， 從而造成快捷性、 操縱功效等性能指標等級不高。 針對上述問題， 可以通過在增穩控制回路前面增加一個前饋電氣通道的方式來解決問題， 這就是控制增穩系統， 該系統能夠在兼顧直升機穩定性的同時提高操縱功效等性能。 此外， 直升機各通道之間耦合影響嚴重， 通過前饋補償方式實現交聯解耦控制， 可以有效提高直升機的操縱品質。 所以， 直升機控制增穩系統的設計與實現具有重要的理論意義和實際意義。

1飛行品質規范ADS-33E的要求

針對直升機操縱性能的優劣， 美國軍用直升機飛行品質規范ADS-33E[2-3]有明確規定。

1.1對姿態響應的要求

飛行品質規范ADS-33E分別針對飛機的小幅/高頻、 小幅/中頻、 中幅/中低頻和大幅姿態變化的響應規定了相應的指標要求， 即帶寬及相位滯后、 阻尼比、 快捷性和操縱功效。 對于俯仰姿態變化， 5°以下為小幅， 30°以上為大幅； 滾轉姿態的劃分界限為10°和60°； 對航向角沒有明確數據。 飛行速度V≤23 m/s時為低速和懸停狀態； V>23 m/s時為前飛狀態。

帶寬及相位滯后指標規定了頻域要求， 保證快速操縱時直升機具有良好的跟隨性和靈敏度。 設從駕駛員輸入量到相應姿態角輸出量的傳遞函數為G（s）， 相關定義在其波特圖中， 如圖1所示。

圖1中出現了相位帶寬和增益帶寬， 其中相位滯后135°的頻率定義為相位帶寬， 在幅頻曲線上留出6 dB的余量所對應的頻率為增益帶寬。 由于研究對象的響應類型為姿態指令姿態保持響應類型（ACAH）， 帶寬ωBW=ωBWphase。 延遲時間τp用以表示系統的相位滯后， τp越小說明相位曲線隨頻率下降越慢， 直升機的駕駛品質越好。

飛行品質指標的要求如圖2所示。 為了表征帶寬和延遲時間與飛行品質的關系， ADS-33E在帶寬-延遲時間二維平面內定義了不同的區域， 以區別飛行品質的高低； 而且按照不同的任務科目基元、 環境感知度和控制通道規定了不同的標準。 由于本文的研究對象是運輸型直升機， 所以選擇除空戰外的MTE且UCE=1， 以滾轉通道為例， 帶寬與延遲時間的品質指標要求如圖2（a）所示。

對于直升機的動穩定性， 飛行品質規范對系統的阻尼比、 自然頻率也做出了具體的規定。 以滾轉通道為例， 阻尼比和自然頻率的限制如圖2（b）所示。

針對飛機改變姿態的快慢， 對操作響應的快捷性做出要求， 即角速度峰值對姿態改變量之比要足夠大。 以滾轉通道為例， 快捷性指標的要求如圖2（c）所示； 其中 Δpk和Δmin分別為滾轉角階躍響應的峰值和最小值， ppk為滾轉角速度的最大值。

大機動飛行時， 直升機的響應要具備足夠大的姿態變化（對于姿態指令/姿態保持響應型）或足夠大的角速度（對于速率響應型）， 品質規范規定了其最低限。 以滾轉通道為例， 針對姿態指令響應類型且有限機動的飛機， 1級品質等級的要求為在飛機懸停與低速飛行時， 滾轉角至少達到±15°； 在前飛時， 滾轉角至少達到±25°。

1.2對總距操縱響應的要求

航空兵器2016年第4期劉宇亮等： 基于前饋補償的直升機控制律設計與仿真飛行品質規范對總距操縱響應的時域要求為駕駛員對總距桿施加階躍操縱后， 法向速度應在5 s之內具有大致為一階的形狀。 這是為了保證總距突變后初期的法向速度應直線變化， 便于駕駛員精確控制升降和高度。 此外， 品質規范規定了總距操縱的操縱功效， 即操縱總距桿快速偏離配平位置后的1.5 s內， 產生的法向速度至少達到0.81 m/s （等級1）、 0.28 m/s（等級2）、 0.20 m/s（等級3）。

1.3對軸間耦合的要求

式中： A∈R9×9為狀態矩陣， B∈R9×4為控制矩陣， A， B中的參數隨飛行高度和速度的變化而變化； C∈R9×9為輸出矩陣（取為單位陣）； X=[u v w θ ψ q p r]為狀態向量， 其中， u， v， w分別為前向、 橫向和法向速度； θ， ， ψ分別為俯仰角、 滾轉角和航向角； q， p， r分別為直升機繞機體OX， OY， OZ軸的角速度； U=[δeδaδrδc]為輸入向量， 各分量依次為縱向周期變距、 橫向周期變距、 尾槳槳距和總距。

直升機模型中的參數隨飛行高度和速度而變化， 故選取不同高度和速度下的14個飛行狀態點作為研究對象， 如表1所示。

2.2增穩控制系統

為提高直升機的靜穩定性， 便于駕駛員操縱， 通常采用加入增穩控制系統的方法。 本飛機的增穩控制包括三軸穩定和高度穩定兩部分。[4]

三軸穩定控制系統設計的目的是實現直升機姿態角穩定。 在俯仰、 傾斜、 航向三通道分別引入各通道姿態角和姿態角速度信號， 實現比例加測速反饋控制[5]， 并設計滿足要求的控制參數。 高度通道則引入高度傳感器和法向加速度計信號， 設計PID控制器， 保證飛機高度穩定并能跟蹤給定的高度指令[6]。 在增穩系統基礎上設計前饋控制器， 提高飛機的操縱性能。

3增穩控制系統性能的檢驗

依據飛行品質的要求， 通過仿真試驗評價加入增穩系統后飛機的操縱性能， 為前饋控制器的設計提供依據。

3.1對姿態響應的檢驗

取飛行狀態點4（速度V=41 m/s、 高度H=100 m）， 以滾轉通道為例進行檢驗。

使用MATLAB中的linmod（）函數， 求出仿真模型中駕駛桿橫向位移量到滾轉角的傳遞函數； 并根據飛行品質規范中的規定， 計算得出帶寬ωBW=5和延遲時間τp=0.05。 可以看出， 飛機滾轉通道的帶寬與延遲時間達到1級品質指標的要求， 表明前期所設計的三軸穩定控制律達到了較理想的帶寬和延遲時間指標要求。

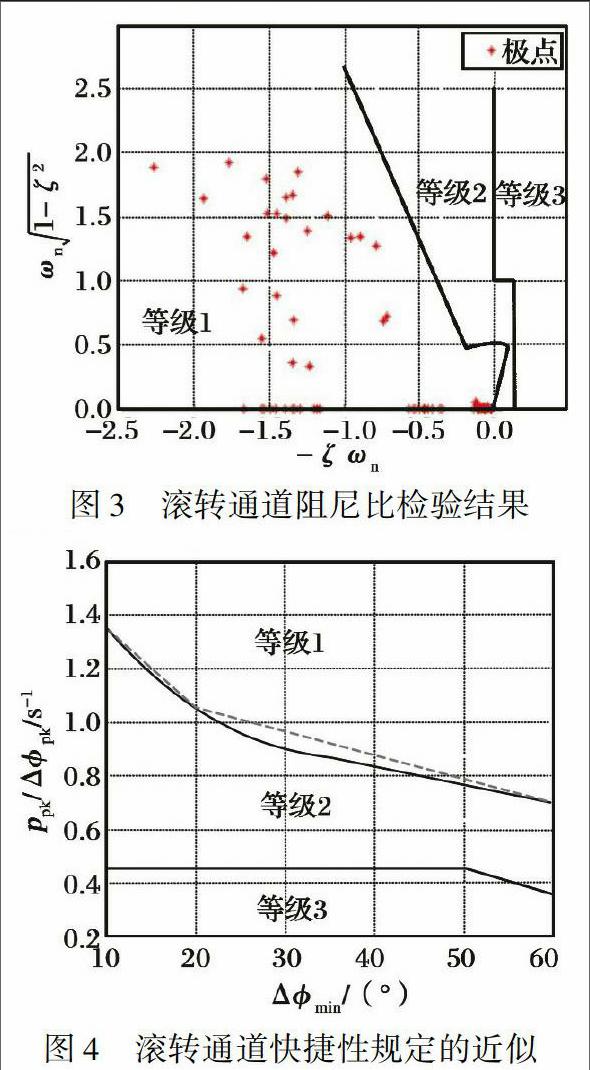
求出駕駛桿位移量到滾轉角傳遞函數的極點， 根據極點在復平面上的位置， 確定阻尼比的品質等級， 見圖3所示。

由圖3可以看出， 滾轉通道傳遞函數的極點全部落在1級品質要求的區域內， 表明加入三軸穩定控制律的飛機具有滿意的阻尼特性。

給直升機的滾轉通道加入幅值為20的階躍信號， 根據仿真試驗得出ppk/Δpk=1.07， 由于階躍響應沒有超調量， 故Δpk=Δmin=12.12， 快捷性和操縱功效都位于2級指標范圍內。 可見加入增穩控制系統后， 飛機的快捷性和操縱功效有待改進。

3.2對總距操縱響應的檢驗

在飛機的高度通道加入幅值為20的階躍信號， 根據仿真結果可知， 14個飛行狀態點下飛機的法向速度變化基本為一階形狀， 1.5 s末的法向速度最小為0.89 m/s， 都能達到1級品質的要求。

3.3對軸間耦合的檢驗

取飛行狀態點4， 首先在高度通道加入幅值為10的階躍輸入， 根據仿真結果得出|r1/w（3）|=0.71， r3/|w（3）|=-0.63， 可知該耦合效應達到等級2。 同理可知， 俯仰-滾轉通道也存在一定的耦合效應， 有必要針對上述2個通道設計解耦控制器。

4控制律設計

由第3節中的仿真驗證及分析可知， 飛機滾轉通道的帶寬與延遲時間、 阻尼比和總距操縱品質指標都達到1級品質； 快捷性、 操縱功效和軸間耦合品質指標有待提高。 本節中， 使用按輸入補償的前饋校正方法， 在飛機原有機械通道的基礎上加入前饋電氣通道， 提高飛機的快捷性和操縱功效； 使用按擾動補償的前饋校正方法， 在飛機的俯仰和高度通道中引出解耦通道， 抑制軸間耦合。

4.1增控通道的設計

根據傳遞函數G（s）的頻域特性可知， 低頻時幅值大且相位滯后小， 高頻時相反， 這樣的特性正好體現了飛行品質規定對不同姿態變化響應的具體要求。

4.1.1參數k的設計

（1） 根據快捷性要求設計參數

快捷性1級品質的要求如圖4所示， 為了方便設計， 把劃分等級的曲線近似為分段直線， 如圖4中虛線所示。

分別在原有機械通道和新加入的前饋電氣通道輸入幅值為20的階躍信號， 通過仿真試驗得出： 經過機械通道， 飛機滾轉角響應的最大值為pk1、 最小值為min1， 最大滾轉角速度為ppk1； 當前饋通道的增益為1時， 滾轉角的最大值為pk2、 最小值為min2， 最大滾轉角速度為ppk2。

式中： k0， k和T均為正數， 由于k0Tk0+k

4.2解耦通道的設計

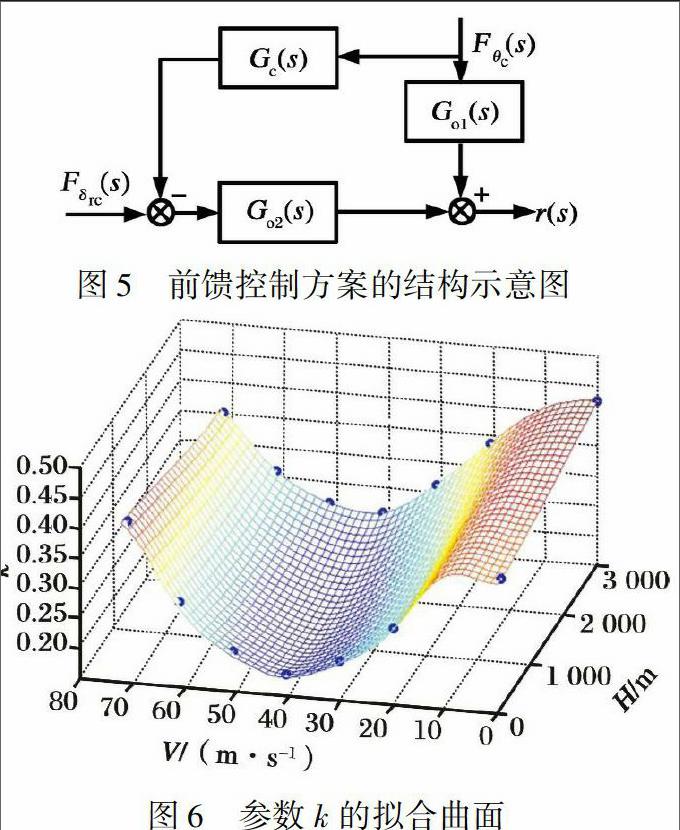
解耦控制系統的工作原理為當駕駛員操縱飛機引起期望之外的響應時， 可以把操縱量看作期望外響應的干擾輸入， 設計該操縱量到期望外響應對應操縱輸入的前饋通道， 用來抵消該操縱量引起的期望外響應。 以高度到航向通道的解耦控制器設計為例， 相應方案的示意圖如圖5所示。

取飛行狀態點4， 針對增穩后的飛機模型， 使用MATLAB中的linmod（）函數， 計算出傳遞函數Go1（s）和Go2（s）， 經過化簡后， 可得高度到航向通道解耦控制器的傳遞函數Gc（s）。

經過仿真可得， 加入解耦控制器后， 飛行員對總距桿輸入相同幅度的階躍量時， |r1/w（3）|的值從0.71減小為0.21； r3/|w（3）|的值從-0.63變為-0.14， 且品質等級達到1級。 由此可得， 解耦控制器Gc（s）可以有效抑制高度到航向通道的交聯耦合。 同理， 可以設計出俯仰到滾轉的解耦控制器。

4.3全包線控制律實現

針對不同飛行狀態點（具體描述見表1）， 分別設計控制器； 并以其參數為樣本， 按照嚴格徑向基神經網絡的算法[7-8]， 使用newrbe（）函數分別得到前饋控制器和解耦控制器傳遞函數參數的神經網絡擬合曲面（其中， 解耦控制器可以整理為尾1標準型， 即分子、 分母各次項系數和開環增益k）。

以開環增益k為例， 其擬合曲面如圖6所示。 可以看出擬合曲面連續、 光滑， 較好地反映了k在包線內的變化趨勢。 相比之下， 速度變化對k的影響較大， 高度變化對k的影響較小， 客觀反映了速度對直升機特性影響較大的事實。

5仿真驗證

以滾轉通道為例檢驗飛機姿態響應的品質等級。 分別對表1中所有飛行狀態點對應的模型進行仿真， 驗證加入控制增穩系統后直升機的動態響應， 以及各飛行品質指標所能達到的等級。 由于加入前饋環節不改變控制系統的極點， 故不再驗證系統的阻尼比。 由于高度通道沒有加入前饋增控環節， 故總距的響應與3.2節中相同， 不再驗證。

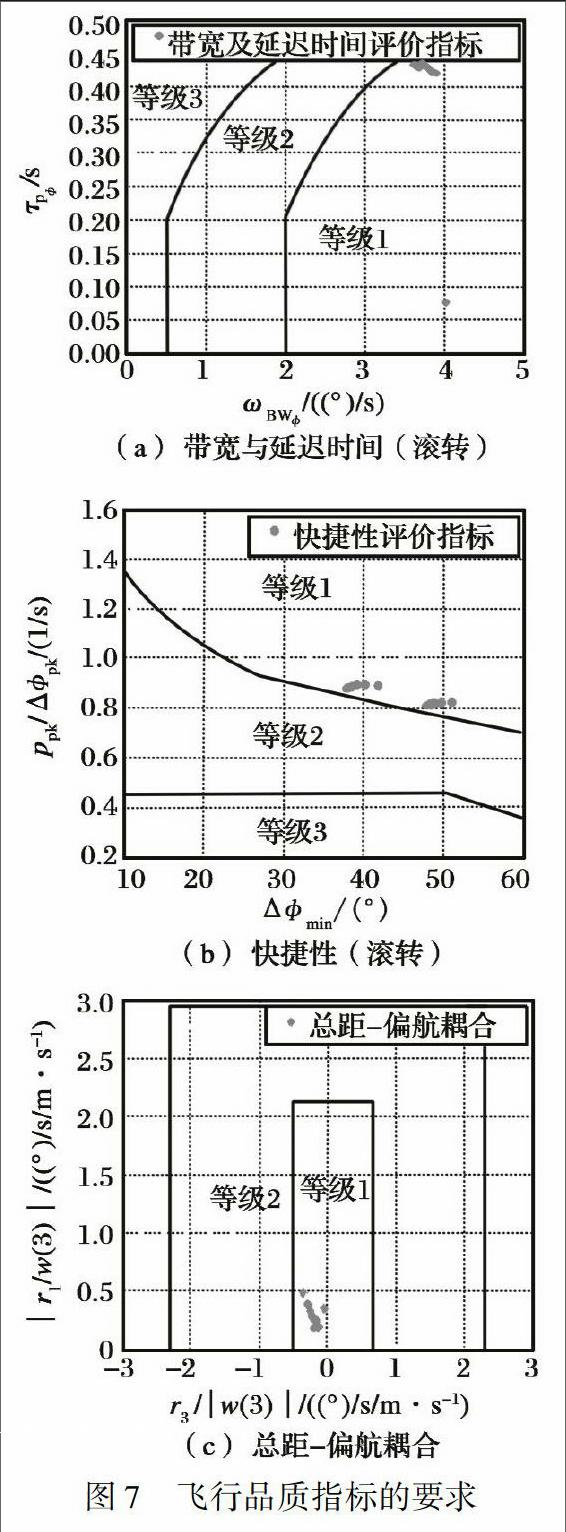
加入前饋增控通道和解耦控制器后， 系統的仿真框圖見圖7。

飛行品質指標的要求如圖7所示。

由圖7（a）可以看出， 飛機的帶寬與延遲時間雖然能夠達到1級品質， 但是， 加入前饋通道后帶寬變窄， 延遲時間變長。 對比飛行狀態4對應的數據發現帶寬ωBW從5變為3.68； 延遲時間τp從0.05變為0.44。 圖7（b）反映出快捷性指標可以達到1級品質， 飛行狀態點5對應的具體數據為ppk/Δpk=0.89， Δpk=Δmin=39.26， 同時Δmin>25說明操縱功效滿足了1級品質的要求。 圖7（c）給出了總距到航向通道軸間耦合的檢驗結果， 可以看出在全部飛行狀態點處， 該指標都滿足1級品質指標的要求。

6結論

針對已實現增穩控制的直升機模型， 本文按照飛行品質規范ADS-33E中的有關規定， 評價了品質指標的等級。 由于飛機的快捷性和操縱功效沒有達到1級品質， 故基于按輸入補償的前饋控制原理， 設計出增控環節； 針對飛機軸間耦合嚴重、 品質等級指標較低的實際情況， 基于按擾動補償的前饋控制原理， 設計出解耦控制器。 經過仿真驗證和數據對比可以看出， 加入增控環節和解耦控制器后， 飛機的快捷性、 操縱功效顯著提高， 軸間耦合明顯減輕， 所考核檢查的指標均可以達到1級標準， 仿真結果證明所采用的控制增穩方法可以達到較好的控制效果。

參考文獻：

[1] 楊一棟. 直升機飛行控制[M].北京： 國防工業出版社， 2007： 25-30.

[2] ADS33E， Handling Qualities Requirements for Military Rotorcrafts[S].United States Army Aviation and Troop Command， 1996.

[3] 榮裊錄.直升機飛行品質設計方法研究[D]. 南京： 南京航空航天大學， 2007.

[4] 趙鵬軒. 直升機過渡懸停及纜位纜高控制律設計與仿真[D].西安： 西北工業大學， 2011.

[5] 凌瓊. 直升機控制律設計[D]. 西安： 西北工業大學， 2008.

[6] 韓旭， 侯明善， 姚成法.基于區間系統的魯棒H∞飛行控制系統設計[J].航空兵器， 2007（3）： 20-24.

[7] 陳龍勝， 姜長生.基于在線神經網絡的無人機著陸飛行自適應逆控制器設計[J].航空兵器， 2009（3）： 22-27.

[8] Hagan M T， Demuth H B， Beale M K. Neural Network Design[M].戴葵， 譯. 北京： 機械工業出版社， 2002.